Getting Started with QuAnTeTrack
Installation
To install the QuAnTeTrack package, we can choose between installing the stable version from CRAN (recommended) or the development version from GitHub.
From CRAN (recommended)
To install the stable version from CRAN, use:
install.packages("QuAnTeTrack")From GitHub (development version)
If we want the latest development version, we will need to use the
devtools package. If we haven’t installed
devtools yet, we can do so with the following command:
install.packages("devtools")Once devtools is installed, we can install
QuAnTeTrack using:
devtools::install_github("MacroFunUV/QuAnTeTrack")If we have already installed QuAnTeTrack and want to ensure we have the latest version, we can update it with:
devtools::install_github("MacroFunUV/QuAnTeTrack", force = TRUE)Terminology
The terminology used throughout QuAnTeTrack follows standardized definitions for tetrapod footprint and trackway analysis. All anatomical, ichnological, and trackway-related terms adhere to the nomenclature and definitions proposed in the Glossary of Tetrapod Tracks published by Lallensack et al. (2025).
By adopting this reference framework, QuAnTeTrack ensures terminological consistency with current ichnological standards and facilitates comparability across studies. Users are encouraged to consult the glossary for detailed definitions.
Overview of the Analytical Workflow in QuAnTeTrack
The QuAnTeTrack package (Quantitative Analysis of Tetrapod Trackways) provides a structured and comprehensive workflow for analyzing trackway data, facilitating the assessment of paleoecological and paleoethological hypotheses. The workflow integrates functions for loading data, observer and anatomical error quantification, exploratory analysis, statistical testing, simulation, similarity assessment, intersection detection, and clustering. This pipeline aims to help researchers reconstruct, compare, and interpret movement patterns and behavioral dynamics of trackmakers.
1. Input Data
1.1 Data Digitization and Preprocessing
The first step involves digitizing the trackway using the TPS software suite, particularly:
-
tpsUtil (Rohlf, 2008): For compiling and
converting
.TPSfiles.
- tpsDig (Rohlf, 2009): For digitizing footprint coordinates from trackways.
The digitization process should ensure that the footprints are consistently recorded across all footprints. This process is essential for converting raw images into structured data for further analysis.
**1.2 Loading Data
Once digitized, the data is loaded into QuAnTeTrack
using the tps_to_track() function. This function:
- Reads
.TPSfiles containing digitized footprints within trackways. - Extracts and organizes data into structured
trackwayR objects. - Handles missing footprints through interpolation if required.
- Converts raw data into real-world measurements using user-specified scales.
The resulting trackway R objects
contain: - Trajectories: A list of trajectories
(trackway midlines interpolated by connecting the midpoints of
successive left–right footprint pairs, i.e., footprints linked by pace
lines). Includes columns X, Y, IMAGE, ID, and Side (set to
“Medial”).
- Footprints: A list of data frames containing
footprint coordinates and metadata, with a Side column (“R” or “L”) and
a missing marker (“Actual” or “Inferred”).
If the dataset is extensive, users can utilize the
subset_track() function to isolate
specific trackways for focused analysis.
1.3 Visual Check and Quantification of Potential Sampling Biases
Before downstream analyses, QuAnTeTrack provides dedicated tools visualize the digitized data and to quantify uncertainty arising from the human sampling process and anatomical fidelity.
Visual Inspection of Trackways (
plot_track()):
Generates visualizations of trackways and footprints to inspect their overall structure.Observer-related uncertainty (
observer_error_partitioning()):
Partitions the variance of trackway parameters into components attributable to biological differences among trackways, inter-observer variability, and intra-observer (replicate) variability using replicated digitizations and mixed-effects models. This analysis allows users to assess reproducibility, identify robust parameters, and evaluate the reliability of measurements prior to hypothesis testing.Anatomical uncertainty (
anatomical_error_partitioning()):
Quantifies the sensitivity of trackway parameters to landmark placement uncertainty using Monte Carlo simulations. By perturbing footprint landmarks within user-defined spatial tolerances, this function estimates the relative contribution of anatomical or taphonomic uncertainty versus genuine biological signal.
Together, these tools enable an explicit audit of data quality and help determine which metrics are robust enough for further interpretation.
2. Descriptive and Kinematic Information
2.1 Exploratory Analysis of Trackway Parameters
Before testing specific hypotheses, users should also perform an initial exploration of the data. This includes:
Parameter Calculation (
track_param()):
Calculates essential movement and trackway parameters, including turning angles; step, stride, and pace lengths; path and beeline lengths; sinuosity and straightness; and footprint-based metrics such as trackway width, gauge, pace angulation, and step angle.Velocity Calculation (
velocity_track()):
Estimates velocities and relative stride lengths for each trackway based on empirical formulations.Visualization of Velocity Patterns (
plot_velocity()):
Examines how velocity or relative stride length varies along each trackway.Direction Analysis (
plot_direction()):
Provides multiple visualization options (boxplots, polar histograms, faceted plots) to explore trackway directionality.
These tools allow users to identify general patterns, trends, and potential anomalies prior to formal statistical analyses.
2.2 Testing Directional and Velocity Patterns
To assess whether trackways exhibit distinct estimated velocities and movement patterns (i.e., trackway orientation patterns), the following statistical tests can be applied:
Testing Velocity (
test_velocity()):
Compares mean velocities across trackways using ANOVA, Kruskal–Wallis, or GLM approaches.Movement Mode Analysis (
mode_velocity()):
Uses Spearman’s rank correlation to detect acceleration, deceleration, or steady movement along trackways.Testing Direction (
test_direction()):
Compares mean directions across trackways using a suit of circular statistical tests.
3. Testing (Paleo)Ethological Hypotheses
QuAnTeTrack tests paleoecological and paleoethological hypotheses by comparing observed fossil trackways with null expectations generated from simulated, independent movement. Under coordinated or sequential movement (e.g., pursuit, queuing or herding), trajectories are expected to show higher covariation and characteristic intersection patterns than predicted by chance. QuAnTeTrack quantifies these patterns using trajectory similarity metrics and intersection analyses, and evaluates them against Monte Carlo–derived null distributions generated under movement scenarios with different degrees of environmental constraint. This framework allows researchers to distinguish genuine behavioral coordination from patterns imposed by environmental structure.
3.1 Simulation of Null (i.e., Independent) Movement Models
(simulate_track())
The simulate_track() function generates simulated
trajectories under different models that represent different
levels of constraint on movement, while assuming independence
among trackmakers. These models define alternative null scenarios
against which observed trackways are evaluated (Directed
model, Constrained model, and
Unconstrained model). Simulations can be visually
compared with empirical trackways using plot_sim().
3.2 Comparing Simulated and Empirical Trackways
Similarity and interactions among trackways are calculated using:
- Dynamic Time Warping
(
simil_DTW_metric()) - Fréchet distance
(
simil_Frechet_metric()) - Trackway intersections
(
track_intersection())
Observed values are evaluated against distributions generated under simulated null models to estimate the statistical support for coordinated versus independent movement.
3.3 Combining Probability Metrics
(combined_prob())
The combined_prob() function integrates
p-values from multiple metrics (i.e., Dynamic Time Warping,
Fréchet distance, and intersection counts) into a single global
probability, providing a more robust statistical assessment of
paleoethological hypotheses about trackmakers movement.
3.4 Clustering Analysis
(cluster_track())
The cluster_track() function groups trackways based on
movement parameters and can be applied prior to formal testing to
identify behavioral groupings and guide hypothesis-driven analyses.
Below is a fully rewritten and expanded “Raw Data Format” section, developed in the same format and style as our original, but with all steps, assumptions, and implications made explicit. Nothing is left implicit, and the workflow is fully tied together to avoid user confusion.
Raw Data Format
QuAnTeTrack accepts raw data in the form of
.TPS files containing 2D footprint
coordinates, organized by trackways.
What is a TPS file in this context?
A TPS file is a plain-text format widely used in geometric morphometrics to store landmark coordinates associated with images. In QuAnTeTrack, TPS files are used in a trackway-centric way, where:
- Each trackway is treated as one specimen
- Each specimen consists of multiple landmarks
- Each landmark corresponds to one footprint reference point
- Landmark order reflects the temporal sequence of footprint formation, from earliest to latest along the trackway
General Requirements
Footprint coordinates must be digitized using equivalent reference points within each footprint (see Landmarking tips below).
-
Trackways with missing footprints are acceptable. Missing footprints may be:
- Truly absent (not preserved), or
- Present but lacking sufficient anatomical fidelity to identify the
chosen reference point These will be interpolated, if
specified, by the function
tps_to_track().
-
All digitization should be performed using the TPS software suite, specifically:
- tpsUtil (Rohlf, 2008) — for file creation, image handling, and TPS file management.
- tpsDig (Rohlf, 2009) — for interactive digitization of landmarks.
Shared map / orthophoto concept and digitization workflow
Definition: shared map or orthophoto
A shared map or orthophoto of the tracksite surface is a single, fixed background image representing the entire footprint-bearing surface, used as the common spatial reference for all digitized trackways from a site.
This image may be:
- A true orthophoto generated via photogrammetry or laser scanning (preferred), or
- A scaled site map or plan-view raster (acceptable if spatially accurate)
The essential requirement is that all trackways are digitized in the same coordinate system, derived from this single image.
Explicit digitization workflow
-
Image capture
- Obtain one shared image (orthophoto or scaled map) of the complete tracksite surface.
-
TPS file preparation (tpsUtil)
Replicate this image as many times as the number of trackways to be digitized.
-
Use tpsUtil → “Build TPS file from images” to generate a
.TPSfile containing:- Multiple identical images
- One image slot per trackway
At this stage, the TPS file contains no landmarks.
-
Landmark digitization (tpsDig)
Open the TPS file in tpsDig.
-
For each replicated image:
- Digitize only one trackway
- Enter landmarks sequentially following the timeline of movement, from the earliest formed footprint to the latest
Move to the next image and repeat for the next trackway.
This workflow uses the same image copied repeatedly, with only one trackway digitized per image. This ensures that all trackways share a common spatial reference while remaining independent specimens.
Image capture and spatial biases
Potential sources of bias
Digital recording methods (photography, photogrammetry, laser scanning) introduce inherent biases that propagate through the entire analytical pipeline:
- Optical distortion (lens curvature, oblique angles) alters footprint geometry.
- Uneven resolution or shadows may obscure anatomical features.
- Scale-bar misplacement (tilted or not coplanar with the surface) biases all distance-based metrics, including step length, velocity proxies, and sinuosity.
- Even small scaling errors systematically affect all derived parameters.
Georeferencing and orientation
When digitizing trackways from images or slabs:
Orientation relative to external references (e.g., north, bedding planes, slope) must be explicitly defined.
-
Misalignment alters:
- Calculated movement directions
- Turning angles
- Comparability among trackways
Inconsistent reference systems invalidate cross-trackway comparisons.
Orthogonal photographs are strongly recommended. Tracksites with abrupt slopes or complex topographies may be misleading when represented in 2D until a future 3D implementation of QuAnTeTrack becomes available.
Best practices to minimize bias
- Prefer high-resolution, calibrated methods (controlled photography, photogrammetry, laser scanning).
- Ensure image resolution exceeds the scale fidelity of the smallest footprint features.
- Place scale bars coplanar with the track surface and clearly visible.
- Correct optical distortion and avoid oblique imaging angles.
- Regularly verify scale using known distances on the slab.
- Establish orientation relative to external references (north, bedding, slope).
Landmarking tips
Choice of reference point
Footprint coordinates must be digitized at a consistently identifiable reference point within each footprint, such as:
- Tips of digit impressions
- Centroids of phalangeal pads
- Track centroids (for morphologically simple tracks)
Reference points are mathematically expressed as 2D (or future 3D) coordinates.
Footprint landmarks do not always represent strictly homologous
anatomical features. Variations in claw mark position, pad definition,
or digit orientation often reflect foot kinematics and
behavior, rather than anatomy. The impact of this uncertainty
can be explicitly evaluated using the
anatomical_error_partitioning() function.
Track-type–specific conventions
Trackway parameters require a reference point that is identifiable across all measurable footprints:
- Amphibians and reptiles: base of digit impression III
- Tridactyl tracks: tip of digit impression III
- Sauropod tracks or poorly defined tracks: track centroid
- Hominin tracks: pternion of the heel
Distal reference points (e.g., digit tips) are more sensitive to foot rotation and kinematic variability, which may increase variance in derived parameters.
Missing and ambiguous footprints
Trackways with missing footprints are acceptable.
Interpolation may be applied using
tps_to_track()when specified.-
This applies both to:
- Truly absent footprints
- Present footprints lacking sufficient anatomical fidelity to locate the chosen reference point
Pes vs. manus digitization
It is strongly recommended to digitize pes trackways only, except in cases where manus trackways are the explicit focus of the study. Several downstream calculations in the QuAnTeTrack workflow assume pes-based measurements.
For further discussion of footprint reference points and landmarking strategies, see Lallensack et al. (2025) and Zelditsh et al. (2012), and references therein.
This vignette demonstrates how to load, process, and analyze
trackway data using the QuAnTeTrack package.
We will walk through the Paluxy River and the
Mount Tom datasets, representing dinosaur trackways
from the Paluxy River site (Farlow et al., 2012) and the Mount
Tom site (Ostrom, 1972), respectively. Examples of
.tps files of these datasets can be downloaded here:
Loading and Converting Data
The tps_to_track() function is an
essential component of the QuAnTeTrack package,
designed to transform raw .TPS files
containing digitized trackway data into structured
trackway R objects. This tool is
particularly useful for reconstructing trackway midlines (i.e.,
trajectories) from footprints digitized using the TPS software
suite. The function reads the raw .TPS
files, extracts the coordinate data, and processes it to
generate trackway R objects that are
compatible with the analytical tools provided by
QuAnTeTrack.
The tps_to_track() function reads
.TPS files where each trackway is
represented by a series of (x, y) coordinates (i.e.,
reference points of footprints) stored as separate images. These data
points are then processed to generate trackway midline
coordinates by interpolating the midpoints of
successive pace lines.
These trackway midline coordinates serve as reconstructed trajectories, allowing users to analyze overall movement patterns. When missing footprints are encountered, the function can interpolate their positions based on the locations of adjacent footprints and the specified laterality (left or right) of the initial footprint.
Several arguments are provided to customize data handling. The
file argument specifies the path to the
.TPS file, while the scale
argument allows users to define a scale factor (in meters per
pixel) to convert coordinates to real-world measurements. To
account for missing footprints, the
missing argument specifies whether
interpolation is required, while the NAs
argument provides a matrix detailing which footprints need
interpolation. Additionally, the R.L.side
argument identifies whether the first footprint of each trackway belongs
to the left or right side, which is essential when
dealing with incomplete trackways.
The function generates a trackway R
object consisting of two main components:
Trajectories and
Footprints. The
Trajectories element contains a list of
interpolated trajectories, where each trajectory represents a series of
midpoints between successive left–right footprint pairs. The
Footprints element comprises a list of
data frames with the original footprint coordinates, associated metadata
(such as image reference and ID), and an indicator specifying whether
each footprint is actual or inferred.
The resulting trackway R object
provides a comprehensive framework for organizing digitized trackway
data, making it compatible with the various analytical functions within
the QuAnTeTrack package. By transforming raw data into
structured objects, the tps_to_track()
function serves as a foundational step in the broader analytical
pipeline provided by QuAnTeTrack.
Examples of Usage
Here, the TPS files (PaluxyRiver.tps and
MountTom.tps) are loaded using the
system.file() function to ensure compatibility across
systems. This approach is necessary because these files are stored as
internal data within the package (specifically, in the
inst/extdata/ folder). Using system.file()
ensures that the files can be accessed regardless of the user’s
operating system or working directory, making the vignette fully
portable and reproducible. They are then converted to
trackway R objects using the tps_to_track()
function. For the PaluxyRiver dataset, no footprints
are missing, so the missing argument is set to
FALSE and NAs = NULL. For the
MountTom dataset, some footprints are missing, so the
missing argument is set to TRUE, and the
missing footprints are specified using the NAs matrix.
Additionally, the R.L.side argument is provided to specify
the laterality of the first footprint of each trackway.
For users working with their own data, replace
system.file("extdata", "PaluxyRiver.tps", package = "QuAnTeTrack")
and
system.file("extdata", "MountTom.tps", package = "QuAnTeTrack")
with the file paths to our .TPS files (e.g.,
"C:/path/to/our/PaluxyRiver.tps" and
"C:/path/to/our/MountTom.tps").
PaluxyRiver <- tps_to_track(
system.file("extdata", "PaluxyRiver.tps", package = "QuAnTeTrack"),
scale = 0.004,
R.L.side = c("R", "L"),
missing = FALSE,
NAs = NULL
)
MountTom <- tps_to_track(
system.file("extdata", "MountTom.tps", package = "QuAnTeTrack"),
scale = 0.004,
missing = TRUE,
NAs = matrix(c(7, 3), nrow = 1, ncol = 2),
R.L.side = c(
"R", "L", "L", "L", "R", "L", "R", "R", "L", "L", "L", "L", "L",
"R", "R", "L", "R", "R", "L", "R", "R", "R", "R"
)
)Subsetting trackways from trackway Data
The subset_track() function is designed
to extract specific trackways from a larger dataset of trackways, making
it easier to focus on particular trajectories or
footprints for further analysis or visualization. This function
is particularly useful when working with extensive
datasets where only a subset of trackways is relevant to the
research question.
The function operates by taking a trackway R
object, which contains two elements:
Trajectories and
Footprints. Each of these elements is a
list, where each list entry corresponds to a separate
trackway. By specifying the desired indices through the
tracks argument, users can isolate
particular trackways of interest.
If the tracks argument is left
unspecified (NULL), the function defaults
to returning all trackways in the dataset. Otherwise,
it subsets the dataset based on the indices provided.
If any indices are outside the range of available
trackways, they are ignored with a warning
message to notify the user. This functionality ensures
robustness when working with datasets of varying sizes.
The function returns a modified trackway R
object with the same structure as the original, but only
containing the specified trackways. This approach maintains
compatibility with other functions that expect a
trackway R object, allowing for seamless
integration into broader analytical workflows.
Examples of Usage
To prepare a subset of trackways with more than three
footprints from the MountTom dataset for later
analyses, we can use the subset_track()
function. This is especially useful for focusing on a selection of
trackways of interest before applying similarity metrics, simulations,
or statistical tests.
sbMountTom <- subset_track(MountTom, tracks = c(1, 2, 3, 4, 7, 8, 9, 13, 15, 16, 18))
print(sbMountTom)#> $Trajectories
#> $Trajectories$Trackway_01
#> x y IMAGE ID Side time displacementTime polar
#> 1 36.882 14.056 Track 1.png 0 Medial 0.00 0.00 36.882+14.056i
#> 2 36.190 14.738 Track 1.png 0 Medial 0.02 0.02 36.190+14.738i
#> 3 35.552 15.378 Track 1.png 0 Medial 0.04 0.04 35.552+15.378i
#> 4 34.862 15.974 Track 1.png 0 Medial 0.06 0.06 34.862+15.974i
#> 5 34.234 16.620 Track 1.png 0 Medial 0.08 0.08 34.234+16.620i
#> 6 33.682 17.314 Track 1.png 0 Medial 0.10 0.10 33.682+17.314i
#> 7 33.036 17.860 Track 1.png 0 Medial 0.12 0.12 33.036+17.860i
#> 8 32.410 18.324 Track 1.png 0 Medial 0.14 0.14 32.410+18.324i
#> 9 31.764 18.926 Track 1.png 0 Medial 0.16 0.16 31.764+18.926i
#> displacement
#> 1 0.000+0.000i
#> 2 -0.692+0.682i
#> 3 -0.638+0.640i
#> 4 -0.690+0.596i
#> 5 -0.628+0.646i
#> 6 -0.552+0.694i
#> 7 -0.646+0.546i
#> 8 -0.626+0.464i
#> 9 -0.646+0.602i
#>
#> $Trajectories$Trackway_02
#> x y IMAGE ID Side time displacementTime polar
#> 1 35.532 13.516 Track 2.png 1 Medial 0.00 0.00 35.532+13.516i
#> 2 34.966 14.124 Track 2.png 1 Medial 0.02 0.02 34.966+14.124i
#> 3 34.328 14.770 Track 2.png 1 Medial 0.04 0.04 34.328+14.770i
#> 4 33.658 15.454 Track 2.png 1 Medial 0.06 0.06 33.658+15.454i
#> 5 33.062 16.230 Track 2.png 1 Medial 0.08 0.08 33.062+16.230i
#> 6 32.486 17.170 Track 2.png 1 Medial 0.10 0.10 32.486+17.170i
#> 7 31.952 17.986 Track 2.png 1 Medial 0.12 0.12 31.952+17.986i
#> 8 31.356 18.664 Track 2.png 1 Medial 0.14 0.14 31.356+18.664i
#> 9 30.786 19.460 Track 2.png 1 Medial 0.16 0.16 30.786+19.460i
#> displacement
#> 1 0.000+0.000i
#> 2 -0.566+0.608i
#> 3 -0.638+0.646i
#> 4 -0.670+0.684i
#> 5 -0.596+0.776i
#> 6 -0.576+0.940i
#> 7 -0.534+0.816i
#> 8 -0.596+0.678i
#> 9 -0.570+0.796i
#>
#> $Trajectories$Trackway_03
#> x y IMAGE ID Side time displacementTime polar
#> 1 34.548 14.100 Track 3.png 2 Medial 0.00 0.00 34.548+14.100i
#> 2 33.796 14.884 Track 3.png 2 Medial 0.02 0.02 33.796+14.884i
#> 3 32.968 15.748 Track 3.png 2 Medial 0.04 0.04 32.968+15.748i
#> 4 32.146 16.720 Track 3.png 2 Medial 0.06 0.06 32.146+16.720i
#> 5 31.444 17.498 Track 3.png 2 Medial 0.08 0.08 31.444+17.498i
#> displacement
#> 1 0.000+0.000i
#> 2 -0.752+0.784i
#> 3 -0.828+0.864i
#> 4 -0.822+0.972i
#> 5 -0.702+0.778i
#>
#> $Trajectories$Trackway_04
#> x y IMAGE ID Side time displacementTime polar
#> 1 32.260 14.518 Track 4.png 3 Medial 0.00 0.00 32.260+14.518i
#> 2 31.608 15.416 Track 4.png 3 Medial 0.02 0.02 31.608+15.416i
#> 3 31.074 16.300 Track 4.png 3 Medial 0.04 0.04 31.074+16.300i
#> 4 30.528 17.076 Track 4.png 3 Medial 0.06 0.06 30.528+17.076i
#> 5 29.846 17.804 Track 4.png 3 Medial 0.08 0.08 29.846+17.804i
#> displacement
#> 1 0.000+0.000i
#> 2 -0.652+0.898i
#> 3 -0.534+0.884i
#> 4 -0.546+0.776i
#> 5 -0.682+0.728i
#>
#> $Trajectories$Trackway_07
#> x y IMAGE ID Side time displacementTime
#> 1 28.29000 13.57800 Track 7.png 6 Medial 0.00 0.00
#> 2 28.06771 14.30693 Track 7.png 6 Medial 0.02 0.02
#> 3 27.84771 14.91693 Track 7.png 6 Medial 0.04 0.04
#> 4 27.42400 15.54200 Track 7.png 6 Medial 0.06 0.06
#> 5 26.91000 16.31200 Track 7.png 6 Medial 0.08 0.08
#> 6 26.34600 17.05800 Track 7.png 6 Medial 0.10 0.10
#> 7 25.84400 17.73600 Track 7.png 6 Medial 0.12 0.12
#> polar displacement
#> 1 28.29000+13.57800i 0.0000000+0.0000000i
#> 2 28.06771+14.30693i -0.2222901+0.7289282i
#> 3 27.84771+14.91693i -0.2200000+0.6100000i
#> 4 27.42400+15.54200i -0.4237099+0.6250718i
#> 5 26.91000+16.31200i -0.5140000+0.7700000i
#> 6 26.34600+17.05800i -0.5640000+0.7460000i
#> 7 25.84400+17.73600i -0.5020000+0.6780000i
#>
#> $Trajectories$Trackway_08
#> x y IMAGE ID Side time displacementTime polar
#> 1 26.198 13.698 Track 8.png 7 Medial 0.00 0.00 26.198+13.698i
#> 2 25.532 14.608 Track 8.png 7 Medial 0.02 0.02 25.532+14.608i
#> 3 24.960 15.572 Track 8.png 7 Medial 0.04 0.04 24.960+15.572i
#> 4 24.484 16.500 Track 8.png 7 Medial 0.06 0.06 24.484+16.500i
#> 5 23.970 17.322 Track 8.png 7 Medial 0.08 0.08 23.970+17.322i
#> 6 23.330 18.274 Track 8.png 7 Medial 0.10 0.10 23.330+18.274i
#> displacement
#> 1 0.000+0.000i
#> 2 -0.666+0.910i
#> 3 -0.572+0.964i
#> 4 -0.476+0.928i
#> 5 -0.514+0.822i
#> 6 -0.640+0.952i
#>
#> $Trajectories$Trackway_09
#> x y IMAGE ID Side time displacementTime polar
#> 1 26.472 15.496 Track 9.png 8 Medial 0.00 0.00 26.472+15.496i
#> 2 27.688 14.882 Track 9.png 8 Medial 0.02 0.02 27.688+14.882i
#> 3 28.904 14.418 Track 9.png 8 Medial 0.04 0.04 28.904+14.418i
#> 4 30.064 13.978 Track 9.png 8 Medial 0.06 0.06 30.064+13.978i
#> 5 31.054 13.640 Track 9.png 8 Medial 0.08 0.08 31.054+13.640i
#> displacement
#> 1 0.000+0.000i
#> 2 1.216-0.614i
#> 3 1.216-0.464i
#> 4 1.160-0.440i
#> 5 0.990-0.338i
#>
#> $Trajectories$Trackway_13
#> x y IMAGE ID Side time displacementTime polar
#> 1 13.218 8.752 Track 13.png 12 Medial 0.00 0.00 13.218+8.752i
#> 2 12.906 8.434 Track 13.png 12 Medial 0.02 0.02 12.906+8.434i
#> 3 12.592 8.170 Track 13.png 12 Medial 0.04 0.04 12.592+8.170i
#> 4 12.358 7.872 Track 13.png 12 Medial 0.06 0.06 12.358+7.872i
#> 5 12.170 7.490 Track 13.png 12 Medial 0.08 0.08 12.170+7.490i
#> displacement
#> 1 0.000+0.000i
#> 2 -0.312-0.318i
#> 3 -0.314-0.264i
#> 4 -0.234-0.298i
#> 5 -0.188-0.382i
#>
#> $Trajectories$Trackway_15
#> x y IMAGE ID Side time displacementTime polar
#> 1 15.638 8.164 Track 15.png 14 Medial 0.00 0.00 15.638+ 8.164i
#> 2 15.244 9.038 Track 15.png 14 Medial 0.02 0.02 15.244+ 9.038i
#> 3 14.850 10.048 Track 15.png 14 Medial 0.04 0.04 14.850+10.048i
#> 4 14.344 10.964 Track 15.png 14 Medial 0.06 0.06 14.344+10.964i
#> 5 13.808 11.868 Track 15.png 14 Medial 0.08 0.08 13.808+11.868i
#> displacement
#> 1 0.000+0.000i
#> 2 -0.394+0.874i
#> 3 -0.394+1.010i
#> 4 -0.506+0.916i
#> 5 -0.536+0.904i
#>
#> $Trajectories$Trackway_16
#> x y IMAGE ID Side time displacementTime polar
#> 1 14.698 6.798 Track 16.png 15 Medial 0.00 0.00 14.698+ 6.798i
#> 2 14.330 7.534 Track 16.png 15 Medial 0.02 0.02 14.330+ 7.534i
#> 3 13.868 8.270 Track 16.png 15 Medial 0.04 0.04 13.868+ 8.270i
#> 4 13.392 9.092 Track 16.png 15 Medial 0.06 0.06 13.392+ 9.092i
#> 5 12.870 9.940 Track 16.png 15 Medial 0.08 0.08 12.870+ 9.940i
#> 6 12.276 10.660 Track 16.png 15 Medial 0.10 0.10 12.276+10.660i
#> 7 11.664 11.400 Track 16.png 15 Medial 0.12 0.12 11.664+11.400i
#> 8 11.008 12.038 Track 16.png 15 Medial 0.14 0.14 11.008+12.038i
#> displacement
#> 1 0.000+0.000i
#> 2 -0.368+0.736i
#> 3 -0.462+0.736i
#> 4 -0.476+0.822i
#> 5 -0.522+0.848i
#> 6 -0.594+0.720i
#> 7 -0.612+0.740i
#> 8 -0.656+0.638i
#>
#> $Trajectories$Trackway_18
#> x y IMAGE ID Side time displacementTime polar
#> 1 12.006 7.316 Track 18.png 17 Medial 0.00 0.00 12.006+ 7.316i
#> 2 11.658 8.402 Track 18.png 17 Medial 0.02 0.02 11.658+ 8.402i
#> 3 11.290 9.410 Track 18.png 17 Medial 0.04 0.04 11.290+ 9.410i
#> 4 10.828 10.460 Track 18.png 17 Medial 0.06 0.06 10.828+10.460i
#> 5 10.484 11.362 Track 18.png 17 Medial 0.08 0.08 10.484+11.362i
#> displacement
#> 1 0.000+0.000i
#> 2 -0.348+1.086i
#> 3 -0.368+1.008i
#> 4 -0.462+1.050i
#> 5 -0.344+0.902i
#>
#>
#> $Footprints
#> $Footprints[[1]]
#> X Y IMAGE ID Side missing
#> 1 37.312 13.764 Track 1.png 0 R Actual
#> 2 36.452 14.348 Track 1.png 0 L Actual
#> 3 35.928 15.128 Track 1.png 0 R Actual
#> 4 35.176 15.628 Track 1.png 0 L Actual
#> 5 34.548 16.320 Track 1.png 0 R Actual
#> 6 33.920 16.920 Track 1.png 0 L Actual
#> 7 33.444 17.708 Track 1.png 0 R Actual
#> 8 32.628 18.012 Track 1.png 0 L Actual
#> 9 32.192 18.636 Track 1.png 0 R Actual
#> 10 31.336 19.216 Track 1.png 0 L Actual
#>
#> $Footprints[[2]]
#> X Y IMAGE ID Side missing
#> 1 35.828 13.196 Track 2.png 1 L Actual
#> 2 35.236 13.836 Track 2.png 1 R Actual
#> 3 34.696 14.412 Track 2.png 1 L Actual
#> 4 33.960 15.128 Track 2.png 1 R Actual
#> 5 33.356 15.780 Track 2.png 1 L Actual
#> 6 32.768 16.680 Track 2.png 1 R Actual
#> 7 32.204 17.660 Track 2.png 1 L Actual
#> 8 31.700 18.312 Track 2.png 1 R Actual
#> 9 31.012 19.016 Track 2.png 1 L Actual
#> 10 30.560 19.904 Track 2.png 1 R Actual
#>
#> $Footprints[[3]]
#> X Y IMAGE ID Side missing
#> 1 34.924 13.648 Track 3.png 2 L Actual
#> 2 34.172 14.552 Track 3.png 2 R Actual
#> 3 33.420 15.216 Track 3.png 2 L Actual
#> 4 32.516 16.280 Track 3.png 2 R Actual
#> 5 31.776 17.160 Track 3.png 2 L Actual
#> 6 31.112 17.836 Track 3.png 2 R Actual
#>
#> $Footprints[[4]]
#> X Y IMAGE ID Side missing
#> 1 32.592 14.072 Track 4.png 3 L Actual
#> 2 31.928 14.964 Track 4.png 3 R Actual
#> 3 31.288 15.868 Track 4.png 3 L Actual
#> 4 30.860 16.732 Track 4.png 3 R Actual
#> 5 30.196 17.420 Track 4.png 3 L Actual
#> 6 29.496 18.188 Track 4.png 3 R Actual
#>
#> $Footprints[[5]]
#> X Y IMAGE ID Side missing
#> 1 28.45200 13.17200 Track 7.png 6 R Actual
#> 2 28.12800 13.98400 Track 7.png 6 L Actual
#> 3 28.00742 14.62986 Track 7.png 6 R Inferred
#> 4 27.68800 15.20400 Track 7.png 6 L Actual
#> 5 27.16000 15.88000 Track 7.png 6 R Actual
#> 6 26.66000 16.74400 Track 7.png 6 L Actual
#> 7 26.03200 17.37200 Track 7.png 6 R Actual
#> 8 25.65600 18.10000 Track 7.png 6 L Actual
#>
#> $Footprints[[6]]
#> X Y IMAGE ID Side missing
#> 1 26.612 13.296 Track 8.png 7 R Actual
#> 2 25.784 14.100 Track 8.png 7 L Actual
#> 3 25.280 15.116 Track 8.png 7 R Actual
#> 4 24.640 16.028 Track 8.png 7 L Actual
#> 5 24.328 16.972 Track 8.png 7 R Actual
#> 6 23.612 17.672 Track 8.png 7 L Actual
#> 7 23.048 18.876 Track 8.png 7 R Actual
#>
#> $Footprints[[7]]
#> X Y IMAGE ID Side missing
#> 1 25.844 15.892 Track 9.png 8 L Actual
#> 2 27.100 15.100 Track 9.png 8 R Actual
#> 3 28.276 14.664 Track 9.png 8 L Actual
#> 4 29.532 14.172 Track 9.png 8 R Actual
#> 5 30.596 13.784 Track 9.png 8 L Actual
#> 6 31.512 13.496 Track 9.png 8 R Actual
#>
#> $Footprints[[8]]
#> X Y IMAGE ID Side missing
#> 1 13.356 8.884 Track 13.png 12 L Actual
#> 2 13.080 8.620 Track 13.png 12 R Actual
#> 3 12.732 8.248 Track 13.png 12 L Actual
#> 4 12.452 8.092 Track 13.png 12 R Actual
#> 5 12.264 7.652 Track 13.png 12 L Actual
#> 6 12.076 7.328 Track 13.png 12 R Actual
#>
#> $Footprints[[9]]
#> X Y IMAGE ID Side missing
#> 1 15.848 7.800 Track 15.png 14 R Actual
#> 2 15.428 8.528 Track 15.png 14 L Actual
#> 3 15.060 9.548 Track 15.png 14 R Actual
#> 4 14.640 10.548 Track 15.png 14 L Actual
#> 5 14.048 11.380 Track 15.png 14 R Actual
#> 6 13.568 12.356 Track 15.png 14 L Actual
#>
#> $Footprints[[10]]
#> X Y IMAGE ID Side missing
#> 1 14.844 6.412 Track 16.png 15 L Actual
#> 2 14.552 7.184 Track 16.png 15 R Actual
#> 3 14.108 7.884 Track 16.png 15 L Actual
#> 4 13.628 8.656 Track 16.png 15 R Actual
#> 5 13.156 9.528 Track 16.png 15 L Actual
#> 6 12.584 10.352 Track 16.png 15 R Actual
#> 7 11.968 10.968 Track 16.png 15 L Actual
#> 8 11.360 11.832 Track 16.png 15 R Actual
#> 9 10.656 12.244 Track 16.png 15 L Actual
#>
#> $Footprints[[11]]
#> X Y IMAGE ID Side missing
#> 1 12.276 6.748 Track 18.png 17 R Actual
#> 2 11.736 7.884 Track 18.png 17 L Actual
#> 3 11.580 8.920 Track 18.png 17 R Actual
#> 4 11.000 9.900 Track 18.png 17 L Actual
#> 5 10.656 11.020 Track 18.png 17 R Actual
#> 6 10.312 11.704 Track 18.png 17 L ActualPlotting trackways
The plot_track() function is a
versatile tool designed to visualize trackway and footprint
data from a trackway R object in
various ways, providing a flexible approach to examining and presenting
trackway datasets. This function generates customizable plots using the
ggplot2 package, allowing users to inspect
individual trajectories, footprints, or a combination of both. By
adjusting various plotting parameters, users can tailor their
visualizations to highlight specific aspects of the dataset, such as
individual trajectories paths, footprint
shapes, and colors, among others.
The plot_track() function allows users
to choose between three plotting modes: plotting only the
footprints, only the interpolated
trajectories, or a combination of both. This
is controlled by the plot argument, which
can be set to "Footprints",
"Trajectories", or
"FootprintsTrajectories" (default). The
footprints and trajectories are plotted using different layers, with
footprints represented by points and trajectories
represented by lines.
The plot_track() function also allows
users to visualize the direction of movement along
trackways by adding arrowheads at the terminal end of each
trajectory. This behavior is controlled by the
arrow.t argument. When
arrow.t = TRUE, arrowheads are drawn at
the end of trajectory lines, indicating the inferred direction of
progression along each trackway. The size of the arrowheads can be
adjusted using the arrow.size argument,
allowing arrows to be scaled appropriately for different plotting
resolutions or figure sizes. Arrow color and transparency are
automatically inherited from the corresponding trajectory lines (i.e.,
they follow the settings of colours and
alpha.t), ensuring visual consistency
between trajectories and their associated directional indicators.
In addition to these options, the
plot_track() function allows users to
inspect the sequence of footprints along each trackway
using the seq.foot argument. When
seq.foot = TRUE, footprints are labeled
with their sequential order along the trackway instead of being plotted
as points, using the same size specified by
cex.f. This option is intended as a
diagnostic tool to verify that footprints are correctly ordered along
each trackway after digitization and preprocessing, facilitating the
detection of ordering errors or inconsistencies in the footprint
sequence.
Additional customization options include changing
colors, sizes,
widths, shapes, and
transparency of the plotted elements. Users can provide
a vector of colors via the colours
argument, which allows elements of different trackways to be plotted in
different colors. The cex.f and
cex.t arguments control the sizes of
footprint points and trajectory lines, respectively. The
shape.f argument allows users to specify
the shapes of footprint points, while the
alpha.f,
alpha.t, and
alpha.l arguments control the transparency
of footprints, trajectory lines, and labels, respectively.
The plot_track() function also supports
the addition of labels to individual trackways. If the
plot.labels argument is set to
TRUE, labels are displayed at the start of
each trackway, with the label text determined by the
labels argument. If labels are not
provided, the function automatically generates labels based on trackway
names in the original TPS file. Users can adjust the label size using
the cex.l argument and control the padding
around the labels with the box.p
argument.
The plot_track() function returns a
ggplot object, which can be further
customized using additional ggplot2
functions. This allows users to enhance their plots with additional
layers, themes, and annotations as needed.
The plot_track() function is designed
as a diagnostic and exploratory tool. Its primary
purpose is to display the raw spatial data (footprint coordinates and
interpolated trajectories) that have been digitized, allowing users to
visually confirm data integrity prior to quantitative analyses. This
includes verifying footprint order, assessing trackway orientation, and
checking the correspondence between interpolated trajectories and the
underlying footprint data.
Importantly, these visualizations are not intended to replace
traditional ichnological representations. Hand-drawn maps and
interpretative outlines often convey morphological, taxonomic, and
contextual information that cannot be captured by raw coordinate plots
alone. Instead, plot_track() provides a
reproducible, data-driven visualization that complements classical
ichnological illustrations and serves primarily as a quality-control and
exploratory aid.
Examples of Usage
By default, plot_track() displays both
footprints and interpolated trajectories. This is useful for getting a
general overview of the track and its corresponding interpolated
pathways.
plot_track(PaluxyRiver)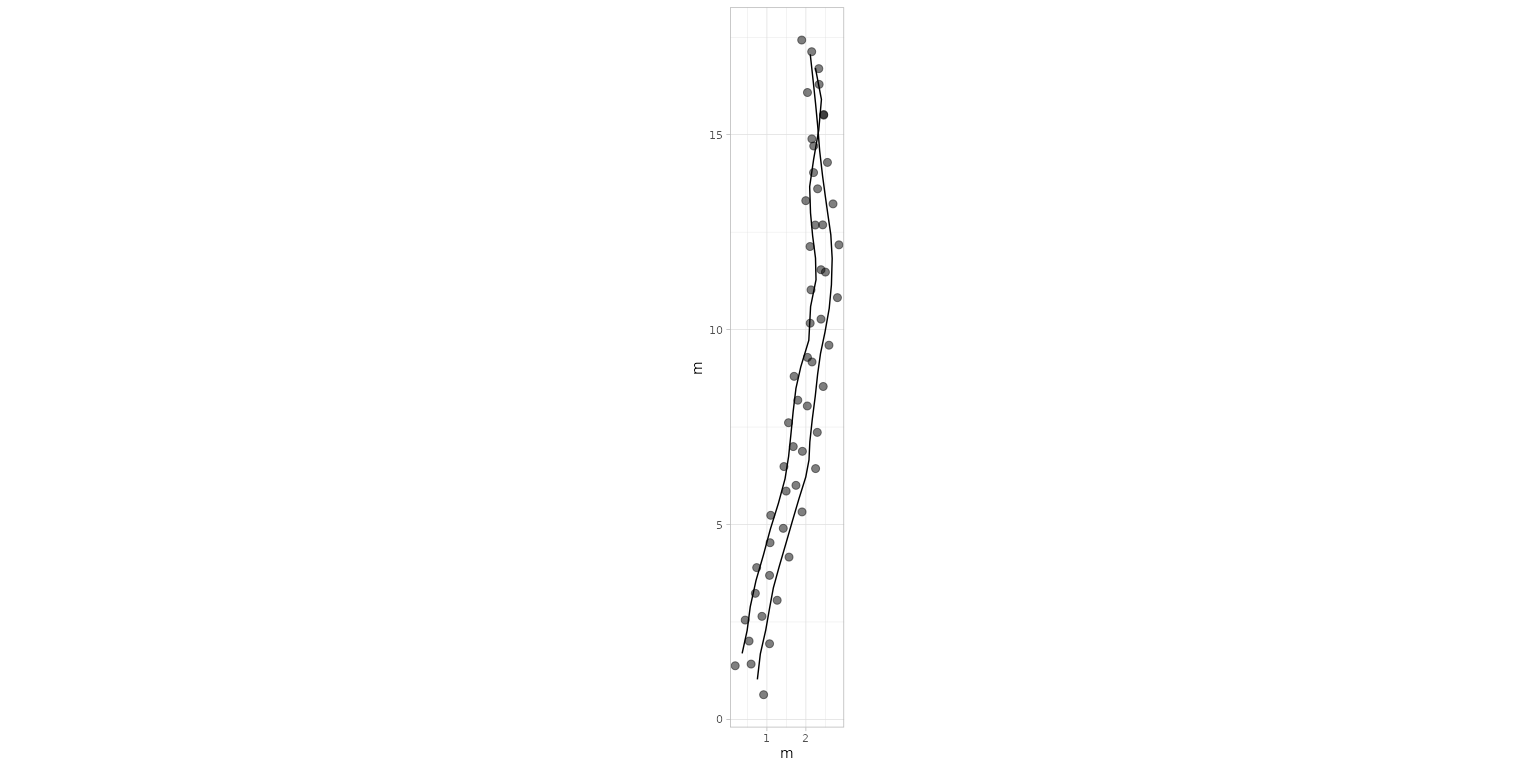
plot_track(MountTom)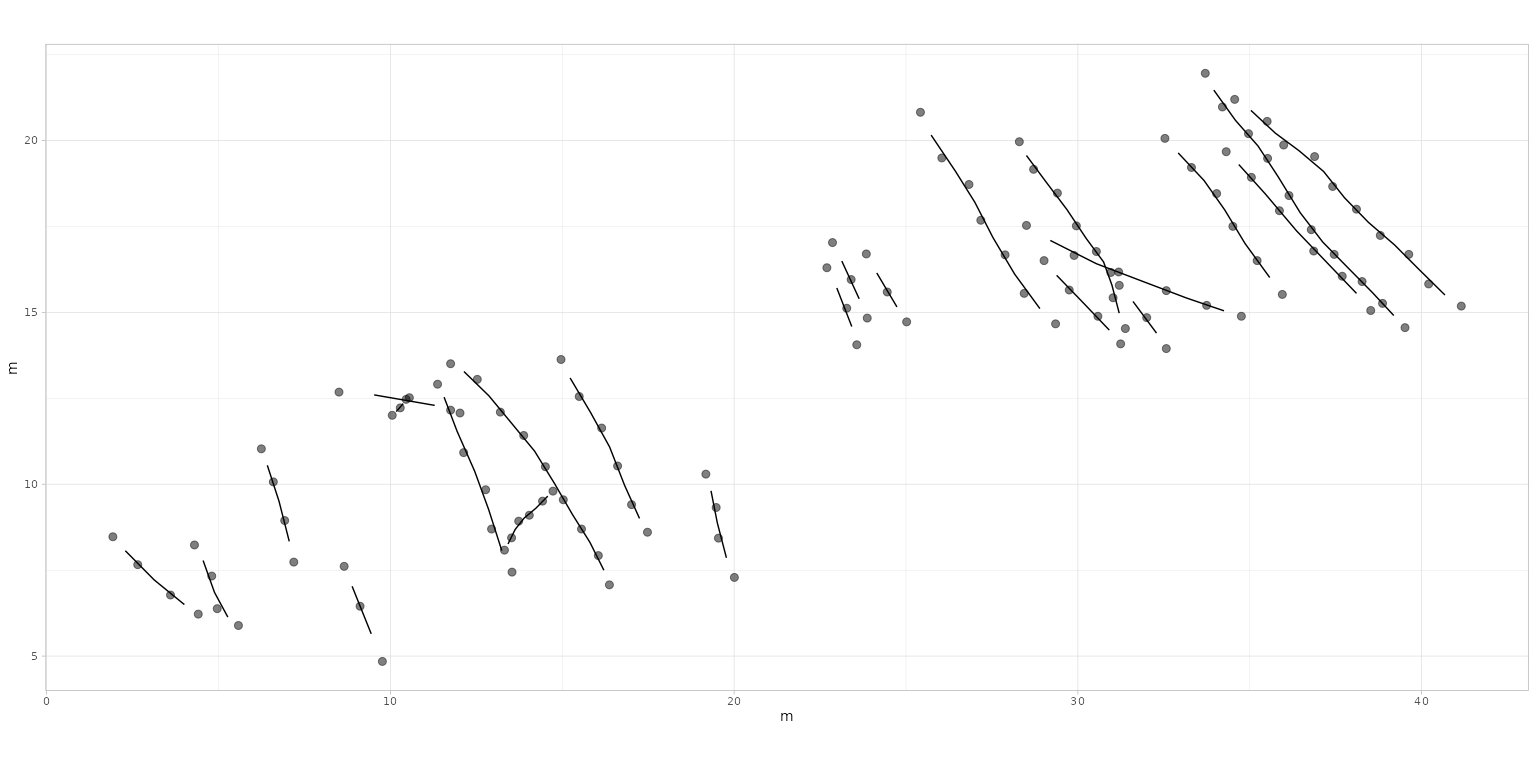
To visualize only the footprint data without the interpolated
trajectories, use the plot = "Footprints" argument. This is
particularly useful when we want to inspect the original footprint
positions without the influence of interpolated trajaectories.
plot_track(PaluxyRiver, plot = "Footprints")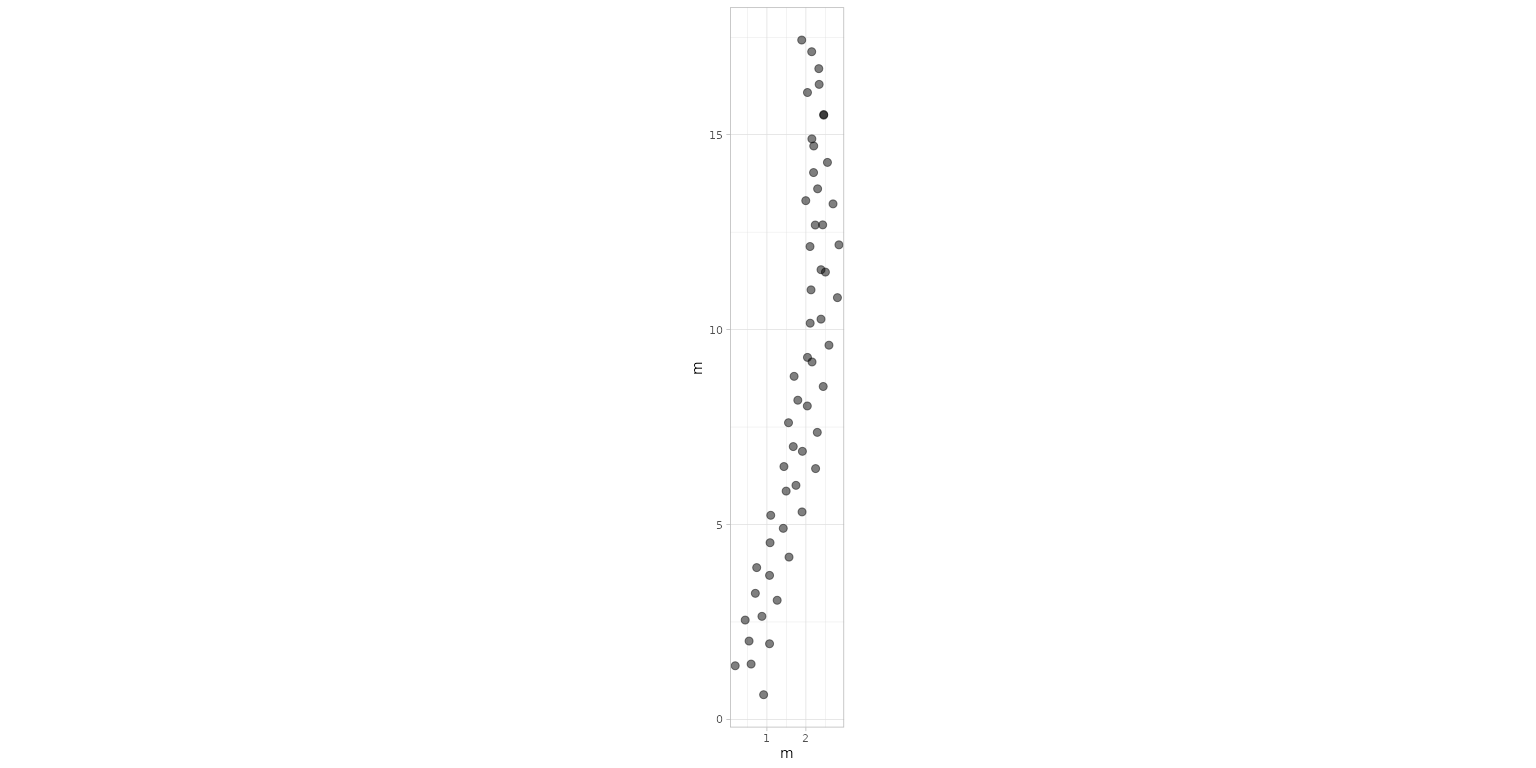
plot_track(MountTom, plot = "Footprints")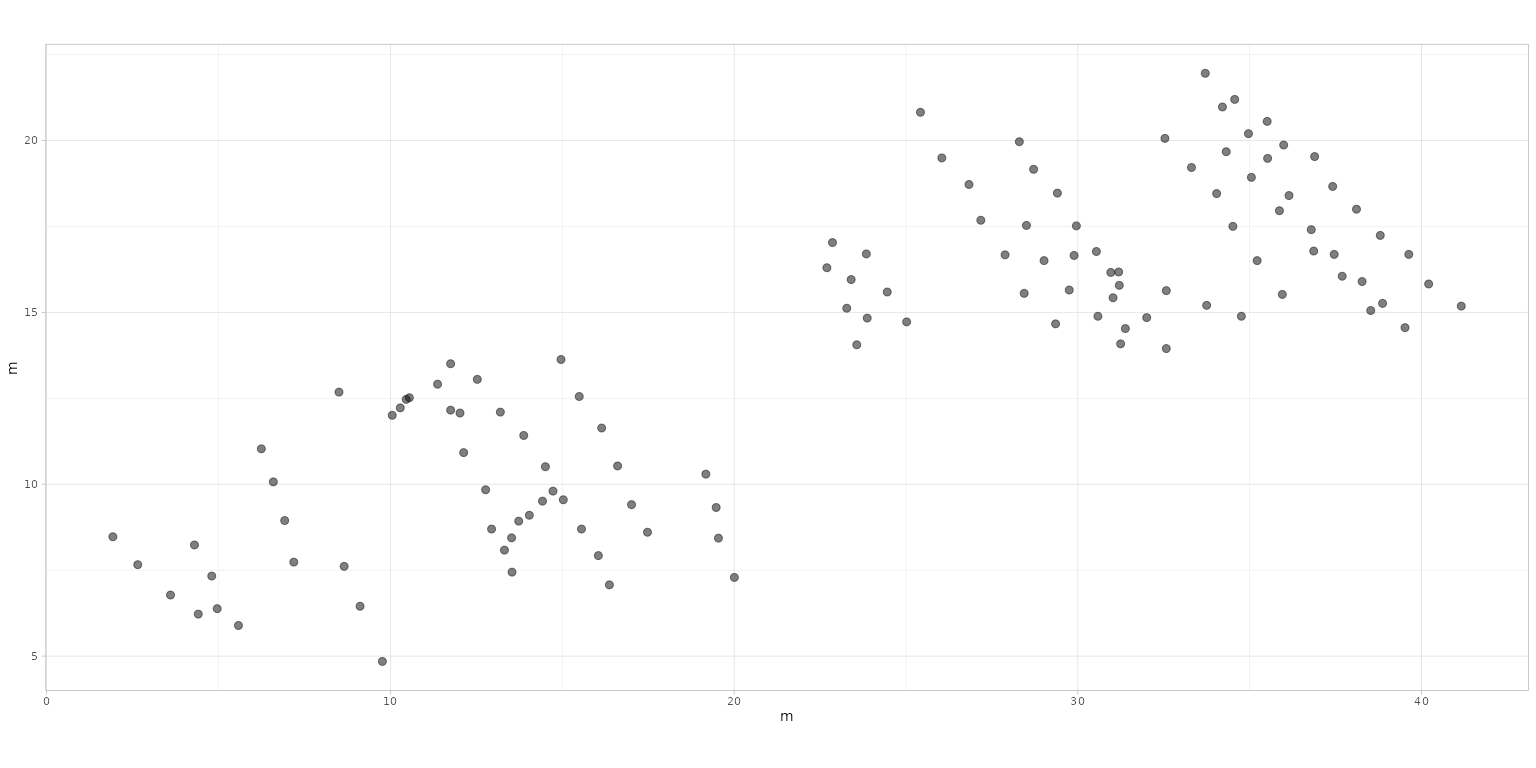
In addition, the correctness of the footprint
sequence along each trackway can be visually assessed using the
seq.foot = TRUE argument, which replaces
footprint points with their sequential numbering. This provides a direct
check that footprints are ordered consistently with the inferred
direction of movement.
plot_track(PaluxyRiver, plot = "FootprintsTrajectories", cex.f = 4, alpha.t = 0.2, seq.foot = TRUE)
plot_track(MountTom, plot = "FootprintsTrajectories", cex.f = 4, alpha.t = 0.2, seq.foot = TRUE)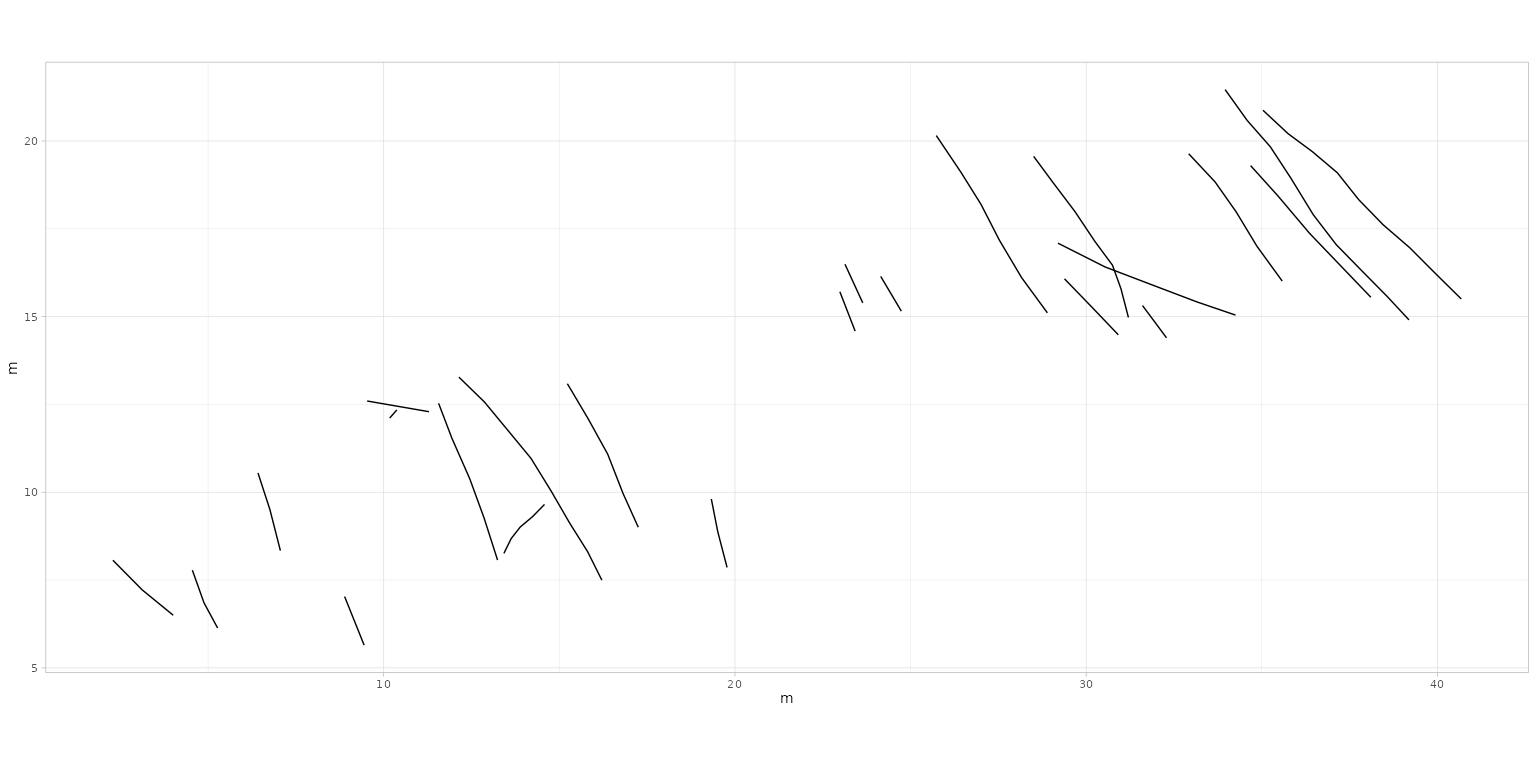
If the goal is to focus exclusively on the interpolated trajectories
without displaying individual footprints, the
plot = "Trajectories" option can be used.
This visualization highlights the overall geometry, continuity, and
spatial pattern of movement along each trackway. When combined with
arrow.t = TRUE, arrowheads are added to
the terminal end of each trajectory, providing an explicit visual
indication of trackway directionality. This is
particularly useful as a quality-control step, allowing users to verify
that trajectories are oriented correctly and that the inferred direction
of movement is consistent with the underlying footprint sequence and
field interpretation. By making directionality explicit, this option
helps detect potential errors in footprint ordering or trajectory
construction prior to downstream analyses.
plot_track(PaluxyRiver, plot = "Trajectories", arrow.t = TRUE, arrow.size = 0.1)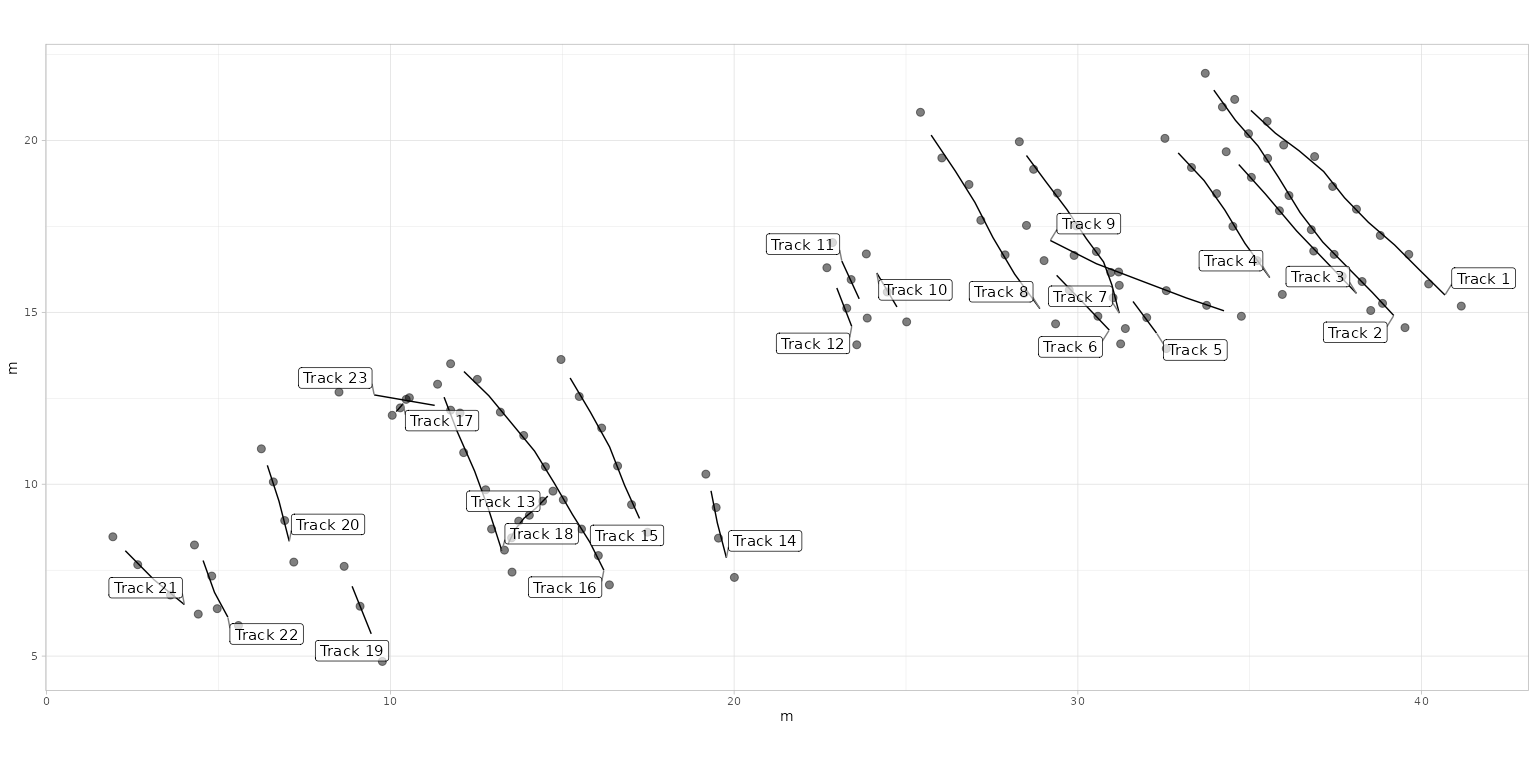
plot_track(MountTom, plot = "Trajectories", arrow.t = TRUE, arrow.size = 0.1)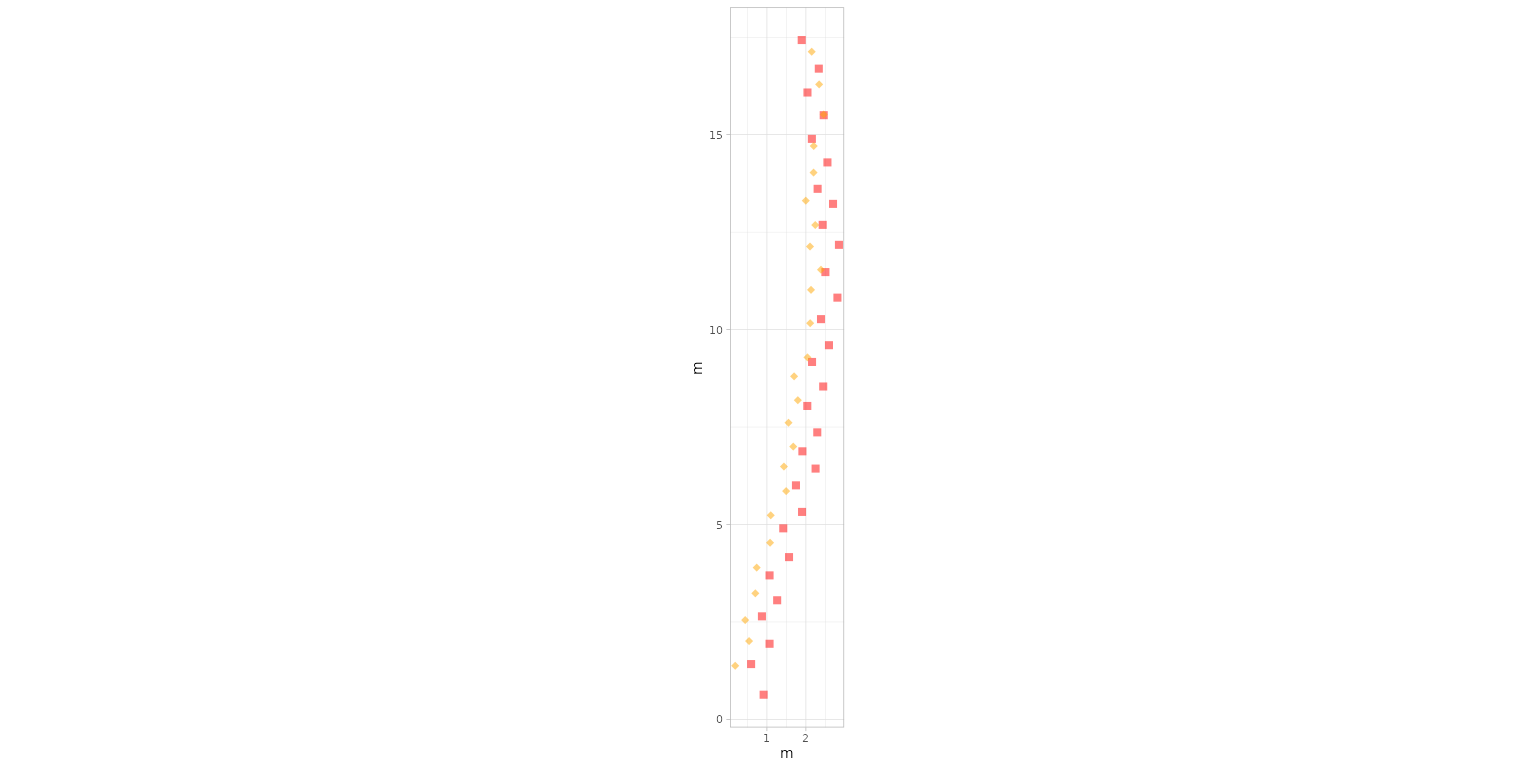
The plot_track() function also allows
labeling individual trackways using the
plot.labels and
labels arguments. In this example,
trackways from the Mount Tom dataset are assigned
custom labels (e.g., “Trackway 1”, “Trackway 2”…)
generated with paste(). Label appearance is customized by
increasing label size (cex.l = 4), adding
padding around labels (box.p = 0.3), and
applying semi-transparency (alpha.l = 0.7)
to improve readability.
labels <- paste("Trackway", seq_along(MountTom[[1]]))
plot_track(MountTom, plot.labels = TRUE, labels = labels, cex.l = 4, box.p = 0.3, alpha.l = 0.7)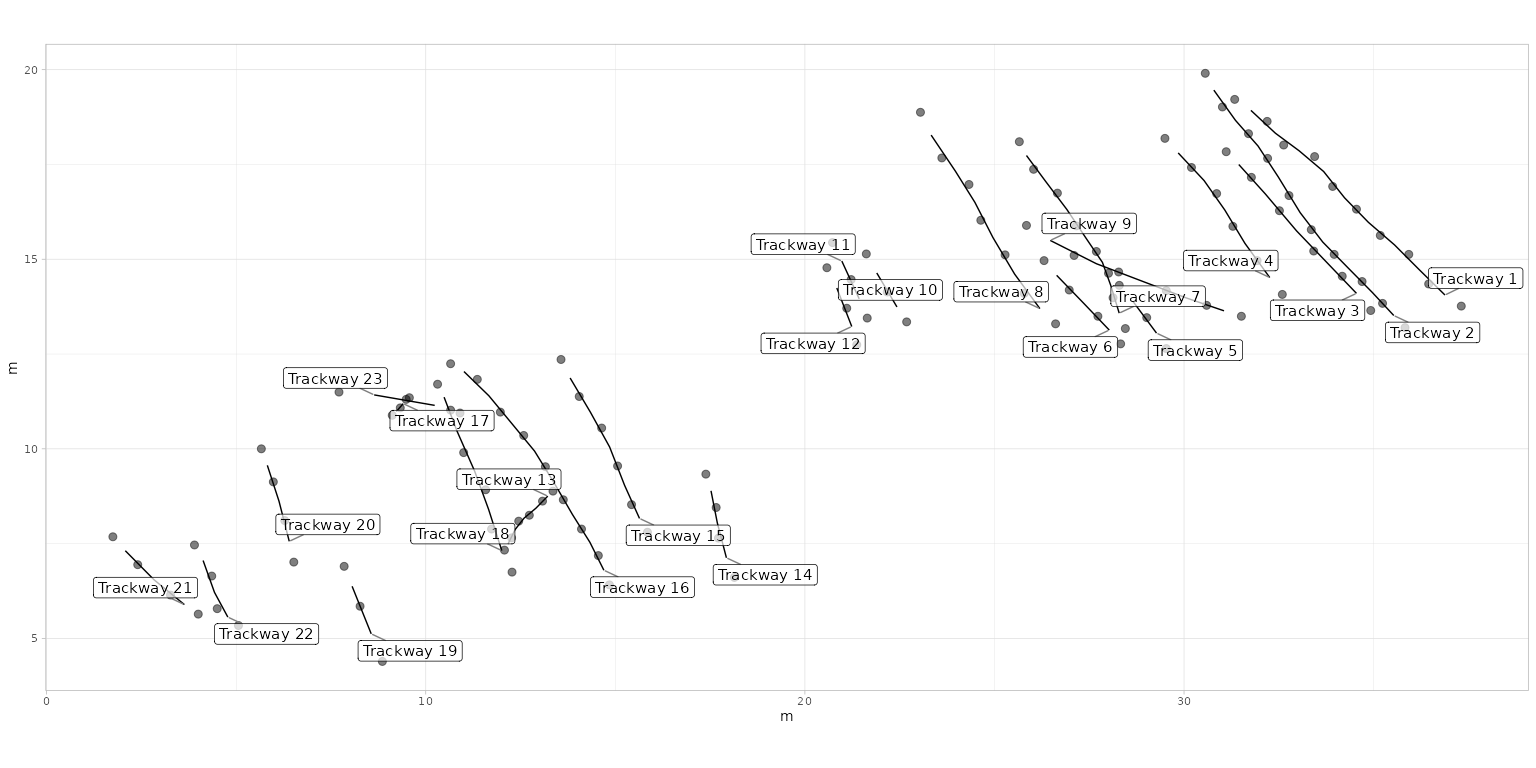
Here, we plot only footprints from the
Paluxy River dataset, using
colours = c("red", "orange") to
distinguish trackways and
shape.f = c(15, 18) to assign different
footprint shapes.
plot_track(PaluxyRiver, plot = "Footprints", colours = c("red", "orange"), shape.f = c(15, 18))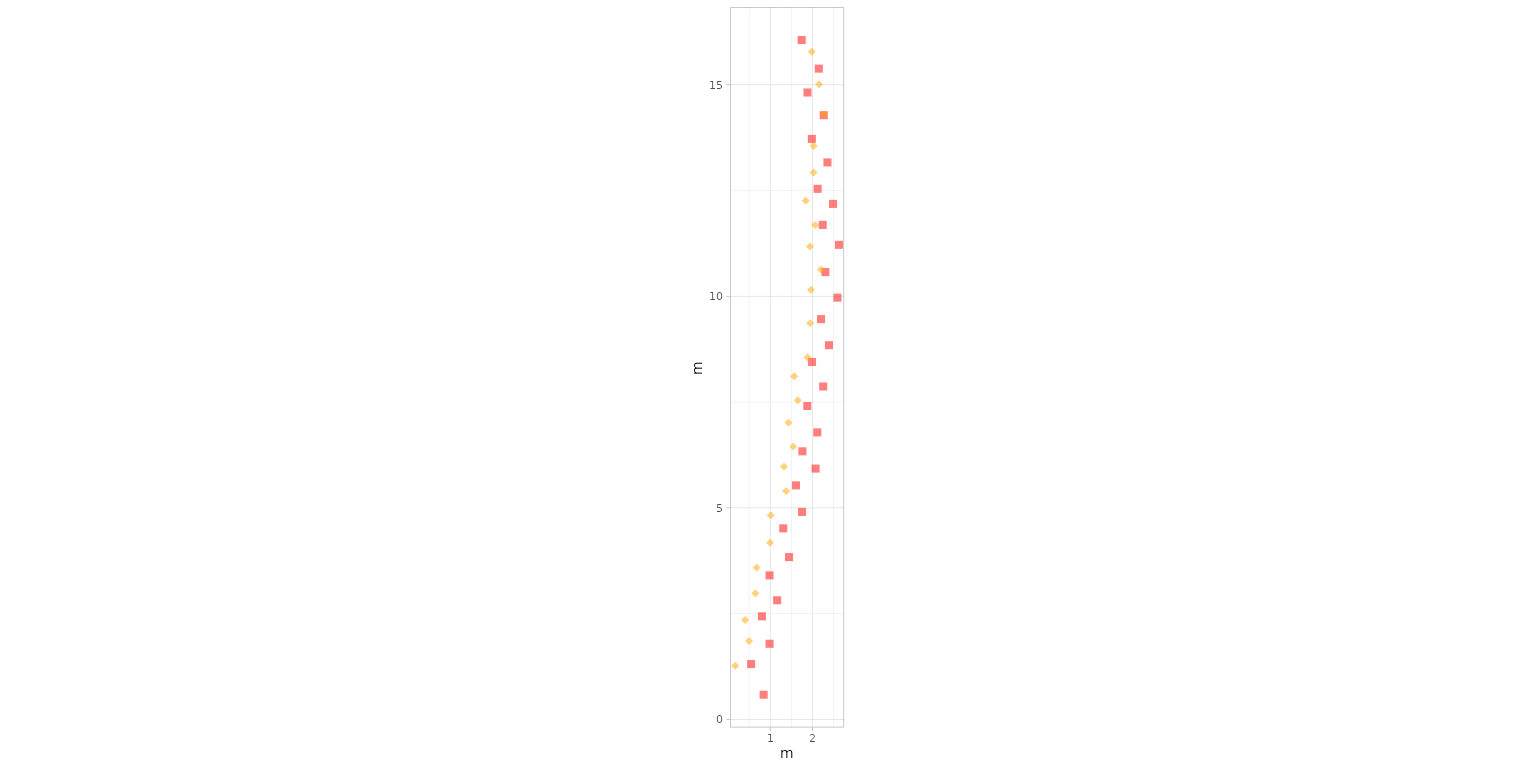
By setting seq.foot = TRUE, footprint
points are replaced by their sequential numbers,
allowing individual footprints to be clearly distinguished and their
order along each trackway to be visually verified.
plot_track(PaluxyRiver, plot = "Footprints", colours = c("red", "orange"), shape.f = c(15, 18), cex.f = 4,seq.foot = TRUE)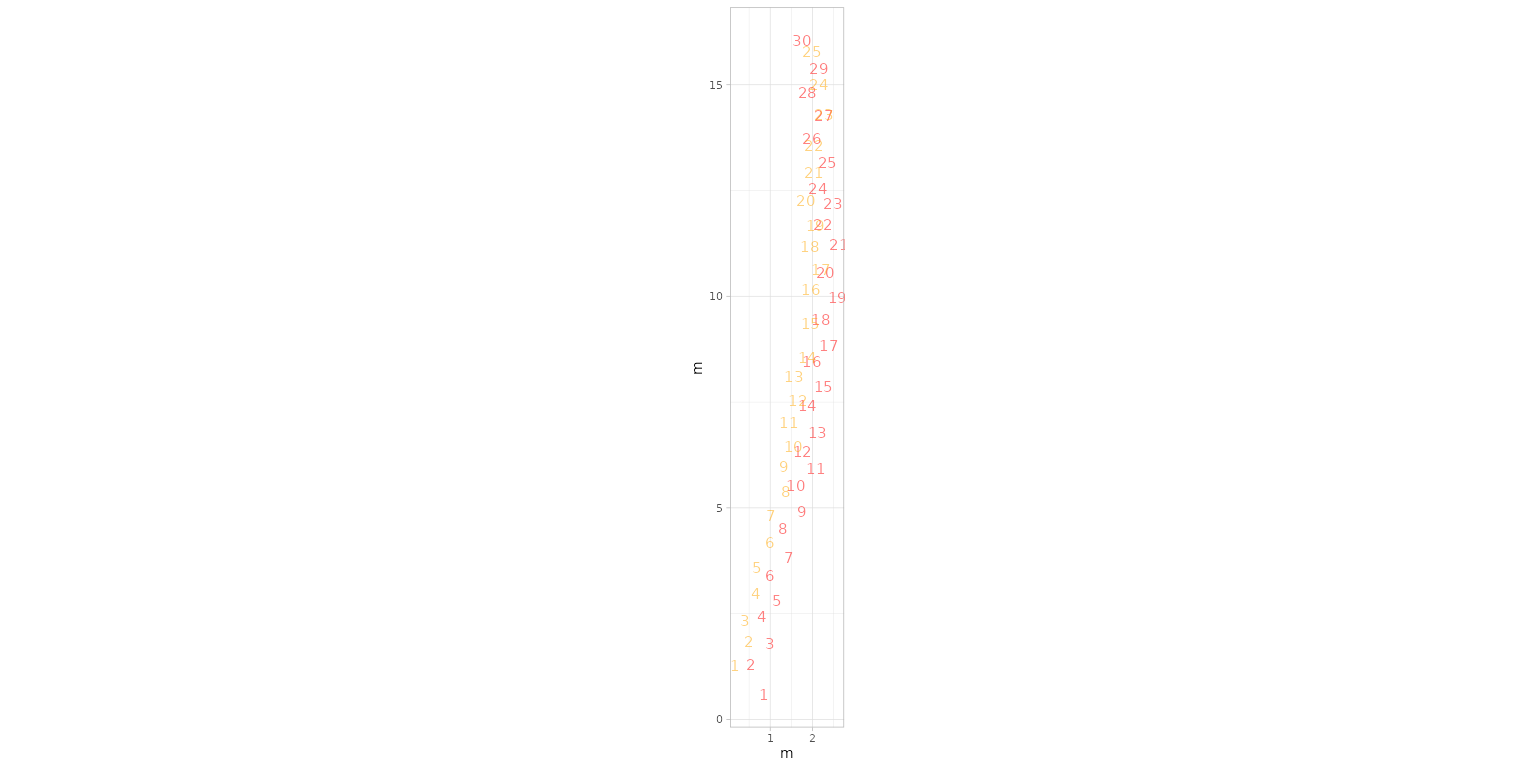
Observer-related uncertainty and reproducibility of digitization
Quantitative analyses of fossil trackways ultimately rely on coordinates placed by human observers. Even when the same trackway is digitized following a standardized protocol, small differences in landmark placement may arise between observers or between repeated digitizations by the same observer. These differences introduce sampling uncertainty that can propagate through all downstream analyses and, if not explicitly evaluated, may obscure or even mimic biological patterns.
To explicitly assess the reproducibility of trackway metrics and to
distinguish genuine biological signal from human-induced noise,
QuAnTeTrack provides the function
observer_error_partitioning(). This
function quantifies how much of the variability in trackway parameters
is attributable to true differences among trackways
versus inter-observer and intra-observer sampling
effects, using replicated digitizations and mixed-effects
modeling.
The logic behind observer_error_partitioning() is
straightforward: if a given parameter primarily reflects biological
differences among trackways, repeated digitizations of the same
trackway—regardless of who digitizes them—should yield similar values.
Conversely, if a parameter is highly sensitive to landmark placement or
digitization choices, a large proportion of its variance will be
associated with observer identity or with replicate-to-replicate
scatter.
By partitioning variance into biologically meaningful and observer-related components, this function allows users to: (1) Audit the reproducibility of digitized trackway data, (2) identify robust metrics suitable for hypothesis testing and clustering, and (3) detect parameters that are dominated by sampling noise and require caution or protocol refinement.
The analysis requires three explicit inputs that together define the
structure of the reproducibility assessment. First, the
data argument takes a
trackway R object containing all replicated
digitizations. Each replicate is treated as an independent
realization of the same underlying biological trackway and must
therefore be included within the same object, rather than split across
multiple files or analyses. Second, the
metadata argument provides the
experimental context of the digitization process. This metadata table
contains one row per entry returned by track_param(data),
in the same order, and specifies which digitizations correspond to the
same biological trackway, which observer produced them, and how many
replicate attempts were made. By explicitly encoding track identity,
observer identity, and replicate structure, this table allows the
function to disentangle biological variation from inter- and
intra-observer sampling effects. Finally, the
variables argument defines which trackway
parameters are evaluated. By default, the function considers a broad set
of directional, kinematic, and geometric metrics (including turning
angles, distances, step-length statistics, sinuosity, straightness,
trackway width, and pace angulation). Users may restrict this set to a
subset of parameters when focusing on specific aspects of trackway
geometry or when evaluating the robustness of particular metrics prior
to hypothesis testing.
The function requires that all replicated
digitizations—across observers and/or repeated attempts—are
bundled into a single trackway R object. Each replicate is
treated as an independent entry and must be accompanied by a
corresponding row in a metadata table describing:
- The biological track ID,
- The observer who digitized it,
- The replicate index within each observer–track combination.
For each selected trackway parameter,
observer_error_partitioning() fits a mixed-effects model
that decomposes variance into four conceptual components:
-
Between-track variance (
track) — interpreted as biological signal, -
Between-observer variance (
observer) — inter-observer sampling error, -
Observer × track interaction
(
observer:track) — observer-specific bias tied to particular tracks, - Residual variance — intra-observer sampling error (replicate-to-replicate scatter).
Random-effect terms that cannot be estimated (e.g., factors with only one level) are automatically excluded, allowing the function to adapt to different experimental designs (inter-only, intra-only, or combined).
Angular parameters, such as turning angles and pace angulation, are treated using a sine–cosine transformation to respect their circular nature and to avoid artificial discontinuities at 0°/360°. Variance components are estimated independently in sine and cosine space and then averaged.
To facilitate interpretation, the function summarizes robustness using a signal-to-noise ratio (SNR), defined as the ratio between biological variance and the total sampling-related variance (observer, observer × track, and residual components). As a practical guideline:
- Low SNR (< 1) indicates that observer-related uncertainty exceeds biological signal,
- Intermediate SNR (~1–2) suggests comparable biological and sampling contributions,
- High SNR (> 2) indicates that biological differences dominate and the metric is robust.
This information is particularly useful for deciding which parameters can be confidently interpreted in downstream analyses and which should be treated with caution.
observer_error_partitioning() returns an
"error_partitioning" object that includes:
- A summary table reporting variance components and their relative contributions for each parameter,
- A signal-to-noise table quantifying biological versus sampling variance,
- A compact quality-control table that classifies each metric according to robustness and identifies the dominant source of variance,
- The fitted mixed-effects models used in the analysis, along with the underlying analysis table and model formulas.
Together, these outputs provide both a quantitative and an intuitive assessment of digitization reliability.
Anatomical uncertainty and landmark-fidelity effects
Even when trackways are digitized by a single observer following a consistent protocol, fossil footprints are rarely preserved with perfect anatomical fidelity. Erosion, deformation, substrate collapse, or incomplete preservation may obscure the precise position of biologically meaningful reference points, introducing uncertainty that is independent of who digitizes the material. This form of uncertainty is intrinsic to the fossil record and reflects limitations in anatomical preservation rather than the human sampling process.
To explicitly quantify the impact of this source of uncertainty,
QuAnTeTrack provides the function
anatomical_error_partitioning(). This
function evaluates how much of the variability in trackway parameters
can be attributed to imprecision in landmark placement caused by
anatomical or taphonomic factors, as opposed to genuine
biological differences among trackways. In contrast to observer-based
approaches, this function relies exclusively on simulation and does not
incorporate observer identity or replicated digitizations.
The logic behind anatomical_error_partitioning() is
conceptually analogous to a sensitivity analysis. Rather than asking
whether different observers obtain similar results, it asks a different
question: if the anatomical reference points of footprints were
slightly misplaced within a realistic spatial tolerance, how much would
the resulting trackway parameters change? Parameters that remain
stable under such perturbations can be considered robust to
preservation-related uncertainty, whereas parameters that vary strongly
are more sensitive to landmark fidelity and should be interpreted with
caution.
The analysis operates on a single trackway R object
containing the original digitized data. Landmark uncertainty is
introduced by repeatedly perturbing footprint coordinates within a
user-defined spatial tolerance, specified via an error
radius that represents expected imprecision in reference-point
placement. This tolerance may be applied uniformly to all trackways or
allowed to vary among trackways to reflect heterogeneous preservation
quality across a site.
For each simulation, footprint landmarks are randomly displaced within the specified tolerance, the medial trajectory is reconstructed following the same procedure used for the original data, and trackway parameters are recalculated. Repeating this process across many Monte Carlo simulations generates a distribution of values for each parameter that reflects anatomical noise alone, without any contribution from observer effects.
The resulting variability is then decomposed into two primary components: variability among trackways, interpreted as biological signal, and variability generated within trackways by simulated landmark perturbations, interpreted as anatomical uncertainty. Angular parameters, such as turning angles and pace angulation, are handled using a sine–cosine transformation to respect their circular nature and avoid artificial discontinuities.
As in the observer-based framework, robustness is summarized using a signal-to-noise ratio (SNR), defined here as the ratio between between-track (biological) variance and variance introduced by anatomical uncertainty. Low SNR values indicate that a parameter is strongly affected by landmark fidelity, whereas high SNR values indicate that biological differences dominate despite plausible levels of anatomical imprecision.
anatomical_error_partitioning() returns an
"error_partitioning" object that mirrors the structure used
for observer-related uncertainty, facilitating direct comparison between
the two sources of error. The output includes a summary of variance
components for each parameter, signal-to-noise ratios, and a compact
quality-control table identifying which metrics are most sensitive to
anatomical uncertainty.
By explicitly quantifying the effects of landmark fidelity, this function provides a critical complement to observer-based error assessment. Together, these approaches allow users to disentangle uncertainty arising from the fossil record itself from uncertainty introduced during digitization, and to identify trackway parameters that remain interpretable despite imperfect preservation.
Example usage and interpretation
In the examples below, anatomical uncertainty is explored by progressively increasing the spatial tolerance applied to footprint landmarks. As the assumed imprecision increases, parameters that are sensitive to landmark fidelity typically show increasing anatomical variance and decreasing signal-to-noise ratios, whereas robust parameters remain comparatively stable.
Extracting Track Parameters
The track_param() function is designed
to compute and display various parameters related to the
movement patterns of tracks from a
track R object. This function is essential
for extracting detailed information about the structure of
individual tracks and their spatial
relationships, providing key metrics that can be used for
further analysis, comparison, and visualization. The
track_param() function utilizes several
helper functions from the trajr package,
which is commonly applied in animal movement
analysis.
The track_param() function works by
iterating over each trajectory within the provided track data and
computing a set of movement-related parameters. These
include turning angles, step lengths,
total distances covered, track
lengths, and measures of sinuosity and
straightness. Such parameters are crucial for understanding the
locomotor patterns of trackmakers and assessing their
movement efficiency.
The turning angles are calculated using the
trajr::TrajAngles() function, providing a
measure of directional changes at each step. The
mean turning angle and standard
deviation are also calculated to summarize overall turning
behavior. The distance covered by the track is obtained
using the trajr::TrajDistance() function,
which measures the total straight-line distance between
the start and end points of the track. The track length
is calculated using the
trajr::TrajLength() function, which sums
the distances between all consecutive points in the track. The
step lengths, representing the distances between
consecutive points, are calculated with
trajr::TrajStepLengths(). The function
also computes the mean and standard deviation of these step
lengths. The sinuosity of the track is
calculated using the
trajr::TrajSinuosity2() function, which
quantifies how much a path deviates from a straight line. This measure
of sinuosity is based on the method described by Benhamou
(2004), which refines previous methods to provide more accurate
estimates of tortuosity for paths with varying turning angles and step
lengths. The straightness index is calculated with
trajr::TrajStraightness(), defined as the
ratio between the beeline distance (start to end) and the total path
length. This measure is based on the work of Batschelet (1981)
and provides insight into how direct or meandering the movement of the
trackmaker was.
The calculation of sinuosity is based on the
formula:
where:
- is the mean step length (in meters),
- is the mean cosine of turning angles (in radians), and
- is the coefficient of variation of the step length (in meters).
The straightness index is calculated as the ratio , where is the beeline distance between the first and last points of the trajectory, and is the total path length. This index is particularly useful for comparing the efficiency of directed walks, but it is not suitable for random trajectories, where the index tends towards zero with increasing steps.
The track_param() function returns a
list of lists, where each sublist contains the
computed parameters for a corresponding track. The
parameters include: turning angles, mean
turning angle, standard deviation of turning
angles, distance, length,
step lengths, mean step length,
standard deviation of step length,
sinuosity and straightness.
The reference direction for calculating angles is considered to be along the positive x-axis, with angles measured counterclockwise. The computed parameters are returned in a structured format, allowing users to further process or visualize the data as needed.
The track_param() function provides
valuable insights into the structure and efficiency of
trackmaker movements, making it a crucial tool for analyzing
fossil trackways.
Examples of Usage
The track_param() function extracts
movement parameters such as turning angles, step lengths, distances,
track lengths, sinuosity, and straightness from
track R objects. The examples below
calculate these parameters for the Paluxy River and
Mount Tom datasets.
params_paluxy <- track_param(PaluxyRiver)
params_mount <- track_param(MountTom)Calculating Velocities and Relative Stride Lengths
The velocity_track() function
calculates the velocities and relative stride
lengths for each step within a series of tracks. It requires a
track R object as input, which contains
both trajectories and footprints, and uses the
height at the hip, H, for each track maker
to estimate speed. The H argument should be supplied as a
numeric value representing the hip height in meters. If the hip height
is unknown, it must be estimated from skeletal proportions or other
anatomical information. The accuracy of velocity calculations depends
heavily on providing a realistic value for this parameter. The function
supports two calculation methods: Method A
(Alexander, 1976) and Method B (Ruiz &
Torices, 2013), which are specified via the method
argument. By default, Method A is applied to all tracks
if no method is specified. The gravitational
acceleration, G, is set to 9.8
m/s2 by default.
This function works by first extracting the track data and then calculating the Euclidean distance between consecutive footprints to determine the stride length. For each step, the velocity is calculated using one of the two methods.
Method A applies the formula (Alexander, 1976):
where is the velocity (m/s), is gravitational acceleration (m/s2), is stride length (m), and is the hip height (m). This method is based on empirical studies that model the relationship between stride length, body size, and speed for general terrestrial vertebrates. The coefficients , , and have been derived from studies focused on scaling relationships in bipedal and quadrupedal animals.
Method B follows a similar approach but with a coefficient of instead of , which provides a refinement for bipedal locomotion. The formula is (Ruiz & Torices, 2013):
The relative stride length is calculated as the ratio between stride length and hip height (), which allows distinguishing between different gaits according to Thulborn & Wade (1984). The classification is as follows:
-
Walk: Relative stride
(locomotor performance equivalent to walking in mammals).
-
Trot: Relative stride
(locomotor performance equivalent to trotting or racking in
mammals).
- Run: Relative stride (locomotor performance equivalent to cantering, galloping, or sprinting in mammals).
The function returns a track
velocity object, which is structured as a
list of lists, with each list representing an
individual track. For each track, the output includes various metrics
that describe the calculated velocities and relative stride lengths.
Specifically, it provides a vector of calculated velocities for each
step, referred to as Step_velocities,
measured in meters per second (m/s). Additionally, the
function calculates the Mean_velocity,
which represents the average speed across all steps, as well as the
Standard_deviation_velocity, which
quantifies the variation in velocity measurements. The
Maximum_velocity and
Minimum_velocity indicate the highest and
lowest calculated velocities, respectively. In terms of relative stride
lengths, the function also provides a vector of calculated values known
as Step_relative_stride. The average of
these values is captured by the
Mean_relative_stride, while their
variation is described by the
Standard_deviation_relative_stride.
Moreover, the highest and lowest calculated relative stride lengths are
denoted as Maximum_relative_stride and
Minimum_relative_stride, respectively.
This comprehensive output allows users to thoroughly assess the speed
and locomotion style of the track-makers under study.
The function is particularly useful for estimating the speed of ancient track-makers from their footprints and evaluating their locomotion style (walking, trotting, or running).
Examples of Usage
Calculating velocities for the Paluxy River dataset
using Method A for both tracks. The hip heights
(H_paluxyriver) are provided for each trackmaker.
H_paluxyriver <- c(3.472, 2.200)
velocity_paluxyriver <- velocity_track(PaluxyRiver, H = H_paluxyriver)Calculating velocities for the Mount Tom dataset
using Method A for all tracks. Multiple hip heights
(H_mounttom) are specified, corresponding to each track in
the dataset.
H_mounttom <- c(
1.380, 1.404, 1.320, 1.736, 1.364, 1.432, 1.508, 1.768, 1.600,
1.848, 1.532, 1.532, 0.760, 1.532, 1.688, 1.620, 0.636, 1.784, 1.676, 1.872,
1.648, 1.760, 1.612
)
velocity_mounttom <- velocity_track(MountTom, H = H_mounttom)Comparing velocities for the Paluxy River dataset using different methods: Method A for the sauropod trackway and Method B for the theropod trackway. This demonstrates how to apply distinct calculation methods to different trackmakers within the same dataset.
H_paluxyriver <- c(3.472, 2.200)
Method_paluxyriver <- c("A", "B")
velocity_paluxyriver_diff <- velocity_track(PaluxyRiver, H = H_paluxyriver, method = Method_paluxyriver)Plotting Velocity Data
The plot_velocity() function provides a
powerful visualization tool for examining trajectories colored by either
velocity or relative stride length. By
applying color gradients, it highlights how these parameters change
along the paths of various tracks, providing valuable insights into
locomotor dynamics.
The function takes as inputs a track R
object and a track velocity R
object, where the latter contains the calculated velocities and
relative stride lengths for each track. The user can specify the
parameter to be visualized via the param
argument, choosing between "V" for
velocity or "RSL" for relative stride
length. If not specified, the function defaults to visualizing
velocity.
The plotting process is handled by the
ggplot2 package, using
ggplot2::geom_path() to plot the tracks
and ggplot2::scale_color_gradientn() to
apply a color gradient representing the selected parameter. Users can
customize the color palette via the
colours argument and adjust the line width
with the lwd argument.
The function also allows the user to include or exclude a legend from
the plot by setting the legend argument to
TRUE or
FALSE, respectively. This flexibility
ensures that the plots can be tailored to the user’s preferences and
presentation requirements.
The resulting plot provides a visually appealing and informative representation of how velocity or relative stride length changes along each trajectory. Such plots are particularly useful for comparing the locomotor patterns of different track makers or assessing how environmental or anatomical factors influence movement.
Examples of Usage
Plotting trajectories colored by relative stride length
(RSL) for the PaluxyRiver dataset using the
previously calculated velocity_paluxyriver_diff object.
plot_velocity(PaluxyRiver, velocity_paluxyriver_diff, param = "RSL")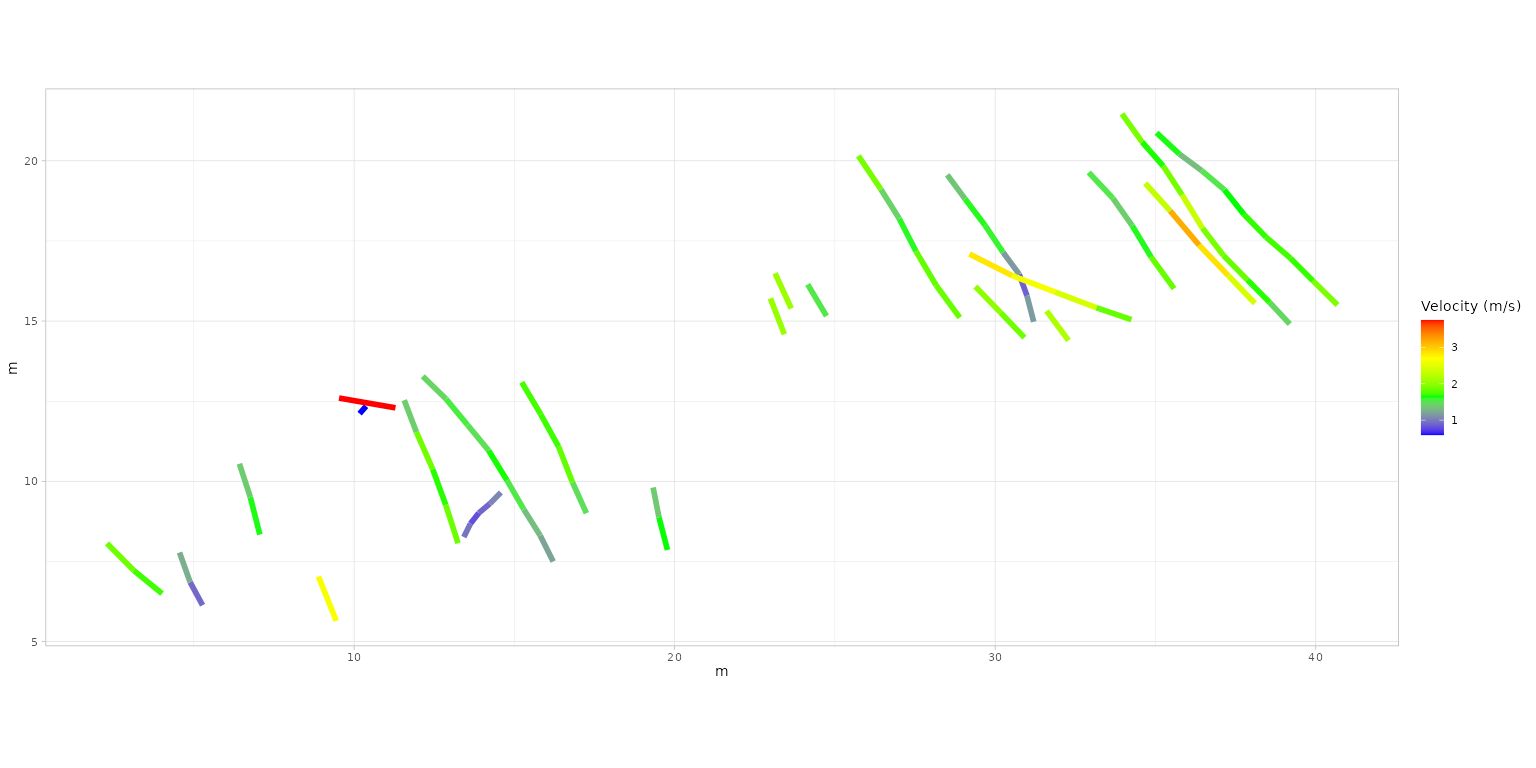
Plotting trajectories colored by velocity for the
MountTom dataset using the previously calculated
velocity_mounttom object.
plot_velocity(MountTom, velocity_mounttom, param = "V")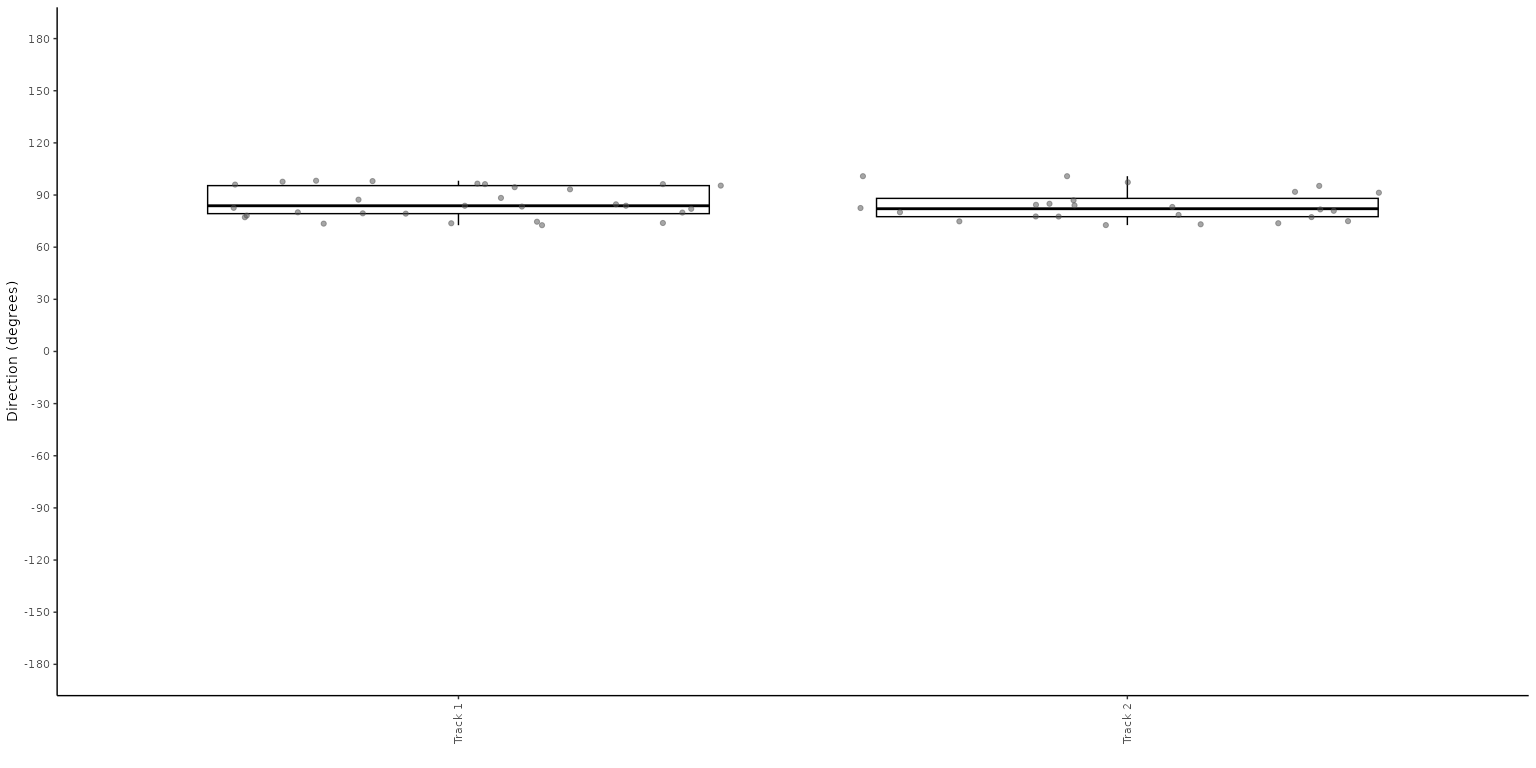
Generating a clean visualization of relative stride length (RSL) for the PaluxyRiver dataset without displaying a legend.
plot_velocity(PaluxyRiver, velocity_paluxyriver_diff, param = "RSL", lwd = 1.5,
colours = c("purple", "orange", "pink", "gray"), legend = FALSE)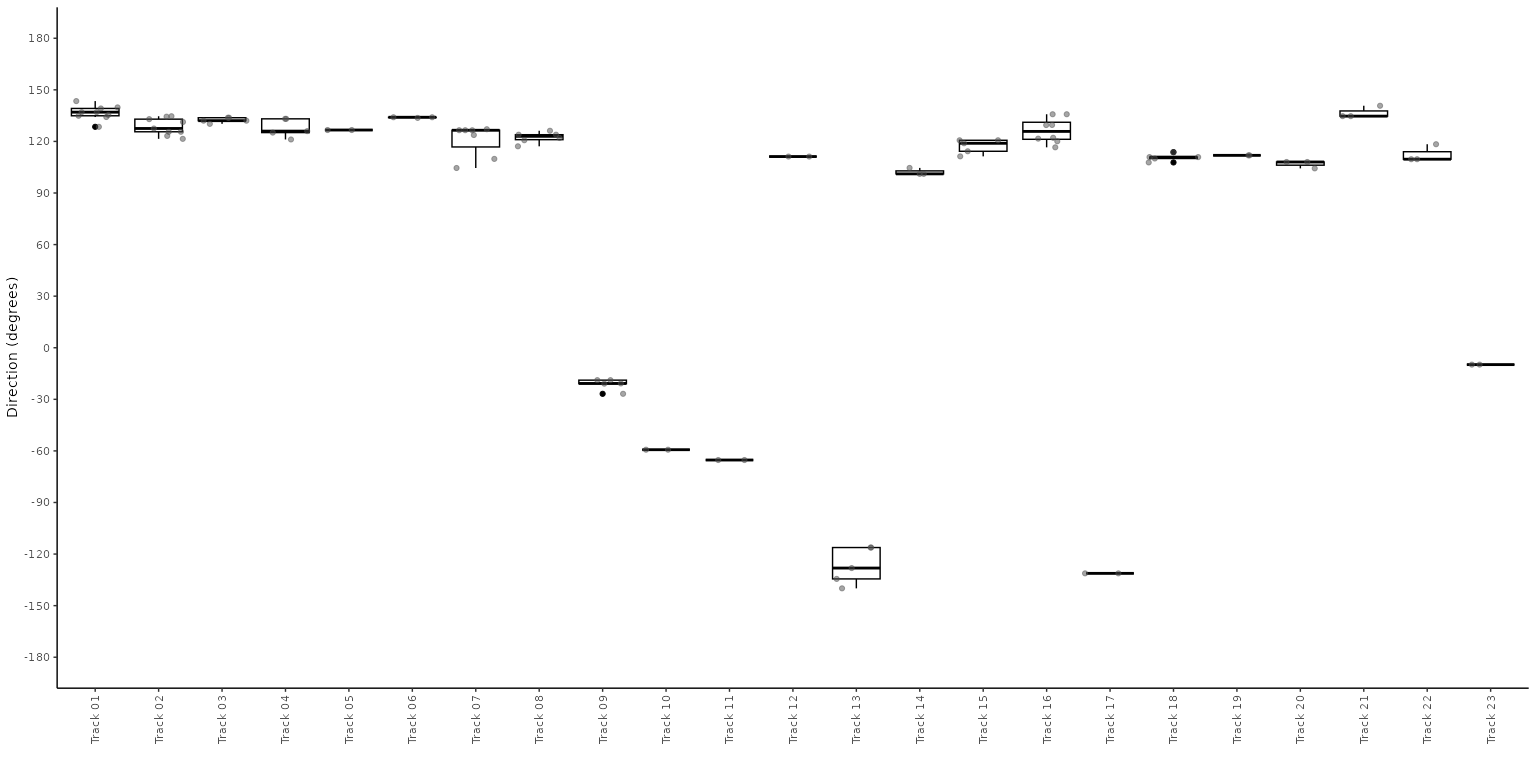
Applying custom colors and increased line width to enhance visualization of velocity patterns for the MountTom dataset.
plot_velocity(MountTom, velocity_mounttom, param = "V", lwd = 2,
colours = c("blue", "green", "yellow", "red"))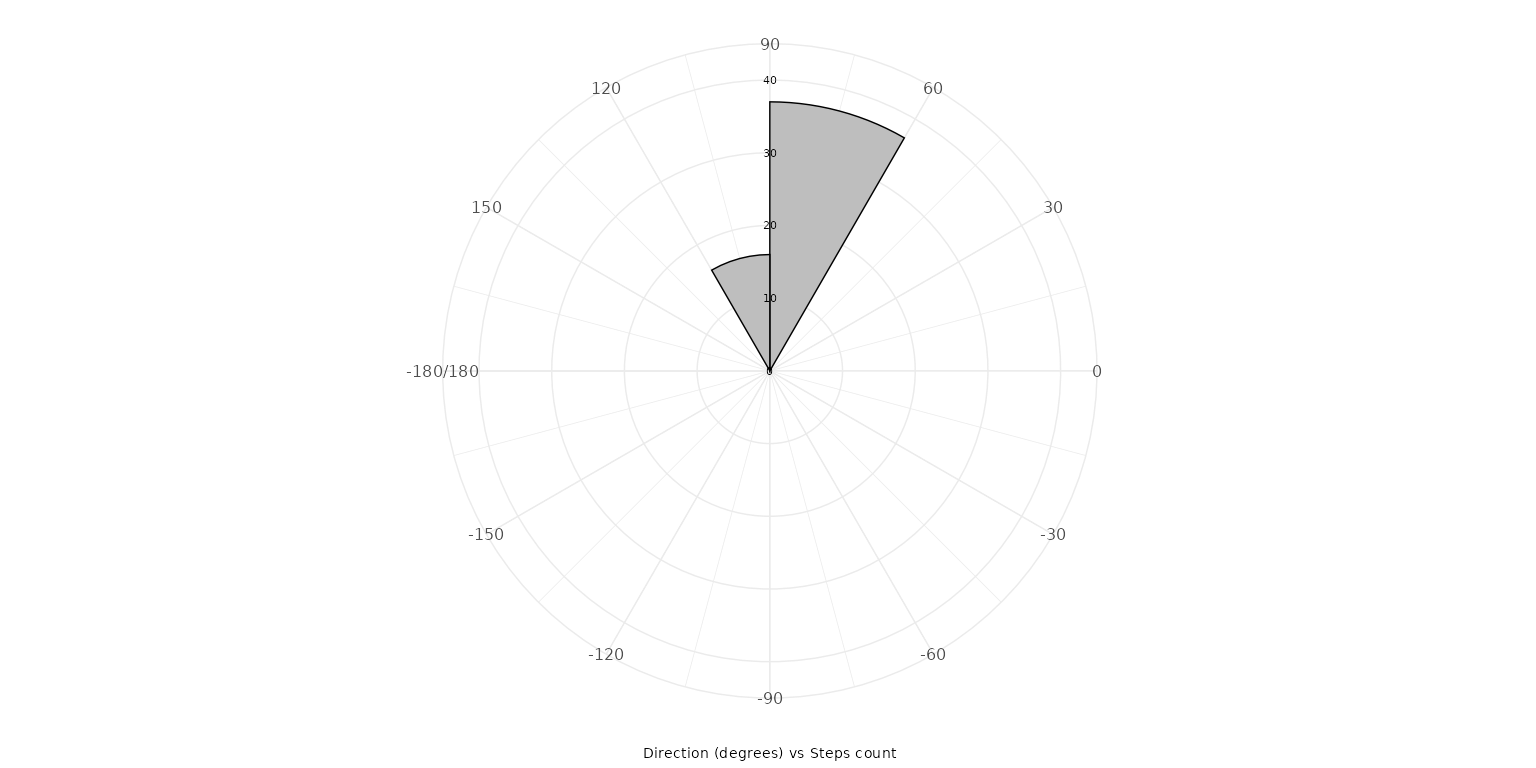
Plotting Direction Data
The plot_direction() function provides
a comprehensive approach to visualizing direction data
from track R objects. It allows users to
generate various types of plots to effectively compare and examine
directionality within their datasets. The available plotting styles are
highly customizable, making this function versatile for different types
of directional analysis.
This function supports four primary plotting styles,
specified by the plot_type argument. The
"boxplot" option displays the distribution
of step directions across tracks as boxplots, providing an overview of
directionality variations by showing medians, quartiles, and potential
outliers. The "polar_steps" option
generates polar histograms that visualize the frequency
of steps within various directional bins, making it particularly useful
for examining the spread and density of step directions around a central
point and highlighting dominant movement trends. The
"polar_average" style also produces
polar histograms, but it focuses on average directions
per track rather than individual steps. This summarization approach
offers a simplified comparison of overall trends across multiple tracks.
Finally, the "faceted" option creates
faceted polar histograms where each track is displayed
separately within a grid of plots, providing a clear visual comparison
of step directions across tracks and making it especially effective for
analyzing individual trackmaker behaviors.
The plot_direction() function allows
users to customize visualizations through several
arguments. The angle_range argument
controls the width of the bins used in polar
histograms, allowing users to specify the desired
angular resolution. The
y_labels_position argument is useful for
positioning the labels of the y-axis, especially in
polar plots, to enhance clarity and presentation. Users can also provide
custom breaks for the y-axis using the
y_breaks_manual argument, which defines
where the labels should be placed for better visualization of frequency
data. This flexibility ensures that the user can tailor the
output to suit specific analytical needs, whether examining
general trends, comparing individual
tracks, or highlighting particular aspects of
directional data.
By generating high-quality visualizations as
ggplot R objects, the
plot_direction() function allows for
further customization using additional functions from the
ggplot2 package. This integration makes it
easy to enhance plots with annotations, themes, and other graphical
elements.
The function is particularly useful for analyzing trackway direction data, providing valuable insights into movement patterns, orientation preferences, and potential group behavior.
Examples of Usage
The boxplot option generates a summary
of directional data distribution, highlighting central tendency,
variability, and potential outliers across tracks.
plot_direction(PaluxyRiver, plot_type = "boxplot")
plot_direction(MountTom, plot_type = "boxplot")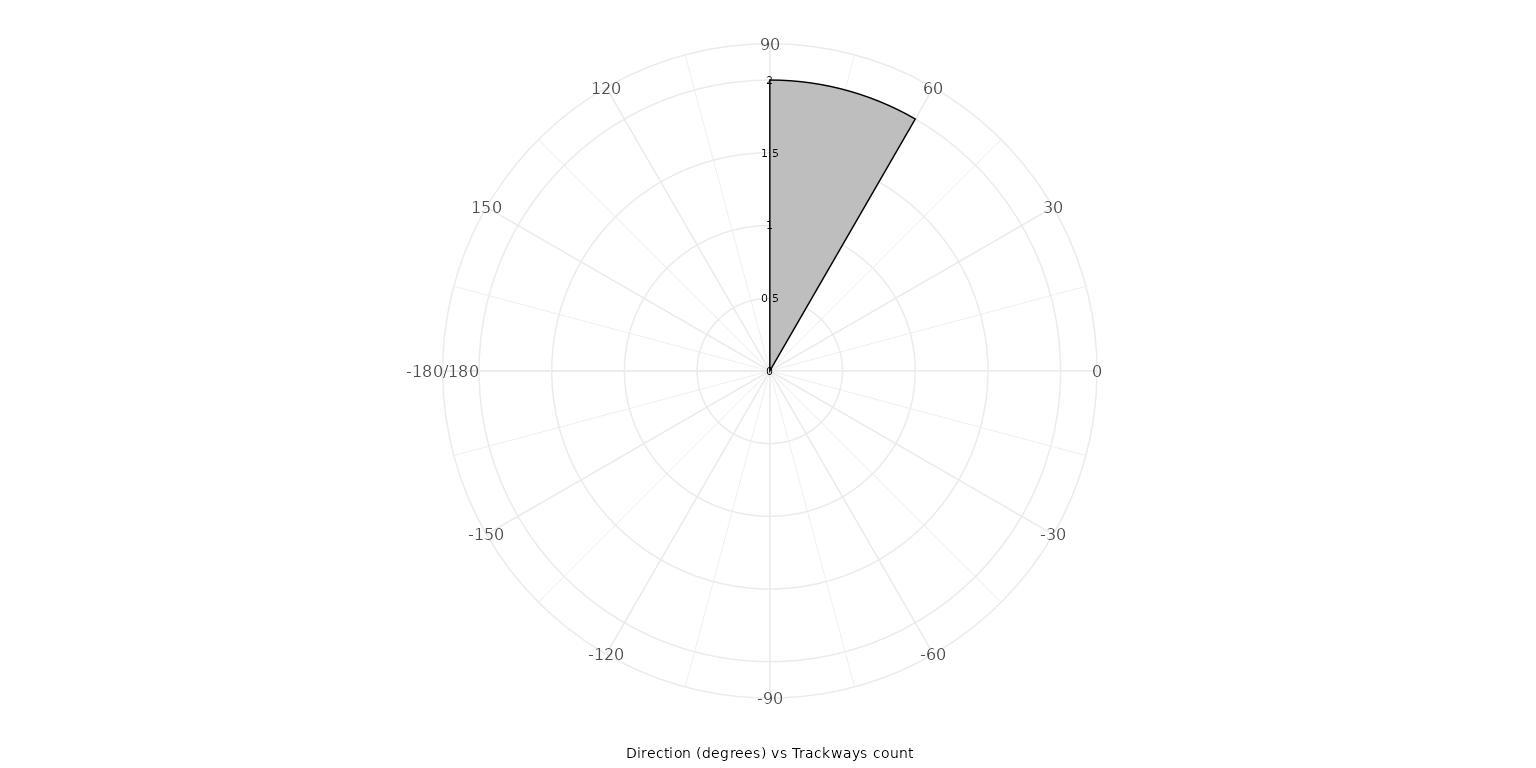
The polar_steps option creates a polar
histogram of individual steps radiating from a central point, revealing
the angular spread of movement and dominant directions.
plot_direction(PaluxyRiver, plot_type = "polar_steps")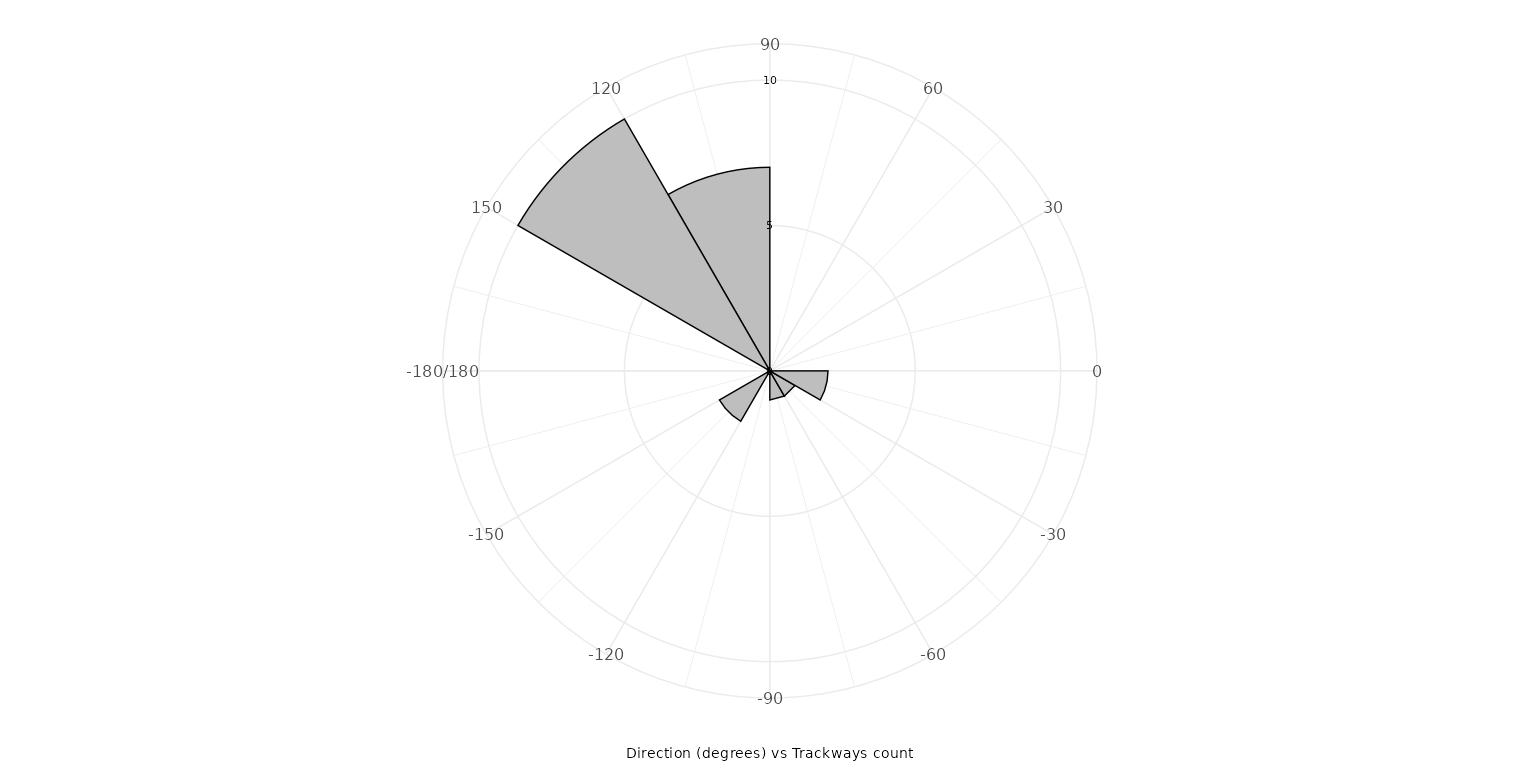
plot_direction(MountTom, plot_type = "polar_steps")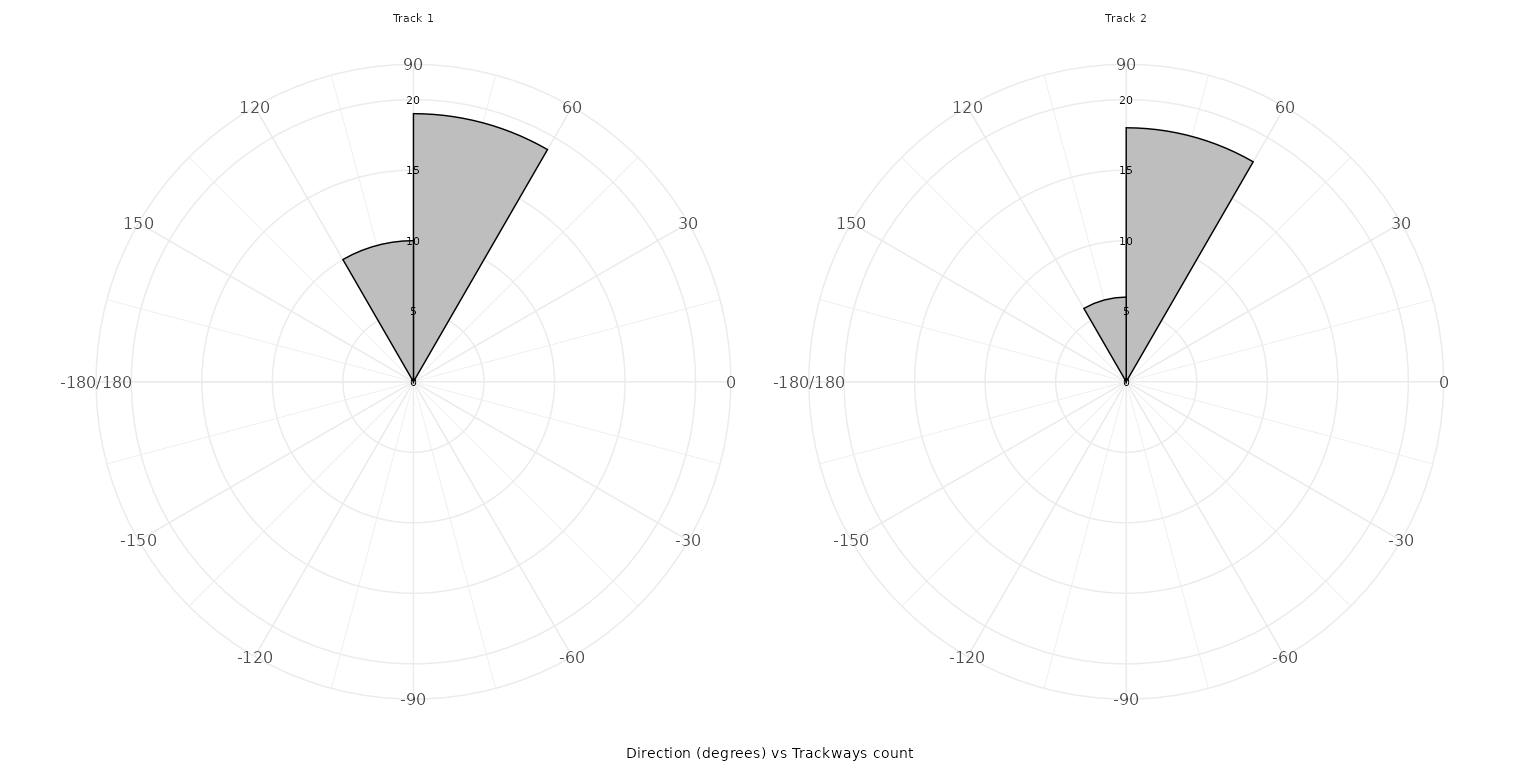
The polar_average option generates a
simplified polar plot by averaging step directions for each track,
providing a general overview of dominant movement trends.
plot_direction(PaluxyRiver, plot_type = "polar_average")
plot_direction(MountTom, plot_type = "polar_average")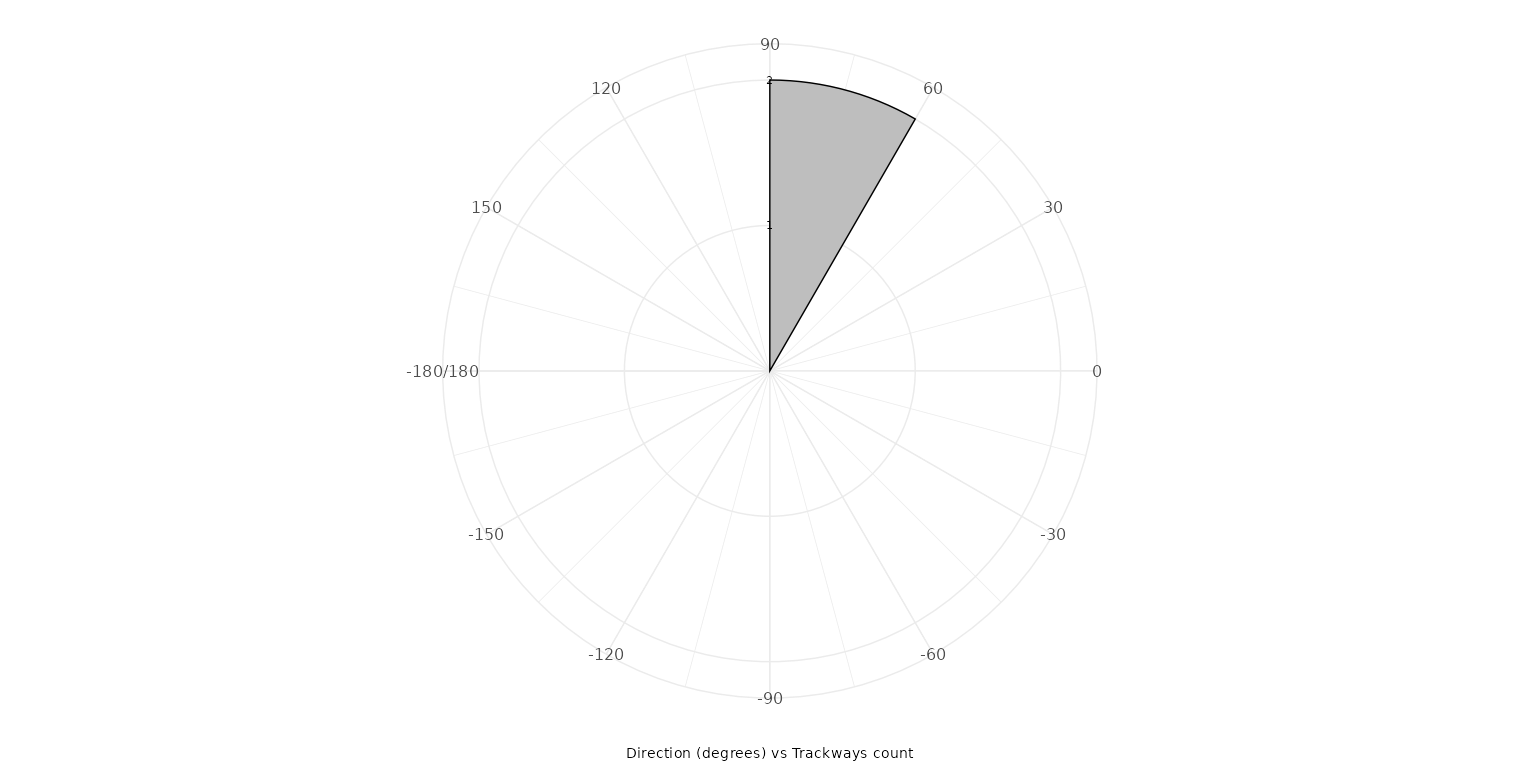
The faceted option displays individual
step directions separately for each track using faceted panels, allowing
detailed comparison of movement patterns across multiple tracks.
plot_direction(PaluxyRiver, plot_type = "faceted")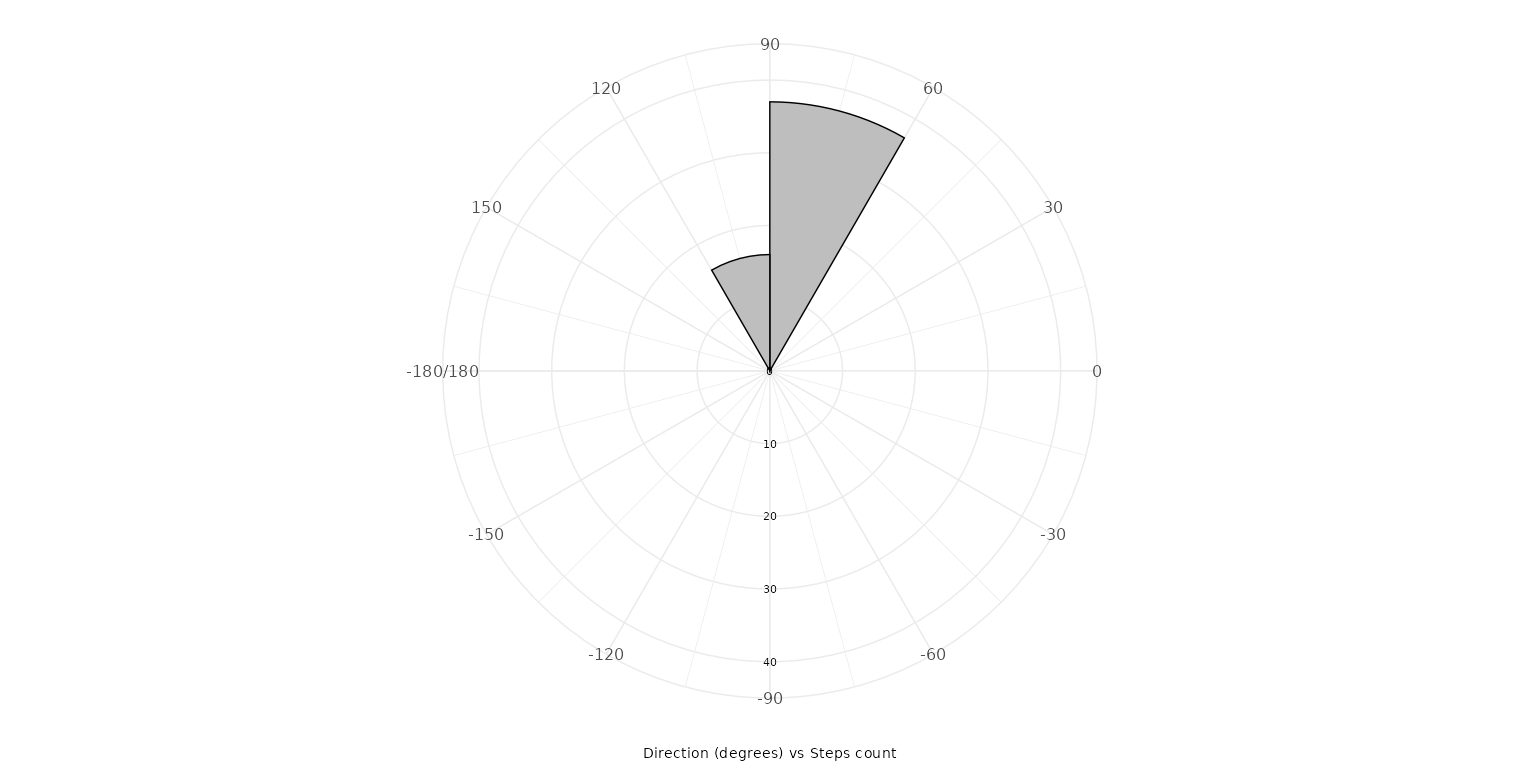
plot_direction(MountTom, plot_type = "faceted")
Customization options include setting custom breaks on the radial
axis with y_breaks_manual and adjusting
the position of y-axis labels with
y_labels_position for better
presentation.
plot_direction(PaluxyRiver, plot_type = "polar_average", y_breaks_manual = c(1, 2))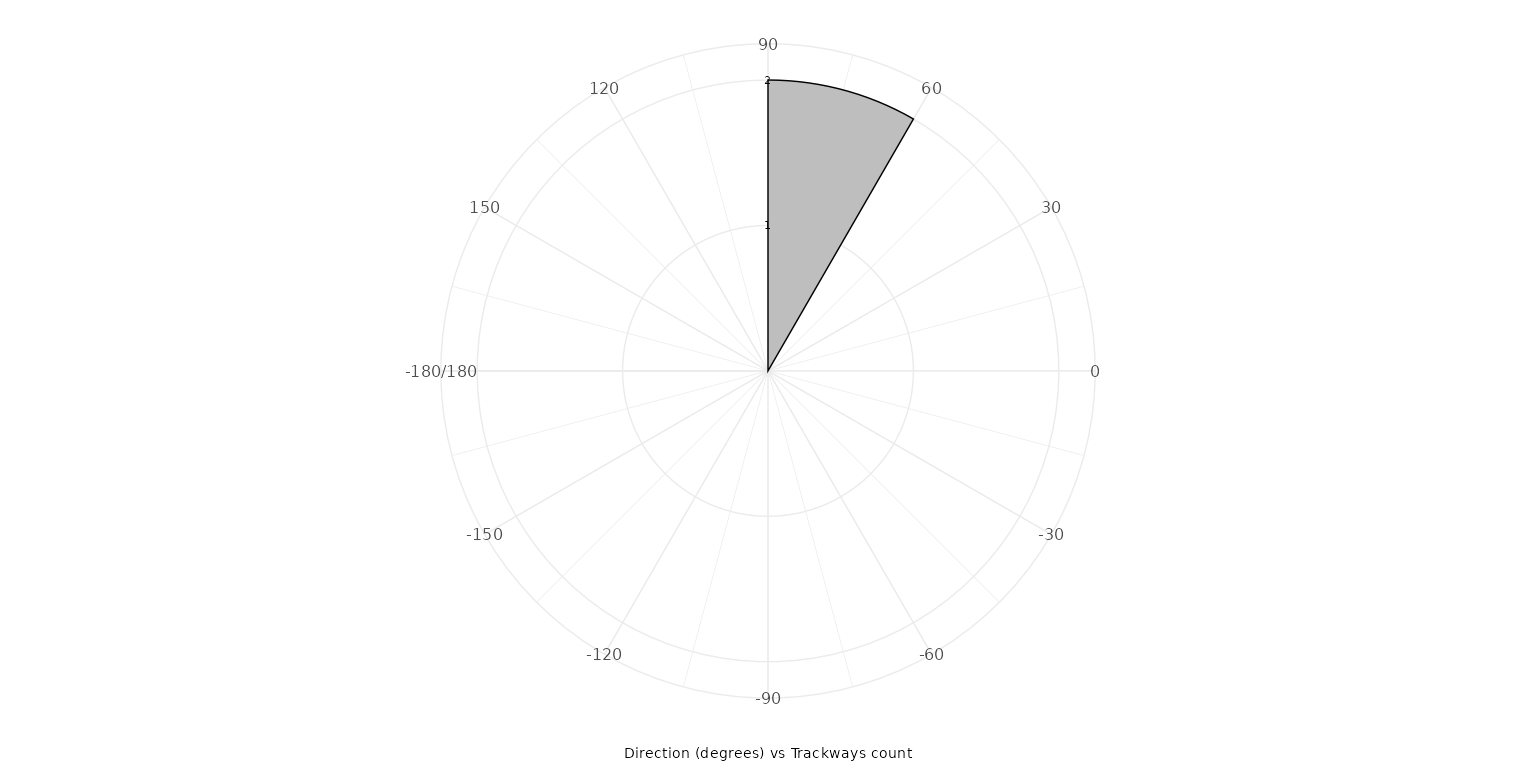
plot_direction(PaluxyRiver, plot_type = "polar_steps", y_labels_position = -90)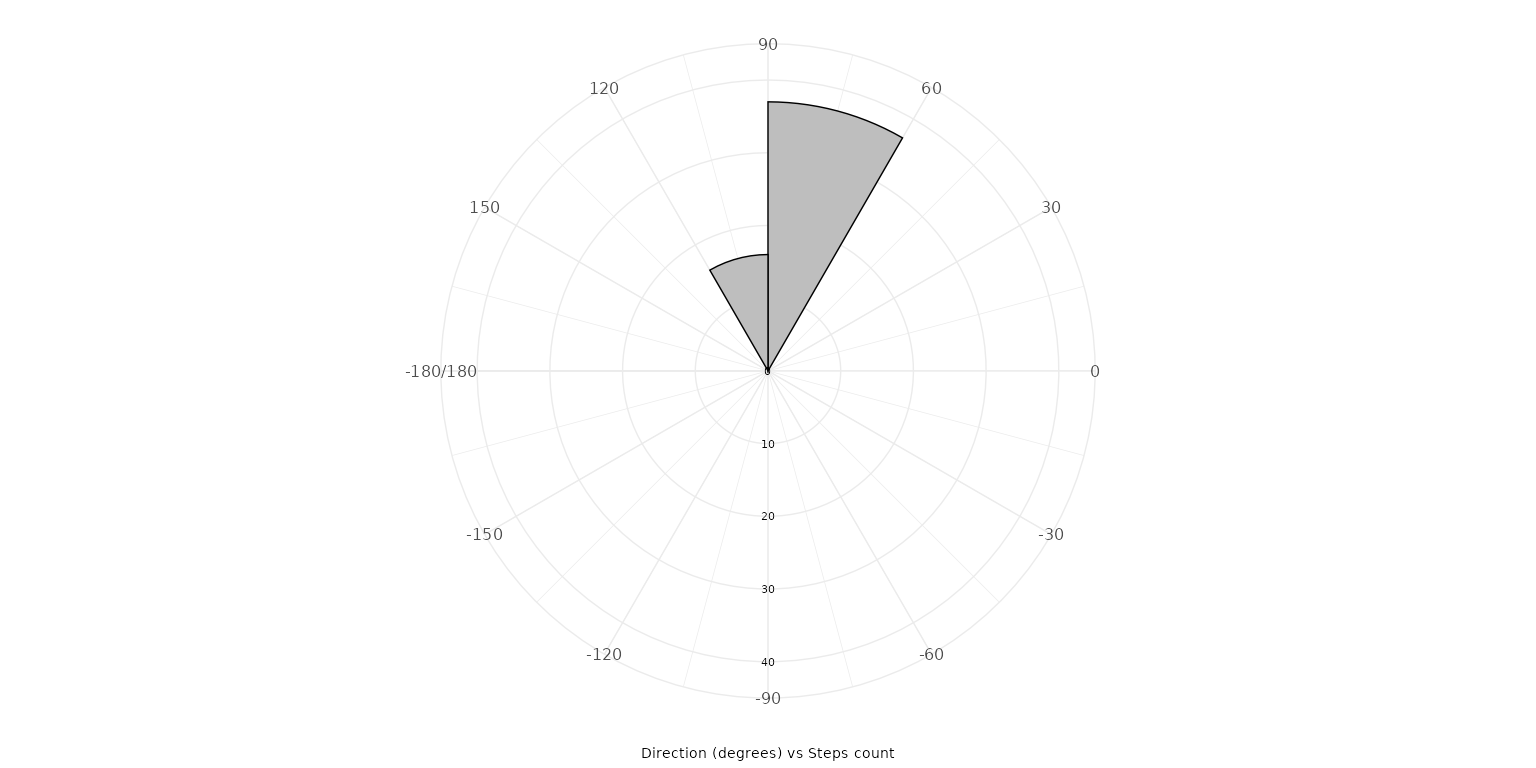
Testing for Differences in Velocity
The test_velocity() function evaluates
differences in velocities across different tracks
within a track R object. It provides three
statistical methods, which can be selected using the
analysis argument:: ANOVA,
Kruskal-Wallis test, and Generalized Linear
Models (GLM), allowing users to compare velocity data and
identify significant differences between tracks. The function also
includes diagnostic tests to check assumptions of
normality and homogeneity of variances
before proceeding with the analysis. When more than two tracks are
present, it performs pairwise comparisons to identify
specific differences between tracks.
The test_velocity() function requires
that each track contains more than three footprints to
be included in the analysis. This is necessary because statistical tests
for comparing mean velocities rely on having a sufficient number of data
points to provide meaningful results. When a track contains only three
or fewer footprints, the sample size is too small to accurately estimate
mean velocity and its variability, making statistical comparisons
unreliable. By setting this threshold, the function ensures that the
results are statistically robust and meaningful.
The function accepts a track velocity R
object, which is an output of the
velocity_track() function. This object
contains calculated velocities and other related
parameters for each track, including individual step
velocities, mean velocities, and
relative stride lengths. This information serves as the
input for the statistical comparisons performed by
test_velocity().
If "ANOVA" is selected, the function
checks for normality (using the Shapiro-Wilk
test) and homogeneity of variances (using
Levene’s test). If assumptions are violated, it issues
warnings suggesting the use of
"Kruskal-Wallis" or
"GLM" instead.
"ANOVA" compares mean velocities across
tracks, and if significant differences are detected, Tukey’s
HSD is used for post-hoc pairwise comparisons.
When "Kruskal-Wallis" is chosen, the
function performs a non-parametric test that compares
median velocities across tracks. If significant
differences are detected, Dunn’s test is used for
post-hoc pairwise comparisons. If
"GLM" is specified, the function uses a
Generalized Linear Model (GLM) with a Gaussian
family to compare mean velocities across
tracks. Pairwise comparisons are conducted using the
emmeans package, which computes
differences between group means and adjusts for multiple comparisons
using Tukey’s method. This approach is useful when the
data does not meet the assumptions of ANOVA but still
requires a parametric approach.
If the argument plot = TRUE is
specified, a boxplot of velocities by track is
generated for visual comparison of velocity
distributions across tracks. The boxplot allows the user to
visually assess differences in central tendency and
variability across tracks, complementing the
statistical analyses.
The function returns a list of results that includes:
normality_results, a matrix containing the
test statistic and p-value for the Shapiro-Wilk
normality test for each track;
homogeneity_test, the result of
Levene’s test, including the p-value for
testing homogeneity of variances across tracks;
ANOVA, if selected, containing the
ANOVA table and Tukey HSD post-hoc
results; Kruskal_Wallis, if selected,
containing the Kruskal-Wallis test result and
Dunn’s test post-hoc results;
GLM, if selected, providing a summary of
the GLM fit and pairwise comparisons from the
emmeans package; and finally, the
plot if requested, displaying a
boxplot of velocities by track.
Examples of Usage
The ANOVA method is suitable for comparing mean velocities when data meet the assumptions of normality and homogeneity of variances.
test_velocity(PaluxyRiver, velocity_paluxyriver_diff, analysis = "ANOVA")#> Warning in test_velocity(PaluxyRiver, velocity_paluxyriver_diff, analysis =
#> "ANOVA"): One or more tracks do not follow a normal distribution (p-value <=
#> 0.05). Assumptions for ANOVA are not met. Consider using 'Kruskal-Wallis' or
#> 'GLM'.
#> Warning in test_velocity(PaluxyRiver, velocity_paluxyriver_diff, analysis =
#> "ANOVA"): Homogeneity of variances assumption is violated (Levene's test
#> p-value <= 0.05). Assumptions for ANOVA are not met. Consider using
#> 'Kruskal-Wallis' or 'GLM'.
#> $normality_results
#> Trackway 1 Trackway 2
#> statistic.W 0.9586486 0.91134871
#> p_value 0.3043396 0.03773134
#>
#> $homogeneity_test
#> Levene's Test for Homogeneity of Variance (center = median)
#> Df F value Pr(>F)
#> group 1 18.698 7.121e-05 ***
#> 51
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> $ANOVA
#> $ANOVA$ANOVA
#> Df Sum Sq Mean Sq F value Pr(>F)
#> track 1 0.5086 0.5086 111.9 1.82e-14 ***
#> Residuals 51 0.2317 0.0045
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> $ANOVA$Tukey
#> Tukey multiple comparisons of means
#> 95% family-wise confidence level
#>
#> Fit: aov(formula = vel ~ track, data = M_analysis)
#>
#> $track
#> diff lwr upr p adj
#> Trackway 2-Trackway 1 0.1967992 0.1594567 0.2341416 0
test_velocity(MountTom, velocity_mounttom, analysis = "ANOVA")#> Warning in test_velocity(MountTom, velocity_mounttom, analysis = "ANOVA"): The
#> following tracks were removed from the analysis due to having 3 or fewer
#> footprints: Trackway 05, Trackway 06, Trackway 10, Trackway 11, Trackway 12,
#> Trackway 14, Trackway 17, Trackway 19, Trackway 20, Trackway 21, Trackway 22,
#> Trackway 23.
#> $normality_results
#> Trackway 01 Trackway 02 Trackway 03 Trackway 04 Trackway 07
#> statistic.W 0.9209702 0.9049639 0.8522781 0.9286605 0.9400514
#> p_value 0.4003329 0.2821994 0.2018271 0.5872649 0.6391828
#> Trackway 08 Trackway 09 Trackway 13 Trackway 15 Trackway 16
#> statistic.W 0.81516913 0.8697921 0.9420435 0.8148552 0.9692820
#> p_value 0.08011557 0.2655830 0.6804196 0.1064974 0.8923149
#> Trackway 18
#> statistic.W 0.8301712
#> p_value 0.1395325
#>
#> $homogeneity_test
#> Levene's Test for Homogeneity of Variance (center = median)
#> Df F value Pr(>F)
#> group 10 1.8159 0.07787 .
#> 58
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> $ANOVA
#> $ANOVA$ANOVA
#> Df Sum Sq Mean Sq F value Pr(>F)
#> track 10 7.750 0.7750 18.99 7.45e-15 ***
#> Residuals 58 2.367 0.0408
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> $ANOVA$Tukey
#> Tukey multiple comparisons of means
#> 95% family-wise confidence level
#>
#> Fit: aov(formula = vel ~ track, data = M_analysis)
#>
#> $track
#> diff lwr upr p adj
#> Trackway 02-Trackway 01 0.1647216595 -0.15432834 0.483771659 0.8140421
#> Trackway 03-Trackway 01 0.8203246689 0.44281962 1.197829720 0.0000001
#> Trackway 04-Trackway 01 -0.0496561965 -0.42716125 0.327848854 0.9999967
#> Trackway 07-Trackway 01 -0.2902954450 -0.63137424 0.050783352 0.1650949
#> Trackway 08-Trackway 01 0.0893925508 -0.26731619 0.446101295 0.9988034
#> Trackway 09-Trackway 01 0.5637709648 0.18626591 0.941276015 0.0002729
#> Trackway 13-Trackway 01 -0.5970292135 -0.97453426 -0.219524163 0.0000949
#> Trackway 15-Trackway 01 0.0425349739 -0.33497008 0.420040025 0.9999992
#> Trackway 16-Trackway 01 -0.1611827913 -0.49005200 0.167686421 0.8573485
#> Trackway 18-Trackway 01 -0.0007003399 -0.37820539 0.376804711 1.0000000
#> Trackway 03-Trackway 02 0.6556030094 0.27809796 1.033108060 0.0000140
#> Trackway 04-Trackway 02 -0.2143778560 -0.59188291 0.163127195 0.7130620
#> Trackway 07-Trackway 02 -0.4550171046 -0.79609590 -0.113938308 0.0017099
#> Trackway 08-Trackway 02 -0.0753291087 -0.43203785 0.281379635 0.9997305
#> Trackway 09-Trackway 02 0.3990493053 0.02154425 0.776554356 0.0298082
#> Trackway 13-Trackway 02 -0.7617508730 -1.13925592 -0.384245822 0.0000004
#> Trackway 15-Trackway 02 -0.1221866856 -0.49969174 0.255318365 0.9905449
#> Trackway 16-Trackway 02 -0.3259044509 -0.65477366 0.002964761 0.0541074
#> Trackway 18-Trackway 02 -0.1654219994 -0.54292705 0.212083051 0.9242930
#> Trackway 04-Trackway 03 -0.8699808655 -1.29803136 -0.441930373 0.0000003
#> Trackway 07-Trackway 03 -1.1106201140 -1.50691786 -0.714322364 0.0000000
#> Trackway 08-Trackway 03 -0.7309321181 -1.14075926 -0.321104973 0.0000078
#> Trackway 09-Trackway 03 -0.2565537042 -0.68460420 0.171496788 0.6442769
#> Trackway 13-Trackway 03 -1.4173538824 -1.84540437 -0.989303390 0.0000000
#> Trackway 15-Trackway 03 -0.7777896950 -1.20584019 -0.349739202 0.0000051
#> Trackway 16-Trackway 03 -0.9815074603 -1.36734696 -0.595667960 0.0000000
#> Trackway 18-Trackway 03 -0.8210250088 -1.24907550 -0.392974516 0.0000014
#> Trackway 07-Trackway 04 -0.2406392485 -0.63693700 0.155658501 0.6265904
#> Trackway 08-Trackway 04 0.1390487473 -0.27077840 0.548875892 0.9865339
#> Trackway 09-Trackway 04 0.6134271613 0.18537667 1.041477654 0.0005536
#> Trackway 13-Trackway 04 -0.5473730170 -0.97542351 -0.119322524 0.0031439
#> Trackway 15-Trackway 04 0.0921911704 -0.33585932 0.520241663 0.9996790
#> Trackway 16-Trackway 04 -0.1115265948 -0.49736609 0.274312905 0.9961010
#> Trackway 18-Trackway 04 0.0489558567 -0.37909464 0.477006349 0.9999991
#> Trackway 08-Trackway 07 0.3796879959 0.00314720 0.756228792 0.0464388
#> Trackway 09-Trackway 07 0.8540664098 0.45776866 1.250364160 0.0000001
#> Trackway 13-Trackway 07 -0.3067337684 -0.70303152 0.089563981 0.2762333
#> Trackway 15-Trackway 07 0.3328304190 -0.06346733 0.729128169 0.1788423
#> Trackway 16-Trackway 07 0.1291126537 -0.22116838 0.479393686 0.9755347
#> Trackway 18-Trackway 07 0.2895951052 -0.10670264 0.685892855 0.3557291
#> Trackway 09-Trackway 08 0.4743784140 0.06455127 0.884205559 0.0112278
#> Trackway 13-Trackway 08 -0.6864217643 -1.09624891 -0.276594619 0.0000303
#> Trackway 15-Trackway 08 -0.0468575769 -0.45668472 0.362969568 0.9999991
#> Trackway 16-Trackway 08 -0.2505753422 -0.61609304 0.114942351 0.4499019
#> Trackway 18-Trackway 08 -0.0900928907 -0.49992004 0.319734254 0.9996153
#> Trackway 13-Trackway 09 -1.1608001783 -1.58885067 -0.732749686 0.0000000
#> Trackway 15-Trackway 09 -0.5212359909 -0.94928648 -0.093185498 0.0060381
#> Trackway 16-Trackway 09 -0.7249537561 -1.11079326 -0.339114256 0.0000023
#> Trackway 18-Trackway 09 -0.5644713046 -0.99252180 -0.136420812 0.0020281
#> Trackway 15-Trackway 13 0.6395641874 0.21151369 1.067614680 0.0002706
#> Trackway 16-Trackway 13 0.4358464222 0.05000692 0.821685922 0.0148416
#> Trackway 18-Trackway 13 0.5963288736 0.16827838 1.024379366 0.0008771
#> Trackway 16-Trackway 15 -0.2037177653 -0.58955727 0.182121735 0.7928071
#> Trackway 18-Trackway 15 -0.0432353138 -0.47128581 0.384815179 0.9999997
#> Trackway 18-Trackway 16 0.1604824515 -0.22535705 0.546321951 0.9451623The Kruskal-Wallis test is a non-parametric method that compares median velocities, useful when normality or homogeneity of variances cannot be assumed.
test_velocity(PaluxyRiver, velocity_paluxyriver_diff, analysis = "Kruskal-Wallis")#> Warning in test_velocity(PaluxyRiver, velocity_paluxyriver_diff, analysis =
#> "Kruskal-Wallis"): One or more tracks do not follow a normal distribution
#> (p-value <= 0.05). Assumptions for ANOVA are not met. Consider using
#> 'Kruskal-Wallis' or 'GLM'.
#> Warning in test_velocity(PaluxyRiver, velocity_paluxyriver_diff, analysis =
#> "Kruskal-Wallis"): Homogeneity of variances assumption is violated (Levene's
#> test p-value <= 0.05). Assumptions for ANOVA are not met. Consider using
#> 'Kruskal-Wallis' or 'GLM'.
#> Kruskal-Wallis rank sum test
#>
#> data: x and group
#> Kruskal-Wallis chi-squared = 38.6698, df = 1, p-value = 0
#>
#>
#> Comparison of x by group
#> (No adjustment)
#> Col Mean-|
#> Row Mean | Trackway
#> ---------+-----------
#> Trackway | -6.218503
#> | 0.0000*
#>
#> alpha = 0.05
#> Reject Ho if p <= alpha/2
#> $normality_results
#> Trackway 1 Trackway 2
#> statistic.W 0.9586486 0.91134871
#> p_value 0.3043396 0.03773134
#>
#> $homogeneity_test
#> Levene's Test for Homogeneity of Variance (center = median)
#> Df F value Pr(>F)
#> group 1 18.698 7.121e-05 ***
#> 51
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> $Kruskal_Wallis
#> $Kruskal_Wallis$Kruskal_Wallis
#>
#> Kruskal-Wallis rank sum test
#>
#> data: vel by track
#> Kruskal-Wallis chi-squared = 38.67, df = 1, p-value = 5.019e-10
#>
#>
#> $Kruskal_Wallis$Dunn
#> $Kruskal_Wallis$Dunn$chi2
#> [1] 38.66978
#>
#> $Kruskal_Wallis$Dunn$Z
#> [1] -6.218503
#>
#> $Kruskal_Wallis$Dunn$P
#> [1] 2.509595e-10
#>
#> $Kruskal_Wallis$Dunn$P.adjusted
#> [1] 2.509595e-10
#>
#> $Kruskal_Wallis$Dunn$comparisons
#> [1] "Trackway 1 - Trackway 2"
test_velocity(MountTom, velocity_mounttom, analysis = "Kruskal-Wallis")#> Warning in test_velocity(MountTom, velocity_mounttom, analysis =
#> "Kruskal-Wallis"): The following tracks were removed from the analysis due to
#> having 3 or fewer footprints: Trackway 05, Trackway 06, Trackway 10, Trackway
#> 11, Trackway 12, Trackway 14, Trackway 17, Trackway 19, Trackway 20, Trackway
#> 21, Trackway 22, Trackway 23.
#> Kruskal-Wallis rank sum test
#>
#> data: x and group
#> Kruskal-Wallis chi-squared = 47.0791, df = 10, p-value = 0
#>
#>
#> Comparison of x by group
#> (No adjustment)
#> Col Mean-|
#> Row Mean | Trackway Trackway Trackway Trackway Trackway Trackway
#> ---------+------------------------------------------------------------------
#> Trackway | -1.421706
#> | 0.0776
#> |
#> Trackway | -2.691099 -1.489538
#> | 0.0036* 0.0682
#> |
#> Trackway | 0.490554 1.692115 2.805954
#> | 0.3119 0.0453 0.0025*
#> |
#> Trackway | 2.038004 3.367888 4.317520 1.286742
#> | 0.0208* 0.0004* 0.0000* 0.0991
#> |
#> Trackway | -0.704116 0.567496 1.866004 -1.064720 -2.513099
#> | 0.2407 0.2852 0.0310 0.1435 0.0060*
#> |
#> Trackway | -2.101242 -0.899681 0.520205 -2.285749 -3.755634 -1.322667
#> | 0.0178* 0.1841 0.3015 0.0111* 0.0001* 0.0930
#> |
#> Trackway | 2.778485 3.980046 4.823720 2.017765 0.892692 3.172207
#> | 0.0027* 0.0000* 0.0000* 0.0218* 0.1860 0.0008*
#> |
#> Trackway | -0.349544 0.852015 2.065056 -0.740898 -2.087004 0.290877
#> | 0.3633 0.1971 0.0195* 0.2294 0.0184* 0.3856
#> |
#> Trackway | 1.476147 2.855404 3.891159 0.778231 -0.598549 2.015289
#> | 0.0700 0.0021* 0.0000* 0.2182 0.2747 0.0219*
#> |
#> Trackway | 0.061567 1.263128 2.427623 -0.378331 -1.695386 0.669566
#> | 0.4755 0.1033 0.0076* 0.3526 0.0450 0.2516
#> Col Mean-|
#> Row Mean | Trackway Trackway Trackway Trackway
#> ---------+--------------------------------------------
#> Trackway | 4.303515
#> | 0.0000*
#> |
#> Trackway | 1.544851 -2.758663
#> | 0.0612 0.0029*
#> |
#> Trackway | 3.314043 -1.460277 1.600184
#> | 0.0005* 0.0721 0.0548
#> |
#> Trackway | 1.907418 -2.396096 0.362567 -1.197952
#> | 0.0282 0.0083* 0.3585 0.1155
#>
#> alpha = 0.05
#> Reject Ho if p <= alpha/2
#> $normality_results
#> Trackway 01 Trackway 02 Trackway 03 Trackway 04 Trackway 07
#> statistic.W 0.9209702 0.9049639 0.8522781 0.9286605 0.9400514
#> p_value 0.4003329 0.2821994 0.2018271 0.5872649 0.6391828
#> Trackway 08 Trackway 09 Trackway 13 Trackway 15 Trackway 16
#> statistic.W 0.81516913 0.8697921 0.9420435 0.8148552 0.9692820
#> p_value 0.08011557 0.2655830 0.6804196 0.1064974 0.8923149
#> Trackway 18
#> statistic.W 0.8301712
#> p_value 0.1395325
#>
#> $homogeneity_test
#> Levene's Test for Homogeneity of Variance (center = median)
#> Df F value Pr(>F)
#> group 10 1.8159 0.07787 .
#> 58
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> $Kruskal_Wallis
#> $Kruskal_Wallis$Kruskal_Wallis
#>
#> Kruskal-Wallis rank sum test
#>
#> data: vel by track
#> Kruskal-Wallis chi-squared = 47.079, df = 10, p-value = 9.135e-07
#>
#>
#> $Kruskal_Wallis$Dunn
#> $Kruskal_Wallis$Dunn$chi2
#> [1] 47.07915
#>
#> $Kruskal_Wallis$Dunn$Z
#> [1] -1.42170606 -2.69109927 -1.48953834 0.49055463 1.69211556 2.80595499
#> [7] 2.03800443 3.36788868 4.31752052 1.28674273 -0.70411605 0.56749651
#> [13] 1.86600430 -1.06472010 -2.51309940 -2.10124209 -0.89968116 0.52020514
#> [19] -2.28574985 -3.75563475 -1.32266775 2.77848552 3.98004645 4.82372037
#> [25] 2.01776539 0.89269297 3.17220731 4.30351524 -0.34954500 0.85201593
#> [31] 2.06505676 -0.74089823 -2.08700428 0.29087714 1.54485162 -2.75866361
#> [37] 1.47614746 2.85540494 3.89115946 0.77823189 -0.59854981 2.01528904
#> [43] 3.31404367 -1.46027782 1.60018468 0.06156758 1.26312851 2.42762398
#> [49] -0.37833101 -1.69538693 0.66956625 1.90741884 -2.39609639 0.36256722
#> [55] -1.19795246
#>
#> $Kruskal_Wallis$Dunn$P
#> [1] 7.755580e-02 3.560850e-03 6.817283e-02 3.118707e-01 4.531197e-02
#> [6] 2.508385e-03 2.077474e-02 3.787309e-04 7.889587e-06 9.909199e-02
#> [11] 2.406803e-01 2.851884e-01 3.102038e-02 1.435013e-01 5.983780e-03
#> [16] 1.780986e-02 1.841450e-01 3.014603e-01 1.113445e-02 8.645135e-05
#> [21] 9.297295e-02 2.730647e-03 3.445090e-05 7.045246e-07 2.180785e-02
#> [26] 1.860108e-01 7.564248e-04 8.405464e-06 3.633401e-01 1.971026e-01
#> [31] 1.945881e-02 2.293776e-01 1.844387e-02 3.855726e-01 6.119108e-02
#> [36] 2.901912e-03 6.995215e-02 2.149099e-03 4.988317e-05 2.182162e-01
#> [41] 2.747366e-01 2.193719e-02 4.597857e-04 7.210687e-02 5.477881e-02
#> [46] 4.754536e-01 1.032715e-01 7.599046e-03 3.525924e-01 4.500102e-02
#> [51] 2.515672e-01 2.823319e-02 8.285366e-03 3.584641e-01 1.154678e-01
#>
#> $Kruskal_Wallis$Dunn$P.adjusted
#> [1] 7.755580e-02 3.560850e-03 6.817283e-02 3.118707e-01 4.531197e-02
#> [6] 2.508385e-03 2.077474e-02 3.787309e-04 7.889587e-06 9.909199e-02
#> [11] 2.406803e-01 2.851884e-01 3.102038e-02 1.435013e-01 5.983780e-03
#> [16] 1.780986e-02 1.841450e-01 3.014603e-01 1.113445e-02 8.645135e-05
#> [21] 9.297295e-02 2.730647e-03 3.445090e-05 7.045246e-07 2.180785e-02
#> [26] 1.860108e-01 7.564248e-04 8.405464e-06 3.633401e-01 1.971026e-01
#> [31] 1.945881e-02 2.293776e-01 1.844387e-02 3.855726e-01 6.119108e-02
#> [36] 2.901912e-03 6.995215e-02 2.149099e-03 4.988317e-05 2.182162e-01
#> [41] 2.747366e-01 2.193719e-02 4.597857e-04 7.210687e-02 5.477881e-02
#> [46] 4.754536e-01 1.032715e-01 7.599046e-03 3.525924e-01 4.500102e-02
#> [51] 2.515672e-01 2.823319e-02 8.285366e-03 3.584641e-01 1.154678e-01
#>
#> $Kruskal_Wallis$Dunn$comparisons
#> [1] "Trackway 01 - Trackway 02" "Trackway 01 - Trackway 03"
#> [3] "Trackway 02 - Trackway 03" "Trackway 01 - Trackway 04"
#> [5] "Trackway 02 - Trackway 04" "Trackway 03 - Trackway 04"
#> [7] "Trackway 01 - Trackway 07" "Trackway 02 - Trackway 07"
#> [9] "Trackway 03 - Trackway 07" "Trackway 04 - Trackway 07"
#> [11] "Trackway 01 - Trackway 08" "Trackway 02 - Trackway 08"
#> [13] "Trackway 03 - Trackway 08" "Trackway 04 - Trackway 08"
#> [15] "Trackway 07 - Trackway 08" "Trackway 01 - Trackway 09"
#> [17] "Trackway 02 - Trackway 09" "Trackway 03 - Trackway 09"
#> [19] "Trackway 04 - Trackway 09" "Trackway 07 - Trackway 09"
#> [21] "Trackway 08 - Trackway 09" "Trackway 01 - Trackway 13"
#> [23] "Trackway 02 - Trackway 13" "Trackway 03 - Trackway 13"
#> [25] "Trackway 04 - Trackway 13" "Trackway 07 - Trackway 13"
#> [27] "Trackway 08 - Trackway 13" "Trackway 09 - Trackway 13"
#> [29] "Trackway 01 - Trackway 15" "Trackway 02 - Trackway 15"
#> [31] "Trackway 03 - Trackway 15" "Trackway 04 - Trackway 15"
#> [33] "Trackway 07 - Trackway 15" "Trackway 08 - Trackway 15"
#> [35] "Trackway 09 - Trackway 15" "Trackway 13 - Trackway 15"
#> [37] "Trackway 01 - Trackway 16" "Trackway 02 - Trackway 16"
#> [39] "Trackway 03 - Trackway 16" "Trackway 04 - Trackway 16"
#> [41] "Trackway 07 - Trackway 16" "Trackway 08 - Trackway 16"
#> [43] "Trackway 09 - Trackway 16" "Trackway 13 - Trackway 16"
#> [45] "Trackway 15 - Trackway 16" "Trackway 01 - Trackway 18"
#> [47] "Trackway 02 - Trackway 18" "Trackway 03 - Trackway 18"
#> [49] "Trackway 04 - Trackway 18" "Trackway 07 - Trackway 18"
#> [51] "Trackway 08 - Trackway 18" "Trackway 09 - Trackway 18"
#> [53] "Trackway 13 - Trackway 18" "Trackway 15 - Trackway 18"
#> [55] "Trackway 16 - Trackway 18"The GLM approach offers a flexible alternative when
data do not meet the assumptions required for ANOVA. This method fits a
linear model with a Gaussian family and performs pairwise comparisons
using emmeans.
test_velocity(PaluxyRiver, velocity_paluxyriver_diff, analysis = "GLM")#> Warning in test_velocity(PaluxyRiver, velocity_paluxyriver_diff, analysis =
#> "GLM"): One or more tracks do not follow a normal distribution (p-value <=
#> 0.05). Assumptions for ANOVA are not met. Consider using 'Kruskal-Wallis' or
#> 'GLM'.
#> Warning in test_velocity(PaluxyRiver, velocity_paluxyriver_diff, analysis =
#> "GLM"): Homogeneity of variances assumption is violated (Levene's test p-value
#> <= 0.05). Assumptions for ANOVA are not met. Consider using 'Kruskal-Wallis' or
#> 'GLM'.
#> $normality_results
#> Trackway 1 Trackway 2
#> statistic.W 0.9586486 0.91134871
#> p_value 0.3043396 0.03773134
#>
#> $homogeneity_test
#> Levene's Test for Homogeneity of Variance (center = median)
#> Df F value Pr(>F)
#> group 1 18.698 7.121e-05 ***
#> 51
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> $GLM
#> $GLM$GLM
#>
#> Call:
#> glm(formula = vel ~ track, family = gaussian(), data = M_analysis)
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 0.20764 0.01252 16.59 < 2e-16 ***
#> trackTrackway 2 0.19680 0.01860 10.58 1.82e-14 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> (Dispersion parameter for gaussian family taken to be 0.004543515)
#>
#> Null deviance: 0.74032 on 52 degrees of freedom
#> Residual deviance: 0.23172 on 51 degrees of freedom
#> AIC: -131.52
#>
#> Number of Fisher Scoring iterations: 2
#>
#>
#> $GLM$pairwise_results
#> $emmeans
#> track emmean SE df lower.CL upper.CL
#> Trackway 1 0.208 0.0125 51 0.183 0.233
#> Trackway 2 0.404 0.0138 51 0.377 0.432
#>
#> Confidence level used: 0.95
#>
#> $contrasts
#> contrast estimate SE df t.ratio p.value
#> Trackway 1 - Trackway 2 -0.197 0.0186 51 -10.580 <0.0001
test_velocity(MountTom, velocity_mounttom, analysis = "GLM")#> Warning in test_velocity(MountTom, velocity_mounttom, analysis = "GLM"): The
#> following tracks were removed from the analysis due to having 3 or fewer
#> footprints: Trackway 05, Trackway 06, Trackway 10, Trackway 11, Trackway 12,
#> Trackway 14, Trackway 17, Trackway 19, Trackway 20, Trackway 21, Trackway 22,
#> Trackway 23.
#> $normality_results
#> Trackway 01 Trackway 02 Trackway 03 Trackway 04 Trackway 07
#> statistic.W 0.9209702 0.9049639 0.8522781 0.9286605 0.9400514
#> p_value 0.4003329 0.2821994 0.2018271 0.5872649 0.6391828
#> Trackway 08 Trackway 09 Trackway 13 Trackway 15 Trackway 16
#> statistic.W 0.81516913 0.8697921 0.9420435 0.8148552 0.9692820
#> p_value 0.08011557 0.2655830 0.6804196 0.1064974 0.8923149
#> Trackway 18
#> statistic.W 0.8301712
#> p_value 0.1395325
#>
#> $homogeneity_test
#> Levene's Test for Homogeneity of Variance (center = median)
#> Df F value Pr(>F)
#> group 10 1.8159 0.07787 .
#> 58
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> $GLM
#> $GLM$GLM
#>
#> Call:
#> glm(formula = vel ~ track, family = gaussian(), data = M_analysis)
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 1.3958203 0.0673391 20.728 < 2e-16 ***
#> trackTrackway 02 0.1647217 0.0952318 1.730 0.08900 .
#> trackTrackway 03 0.8203247 0.1126798 7.280 9.91e-10 ***
#> trackTrackway 04 -0.0496562 0.1126798 -0.441 0.66108
#> trackTrackway 07 -0.2902954 0.1018071 -2.851 0.00602 **
#> trackTrackway 08 0.0893926 0.1064724 0.840 0.40459
#> trackTrackway 09 0.5637710 0.1126798 5.003 5.55e-06 ***
#> trackTrackway 13 -0.5970292 0.1126798 -5.298 1.89e-06 ***
#> trackTrackway 15 0.0425350 0.1126798 0.377 0.70719
#> trackTrackway 16 -0.1611828 0.0981627 -1.642 0.10600
#> trackTrackway 18 -0.0007003 0.1126798 -0.006 0.99506
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> (Dispersion parameter for gaussian family taken to be 0.04081095)
#>
#> Null deviance: 10.117 on 68 degrees of freedom
#> Residual deviance: 2.367 on 58 degrees of freedom
#> AIC: -12.887
#>
#> Number of Fisher Scoring iterations: 2
#>
#>
#> $GLM$pairwise_results
#> $emmeans
#> track emmean SE df lower.CL upper.CL
#> Trackway 01 1.396 0.0673 58 1.261 1.53
#> Trackway 02 1.561 0.0673 58 1.426 1.70
#> Trackway 03 2.216 0.0903 58 2.035 2.40
#> Trackway 04 1.346 0.0903 58 1.165 1.53
#> Trackway 07 1.106 0.0764 58 0.953 1.26
#> Trackway 08 1.485 0.0825 58 1.320 1.65
#> Trackway 09 1.960 0.0903 58 1.779 2.14
#> Trackway 13 0.799 0.0903 58 0.618 0.98
#> Trackway 15 1.438 0.0903 58 1.258 1.62
#> Trackway 16 1.235 0.0714 58 1.092 1.38
#> Trackway 18 1.395 0.0903 58 1.214 1.58
#>
#> Confidence level used: 0.95
#>
#> $contrasts
#> contrast estimate SE df t.ratio p.value
#> Trackway 01 - Trackway 02 -0.1647 0.0952 58 -1.730 0.8140
#> Trackway 01 - Trackway 03 -0.8203 0.1130 58 -7.280 <0.0001
#> Trackway 01 - Trackway 04 0.0497 0.1130 58 0.441 1.0000
#> Trackway 01 - Trackway 07 0.2903 0.1020 58 2.851 0.1651
#> Trackway 01 - Trackway 08 -0.0894 0.1060 58 -0.840 0.9988
#> Trackway 01 - Trackway 09 -0.5638 0.1130 58 -5.003 0.0003
#> Trackway 01 - Trackway 13 0.5970 0.1130 58 5.298 <0.0001
#> Trackway 01 - Trackway 15 -0.0425 0.1130 58 -0.377 1.0000
#> Trackway 01 - Trackway 16 0.1612 0.0982 58 1.642 0.8573
#> Trackway 01 - Trackway 18 0.0007 0.1130 58 0.006 1.0000
#> Trackway 02 - Trackway 03 -0.6556 0.1130 58 -5.818 <0.0001
#> Trackway 02 - Trackway 04 0.2144 0.1130 58 1.903 0.7131
#> Trackway 02 - Trackway 07 0.4550 0.1020 58 4.469 0.0017
#> Trackway 02 - Trackway 08 0.0753 0.1060 58 0.707 0.9997
#> Trackway 02 - Trackway 09 -0.3990 0.1130 58 -3.541 0.0298
#> Trackway 02 - Trackway 13 0.7618 0.1130 58 6.760 <0.0001
#> Trackway 02 - Trackway 15 0.1222 0.1130 58 1.084 0.9905
#> Trackway 02 - Trackway 16 0.3259 0.0982 58 3.320 0.0541
#> Trackway 02 - Trackway 18 0.1654 0.1130 58 1.468 0.9243
#> Trackway 03 - Trackway 04 0.8700 0.1280 58 6.809 <0.0001
#> Trackway 03 - Trackway 07 1.1106 0.1180 58 9.389 <0.0001
#> Trackway 03 - Trackway 08 0.7309 0.1220 58 5.975 <0.0001
#> Trackway 03 - Trackway 09 0.2566 0.1280 58 2.008 0.6443
#> Trackway 03 - Trackway 13 1.4174 0.1280 58 11.093 <0.0001
#> Trackway 03 - Trackway 15 0.7778 0.1280 58 6.088 <0.0001
#> Trackway 03 - Trackway 16 0.9815 0.1150 58 8.522 <0.0001
#> Trackway 03 - Trackway 18 0.8210 0.1280 58 6.426 <0.0001
#> Trackway 04 - Trackway 07 0.2406 0.1180 58 2.034 0.6266
#> Trackway 04 - Trackway 08 -0.1390 0.1220 58 -1.137 0.9865
#> Trackway 04 - Trackway 09 -0.6134 0.1280 58 -4.801 0.0006
#> Trackway 04 - Trackway 13 0.5474 0.1280 58 4.284 0.0031
#> Trackway 04 - Trackway 15 -0.0922 0.1280 58 -0.722 0.9997
#> Trackway 04 - Trackway 16 0.1115 0.1150 58 0.968 0.9961
#> Trackway 04 - Trackway 18 -0.0490 0.1280 58 -0.383 1.0000
#> Trackway 07 - Trackway 08 -0.3797 0.1120 58 -3.378 0.0464
#> Trackway 07 - Trackway 09 -0.8541 0.1180 58 -7.220 <0.0001
#> Trackway 07 - Trackway 13 0.3067 0.1180 58 2.593 0.2762
#> Trackway 07 - Trackway 15 -0.3328 0.1180 58 -2.814 0.1788
#> Trackway 07 - Trackway 16 -0.1291 0.1050 58 -1.235 0.9755
#> Trackway 07 - Trackway 18 -0.2896 0.1180 58 -2.448 0.3557
#> Trackway 08 - Trackway 09 -0.4744 0.1220 58 -3.878 0.0112
#> Trackway 08 - Trackway 13 0.6864 0.1220 58 5.611 <0.0001
#> Trackway 08 - Trackway 15 0.0469 0.1220 58 0.383 1.0000
#> Trackway 08 - Trackway 16 0.2506 0.1090 58 2.297 0.4499
#> Trackway 08 - Trackway 18 0.0901 0.1220 58 0.736 0.9996
#> Trackway 09 - Trackway 13 1.1608 0.1280 58 9.085 <0.0001
#> Trackway 09 - Trackway 15 0.5212 0.1280 58 4.080 0.0060
#> Trackway 09 - Trackway 16 0.7250 0.1150 58 6.295 <0.0001
#> Trackway 09 - Trackway 18 0.5645 0.1280 58 4.418 0.0020
#> Trackway 13 - Trackway 15 -0.6396 0.1280 58 -5.006 0.0003
#> Trackway 13 - Trackway 16 -0.4358 0.1150 58 -3.784 0.0148
#> Trackway 13 - Trackway 18 -0.5963 0.1280 58 -4.667 0.0009
#> Trackway 15 - Trackway 16 0.2037 0.1150 58 1.769 0.7928
#> Trackway 15 - Trackway 18 0.0432 0.1280 58 0.338 1.0000
#> Trackway 16 - Trackway 18 -0.1605 0.1150 58 -1.393 0.9452
#>
#> P value adjustment: tukey method for comparing a family of 11 estimatesTesting for Acceleration, Deceleration, or Steady Movement along Trajectories
The mode_velocity() function evaluates
whether a track maker is accelerating,
decelerating, or maintaining a steady
speed along its trajectory by applying Spearman’s rank
correlation test. This test is particularly suitable for
analyzing trends in velocity because it does not assume normality or
linearity in the relationship between step number and velocity. Instead,
it detects monotonic relationships based on ranks,
making it robust to outliers and effective for
identifying general trends.
The function accepts a track velocity R
object and processes each trajectory separately. For each
trajectory, the function calculates the Spearman correlation
coefficient and its associated p-value, comparing
velocity values to their corresponding step
numbers. If the p-value is less than
0.05, the trend is classified as
“acceleration” if the correlation coefficient is
positive or “deceleration” if it is negative. If the
p-value is greater than or equal to 0.05, the
trend is labeled as “steady,” indicating no significant
monotonic relationship between velocity and step
number. This approach allows the detection of gradual changes
in velocity over the course of a track, which may reflect shifts in
locomotor performance or behavior.
Trajectories with fewer than three steps are considered insufficient for reliable statistical analysis, and the function returns a message indicating that the data is inadequate for correlation analysis. This is because the calculation of a meaningful correlation requires a minimum of three data points.
The mode_velocity() function provides a
straightforward way to classify velocity trends based
on statistical significance, making it a useful tool for examining how
track makers modulate their speed along their paths.
However, it only identifies monotonic trends and may
not detect more complex, non-monotonic changes in
speed. Furthermore, the classification is
qualitative, providing information about the general
nature of the trend rather than quantifying the rate of change.
This approach draws from established non-parametric statistical techniques for measuring association between variables. The robustness of the method to non-normal data and its resistance to outliers makes it well-suited for paleontological and biomechanical applications where data quality and quantity can be limited.
Examples of Usage
The velocity_paluxyriver_diff object
contains calculated velocities for the PaluxyRiver
dataset with different methods applied to the sauropod (Method
A) and theropod (Method B).
mode_velocity(velocity_paluxyriver_diff)#> $Track_1
#> $Track_1$correlation
#>
#> Spearman's rank correlation rho
#>
#> data: velocity and steps
#> S = 3178, p-value = 0.5088
#> alternative hypothesis: true rho is not equal to 0
#> sample estimates:
#> rho
#> 0.1302682
#>
#>
#> $Track_1$trend
#> [1] "Steady"
#>
#>
#> $Track_2
#> $Track_2$correlation
#>
#> Spearman's rank correlation rho
#>
#> data: velocity and steps
#> S = 1426, p-value = 0.1711
#> alternative hypothesis: true rho is not equal to 0
#> sample estimates:
#> rho
#> 0.2954545
#>
#>
#> $Track_2$trend
#> [1] "Steady"The velocity_mounttom object contains
calculated velocities for the MountTom dataset.
mode_velocity(velocity_mounttom)#> $Track_01
#> $Track_01$correlation
#>
#> Spearman's rank correlation rho
#>
#> data: velocity and steps
#> S = 160, p-value = 0.002008
#> alternative hypothesis: true rho is not equal to 0
#> sample estimates:
#> rho
#> -0.9047619
#>
#>
#> $Track_01$trend
#> [1] "Deceleration"
#>
#>
#> $Track_02
#> $Track_02$correlation
#>
#> Spearman's rank correlation rho
#>
#> data: velocity and steps
#> S = 42, p-value = 0.207
#> alternative hypothesis: true rho is not equal to 0
#> sample estimates:
#> rho
#> 0.5
#>
#>
#> $Track_02$trend
#> [1] "Steady"
#>
#>
#> $Track_03
#> $Track_03$correlation
#>
#> Spearman's rank correlation rho
#>
#> data: velocity and steps
#> S = 12, p-value = 0.8
#> alternative hypothesis: true rho is not equal to 0
#> sample estimates:
#> rho
#> -0.2
#>
#>
#> $Track_03$trend
#> [1] "Steady"
#>
#>
#> $Track_04
#> $Track_04$correlation
#>
#> Spearman's rank correlation rho
#>
#> data: velocity and steps
#> S = 18, p-value = 0.2
#> alternative hypothesis: true rho is not equal to 0
#> sample estimates:
#> rho
#> -0.8
#>
#>
#> $Track_04$trend
#> [1] "Steady"
#>
#>
#> $Track_05
#> [1] "Less than three steps"
#>
#> $Track_06
#> [1] "Less than three steps"
#>
#> $Track_07
#> $Track_07$correlation
#>
#> Spearman's rank correlation rho
#>
#> data: velocity and steps
#> S = 12, p-value = 0.1562
#> alternative hypothesis: true rho is not equal to 0
#> sample estimates:
#> rho
#> 0.6571429
#>
#>
#> $Track_07$trend
#> [1] "Steady"
#>
#>
#> $Track_08
#> $Track_08$correlation
#>
#> Spearman's rank correlation rho
#>
#> data: velocity and steps
#> S = 20, p-value = 1
#> alternative hypothesis: true rho is not equal to 0
#> sample estimates:
#> rho
#> 0
#>
#>
#> $Track_08$trend
#> [1] "Steady"
#>
#>
#> $Track_09
#> $Track_09$correlation
#>
#> Spearman's rank correlation rho
#>
#> data: velocity and steps
#> S = 20, p-value < 2.2e-16
#> alternative hypothesis: true rho is not equal to 0
#> sample estimates:
#> rho
#> -1
#>
#>
#> $Track_09$trend
#> [1] "Deceleration"
#>
#>
#> $Track_10
#> [1] "Less than three steps"
#>
#> $Track_11
#> [1] "Less than three steps"
#>
#> $Track_12
#> [1] "Less than three steps"
#>
#> $Track_13
#> $Track_13$correlation
#>
#> Spearman's rank correlation rho
#>
#> data: velocity and steps
#> S = 14, p-value = 0.6
#> alternative hypothesis: true rho is not equal to 0
#> sample estimates:
#> rho
#> -0.4
#>
#>
#> $Track_13$trend
#> [1] "Steady"
#>
#>
#> $Track_14
#> [1] "Less than three steps"
#>
#> $Track_15
#> $Track_15$correlation
#>
#> Spearman's rank correlation rho
#>
#> data: velocity and steps
#> S = 6, p-value = 0.6
#> alternative hypothesis: true rho is not equal to 0
#> sample estimates:
#> rho
#> 0.4
#>
#>
#> $Track_15$trend
#> [1] "Steady"
#>
#>
#> $Track_16
#> $Track_16$correlation
#>
#> Spearman's rank correlation rho
#>
#> data: velocity and steps
#> S = 30, p-value = 0.2939
#> alternative hypothesis: true rho is not equal to 0
#> sample estimates:
#> rho
#> 0.4642857
#>
#>
#> $Track_16$trend
#> [1] "Steady"
#>
#>
#> $Track_17
#> [1] "Less than three steps"
#>
#> $Track_18
#> $Track_18$correlation
#>
#> Spearman's rank correlation rho
#>
#> data: velocity and steps
#> S = 14, p-value = 0.6
#> alternative hypothesis: true rho is not equal to 0
#> sample estimates:
#> rho
#> -0.4
#>
#>
#> $Track_18$trend
#> [1] "Steady"
#>
#>
#> $Track_19
#> [1] "Less than three steps"
#>
#> $Track_20
#> [1] "Less than three steps"
#>
#> $Track_21
#> [1] "Less than three steps"
#>
#> $Track_22
#> [1] "Less than three steps"
#>
#> $Track_23
#> [1] "Less than three steps"Testing for Differences in Direction
The test_direction() function provides
a powerful statistical framework for comparing
directions across different tracks within a
track R object. It offers three distinct
methods for this purpose, which can be selected using the
analysis argument: ANOVA,
Kruskal-Wallis test, and Generalized Linear
Models (GLM), ensuring robust analysis even when assumptions
about data distribution and variance homogeneity are violated. The
function requires that each track contains more than three
footprints to be included in the analysis, as statistical tests
for comparing mean directions require a sufficient sample size to
generate meaningful results. This threshold ensures that the comparisons
are statistically reliable and robust.
When using the "ANOVA" option, the
function first checks the normality of the data through
the Shapiro-Wilk test and assesses homogeneity
of variances using Levene’s test. If these
assumptions are violated, the user is advised to consider the
Kruskal-Wallis or GLM methods instead.
The ANOVA method compares mean directions
across tracks, and if significant differences are detected,
Tukey’s HSD test is applied to perform post-hoc
pairwise comparisons. The
"Kruskal-Wallis" option, in contrast,
offers a non-parametric approach that compares median
directions across tracks and applies Dunn’s
test for pairwise comparisons if significant differences are
found. This method is particularly suitable when data do not meet the
assumptions required for parametric tests. Alternatively, if the
"GLM" option is selected, the function
applies a Generalized Linear Model (GLM) with a
Gaussian family to compare mean
directions. The emmeans package
is then used to compute pairwise comparisons, with
adjustments for multiple comparisons following Tukey’s
method, offering a flexible approach when dealing with complex
data distributions or deviations from normality.
The test_direction() function returns
list with a detailed set of results. It provides a normality
results matrix containing the Shapiro-Wilk test
statistic and p-value for each track, allowing the
user to evaluate whether the data follows a normal distribution. The
function also outputs the result of Levene’s test,
including the p-value used to assess whether variances
across tracks are homogeneous. When the ANOVA method is
selected, the function delivers the ANOVA table along
with Tukey HSD post-hoc results, enabling a thorough
examination of differences between groups. For the
Kruskal-Wallis test, the function returns the overall
test result alongside Dunn’s test post-hoc comparisons,
providing a non-parametric alternative for analyzing differences in
central tendency. In the case of GLM, the output
includes a summary of the model fit along with the pairwise
comparisons calculated via the emmeans
package, providing an efficient method to detect significant
differences while accommodating more complex statistical models.
The flexibility and comprehensiveness of the
test_direction() function make it a
versatile tool for comparing directional data across
multiple tracks. Its ability to perform parametric,
non-parametric, and generalized linear model analyses ensures
that researchers can robustly test hypotheses related to
movement patterns, group behavior, and ecological
interactions, regardless of the underlying data structure.
Examples of Usage
Testing with ANOVA checks for differences in mean directions across tracks, assuming the data is normally distributed and variances are homogeneous. Post-hoc pairwise comparisons are conducted if significant differences are found.
test_direction(PaluxyRiver, analysis = "Watson-Williams")#> $assumption_results
#> $assumption_results$rayleigh
#> statistic p_value
#> Trackway 1 0.9886376 5.798188e-12
#> Trackway 2 0.9892781 4.254234e-10
#>
#> $assumption_results$kappa
#> Trackway 1 Trackway 2
#> 0.3090983 0.1880619
#>
#> $assumption_results$kappa_range
#> [1] 0.1210364
#>
#> $assumption_results$kappa_ratio
#> [1] 1.643599
#>
#>
#> $global_test
#>
#> Watson-Williams test for homogeneity of means
#>
#> data: all_circ by groups
#> F = 0.017543, df1 = 1, df2 = 51, p-value = 0.8952
#> sample estimates:
#> Circular Data:
#> Type = angles
#> Units = radians
#> Template = none
#> Modulo = 2pi
#> Zero = 0
#> Rotation = counter
#> mean of Trackway 1 mean of Trackway 2
#> 3.161001 3.068109
#>
#>
#> $pairwise
#> track1 track2 statistic p_value method p_adj
#> 1 Trackway 1 Trackway 2 0.01754253 0.895151 Watson-Williams 0.895151
test_direction(MountTom, analysis = "Watson-Williams")#> $assumption_results
#> $assumption_results$rayleigh
#> statistic p_value
#> Trackway 01 0.9976355 0.000000000
#> Trackway 02 0.9966997 0.000000000
#> Trackway 03 0.9997300 0.001043937
#> Trackway 04 0.9966016 0.001161187
#> Trackway 07 0.9905355 0.000000000
#> Trackway 08 0.9987424 0.000000000
#> Trackway 09 0.9987039 0.001081750
#> Trackway 13 0.9861080 0.001598982
#> Trackway 15 0.9978616 0.001113260
#> Trackway 16 0.9928830 0.000000000
#> Trackway 18 0.9994406 0.001054538
#>
#> $assumption_results$kappa
#> Trackway 01 Trackway 02 Trackway 03 Trackway 04 Trackway 07 Trackway 08
#> 0.3910399 0.5495348 0.7396528 2.0773420 0.4103972 0.3654361
#> Trackway 09 Trackway 13 Trackway 15 Trackway 16 Trackway 18
#> 1.5453896 4.2678523 0.9589439 1.5269202 0.3557234
#>
#> $assumption_results$kappa_range
#> [1] 3.912129
#>
#> $assumption_results$kappa_ratio
#> [1] 11.99767
#>
#>
#> $global_test
#>
#> Watson-Williams test for homogeneity of means
#>
#> data: all_circ by groups
#> F = 8.3882, df1 = 10, df2 = 58, p-value = 2.974e-08
#> sample estimates:
#> Circular Data:
#> Type = angles
#> Units = radians
#> Template = none
#> Modulo = 2pi
#> Zero = 0
#> Rotation = counter
#> mean of Trackway 01 mean of Trackway 02 mean of Trackway 03 mean of Trackway 04
#> 3.1366963 1.5386635 0.7346896 0.8368350
#> mean of Trackway 07 mean of Trackway 08 mean of Trackway 09 mean of Trackway 13
#> 0.6327396 3.9810186 0.6642104 5.5461275
#> mean of Trackway 15 mean of Trackway 16 mean of Trackway 18
#> 0.7123928 3.3851511 3.4537059
#>
#>
#> $pairwise
#> track1 track2 statistic p_value method p_adj
#> 1 Trackway 01 Trackway 02 2.980766e+00 0.1035129494 Watson-Williams 1.00000000
#> 2 Trackway 01 Trackway 03 7.776502e+00 0.0163858701 Watson-Williams 0.70459241
#> 3 Trackway 01 Trackway 04 6.833837e+00 0.0226273246 Watson-Williams 0.88246566
#> 4 Trackway 01 Trackway 07 8.962760e+00 0.0096698571 Watson-Williams 0.47382300
#> 5 Trackway 01 Trackway 08 5.148557e-01 0.4857388086 Watson-Williams 1.00000000
#> 6 Trackway 01 Trackway 09 8.280785e+00 0.0138914601 Watson-Williams 0.62404466
#> 7 Trackway 01 Trackway 13 7.550041e+00 0.0176763298 Watson-Williams 0.74240585
#> 8 Trackway 01 Trackway 15 8.286101e+00 0.0138676592 Watson-Williams 0.62404466
#> 9 Trackway 01 Trackway 16 8.173556e-02 0.7788694550 Watson-Williams 1.00000000
#> 10 Trackway 01 Trackway 18 6.138353e-02 0.8085110205 Watson-Williams 1.00000000
#> 11 Trackway 02 Trackway 03 6.466307e-01 0.4369608130 Watson-Williams 1.00000000
#> 12 Trackway 02 Trackway 04 7.400587e-01 0.4065015185 Watson-Williams 1.00000000
#> 13 Trackway 02 Trackway 07 7.555391e-01 0.3993852496 Watson-Williams 1.00000000
#> 14 Trackway 02 Trackway 08 5.219097e+00 0.0397834262 Watson-Williams 1.00000000
#> 15 Trackway 02 Trackway 09 1.054881e+00 0.3246442132 Watson-Williams 1.00000000
#> 16 Trackway 02 Trackway 13 9.891294e+00 0.0084523834 Watson-Williams 0.42261917
#> 17 Trackway 02 Trackway 15 7.759792e-01 0.3956743468 Watson-Williams 1.00000000
#> 18 Trackway 02 Trackway 16 6.154840e+00 0.0254466930 Watson-Williams 0.96697433
#> 19 Trackway 02 Trackway 18 2.440906e+00 0.1441822582 Watson-Williams 1.00000000
#> 20 Trackway 03 Trackway 04 1.345343e-02 0.9105200633 Watson-Williams 1.00000000
#> 21 Trackway 03 Trackway 07 7.709723e-03 0.9317650933 Watson-Williams 1.00000000
#> 22 Trackway 03 Trackway 08 9.572190e+00 0.0128484173 Watson-Williams 0.59102720
#> 23 Trackway 03 Trackway 09 5.656749e-03 0.9418933046 Watson-Williams 1.00000000
#> 24 Trackway 03 Trackway 13 3.423479e+00 0.1014354369 Watson-Williams 1.00000000
#> 25 Trackway 03 Trackway 15 4.526982e-04 0.9835460333 Watson-Williams 1.00000000
#> 26 Trackway 03 Trackway 16 9.150469e+00 0.0115525818 Watson-Williams 0.54297135
#> 27 Trackway 03 Trackway 18 4.979097e+00 0.0561751241 Watson-Williams 1.00000000
#> 28 Trackway 04 Trackway 07 4.216512e-02 0.8414250349 Watson-Williams 1.00000000
#> 29 Trackway 04 Trackway 08 5.522642e+00 0.0433029414 Watson-Williams 1.00000000
#> 30 Trackway 04 Trackway 09 6.963350e-02 0.7985413218 Watson-Williams 1.00000000
#> 31 Trackway 04 Trackway 13 1.130779e+01 0.0098919936 Watson-Williams 0.47481569
#> 32 Trackway 04 Trackway 15 2.468287e-02 0.8790525990 Watson-Williams 1.00000000
#> 33 Trackway 04 Trackway 16 2.520577e+01 0.0003897153 Watson-Williams 0.02143434
#> 34 Trackway 04 Trackway 18 3.755804e+00 0.0886209669 Watson-Williams 1.00000000
#> 35 Trackway 07 Trackway 08 1.486631e+01 0.0026731350 Watson-Williams 0.13900302
#> 36 Trackway 07 Trackway 09 9.275838e-04 0.9763024577 Watson-Williams 1.00000000
#> 37 Trackway 07 Trackway 13 2.119573e+00 0.1760930088 Watson-Williams 1.00000000
#> 38 Trackway 07 Trackway 15 5.139236e-03 0.9442633451 Watson-Williams 1.00000000
#> 39 Trackway 07 Trackway 16 6.989221e+00 0.0202524744 Watson-Williams 0.81918239
#> 40 Trackway 07 Trackway 18 7.641635e+00 0.0199800583 Watson-Williams 0.81918239
#> 41 Trackway 08 Trackway 09 5.630774e+00 0.0417085367 Watson-Williams 1.00000000
#> 42 Trackway 08 Trackway 13 2.163339e+00 0.1754143713 Watson-Williams 1.00000000
#> 43 Trackway 08 Trackway 15 7.103917e+00 0.0258198163 Watson-Williams 0.96697433
#> 44 Trackway 08 Trackway 16 3.234319e-01 0.5800404171 Watson-Williams 1.00000000
#> 45 Trackway 08 Trackway 18 1.379765e-01 0.7188949441 Watson-Williams 1.00000000
#> 46 Trackway 09 Trackway 13 6.592936e+00 0.0332477844 Watson-Williams 1.00000000
#> 47 Trackway 09 Trackway 15 3.206817e-03 0.9562297400 Watson-Williams 1.00000000
#> 48 Trackway 09 Trackway 16 2.348867e+01 0.0005136178 Watson-Williams 0.02773536
#> 49 Trackway 09 Trackway 18 4.003953e+00 0.0803930903 Watson-Williams 1.00000000
#> 50 Trackway 13 Trackway 15 4.338768e+00 0.0707874930 Watson-Williams 1.00000000
#> 51 Trackway 13 Trackway 16 2.147301e+01 0.0007237989 Watson-Williams 0.03836134
#> 52 Trackway 13 Trackway 18 2.979469e+00 0.1226030066 Watson-Williams 1.00000000
#> 53 Trackway 15 Trackway 16 1.277916e+01 0.0043582591 Watson-Williams 0.22227121
#> 54 Trackway 15 Trackway 18 4.384561e+00 0.0695909887 Watson-Williams 1.00000000
#> 55 Trackway 16 Trackway 18 3.637189e-03 0.9529912151 Watson-Williams 1.00000000Testing with Kruskal-Wallis provides a non-parametric alternative for comparing median directions across tracks when the data does not meet the assumptions of ANOVA. Significant differences are further examined using Dunn’s test.
test_direction(PaluxyRiver, analysis = "Watson-Wheeler")#> $assumption_results
#> $assumption_results$rayleigh
#> statistic p_value
#> Trackway 1 0.9886376 5.798188e-12
#> Trackway 2 0.9892781 4.254234e-10
#>
#> $assumption_results$kappa
#> Trackway 1 Trackway 2
#> 0.3090983 0.1880619
#>
#> $assumption_results$kappa_range
#> [1] 0.1210364
#>
#> $assumption_results$kappa_ratio
#> [1] 1.643599
#>
#>
#> $global_test
#>
#> Watson-Wheeler (permutation, B=1000)
#>
#> data:
#> W = 0.0010818, p-value = 1
#>
#>
#> $pairwise
#> track1 track2 statistic p_value
#> 1 Trackway 1 Trackway 2 0.001081754 1
#> method p_adj
#> 1 Watson-Wheeler (permutation, B=1000) 1
test_direction(MountTom, analysis = "Watson-Wheeler")#> $assumption_results
#> $assumption_results$rayleigh
#> statistic p_value
#> Trackway 01 0.9976355 0.000000000
#> Trackway 02 0.9966997 0.000000000
#> Trackway 03 0.9997300 0.001043937
#> Trackway 04 0.9966016 0.001161187
#> Trackway 07 0.9905355 0.000000000
#> Trackway 08 0.9987424 0.000000000
#> Trackway 09 0.9987039 0.001081750
#> Trackway 13 0.9861080 0.001598982
#> Trackway 15 0.9978616 0.001113260
#> Trackway 16 0.9928830 0.000000000
#> Trackway 18 0.9994406 0.001054538
#>
#> $assumption_results$kappa
#> Trackway 01 Trackway 02 Trackway 03 Trackway 04 Trackway 07 Trackway 08
#> 0.3910399 0.5495348 0.7396528 2.0773420 0.4103972 0.3654361
#> Trackway 09 Trackway 13 Trackway 15 Trackway 16 Trackway 18
#> 1.5453896 4.2678523 0.9589439 1.5269202 0.3557234
#>
#> $assumption_results$kappa_range
#> [1] 3.912129
#>
#> $assumption_results$kappa_ratio
#> [1] 11.99767
#>
#>
#> $global_test
#>
#> Watson-Wheeler (permutation, B=1000)
#>
#> data:
#> W = 25.149, p-value = 0.2088
#>
#>
#> $pairwise
#> track1 track2 statistic p_value
#> 1 Trackway 01 Trackway 02 1.9529867 0.381618382
#> 2 Trackway 01 Trackway 03 1.2543066 0.545454545
#> 3 Trackway 01 Trackway 04 5.1647562 0.057942058
#> 4 Trackway 01 Trackway 07 0.8576608 0.653346653
#> 5 Trackway 01 Trackway 08 0.3961129 0.810189810
#> 6 Trackway 01 Trackway 09 3.9935156 0.138861139
#> 7 Trackway 01 Trackway 13 1.7968405 0.376623377
#> 8 Trackway 01 Trackway 15 2.9171522 0.213786214
#> 9 Trackway 01 Trackway 16 1.6129754 0.490509491
#> 10 Trackway 01 Trackway 18 0.5777778 0.740259740
#> 11 Trackway 02 Trackway 03 2.7744529 0.295704296
#> 12 Trackway 02 Trackway 04 3.7520653 0.179820180
#> 13 Trackway 02 Trackway 07 0.8576608 0.667332667
#> 14 Trackway 02 Trackway 08 0.8062315 0.696303696
#> 15 Trackway 02 Trackway 09 1.9904686 0.369630370
#> 16 Trackway 02 Trackway 13 3.7520653 0.147852148
#> 17 Trackway 02 Trackway 15 1.1555556 0.577422577
#> 18 Trackway 02 Trackway 16 3.6113309 0.139860140
#> 19 Trackway 02 Trackway 18 1.0128562 0.604395604
#> 20 Trackway 03 Trackway 04 3.3249845 0.258741259
#> 21 Trackway 03 Trackway 07 0.6285714 0.814185814
#> 22 Trackway 03 Trackway 08 1.4782138 0.517482517
#> 23 Trackway 03 Trackway 09 0.1050466 0.987012987
#> 24 Trackway 03 Trackway 13 3.3249845 0.175824176
#> 25 Trackway 03 Trackway 15 0.7200000 0.859140859
#> 26 Trackway 03 Trackway 16 6.0910205 0.039960040
#> 27 Trackway 03 Trackway 18 0.7200000 0.796203796
#> 28 Trackway 04 Trackway 07 0.6285714 0.693306693
#> 29 Trackway 04 Trackway 08 2.6833945 0.307692308
#> 30 Trackway 04 Trackway 09 3.3249845 0.178821179
#> 31 Trackway 04 Trackway 13 4.9349534 0.118881119
#> 32 Trackway 04 Trackway 15 0.2750155 0.875124875
#> 33 Trackway 04 Trackway 16 6.0910205 0.031968032
#> 34 Trackway 04 Trackway 18 0.7200000 0.670329670
#> 35 Trackway 07 Trackway 08 0.5458271 0.769230769
#> 36 Trackway 07 Trackway 09 0.1684252 0.904095904
#> 37 Trackway 07 Trackway 13 8.7548706 0.005994006
#> 38 Trackway 07 Trackway 15 0.6285714 0.842157842
#> 39 Trackway 07 Trackway 16 4.5961816 0.093906094
#> 40 Trackway 07 Trackway 18 1.2571429 0.608391608
#> 41 Trackway 08 Trackway 09 1.4782138 0.516483516
#> 42 Trackway 08 Trackway 13 8.2290250 0.006993007
#> 43 Trackway 08 Trackway 15 2.0000000 0.372627373
#> 44 Trackway 08 Trackway 16 5.4696605 0.052947053
#> 45 Trackway 08 Trackway 18 0.1667894 0.981018981
#> 46 Trackway 09 Trackway 13 3.3249845 0.290709291
#> 47 Trackway 09 Trackway 15 0.7200000 0.717282717
#> 48 Trackway 09 Trackway 16 6.0910205 0.047952048
#> 49 Trackway 09 Trackway 18 0.7200000 0.814185814
#> 50 Trackway 13 Trackway 15 4.9349534 0.131868132
#> 51 Trackway 13 Trackway 16 9.1589842 0.012987013
#> 52 Trackway 13 Trackway 18 7.5399379 0.023976024
#> 53 Trackway 15 Trackway 16 6.0910205 0.035964036
#> 54 Trackway 15 Trackway 18 0.7200000 0.813186813
#> 55 Trackway 16 Trackway 18 3.1237388 0.236763237
#> method p_adj
#> 1 Watson-Wheeler (permutation, B=1000) 1.0000000
#> 2 Watson-Wheeler (permutation, B=1000) 1.0000000
#> 3 Watson-Wheeler (permutation, B=1000) 1.0000000
#> 4 Watson-Wheeler (permutation, B=1000) 1.0000000
#> 5 Watson-Wheeler (permutation, B=1000) 1.0000000
#> 6 Watson-Wheeler (permutation, B=1000) 1.0000000
#> 7 Watson-Wheeler (permutation, B=1000) 1.0000000
#> 8 Watson-Wheeler (permutation, B=1000) 1.0000000
#> 9 Watson-Wheeler (permutation, B=1000) 1.0000000
#> 10 Watson-Wheeler (permutation, B=1000) 1.0000000
#> 11 Watson-Wheeler (permutation, B=1000) 1.0000000
#> 12 Watson-Wheeler (permutation, B=1000) 1.0000000
#> 13 Watson-Wheeler (permutation, B=1000) 1.0000000
#> 14 Watson-Wheeler (permutation, B=1000) 1.0000000
#> 15 Watson-Wheeler (permutation, B=1000) 1.0000000
#> 16 Watson-Wheeler (permutation, B=1000) 1.0000000
#> 17 Watson-Wheeler (permutation, B=1000) 1.0000000
#> 18 Watson-Wheeler (permutation, B=1000) 1.0000000
#> 19 Watson-Wheeler (permutation, B=1000) 1.0000000
#> 20 Watson-Wheeler (permutation, B=1000) 1.0000000
#> 21 Watson-Wheeler (permutation, B=1000) 1.0000000
#> 22 Watson-Wheeler (permutation, B=1000) 1.0000000
#> 23 Watson-Wheeler (permutation, B=1000) 1.0000000
#> 24 Watson-Wheeler (permutation, B=1000) 1.0000000
#> 25 Watson-Wheeler (permutation, B=1000) 1.0000000
#> 26 Watson-Wheeler (permutation, B=1000) 1.0000000
#> 27 Watson-Wheeler (permutation, B=1000) 1.0000000
#> 28 Watson-Wheeler (permutation, B=1000) 1.0000000
#> 29 Watson-Wheeler (permutation, B=1000) 1.0000000
#> 30 Watson-Wheeler (permutation, B=1000) 1.0000000
#> 31 Watson-Wheeler (permutation, B=1000) 1.0000000
#> 32 Watson-Wheeler (permutation, B=1000) 1.0000000
#> 33 Watson-Wheeler (permutation, B=1000) 1.0000000
#> 34 Watson-Wheeler (permutation, B=1000) 1.0000000
#> 35 Watson-Wheeler (permutation, B=1000) 1.0000000
#> 36 Watson-Wheeler (permutation, B=1000) 1.0000000
#> 37 Watson-Wheeler (permutation, B=1000) 0.3296703
#> 38 Watson-Wheeler (permutation, B=1000) 1.0000000
#> 39 Watson-Wheeler (permutation, B=1000) 1.0000000
#> 40 Watson-Wheeler (permutation, B=1000) 1.0000000
#> 41 Watson-Wheeler (permutation, B=1000) 1.0000000
#> 42 Watson-Wheeler (permutation, B=1000) 0.3776224
#> 43 Watson-Wheeler (permutation, B=1000) 1.0000000
#> 44 Watson-Wheeler (permutation, B=1000) 1.0000000
#> 45 Watson-Wheeler (permutation, B=1000) 1.0000000
#> 46 Watson-Wheeler (permutation, B=1000) 1.0000000
#> 47 Watson-Wheeler (permutation, B=1000) 1.0000000
#> 48 Watson-Wheeler (permutation, B=1000) 1.0000000
#> 49 Watson-Wheeler (permutation, B=1000) 1.0000000
#> 50 Watson-Wheeler (permutation, B=1000) 1.0000000
#> 51 Watson-Wheeler (permutation, B=1000) 0.6883117
#> 52 Watson-Wheeler (permutation, B=1000) 1.0000000
#> 53 Watson-Wheeler (permutation, B=1000) 1.0000000
#> 54 Watson-Wheeler (permutation, B=1000) 1.0000000
#> 55 Watson-Wheeler (permutation, B=1000) 1.0000000Simulating Tracks Using Different Movement Models
The simulate_track() function generates
simulated movement trajectories based on an existing
set of tracks. It offers three distinct movement
models—Directed, Constrained, and
Unconstrained—each representing varying levels of
constraint in movement patterns. This flexibility allows users to model
scenarios reflecting biological or environmental
constraints, such as directed movement towards resources,
movement along geographical features, or free exploratory behavior.
The Directed model is the most
constrained, simulating trajectories that follow a specific direction
based on the original track’s angular orientation. It
aims to maintain a consistent overall direction with minor deviations to
reflect natural variability. This model is useful for scenarios where
movement is highly directional, such as an animal
navigating toward a known resource.
The Constrained model represents a
correlated random walk, where movement is not strictly
directional but is influenced by certain angular and linear
properties of the original track. This model allows for random
exploration while retaining some of the characteristics of the original
movement pattern. It is suitable for situations where animals navigate
with limited knowledge of their surroundings, such as
navigating within a bounded area without a specific
destination.
The Unconstrained model provides the
most flexibility, simulating trajectories that represent
exploratory or dispersal behavior without directional
bias. It is based on a fully random walk with
the starting direction randomly determined for each simulation. This
model is appropriate for scenarios where animals are moving through
unfamiliar or homogeneous environments.
The simulate_track() function requires
several arguments to define the simulation process. The
data argument specifies the input as a
track R object. The nsim
argument defines the number of simulations to run, with a default value
of 1000 if not specified. This number represents a
recommended minimum to ensure stable and reliable
estimation of p-values, particularly when assessing the
statistical significance of observed trajectory features. Using fewer
simulations may result in imprecise or biased p-value estimates
due to insufficient sampling of the null distribution. The
model argument determines the type of
movement model to be used, which can be “Directed”,
“Constrained”, or “Unconstrained”,
with the default being “Unconstrained” if not
provided.
The function ensures that simulations are only applied to
trajectories with at least four steps, as calculating
the standard deviations of angles and step
lengths—essential for the simulation process—is not feasible
for shorter trajectories. In cases where tracks are too short, the user
is advised to use the subset_track()
function to exclude those tracks from the simulation process.
The simulate_track() function returns a
track simulation R object, which is a list
of simulated trajectories. Each simulation is stored separately,
providing users with the flexibility to visualize, analyze, and
compare these simulations against the original tracks to
evaluate movement constraints or explore
alternative movement hypotheses. This approach is
particularly useful for testing paleoecological and
paleoethological hypotheses, such as assessing whether observed
movement patterns are consistent with group behavior, resource-driven
navigation, or independent exploratory movement.
Examples of Usage
Simulating tracks from the Paluxy River and
Mount Tom datasets using the
Unconstrained, Directed, and
Constrained models. For the Mount Tom
dataset, tracks were preprocessed using
subset_track() to retain only those
containing at least four steps. Although the simulations were performed
with 100 simulated tracks, the examples below display
only a subset of 10 simulated tracks to prevent the
vignette from becoming excessively large. This approach ensures the
vignette remains efficient, clear, and easy to navigate.
sim_unconstrained_paluxy <- simulate_track(PaluxyRiver, nsim = 100, model = "Unconstrained")
print(sim_unconstrained_paluxy[1:10])#> [[1]]
#> [[1]][[1]]
#> x y time displacementTime polar
#> 1 0.696000 0.9460000 0.00 0.00 0.696000+0.9460000i
#> 2 1.028738 0.5602082 0.02 0.02 1.028738+0.5602082i
#> 3 1.350037 0.1555926 0.04 0.04 1.350037+0.1555926i
#> 4 1.673395 -0.2416320 0.06 0.06 1.673395-0.2416320i
#> 5 1.946584 -0.6079657 0.08 0.08 1.946584-0.6079657i
#> 6 2.310744 -1.0965548 0.10 0.10 2.310744-1.0965548i
#> 7 2.596401 -1.4164253 0.12 0.12 2.596401-1.4164253i
#> 8 2.899040 -1.7450152 0.14 0.14 2.899040-1.7450152i
#> 9 3.204250 -2.0890924 0.16 0.16 3.204250-2.0890924i
#> 10 3.534158 -2.4967033 0.18 0.18 3.534158-2.4967033i
#> 11 3.868453 -2.8400857 0.20 0.20 3.868453-2.8400857i
#> 12 4.287867 -3.2126432 0.22 0.22 4.287867-3.2126432i
#> 13 4.657263 -3.5717230 0.24 0.24 4.657263-3.5717230i
#> 14 5.055952 -3.9299620 0.26 0.26 5.055952-3.9299620i
#> 15 5.443434 -4.2552891 0.28 0.28 5.443434-4.2552891i
#> 16 5.923291 -4.6357454 0.30 0.30 5.923291-4.6357454i
#> 17 6.268389 -4.9403297 0.32 0.32 6.268389-4.9403297i
#> 18 6.598541 -5.2905543 0.34 0.34 6.598541-5.2905543i
#> 19 7.024494 -5.6801095 0.36 0.36 7.024494-5.6801095i
#> 20 7.381154 -6.0228278 0.38 0.38 7.381154-6.0228278i
#> 21 7.731644 -6.3439618 0.40 0.40 7.731644-6.3439618i
#> 22 8.083808 -6.6663897 0.42 0.42 8.083808-6.6663897i
#> 23 8.464424 -6.9774324 0.44 0.44 8.464424-6.9774324i
#> 24 8.877143 -7.3423549 0.46 0.46 8.877143-7.3423549i
#> 25 9.269954 -7.7760519 0.48 0.48 9.269954-7.7760519i
#> 26 9.575341 -8.1061964 0.50 0.50 9.575341-8.1061964i
#> 27 9.939018 -8.4847137 0.52 0.52 9.939018-8.4847137i
#> 28 10.308191 -8.8502346 0.54 0.54 10.308191-8.8502346i
#> 29 10.661451 -9.2254182 0.56 0.56 10.661451-9.2254182i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_1 Sim_1 TrajSim_1_1
#> 2 0.3327377-0.3857918i Traj_1 Sim_1 TrajSim_1_1
#> 3 0.3212993-0.4046156i Traj_1 Sim_1 TrajSim_1_1
#> 4 0.3233578-0.3972246i Traj_1 Sim_1 TrajSim_1_1
#> 5 0.2731887-0.3663337i Traj_1 Sim_1 TrajSim_1_1
#> 6 0.3641606-0.4885891i Traj_1 Sim_1 TrajSim_1_1
#> 7 0.2856567-0.3198705i Traj_1 Sim_1 TrajSim_1_1
#> 8 0.3026388-0.3285899i Traj_1 Sim_1 TrajSim_1_1
#> 9 0.3052101-0.3440772i Traj_1 Sim_1 TrajSim_1_1
#> 10 0.3299079-0.4076109i Traj_1 Sim_1 TrajSim_1_1
#> 11 0.3342952-0.3433825i Traj_1 Sim_1 TrajSim_1_1
#> 12 0.4194138-0.3725575i Traj_1 Sim_1 TrajSim_1_1
#> 13 0.3693964-0.3590798i Traj_1 Sim_1 TrajSim_1_1
#> 14 0.3986894-0.3582390i Traj_1 Sim_1 TrajSim_1_1
#> 15 0.3874814-0.3253271i Traj_1 Sim_1 TrajSim_1_1
#> 16 0.4798569-0.3804563i Traj_1 Sim_1 TrajSim_1_1
#> 17 0.3450980-0.3045843i Traj_1 Sim_1 TrajSim_1_1
#> 18 0.3301521-0.3502246i Traj_1 Sim_1 TrajSim_1_1
#> 19 0.4259527-0.3895552i Traj_1 Sim_1 TrajSim_1_1
#> 20 0.3566601-0.3427183i Traj_1 Sim_1 TrajSim_1_1
#> 21 0.3504908-0.3211340i Traj_1 Sim_1 TrajSim_1_1
#> 22 0.3521638-0.3224279i Traj_1 Sim_1 TrajSim_1_1
#> 23 0.3806155-0.3110427i Traj_1 Sim_1 TrajSim_1_1
#> 24 0.4127190-0.3649224i Traj_1 Sim_1 TrajSim_1_1
#> 25 0.3928109-0.4336970i Traj_1 Sim_1 TrajSim_1_1
#> 26 0.3053875-0.3301445i Traj_1 Sim_1 TrajSim_1_1
#> 27 0.3636767-0.3785173i Traj_1 Sim_1 TrajSim_1_1
#> 28 0.3691735-0.3655210i Traj_1 Sim_1 TrajSim_1_1
#> 29 0.3532601-0.3751836i Traj_1 Sim_1 TrajSim_1_1
#>
#> [[1]][[2]]
#> x y time displacementTime polar
#> 1 0.3360000 1.5600000 0.00 0.00 0.3360000+1.5600000i
#> 2 0.1048574 1.1671839 0.02 0.02 0.1048574+1.1671839i
#> 3 -0.1824684 0.6225599 0.04 0.04 -0.1824684+0.6225599i
#> 4 -0.4658288 0.1403592 0.06 0.06 -0.4658288+0.1403592i
#> 5 -0.8431547 -0.3648615 0.08 0.08 -0.8431547-0.3648615i
#> 6 -1.1541191 -0.9240261 0.10 0.10 -1.1541191-0.9240261i
#> 7 -1.3423068 -1.5005196 0.12 0.12 -1.3423068-1.5005196i
#> 8 -1.6260483 -2.0986801 0.14 0.14 -1.6260483-2.0986801i
#> 9 -1.8736053 -2.6546951 0.16 0.16 -1.8736053-2.6546951i
#> 10 -2.1932556 -3.2460287 0.18 0.18 -2.1932556-3.2460287i
#> 11 -2.3852338 -3.7682818 0.20 0.20 -2.3852338-3.7682818i
#> 12 -2.6497906 -4.3348951 0.22 0.22 -2.6497906-4.3348951i
#> 13 -2.9518620 -4.7798785 0.24 0.24 -2.9518620-4.7798785i
#> 14 -3.3894406 -5.3756776 0.26 0.26 -3.3894406-5.3756776i
#> 15 -3.8766340 -5.7673587 0.28 0.28 -3.8766340-5.7673587i
#> 16 -4.4284599 -6.1076819 0.30 0.30 -4.4284599-6.1076819i
#> 17 -4.9865540 -6.4431337 0.32 0.32 -4.9865540-6.4431337i
#> 18 -5.4500965 -6.8000745 0.34 0.34 -5.4500965-6.8000745i
#> 19 -5.9329102 -7.1649438 0.36 0.36 -5.9329102-7.1649438i
#> 20 -6.2934915 -7.4522740 0.38 0.38 -6.2934915-7.4522740i
#> 21 -6.8320702 -7.7333950 0.40 0.40 -6.8320702-7.7333950i
#> 22 -7.3768848 -8.0492434 0.42 0.42 -7.3768848-8.0492434i
#> 23 -8.0298452 -8.3824090 0.44 0.44 -8.0298452-8.3824090i
#> 24 -8.7408216 -8.6957133 0.46 0.46 -8.7408216-8.6957133i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_2 Sim_1 TrajSim_2_1
#> 2 -0.2311426-0.3928161i Traj_2 Sim_1 TrajSim_2_1
#> 3 -0.2873258-0.5446240i Traj_2 Sim_1 TrajSim_2_1
#> 4 -0.2833605-0.4822007i Traj_2 Sim_1 TrajSim_2_1
#> 5 -0.3773258-0.5052208i Traj_2 Sim_1 TrajSim_2_1
#> 6 -0.3109645-0.5591646i Traj_2 Sim_1 TrajSim_2_1
#> 7 -0.1881877-0.5764934i Traj_2 Sim_1 TrajSim_2_1
#> 8 -0.2837415-0.5981606i Traj_2 Sim_1 TrajSim_2_1
#> 9 -0.2475569-0.5560150i Traj_2 Sim_1 TrajSim_2_1
#> 10 -0.3196503-0.5913335i Traj_2 Sim_1 TrajSim_2_1
#> 11 -0.1919782-0.5222531i Traj_2 Sim_1 TrajSim_2_1
#> 12 -0.2645568-0.5666134i Traj_2 Sim_1 TrajSim_2_1
#> 13 -0.3020714-0.4449834i Traj_2 Sim_1 TrajSim_2_1
#> 14 -0.4375786-0.5957991i Traj_2 Sim_1 TrajSim_2_1
#> 15 -0.4871933-0.3916810i Traj_2 Sim_1 TrajSim_2_1
#> 16 -0.5518260-0.3403232i Traj_2 Sim_1 TrajSim_2_1
#> 17 -0.5580940-0.3354518i Traj_2 Sim_1 TrajSim_2_1
#> 18 -0.4635425-0.3569408i Traj_2 Sim_1 TrajSim_2_1
#> 19 -0.4828138-0.3648693i Traj_2 Sim_1 TrajSim_2_1
#> 20 -0.3605813-0.2873302i Traj_2 Sim_1 TrajSim_2_1
#> 21 -0.5385787-0.2811210i Traj_2 Sim_1 TrajSim_2_1
#> 22 -0.5448146-0.3158484i Traj_2 Sim_1 TrajSim_2_1
#> 23 -0.6529604-0.3331656i Traj_2 Sim_1 TrajSim_2_1
#> 24 -0.7109764-0.3133043i Traj_2 Sim_1 TrajSim_2_1
#>
#>
#> [[2]]
#> [[2]][[1]]
#> x y time displacementTime polar
#> 1 0.696000 0.94600000 0.00 0.00 0.696000+0.94600000i
#> 2 1.232337 0.80849670 0.02 0.02 1.232337+0.80849670i
#> 3 1.784078 0.73816028 0.04 0.04 1.784078+0.73816028i
#> 4 2.338174 0.66954179 0.06 0.06 2.338174+0.66954179i
#> 5 2.879370 0.62967717 0.08 0.08 2.879370+0.62967717i
#> 6 3.398224 0.57935851 0.10 0.10 3.398224+0.57935851i
#> 7 3.915628 0.50477076 0.12 0.12 3.915628+0.50477076i
#> 8 4.496334 0.39329726 0.14 0.14 4.496334+0.39329726i
#> 9 5.024637 0.29334547 0.16 0.16 5.024637+0.29334547i
#> 10 5.570686 0.18554400 0.18 0.18 5.570686+0.18554400i
#> 11 6.127452 0.06739202 0.20 0.20 6.127452+0.06739202i
#> 12 6.679503 -0.12578754 0.22 0.22 6.679503-0.12578754i
#> 13 7.201439 -0.33379942 0.24 0.24 7.201439-0.33379942i
#> 14 7.711949 -0.56044136 0.26 0.26 7.711949-0.56044136i
#> 15 8.247164 -0.78330528 0.28 0.28 8.247164-0.78330528i
#> 16 8.711183 -1.03370637 0.30 0.30 8.711183-1.03370637i
#> 17 9.126155 -1.20079692 0.32 0.32 9.126155-1.20079692i
#> 18 9.695154 -1.37113344 0.34 0.34 9.695154-1.37113344i
#> 19 10.172718 -1.49882603 0.36 0.36 10.172718-1.49882603i
#> 20 10.623830 -1.64218621 0.38 0.38 10.623830-1.64218621i
#> 21 11.128942 -1.82084590 0.40 0.40 11.128942-1.82084590i
#> 22 11.623815 -1.98208795 0.42 0.42 11.623815-1.98208795i
#> 23 12.200676 -2.19148851 0.44 0.44 12.200676-2.19148851i
#> 24 12.584153 -2.39093036 0.46 0.46 12.584153-2.39093036i
#> 25 13.050732 -2.60056801 0.48 0.48 13.050732-2.60056801i
#> 26 13.541499 -2.82852820 0.50 0.50 13.541499-2.82852820i
#> 27 13.915918 -2.98473782 0.52 0.52 13.915918-2.98473782i
#> 28 14.435408 -3.23622826 0.54 0.54 14.435408-3.23622826i
#> 29 15.013027 -3.49441243 0.56 0.56 15.013027-3.49441243i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.00000000i Traj_1 Sim_2 TrajSim_1_2
#> 2 0.5363366-0.13750330i Traj_1 Sim_2 TrajSim_1_2
#> 3 0.5517412-0.07033643i Traj_1 Sim_2 TrajSim_1_2
#> 4 0.5540966-0.06861849i Traj_1 Sim_2 TrajSim_1_2
#> 5 0.5411957-0.03986462i Traj_1 Sim_2 TrajSim_1_2
#> 6 0.5188542-0.05031866i Traj_1 Sim_2 TrajSim_1_2
#> 7 0.5174040-0.07458775i Traj_1 Sim_2 TrajSim_1_2
#> 8 0.5807057-0.11147351i Traj_1 Sim_2 TrajSim_1_2
#> 9 0.5283030-0.09995179i Traj_1 Sim_2 TrajSim_1_2
#> 10 0.5460487-0.10780147i Traj_1 Sim_2 TrajSim_1_2
#> 11 0.5567662-0.11815198i Traj_1 Sim_2 TrajSim_1_2
#> 12 0.5520515-0.19317956i Traj_1 Sim_2 TrajSim_1_2
#> 13 0.5219352-0.20801188i Traj_1 Sim_2 TrajSim_1_2
#> 14 0.5105103-0.22664194i Traj_1 Sim_2 TrajSim_1_2
#> 15 0.5352149-0.22286392i Traj_1 Sim_2 TrajSim_1_2
#> 16 0.4640194-0.25040109i Traj_1 Sim_2 TrajSim_1_2
#> 17 0.4149716-0.16709055i Traj_1 Sim_2 TrajSim_1_2
#> 18 0.5689990-0.17033652i Traj_1 Sim_2 TrajSim_1_2
#> 19 0.4775639-0.12769259i Traj_1 Sim_2 TrajSim_1_2
#> 20 0.4511125-0.14336018i Traj_1 Sim_2 TrajSim_1_2
#> 21 0.5051116-0.17865968i Traj_1 Sim_2 TrajSim_1_2
#> 22 0.4948729-0.16124205i Traj_1 Sim_2 TrajSim_1_2
#> 23 0.5768610-0.20940056i Traj_1 Sim_2 TrajSim_1_2
#> 24 0.3834778-0.19944185i Traj_1 Sim_2 TrajSim_1_2
#> 25 0.4665790-0.20963765i Traj_1 Sim_2 TrajSim_1_2
#> 26 0.4907670-0.22796019i Traj_1 Sim_2 TrajSim_1_2
#> 27 0.3744186-0.15620962i Traj_1 Sim_2 TrajSim_1_2
#> 28 0.5194904-0.25149043i Traj_1 Sim_2 TrajSim_1_2
#> 29 0.5776187-0.25818417i Traj_1 Sim_2 TrajSim_1_2
#>
#> [[2]][[2]]
#> x y time displacementTime polar
#> 1 0.3360000 1.5600000 0.00 0.00 0.3360000+1.5600000i
#> 2 0.2013529 0.8169491 0.02 0.02 0.2013529+0.8169491i
#> 3 0.1655985 0.3274655 0.04 0.04 0.1655985+0.3274655i
#> 4 0.1167626 -0.2507414 0.06 0.06 0.1167626-0.2507414i
#> 5 0.1580102 -0.8108889 0.08 0.08 0.1580102-0.8108889i
#> 6 0.3100086 -1.4667725 0.10 0.10 0.3100086-1.4667725i
#> 7 0.5748883 -2.0422153 0.12 0.12 0.5748883-2.0422153i
#> 8 0.7698383 -2.5994474 0.14 0.14 0.7698383-2.5994474i
#> 9 0.9588824 -2.9334650 0.16 0.16 0.9588824-2.9334650i
#> 10 1.3279639 -3.4982301 0.18 0.18 1.3279639-3.4982301i
#> 11 1.6366677 -3.9054979 0.20 0.20 1.6366677-3.9054979i
#> 12 1.9778960 -4.4380081 0.22 0.22 1.9778960-4.4380081i
#> 13 2.3829518 -4.9390702 0.24 0.24 2.3829518-4.9390702i
#> 14 2.8618237 -5.2808746 0.26 0.26 2.8618237-5.2808746i
#> 15 3.3183853 -5.6320149 0.28 0.28 3.3183853-5.6320149i
#> 16 3.8250722 -6.0077753 0.30 0.30 3.8250722-6.0077753i
#> 17 4.3443954 -6.2984060 0.32 0.32 4.3443954-6.2984060i
#> 18 4.8411145 -6.5619879 0.34 0.34 4.8411145-6.5619879i
#> 19 5.3136298 -6.8305858 0.36 0.36 5.3136298-6.8305858i
#> 20 5.8929746 -7.3216100 0.38 0.38 5.8929746-7.3216100i
#> 21 6.2685749 -7.5825019 0.40 0.40 6.2685749-7.5825019i
#> 22 6.7609784 -7.8829597 0.42 0.42 6.7609784-7.8829597i
#> 23 7.2206164 -8.2516126 0.44 0.44 7.2206164-8.2516126i
#> 24 7.7437904 -8.5709561 0.46 0.46 7.7437904-8.5709561i
#> displacement Trajectory Simulation TrajSim
#> 1 0.00000000+0.0000000i Traj_2 Sim_2 TrajSim_2_2
#> 2 -0.13464709-0.7430509i Traj_2 Sim_2 TrajSim_2_2
#> 3 -0.03575438-0.4894836i Traj_2 Sim_2 TrajSim_2_2
#> 4 -0.04883589-0.5782068i Traj_2 Sim_2 TrajSim_2_2
#> 5 0.04124760-0.5601476i Traj_2 Sim_2 TrajSim_2_2
#> 6 0.15199837-0.6558836i Traj_2 Sim_2 TrajSim_2_2
#> 7 0.26487973-0.5754428i Traj_2 Sim_2 TrajSim_2_2
#> 8 0.19494994-0.5572321i Traj_2 Sim_2 TrajSim_2_2
#> 9 0.18904416-0.3340176i Traj_2 Sim_2 TrajSim_2_2
#> 10 0.36908143-0.5647651i Traj_2 Sim_2 TrajSim_2_2
#> 11 0.30870383-0.4072678i Traj_2 Sim_2 TrajSim_2_2
#> 12 0.34122834-0.5325102i Traj_2 Sim_2 TrajSim_2_2
#> 13 0.40505580-0.5010621i Traj_2 Sim_2 TrajSim_2_2
#> 14 0.47887189-0.3418044i Traj_2 Sim_2 TrajSim_2_2
#> 15 0.45656155-0.3511403i Traj_2 Sim_2 TrajSim_2_2
#> 16 0.50668695-0.3757605i Traj_2 Sim_2 TrajSim_2_2
#> 17 0.51932315-0.2906307i Traj_2 Sim_2 TrajSim_2_2
#> 18 0.49671910-0.2635819i Traj_2 Sim_2 TrajSim_2_2
#> 19 0.47251537-0.2685979i Traj_2 Sim_2 TrajSim_2_2
#> 20 0.57934477-0.4910241i Traj_2 Sim_2 TrajSim_2_2
#> 21 0.37560030-0.2608920i Traj_2 Sim_2 TrajSim_2_2
#> 22 0.49240350-0.3004577i Traj_2 Sim_2 TrajSim_2_2
#> 23 0.45963796-0.3686529i Traj_2 Sim_2 TrajSim_2_2
#> 24 0.52317402-0.3193436i Traj_2 Sim_2 TrajSim_2_2
#>
#>
#> [[3]]
#> [[3]][[1]]
#> x y time displacementTime polar
#> 1 0.69600000 0.946000 0.00 0.00 0.69600000+ 0.946000i
#> 2 0.32684882 1.360664 0.02 0.02 0.32684882+ 1.360664i
#> 3 -0.03667951 1.790658 0.04 0.04 -0.03667951+ 1.790658i
#> 4 -0.40093329 2.229600 0.06 0.06 -0.40093329+ 2.229600i
#> 5 -0.79664499 2.663398 0.08 0.08 -0.79664499+ 2.663398i
#> 6 -1.21460395 3.169701 0.10 0.10 -1.21460395+ 3.169701i
#> 7 -1.56148046 3.565229 0.12 0.12 -1.56148046+ 3.565229i
#> 8 -1.96987311 4.048515 0.14 0.14 -1.96987311+ 4.048515i
#> 9 -2.31327961 4.507860 0.16 0.16 -2.31327961+ 4.507860i
#> 10 -2.60009302 4.860925 0.18 0.18 -2.60009302+ 4.860925i
#> 11 -2.86494781 5.148025 0.20 0.20 -2.86494781+ 5.148025i
#> 12 -3.25715689 5.595814 0.22 0.22 -3.25715689+ 5.595814i
#> 13 -3.63664922 6.063379 0.24 0.24 -3.63664922+ 6.063379i
#> 14 -4.04793141 6.520388 0.26 0.26 -4.04793141+ 6.520388i
#> 15 -4.35996782 6.926706 0.28 0.28 -4.35996782+ 6.926706i
#> 16 -4.67946760 7.333183 0.30 0.30 -4.67946760+ 7.333183i
#> 17 -5.00203051 7.701967 0.32 0.32 -5.00203051+ 7.701967i
#> 18 -5.25575104 8.048493 0.34 0.34 -5.25575104+ 8.048493i
#> 19 -5.60388469 8.482916 0.36 0.36 -5.60388469+ 8.482916i
#> 20 -6.00610128 8.958980 0.38 0.38 -6.00610128+ 8.958980i
#> 21 -6.28438335 9.359339 0.40 0.40 -6.28438335+ 9.359339i
#> 22 -6.56257383 9.786869 0.42 0.42 -6.56257383+ 9.786869i
#> 23 -6.82829950 10.211682 0.44 0.44 -6.82829950+10.211682i
#> 24 -7.12725102 10.651670 0.46 0.46 -7.12725102+10.651670i
#> 25 -7.43344776 11.163500 0.48 0.48 -7.43344776+11.163500i
#> 26 -7.64290043 11.561354 0.50 0.50 -7.64290043+11.561354i
#> 27 -7.86061218 12.000399 0.52 0.52 -7.86061218+12.000399i
#> 28 -8.07877827 12.440758 0.54 0.54 -8.07877827+12.440758i
#> 29 -8.31433386 12.895866 0.56 0.56 -8.31433386+12.895866i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_1 Sim_3 TrajSim_1_3
#> 2 -0.3691512+0.4146643i Traj_1 Sim_3 TrajSim_1_3
#> 3 -0.3635283+0.4299940i Traj_1 Sim_3 TrajSim_1_3
#> 4 -0.3642538+0.4389412i Traj_1 Sim_3 TrajSim_1_3
#> 5 -0.3957117+0.4337989i Traj_1 Sim_3 TrajSim_1_3
#> 6 -0.4179590+0.5063028i Traj_1 Sim_3 TrajSim_1_3
#> 7 -0.3468765+0.3955273i Traj_1 Sim_3 TrajSim_1_3
#> 8 -0.4083926+0.4832861i Traj_1 Sim_3 TrajSim_1_3
#> 9 -0.3434065+0.4593451i Traj_1 Sim_3 TrajSim_1_3
#> 10 -0.2868134+0.3530652i Traj_1 Sim_3 TrajSim_1_3
#> 11 -0.2648548+0.2871004i Traj_1 Sim_3 TrajSim_1_3
#> 12 -0.3922091+0.4477882i Traj_1 Sim_3 TrajSim_1_3
#> 13 -0.3794923+0.4675649i Traj_1 Sim_3 TrajSim_1_3
#> 14 -0.4112822+0.4570094i Traj_1 Sim_3 TrajSim_1_3
#> 15 -0.3120364+0.4063179i Traj_1 Sim_3 TrajSim_1_3
#> 16 -0.3194998+0.4064769i Traj_1 Sim_3 TrajSim_1_3
#> 17 -0.3225629+0.3687840i Traj_1 Sim_3 TrajSim_1_3
#> 18 -0.2537205+0.3465262i Traj_1 Sim_3 TrajSim_1_3
#> 19 -0.3481337+0.4344229i Traj_1 Sim_3 TrajSim_1_3
#> 20 -0.4022166+0.4760644i Traj_1 Sim_3 TrajSim_1_3
#> 21 -0.2782821+0.4003586i Traj_1 Sim_3 TrajSim_1_3
#> 22 -0.2781905+0.4275300i Traj_1 Sim_3 TrajSim_1_3
#> 23 -0.2657257+0.4248132i Traj_1 Sim_3 TrajSim_1_3
#> 24 -0.2989515+0.4399879i Traj_1 Sim_3 TrajSim_1_3
#> 25 -0.3061967+0.5118306i Traj_1 Sim_3 TrajSim_1_3
#> 26 -0.2094527+0.3978540i Traj_1 Sim_3 TrajSim_1_3
#> 27 -0.2177118+0.4390445i Traj_1 Sim_3 TrajSim_1_3
#> 28 -0.2181661+0.4403592i Traj_1 Sim_3 TrajSim_1_3
#> 29 -0.2355556+0.4551076i Traj_1 Sim_3 TrajSim_1_3
#>
#> [[3]][[2]]
#> x y time displacementTime polar
#> 1 0.33600000 1.5600000 0.00 0.00 0.33600000+ 1.5600000i
#> 2 0.37302094 0.8709972 0.02 0.02 0.37302094+ 0.8709972i
#> 3 0.33286949 0.2692799 0.04 0.04 0.33286949+ 0.2692799i
#> 4 0.36888728 -0.3661295 0.06 0.06 0.36888728- 0.3661295i
#> 5 0.41400565 -0.9868769 0.08 0.08 0.41400565- 0.9868769i
#> 6 0.48445595 -1.5738119 0.10 0.10 0.48445595- 1.5738119i
#> 7 0.56400348 -2.1996521 0.12 0.12 0.56400348- 2.1996521i
#> 8 0.59380828 -2.7157237 0.14 0.14 0.59380828- 2.7157237i
#> 9 0.65609163 -3.4392147 0.16 0.16 0.65609163- 3.4392147i
#> 10 0.48700858 -4.1109230 0.18 0.18 0.48700858- 4.1109230i
#> 11 0.28134018 -4.6508585 0.20 0.20 0.28134018- 4.6508585i
#> 12 0.14848322 -5.0871147 0.22 0.22 0.14848322- 5.0871147i
#> 13 0.03128061 -5.6501372 0.24 0.24 0.03128061- 5.6501372i
#> 14 -0.05180552 -6.1445709 0.26 0.26 -0.05180552- 6.1445709i
#> 15 -0.12843112 -6.6056208 0.28 0.28 -0.12843112- 6.6056208i
#> 16 -0.14881638 -7.0901744 0.30 0.30 -0.14881638- 7.0901744i
#> 17 -0.13325714 -7.7838089 0.32 0.32 -0.13325714- 7.7838089i
#> 18 -0.08725468 -8.5097976 0.34 0.34 -0.08725468- 8.5097976i
#> 19 -0.11396700 -9.1031248 0.36 0.36 -0.11396700- 9.1031248i
#> 20 -0.06694136 -9.6764070 0.38 0.38 -0.06694136- 9.6764070i
#> 21 0.03032684 -10.3083524 0.40 0.40 0.03032684-10.3083524i
#> 22 0.09911121 -10.9043637 0.42 0.42 0.09911121-10.9043637i
#> 23 0.23100616 -11.5072737 0.44 0.44 0.23100616-11.5072737i
#> 24 0.24337361 -12.1796957 0.46 0.46 0.24337361-12.1796957i
#> displacement Trajectory Simulation TrajSim
#> 1 0.00000000+0.0000000i Traj_2 Sim_3 TrajSim_2_3
#> 2 0.03702094-0.6890028i Traj_2 Sim_3 TrajSim_2_3
#> 3 -0.04015145-0.6017173i Traj_2 Sim_3 TrajSim_2_3
#> 4 0.03601779-0.6354094i Traj_2 Sim_3 TrajSim_2_3
#> 5 0.04511838-0.6207473i Traj_2 Sim_3 TrajSim_2_3
#> 6 0.07045030-0.5869350i Traj_2 Sim_3 TrajSim_2_3
#> 7 0.07954753-0.6258402i Traj_2 Sim_3 TrajSim_2_3
#> 8 0.02980480-0.5160716i Traj_2 Sim_3 TrajSim_2_3
#> 9 0.06228335-0.7234910i Traj_2 Sim_3 TrajSim_2_3
#> 10 -0.16908305-0.6717083i Traj_2 Sim_3 TrajSim_2_3
#> 11 -0.20566840-0.5399355i Traj_2 Sim_3 TrajSim_2_3
#> 12 -0.13285696-0.4362562i Traj_2 Sim_3 TrajSim_2_3
#> 13 -0.11720261-0.5630225i Traj_2 Sim_3 TrajSim_2_3
#> 14 -0.08308613-0.4944338i Traj_2 Sim_3 TrajSim_2_3
#> 15 -0.07662560-0.4610498i Traj_2 Sim_3 TrajSim_2_3
#> 16 -0.02038525-0.4845536i Traj_2 Sim_3 TrajSim_2_3
#> 17 0.01555924-0.6936345i Traj_2 Sim_3 TrajSim_2_3
#> 18 0.04600245-0.7259888i Traj_2 Sim_3 TrajSim_2_3
#> 19 -0.02671232-0.5933272i Traj_2 Sim_3 TrajSim_2_3
#> 20 0.04702564-0.5732822i Traj_2 Sim_3 TrajSim_2_3
#> 21 0.09726820-0.6319454i Traj_2 Sim_3 TrajSim_2_3
#> 22 0.06878438-0.5960114i Traj_2 Sim_3 TrajSim_2_3
#> 23 0.13189495-0.6029100i Traj_2 Sim_3 TrajSim_2_3
#> 24 0.01236745-0.6724220i Traj_2 Sim_3 TrajSim_2_3
#>
#>
#> [[4]]
#> [[4]][[1]]
#> x y time displacementTime polar
#> 1 0.6960000 0.946000 0.00 0.00 0.6960000+0.946000i
#> 2 0.2013268 1.285468 0.02 0.02 0.2013268+1.285468i
#> 3 -0.2143578 1.641297 0.04 0.04 -0.2143578+1.641297i
#> 4 -0.5935370 1.953709 0.06 0.06 -0.5935370+1.953709i
#> 5 -1.0253562 2.260607 0.08 0.08 -1.0253562+2.260607i
#> 6 -1.4374265 2.627487 0.10 0.10 -1.4374265+2.627487i
#> 7 -1.8738876 2.992109 0.12 0.12 -1.8738876+2.992109i
#> 8 -2.2421374 3.308143 0.14 0.14 -2.2421374+3.308143i
#> 9 -2.6414540 3.635480 0.16 0.16 -2.6414540+3.635480i
#> 10 -3.0312100 3.988109 0.18 0.18 -3.0312100+3.988109i
#> 11 -3.4713580 4.350435 0.20 0.20 -3.4713580+4.350435i
#> 12 -3.9291515 4.733370 0.22 0.22 -3.9291515+4.733370i
#> 13 -4.3357913 5.020649 0.24 0.24 -4.3357913+5.020649i
#> 14 -4.8742937 5.378101 0.26 0.26 -4.8742937+5.378101i
#> 15 -5.4194957 5.754400 0.28 0.28 -5.4194957+5.754400i
#> 16 -5.8310583 6.013860 0.30 0.30 -5.8310583+6.013860i
#> 17 -6.2660660 6.297047 0.32 0.32 -6.2660660+6.297047i
#> 18 -6.6643958 6.580707 0.34 0.34 -6.6643958+6.580707i
#> 19 -7.1748574 6.961237 0.36 0.36 -7.1748574+6.961237i
#> 20 -7.5930516 7.296763 0.38 0.38 -7.5930516+7.296763i
#> 21 -8.0001556 7.562556 0.40 0.40 -8.0001556+7.562556i
#> 22 -8.4265733 7.809185 0.42 0.42 -8.4265733+7.809185i
#> 23 -8.9340495 8.042157 0.44 0.44 -8.9340495+8.042157i
#> 24 -9.4245061 8.296952 0.46 0.46 -9.4245061+8.296952i
#> 25 -9.9275228 8.563178 0.48 0.48 -9.9275228+8.563178i
#> 26 -10.3936085 8.832873 0.50 0.50 -10.3936085+8.832873i
#> 27 -10.8089091 9.022030 0.52 0.52 -10.8089091+9.022030i
#> 28 -11.3972277 9.268932 0.54 0.54 -11.3972277+9.268932i
#> 29 -11.8898116 9.501156 0.56 0.56 -11.8898116+9.501156i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_1 Sim_4 TrajSim_1_4
#> 2 -0.4946732+0.3394682i Traj_1 Sim_4 TrajSim_1_4
#> 3 -0.4156846+0.3558283i Traj_1 Sim_4 TrajSim_1_4
#> 4 -0.3791793+0.3124125i Traj_1 Sim_4 TrajSim_1_4
#> 5 -0.4318192+0.3068984i Traj_1 Sim_4 TrajSim_1_4
#> 6 -0.4120703+0.3668796i Traj_1 Sim_4 TrajSim_1_4
#> 7 -0.4364611+0.3646217i Traj_1 Sim_4 TrajSim_1_4
#> 8 -0.3682498+0.3160347i Traj_1 Sim_4 TrajSim_1_4
#> 9 -0.3993166+0.3273368i Traj_1 Sim_4 TrajSim_1_4
#> 10 -0.3897560+0.3526289i Traj_1 Sim_4 TrajSim_1_4
#> 11 -0.4401480+0.3623255i Traj_1 Sim_4 TrajSim_1_4
#> 12 -0.4577936+0.3829355i Traj_1 Sim_4 TrajSim_1_4
#> 13 -0.4066398+0.2872792i Traj_1 Sim_4 TrajSim_1_4
#> 14 -0.5385023+0.3574517i Traj_1 Sim_4 TrajSim_1_4
#> 15 -0.5452021+0.3762990i Traj_1 Sim_4 TrajSim_1_4
#> 16 -0.4115626+0.2594595i Traj_1 Sim_4 TrajSim_1_4
#> 17 -0.4350077+0.2831874i Traj_1 Sim_4 TrajSim_1_4
#> 18 -0.3983299+0.2836605i Traj_1 Sim_4 TrajSim_1_4
#> 19 -0.5104616+0.3805296i Traj_1 Sim_4 TrajSim_1_4
#> 20 -0.4181941+0.3355265i Traj_1 Sim_4 TrajSim_1_4
#> 21 -0.4071041+0.2657925i Traj_1 Sim_4 TrajSim_1_4
#> 22 -0.4264177+0.2466287i Traj_1 Sim_4 TrajSim_1_4
#> 23 -0.5074761+0.2329722i Traj_1 Sim_4 TrajSim_1_4
#> 24 -0.4904567+0.2547948i Traj_1 Sim_4 TrajSim_1_4
#> 25 -0.5030167+0.2662261i Traj_1 Sim_4 TrajSim_1_4
#> 26 -0.4660857+0.2696952i Traj_1 Sim_4 TrajSim_1_4
#> 27 -0.4153006+0.1891572i Traj_1 Sim_4 TrajSim_1_4
#> 28 -0.5883186+0.2469021i Traj_1 Sim_4 TrajSim_1_4
#> 29 -0.4925839+0.2322234i Traj_1 Sim_4 TrajSim_1_4
#>
#> [[4]][[2]]
#> x y time displacementTime polar
#> 1 0.33600000 1.560000 0.00 0.00 0.33600000+ 1.560000i
#> 2 0.13949617 2.241386 0.02 0.02 0.13949617+ 2.241386i
#> 3 0.02065731 2.869680 0.04 0.04 0.02065731+ 2.869680i
#> 4 -0.05299513 3.490581 0.06 0.06 -0.05299513+ 3.490581i
#> 5 -0.06528095 4.109258 0.08 0.08 -0.06528095+ 4.109258i
#> 6 -0.18084374 4.732513 0.10 0.10 -0.18084374+ 4.732513i
#> 7 -0.28434634 5.244621 0.12 0.12 -0.28434634+ 5.244621i
#> 8 -0.46471847 5.962644 0.14 0.14 -0.46471847+ 5.962644i
#> 9 -0.58907927 6.516915 0.16 0.16 -0.58907927+ 6.516915i
#> 10 -0.70339046 6.990403 0.18 0.18 -0.70339046+ 6.990403i
#> 11 -0.82576660 7.564237 0.20 0.20 -0.82576660+ 7.564237i
#> 12 -1.10448199 8.099526 0.22 0.22 -1.10448199+ 8.099526i
#> 13 -1.42167115 8.681549 0.24 0.24 -1.42167115+ 8.681549i
#> 14 -1.59652248 9.127918 0.26 0.26 -1.59652248+ 9.127918i
#> 15 -1.76842736 9.633258 0.28 0.28 -1.76842736+ 9.633258i
#> 16 -1.99337015 10.291216 0.30 0.30 -1.99337015+10.291216i
#> 17 -2.27744517 10.883048 0.32 0.32 -2.27744517+10.883048i
#> 18 -2.54424011 11.403586 0.34 0.34 -2.54424011+11.403586i
#> 19 -2.96455610 11.964756 0.36 0.36 -2.96455610+11.964756i
#> 20 -3.41292532 12.517738 0.38 0.38 -3.41292532+12.517738i
#> 21 -3.81560966 13.047045 0.40 0.40 -3.81560966+13.047045i
#> 22 -4.27559487 13.490935 0.42 0.42 -4.27559487+13.490935i
#> 23 -4.53842533 13.785414 0.44 0.44 -4.53842533+13.785414i
#> 24 -4.87419004 14.212320 0.46 0.46 -4.87419004+14.212320i
#> displacement Trajectory Simulation TrajSim
#> 1 0.00000000+0.0000000i Traj_2 Sim_4 TrajSim_2_4
#> 2 -0.19650383+0.6813857i Traj_2 Sim_4 TrajSim_2_4
#> 3 -0.11883886+0.6282944i Traj_2 Sim_4 TrajSim_2_4
#> 4 -0.07365244+0.6209009i Traj_2 Sim_4 TrajSim_2_4
#> 5 -0.01228582+0.6186772i Traj_2 Sim_4 TrajSim_2_4
#> 6 -0.11556279+0.6232552i Traj_2 Sim_4 TrajSim_2_4
#> 7 -0.10350260+0.5121079i Traj_2 Sim_4 TrajSim_2_4
#> 8 -0.18037212+0.7180222i Traj_2 Sim_4 TrajSim_2_4
#> 9 -0.12436080+0.5542718i Traj_2 Sim_4 TrajSim_2_4
#> 10 -0.11431119+0.4734879i Traj_2 Sim_4 TrajSim_2_4
#> 11 -0.12237614+0.5738341i Traj_2 Sim_4 TrajSim_2_4
#> 12 -0.27871539+0.5352884i Traj_2 Sim_4 TrajSim_2_4
#> 13 -0.31718916+0.5820237i Traj_2 Sim_4 TrajSim_2_4
#> 14 -0.17485133+0.4463684i Traj_2 Sim_4 TrajSim_2_4
#> 15 -0.17190488+0.5053403i Traj_2 Sim_4 TrajSim_2_4
#> 16 -0.22494279+0.6579575i Traj_2 Sim_4 TrajSim_2_4
#> 17 -0.28407502+0.5918326i Traj_2 Sim_4 TrajSim_2_4
#> 18 -0.26679494+0.5205377i Traj_2 Sim_4 TrajSim_2_4
#> 19 -0.42031599+0.5611696i Traj_2 Sim_4 TrajSim_2_4
#> 20 -0.44836922+0.5529823i Traj_2 Sim_4 TrajSim_2_4
#> 21 -0.40268434+0.5293068i Traj_2 Sim_4 TrajSim_2_4
#> 22 -0.45998521+0.4438909i Traj_2 Sim_4 TrajSim_2_4
#> 23 -0.26283046+0.2944787i Traj_2 Sim_4 TrajSim_2_4
#> 24 -0.33576471+0.4269062i Traj_2 Sim_4 TrajSim_2_4
#>
#>
#> [[5]]
#> [[5]][[1]]
#> x y time displacementTime polar
#> 1 0.696000 0.946000 0.00 0.00 0.696000+ 0.946000i
#> 2 1.076287 1.238101 0.02 0.02 1.076287+ 1.238101i
#> 3 1.503106 1.616717 0.04 0.04 1.503106+ 1.616717i
#> 4 1.988618 2.051913 0.06 0.06 1.988618+ 2.051913i
#> 5 2.375166 2.450171 0.08 0.08 2.375166+ 2.450171i
#> 6 2.735799 2.857681 0.10 0.10 2.735799+ 2.857681i
#> 7 3.059595 3.261982 0.12 0.12 3.059595+ 3.261982i
#> 8 3.320789 3.593522 0.14 0.14 3.320789+ 3.593522i
#> 9 3.648857 4.065779 0.16 0.16 3.648857+ 4.065779i
#> 10 3.907511 4.504792 0.18 0.18 3.907511+ 4.504792i
#> 11 4.180615 5.066532 0.20 0.20 4.180615+ 5.066532i
#> 12 4.489899 5.561326 0.22 0.22 4.489899+ 5.561326i
#> 13 4.796232 6.016322 0.24 0.24 4.796232+ 6.016322i
#> 14 5.126106 6.375855 0.26 0.26 5.126106+ 6.375855i
#> 15 5.489558 6.795821 0.28 0.28 5.489558+ 6.795821i
#> 16 5.813669 7.214952 0.30 0.30 5.813669+ 7.214952i
#> 17 6.096180 7.602113 0.32 0.32 6.096180+ 7.602113i
#> 18 6.402569 8.034025 0.34 0.34 6.402569+ 8.034025i
#> 19 6.632573 8.379538 0.36 0.36 6.632573+ 8.379538i
#> 20 6.927086 8.802001 0.38 0.38 6.927086+ 8.802001i
#> 21 7.218665 9.256714 0.40 0.40 7.218665+ 9.256714i
#> 22 7.481700 9.759939 0.42 0.42 7.481700+ 9.759939i
#> 23 7.705623 10.178253 0.44 0.44 7.705623+10.178253i
#> 24 7.958324 10.596708 0.46 0.46 7.958324+10.596708i
#> 25 8.243712 11.067635 0.48 0.48 8.243712+11.067635i
#> 26 8.605053 11.546710 0.50 0.50 8.605053+11.546710i
#> 27 8.940434 12.054626 0.52 0.52 8.940434+12.054626i
#> 28 9.196022 12.536101 0.54 0.54 9.196022+12.536101i
#> 29 9.434420 13.016546 0.56 0.56 9.434420+13.016546i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_1 Sim_5 TrajSim_1_5
#> 2 0.3802868+0.2921009i Traj_1 Sim_5 TrajSim_1_5
#> 3 0.4268187+0.3786159i Traj_1 Sim_5 TrajSim_1_5
#> 4 0.4855121+0.4351963i Traj_1 Sim_5 TrajSim_1_5
#> 5 0.3865483+0.3982581i Traj_1 Sim_5 TrajSim_1_5
#> 6 0.3606328+0.4075102i Traj_1 Sim_5 TrajSim_1_5
#> 7 0.3237958+0.4043011i Traj_1 Sim_5 TrajSim_1_5
#> 8 0.2611940+0.3315392i Traj_1 Sim_5 TrajSim_1_5
#> 9 0.3280682+0.4722571i Traj_1 Sim_5 TrajSim_1_5
#> 10 0.2586544+0.4390137i Traj_1 Sim_5 TrajSim_1_5
#> 11 0.2731040+0.5617400i Traj_1 Sim_5 TrajSim_1_5
#> 12 0.3092836+0.4947936i Traj_1 Sim_5 TrajSim_1_5
#> 13 0.3063328+0.4549960i Traj_1 Sim_5 TrajSim_1_5
#> 14 0.3298742+0.3595327i Traj_1 Sim_5 TrajSim_1_5
#> 15 0.3634523+0.4199664i Traj_1 Sim_5 TrajSim_1_5
#> 16 0.3241109+0.4191307i Traj_1 Sim_5 TrajSim_1_5
#> 17 0.2825108+0.3871613i Traj_1 Sim_5 TrajSim_1_5
#> 18 0.3063897+0.4319120i Traj_1 Sim_5 TrajSim_1_5
#> 19 0.2300039+0.3455132i Traj_1 Sim_5 TrajSim_1_5
#> 20 0.2945124+0.4224628i Traj_1 Sim_5 TrajSim_1_5
#> 21 0.2915792+0.4547127i Traj_1 Sim_5 TrajSim_1_5
#> 22 0.2630347+0.5032255i Traj_1 Sim_5 TrajSim_1_5
#> 23 0.2239229+0.4183139i Traj_1 Sim_5 TrajSim_1_5
#> 24 0.2527009+0.4184546i Traj_1 Sim_5 TrajSim_1_5
#> 25 0.2853881+0.4709271i Traj_1 Sim_5 TrajSim_1_5
#> 26 0.3613415+0.4790750i Traj_1 Sim_5 TrajSim_1_5
#> 27 0.3353807+0.5079162i Traj_1 Sim_5 TrajSim_1_5
#> 28 0.2555886+0.4814750i Traj_1 Sim_5 TrajSim_1_5
#> 29 0.2383971+0.4804454i Traj_1 Sim_5 TrajSim_1_5
#>
#> [[5]][[2]]
#> x y time displacementTime polar
#> 1 0.3360000 1.560000 0.00 0.00 0.3360000+1.560000i
#> 2 -0.3161689 1.540026 0.02 0.02 -0.3161689+1.540026i
#> 3 -1.0679872 1.555078 0.04 0.04 -1.0679872+1.555078i
#> 4 -1.7922421 1.570468 0.06 0.06 -1.7922421+1.570468i
#> 5 -2.4881707 1.561334 0.08 0.08 -2.4881707+1.561334i
#> 6 -3.1824756 1.772573 0.10 0.10 -3.1824756+1.772573i
#> 7 -3.8577381 1.877358 0.12 0.12 -3.8577381+1.877358i
#> 8 -4.4454932 1.992580 0.14 0.14 -4.4454932+1.992580i
#> 9 -5.1257228 2.083052 0.16 0.16 -5.1257228+2.083052i
#> 10 -5.7201237 2.158938 0.18 0.18 -5.7201237+2.158938i
#> 11 -6.4088307 2.203344 0.20 0.20 -6.4088307+2.203344i
#> 12 -7.0153284 2.238271 0.22 0.22 -7.0153284+2.238271i
#> 13 -7.6022751 2.239873 0.24 0.24 -7.6022751+2.239873i
#> 14 -8.3401285 2.284627 0.26 0.26 -8.3401285+2.284627i
#> 15 -9.0240434 2.416507 0.28 0.28 -9.0240434+2.416507i
#> 16 -9.5282866 2.592995 0.30 0.30 -9.5282866+2.592995i
#> 17 -10.0044488 2.874278 0.32 0.32 -10.0044488+2.874278i
#> 18 -10.4986170 3.189774 0.34 0.34 -10.4986170+3.189774i
#> 19 -11.1315903 3.483189 0.36 0.36 -11.1315903+3.483189i
#> 20 -11.5621445 3.721378 0.38 0.38 -11.5621445+3.721378i
#> 21 -12.1093935 3.943920 0.40 0.40 -12.1093935+3.943920i
#> 22 -12.6715493 4.154686 0.42 0.42 -12.6715493+4.154686i
#> 23 -13.2212576 4.384421 0.44 0.44 -13.2212576+4.384421i
#> 24 -13.7220786 4.558012 0.46 0.46 -13.7220786+4.558012i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.000000000i Traj_2 Sim_5 TrajSim_2_5
#> 2 -0.6521689-0.019973738i Traj_2 Sim_5 TrajSim_2_5
#> 3 -0.7518183+0.015052144i Traj_2 Sim_5 TrajSim_2_5
#> 4 -0.7242549+0.015389975i Traj_2 Sim_5 TrajSim_2_5
#> 5 -0.6959286-0.009134663i Traj_2 Sim_5 TrajSim_2_5
#> 6 -0.6943049+0.211239374i Traj_2 Sim_5 TrajSim_2_5
#> 7 -0.6752625+0.104785281i Traj_2 Sim_5 TrajSim_2_5
#> 8 -0.5877551+0.115221591i Traj_2 Sim_5 TrajSim_2_5
#> 9 -0.6802296+0.090471937i Traj_2 Sim_5 TrajSim_2_5
#> 10 -0.5944009+0.075885736i Traj_2 Sim_5 TrajSim_2_5
#> 11 -0.6887070+0.044405949i Traj_2 Sim_5 TrajSim_2_5
#> 12 -0.6064977+0.034927340i Traj_2 Sim_5 TrajSim_2_5
#> 13 -0.5869467+0.001602191i Traj_2 Sim_5 TrajSim_2_5
#> 14 -0.7378533+0.044753584i Traj_2 Sim_5 TrajSim_2_5
#> 15 -0.6839149+0.131880083i Traj_2 Sim_5 TrajSim_2_5
#> 16 -0.5042433+0.176488470i Traj_2 Sim_5 TrajSim_2_5
#> 17 -0.4761622+0.281282406i Traj_2 Sim_5 TrajSim_2_5
#> 18 -0.4941682+0.315496535i Traj_2 Sim_5 TrajSim_2_5
#> 19 -0.6329734+0.293414956i Traj_2 Sim_5 TrajSim_2_5
#> 20 -0.4305541+0.238188652i Traj_2 Sim_5 TrajSim_2_5
#> 21 -0.5472490+0.222541963i Traj_2 Sim_5 TrajSim_2_5
#> 22 -0.5621558+0.210765961i Traj_2 Sim_5 TrajSim_2_5
#> 23 -0.5497083+0.229735421i Traj_2 Sim_5 TrajSim_2_5
#> 24 -0.5008209+0.173590568i Traj_2 Sim_5 TrajSim_2_5
#>
#>
#> [[6]]
#> [[6]][[1]]
#> x y time displacementTime polar
#> 1 6.960000e-01 0.9460000 0.00 0.00 6.960000e-01+ 0.9460000i
#> 2 7.178134e-01 0.4038728 0.02 0.02 7.178134e-01+ 0.4038728i
#> 3 7.821149e-01 -0.1195903 0.04 0.04 7.821149e-01- 0.1195903i
#> 4 8.589146e-01 -0.5815207 0.06 0.06 8.589146e-01- 0.5815207i
#> 5 9.285354e-01 -1.0797385 0.08 0.08 9.285354e-01- 1.0797385i
#> 6 9.307036e-01 -1.6687757 0.10 0.10 9.307036e-01- 1.6687757i
#> 7 9.778395e-01 -2.1967871 0.12 0.12 9.778395e-01- 2.1967871i
#> 8 1.016713e+00 -2.7911850 0.14 0.14 1.016713e+00- 2.7911850i
#> 9 1.022836e+00 -3.3124453 0.16 0.16 1.022836e+00- 3.3124453i
#> 10 9.312325e-01 -3.8983537 0.18 0.18 9.312325e-01- 3.8983537i
#> 11 8.488722e-01 -4.4670699 0.20 0.20 8.488722e-01- 4.4670699i
#> 12 6.724098e-01 -5.0531520 0.22 0.22 6.724098e-01- 5.0531520i
#> 13 5.757461e-01 -5.5179001 0.24 0.24 5.757461e-01- 5.5179001i
#> 14 4.325148e-01 -6.0479575 0.26 0.26 4.325148e-01- 6.0479575i
#> 15 3.090777e-01 -6.5819563 0.28 0.28 3.090777e-01- 6.5819563i
#> 16 2.179213e-01 -7.1749038 0.30 0.30 2.179213e-01- 7.1749038i
#> 17 1.930160e-01 -7.6900189 0.32 0.32 1.930160e-01- 7.6900189i
#> 18 1.470147e-01 -8.2969359 0.34 0.34 1.470147e-01- 8.2969359i
#> 19 1.492842e-01 -8.7519156 0.36 0.36 1.492842e-01- 8.7519156i
#> 20 8.984935e-02 -9.1857815 0.38 0.38 8.984935e-02- 9.1857815i
#> 21 -5.779876e-05 -9.7022894 0.40 0.40 -5.779876e-05- 9.7022894i
#> 22 -6.756561e-02 -10.1968231 0.42 0.42 -6.756561e-02-10.1968231i
#> 23 -1.313512e-01 -10.7327226 0.44 0.44 -1.313512e-01-10.7327226i
#> 24 -2.277354e-01 -11.2398120 0.46 0.46 -2.277354e-01-11.2398120i
#> 25 -3.176865e-01 -11.8176190 0.48 0.48 -3.176865e-01-11.8176190i
#> 26 -4.082198e-01 -12.3792098 0.50 0.50 -4.082198e-01-12.3792098i
#> 27 -5.084674e-01 -12.9256207 0.52 0.52 -5.084674e-01-12.9256207i
#> 28 -6.075876e-01 -13.4298360 0.54 0.54 -6.075876e-01-13.4298360i
#> 29 -6.436104e-01 -13.9390373 0.56 0.56 -6.436104e-01-13.9390373i
#> displacement Trajectory Simulation TrajSim
#> 1 0.000000000+0.0000000i Traj_1 Sim_6 TrajSim_1_6
#> 2 0.021813409-0.5421272i Traj_1 Sim_6 TrajSim_1_6
#> 3 0.064301533-0.5234631i Traj_1 Sim_6 TrajSim_1_6
#> 4 0.076799621-0.4619305i Traj_1 Sim_6 TrajSim_1_6
#> 5 0.069620883-0.4982178i Traj_1 Sim_6 TrajSim_1_6
#> 6 0.002168130-0.5890371i Traj_1 Sim_6 TrajSim_1_6
#> 7 0.047135973-0.5280115i Traj_1 Sim_6 TrajSim_1_6
#> 8 0.038873413-0.5943979i Traj_1 Sim_6 TrajSim_1_6
#> 9 0.006122822-0.5212603i Traj_1 Sim_6 TrajSim_1_6
#> 10 -0.091603253-0.5859084i Traj_1 Sim_6 TrajSim_1_6
#> 11 -0.082360380-0.5687162i Traj_1 Sim_6 TrajSim_1_6
#> 12 -0.176462363-0.5860821i Traj_1 Sim_6 TrajSim_1_6
#> 13 -0.096663725-0.4647480i Traj_1 Sim_6 TrajSim_1_6
#> 14 -0.143231236-0.5300574i Traj_1 Sim_6 TrajSim_1_6
#> 15 -0.123437125-0.5339989i Traj_1 Sim_6 TrajSim_1_6
#> 16 -0.091156414-0.5929474i Traj_1 Sim_6 TrajSim_1_6
#> 17 -0.024905287-0.5151152i Traj_1 Sim_6 TrajSim_1_6
#> 18 -0.046001324-0.6069170i Traj_1 Sim_6 TrajSim_1_6
#> 19 0.002269494-0.4549797i Traj_1 Sim_6 TrajSim_1_6
#> 20 -0.059434820-0.4338659i Traj_1 Sim_6 TrajSim_1_6
#> 21 -0.089907151-0.5165078i Traj_1 Sim_6 TrajSim_1_6
#> 22 -0.067507812-0.4945338i Traj_1 Sim_6 TrajSim_1_6
#> 23 -0.063785611-0.5358995i Traj_1 Sim_6 TrajSim_1_6
#> 24 -0.096384128-0.5070895i Traj_1 Sim_6 TrajSim_1_6
#> 25 -0.089951194-0.5778070i Traj_1 Sim_6 TrajSim_1_6
#> 26 -0.090533233-0.5615908i Traj_1 Sim_6 TrajSim_1_6
#> 27 -0.100247591-0.5464109i Traj_1 Sim_6 TrajSim_1_6
#> 28 -0.099120271-0.5042153i Traj_1 Sim_6 TrajSim_1_6
#> 29 -0.036022768-0.5092013i Traj_1 Sim_6 TrajSim_1_6
#>
#> [[6]][[2]]
#> x y time displacementTime polar
#> 1 0.3360000 1.5600000 0.00 0.00 0.3360000+ 1.5600000i
#> 2 0.7886211 1.0796926 0.02 0.02 0.7886211+ 1.0796926i
#> 3 1.2110698 0.6615922 0.04 0.04 1.2110698+ 0.6615922i
#> 4 1.7607917 0.2207274 0.06 0.06 1.7607917+ 0.2207274i
#> 5 2.2977642 -0.3300578 0.08 0.08 2.2977642- 0.3300578i
#> 6 2.5887705 -0.7296834 0.10 0.10 2.5887705- 0.7296834i
#> 7 2.8343876 -1.2201853 0.12 0.12 2.8343876- 1.2201853i
#> 8 3.1066809 -1.8717024 0.14 0.14 3.1066809- 1.8717024i
#> 9 3.2915680 -2.5221269 0.16 0.16 3.2915680- 2.5221269i
#> 10 3.3610044 -3.0264102 0.18 0.18 3.3610044- 3.0264102i
#> 11 3.4136214 -3.6370662 0.20 0.20 3.4136214- 3.6370662i
#> 12 3.3640781 -4.2966970 0.22 0.22 3.3640781- 4.2966970i
#> 13 3.2113762 -4.8657895 0.24 0.24 3.2113762- 4.8657895i
#> 14 2.8940751 -5.4118302 0.26 0.26 2.8940751- 5.4118302i
#> 15 2.6183522 -5.9088698 0.28 0.28 2.6183522- 5.9088698i
#> 16 2.3292621 -6.3901645 0.30 0.30 2.3292621- 6.3901645i
#> 17 1.9273264 -6.9692573 0.32 0.32 1.9273264- 6.9692573i
#> 18 1.6020191 -7.5259656 0.34 0.34 1.6020191- 7.5259656i
#> 19 1.3396757 -8.0364729 0.36 0.36 1.3396757- 8.0364729i
#> 20 1.1027808 -8.5461931 0.38 0.38 1.1027808- 8.5461931i
#> 21 0.8974188 -9.0364341 0.40 0.40 0.8974188- 9.0364341i
#> 22 0.7225779 -9.6863022 0.42 0.42 0.7225779- 9.6863022i
#> 23 0.5443814 -10.2923804 0.44 0.44 0.5443814-10.2923804i
#> 24 0.4624215 -10.8867057 0.46 0.46 0.4624215-10.8867057i
#> displacement Trajectory Simulation TrajSim
#> 1 0.00000000+0.0000000i Traj_2 Sim_6 TrajSim_2_6
#> 2 0.45262110-0.4803074i Traj_2 Sim_6 TrajSim_2_6
#> 3 0.42244866-0.4181004i Traj_2 Sim_6 TrajSim_2_6
#> 4 0.54972192-0.4408648i Traj_2 Sim_6 TrajSim_2_6
#> 5 0.53697255-0.5507852i Traj_2 Sim_6 TrajSim_2_6
#> 6 0.29100627-0.3996256i Traj_2 Sim_6 TrajSim_2_6
#> 7 0.24561706-0.4905019i Traj_2 Sim_6 TrajSim_2_6
#> 8 0.27229338-0.6515171i Traj_2 Sim_6 TrajSim_2_6
#> 9 0.18488705-0.6504246i Traj_2 Sim_6 TrajSim_2_6
#> 10 0.06943646-0.5042832i Traj_2 Sim_6 TrajSim_2_6
#> 11 0.05261694-0.6106560i Traj_2 Sim_6 TrajSim_2_6
#> 12 -0.04954329-0.6596308i Traj_2 Sim_6 TrajSim_2_6
#> 13 -0.15270190-0.5690925i Traj_2 Sim_6 TrajSim_2_6
#> 14 -0.31730109-0.5460407i Traj_2 Sim_6 TrajSim_2_6
#> 15 -0.27572292-0.4970396i Traj_2 Sim_6 TrajSim_2_6
#> 16 -0.28909005-0.4812947i Traj_2 Sim_6 TrajSim_2_6
#> 17 -0.40193570-0.5790927i Traj_2 Sim_6 TrajSim_2_6
#> 18 -0.32530733-0.5567083i Traj_2 Sim_6 TrajSim_2_6
#> 19 -0.26234343-0.5105073i Traj_2 Sim_6 TrajSim_2_6
#> 20 -0.23689490-0.5097202i Traj_2 Sim_6 TrajSim_2_6
#> 21 -0.20536194-0.4902410i Traj_2 Sim_6 TrajSim_2_6
#> 22 -0.17484092-0.6498680i Traj_2 Sim_6 TrajSim_2_6
#> 23 -0.17819646-0.6060782i Traj_2 Sim_6 TrajSim_2_6
#> 24 -0.08195994-0.5943253i Traj_2 Sim_6 TrajSim_2_6
#>
#>
#> [[7]]
#> [[7]][[1]]
#> x y time displacementTime polar
#> 1 0.6960000 0.946000 0.00 0.00 0.6960000+0.946000i
#> 2 0.2236459 1.205100 0.02 0.02 0.2236459+1.205100i
#> 3 -0.1638811 1.430154 0.04 0.04 -0.1638811+1.430154i
#> 4 -0.6126444 1.688229 0.06 0.06 -0.6126444+1.688229i
#> 5 -1.0142687 1.963668 0.08 0.08 -1.0142687+1.963668i
#> 6 -1.4564235 2.206475 0.10 0.10 -1.4564235+2.206475i
#> 7 -1.9007785 2.451663 0.12 0.12 -1.9007785+2.451663i
#> 8 -2.3479978 2.704070 0.14 0.14 -2.3479978+2.704070i
#> 9 -2.8168798 2.975316 0.16 0.16 -2.8168798+2.975316i
#> 10 -3.2203012 3.194525 0.18 0.18 -3.2203012+3.194525i
#> 11 -3.6569867 3.419234 0.20 0.20 -3.6569867+3.419234i
#> 12 -4.1533065 3.628068 0.22 0.22 -4.1533065+3.628068i
#> 13 -4.6214190 3.769738 0.24 0.24 -4.6214190+3.769738i
#> 14 -5.0840916 3.917469 0.26 0.26 -5.0840916+3.917469i
#> 15 -5.6237349 4.029209 0.28 0.28 -5.6237349+4.029209i
#> 16 -6.1564404 4.153450 0.30 0.30 -6.1564404+4.153450i
#> 17 -6.7805035 4.383681 0.32 0.32 -6.7805035+4.383681i
#> 18 -7.3047805 4.543229 0.34 0.34 -7.3047805+4.543229i
#> 19 -7.8338499 4.729127 0.36 0.36 -7.8338499+4.729127i
#> 20 -8.2310982 4.874206 0.38 0.38 -8.2310982+4.874206i
#> 21 -8.7087997 5.022078 0.40 0.40 -8.7087997+5.022078i
#> 22 -9.1262530 5.187683 0.42 0.42 -9.1262530+5.187683i
#> 23 -9.6062128 5.372972 0.44 0.44 -9.6062128+5.372972i
#> 24 -10.1466988 5.558028 0.46 0.46 -10.1466988+5.558028i
#> 25 -10.6021477 5.727324 0.48 0.48 -10.6021477+5.727324i
#> 26 -11.1139695 5.914253 0.50 0.50 -11.1139695+5.914253i
#> 27 -11.6713247 6.187524 0.52 0.52 -11.6713247+6.187524i
#> 28 -12.1516172 6.410600 0.54 0.54 -12.1516172+6.410600i
#> 29 -12.6211101 6.598787 0.56 0.56 -12.6211101+6.598787i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_1 Sim_7 TrajSim_1_7
#> 2 -0.4723541+0.2591003i Traj_1 Sim_7 TrajSim_1_7
#> 3 -0.3875270+0.2250535i Traj_1 Sim_7 TrajSim_1_7
#> 4 -0.4487633+0.2580750i Traj_1 Sim_7 TrajSim_1_7
#> 5 -0.4016243+0.2754389i Traj_1 Sim_7 TrajSim_1_7
#> 6 -0.4421548+0.2428069i Traj_1 Sim_7 TrajSim_1_7
#> 7 -0.4443551+0.2451881i Traj_1 Sim_7 TrajSim_1_7
#> 8 -0.4472193+0.2524069i Traj_1 Sim_7 TrajSim_1_7
#> 9 -0.4688820+0.2712469i Traj_1 Sim_7 TrajSim_1_7
#> 10 -0.4034214+0.2192085i Traj_1 Sim_7 TrajSim_1_7
#> 11 -0.4366855+0.2247092i Traj_1 Sim_7 TrajSim_1_7
#> 12 -0.4963197+0.2088339i Traj_1 Sim_7 TrajSim_1_7
#> 13 -0.4681125+0.1416704i Traj_1 Sim_7 TrajSim_1_7
#> 14 -0.4626726+0.1477307i Traj_1 Sim_7 TrajSim_1_7
#> 15 -0.5396433+0.1117396i Traj_1 Sim_7 TrajSim_1_7
#> 16 -0.5327055+0.1242413i Traj_1 Sim_7 TrajSim_1_7
#> 17 -0.6240631+0.2302305i Traj_1 Sim_7 TrajSim_1_7
#> 18 -0.5242770+0.1595488i Traj_1 Sim_7 TrajSim_1_7
#> 19 -0.5290693+0.1858974i Traj_1 Sim_7 TrajSim_1_7
#> 20 -0.3972483+0.1450794i Traj_1 Sim_7 TrajSim_1_7
#> 21 -0.4777015+0.1478715i Traj_1 Sim_7 TrajSim_1_7
#> 22 -0.4174533+0.1656055i Traj_1 Sim_7 TrajSim_1_7
#> 23 -0.4799598+0.1852885i Traj_1 Sim_7 TrajSim_1_7
#> 24 -0.5404860+0.1850559i Traj_1 Sim_7 TrajSim_1_7
#> 25 -0.4554489+0.1692965i Traj_1 Sim_7 TrajSim_1_7
#> 26 -0.5118218+0.1869287i Traj_1 Sim_7 TrajSim_1_7
#> 27 -0.5573553+0.2732717i Traj_1 Sim_7 TrajSim_1_7
#> 28 -0.4802924+0.2230751i Traj_1 Sim_7 TrajSim_1_7
#> 29 -0.4694929+0.1881878i Traj_1 Sim_7 TrajSim_1_7
#>
#> [[7]][[2]]
#> x y time displacementTime polar
#> 1 0.33600000 1.560000 0.00 0.00 0.33600000+ 1.560000i
#> 2 0.02801463 2.065071 0.02 0.02 0.02801463+ 2.065071i
#> 3 -0.28873137 2.606055 0.04 0.04 -0.28873137+ 2.606055i
#> 4 -0.56466338 3.118874 0.06 0.06 -0.56466338+ 3.118874i
#> 5 -0.80460609 3.518160 0.08 0.08 -0.80460609+ 3.518160i
#> 6 -1.13729574 3.979333 0.10 0.10 -1.13729574+ 3.979333i
#> 7 -1.43962556 4.426696 0.12 0.12 -1.43962556+ 4.426696i
#> 8 -1.72590859 4.971836 0.14 0.14 -1.72590859+ 4.971836i
#> 9 -1.99528988 5.453073 0.16 0.16 -1.99528988+ 5.453073i
#> 10 -2.43122159 5.880805 0.18 0.18 -2.43122159+ 5.880805i
#> 11 -3.05777183 6.276969 0.20 0.20 -3.05777183+ 6.276969i
#> 12 -3.61033176 6.813036 0.22 0.22 -3.61033176+ 6.813036i
#> 13 -3.97610837 7.229402 0.24 0.24 -3.97610837+ 7.229402i
#> 14 -4.31975246 7.669700 0.26 0.26 -4.31975246+ 7.669700i
#> 15 -4.69774174 8.107752 0.28 0.28 -4.69774174+ 8.107752i
#> 16 -5.10910936 8.441255 0.30 0.30 -5.10910936+ 8.441255i
#> 17 -5.65653324 8.867651 0.32 0.32 -5.65653324+ 8.867651i
#> 18 -6.26255903 9.285459 0.34 0.34 -6.26255903+ 9.285459i
#> 19 -6.62962185 9.541626 0.36 0.36 -6.62962185+ 9.541626i
#> 20 -7.17309466 9.803061 0.38 0.38 -7.17309466+ 9.803061i
#> 21 -7.79619642 10.183537 0.40 0.40 -7.79619642+10.183537i
#> 22 -8.28695921 10.522635 0.42 0.42 -8.28695921+10.522635i
#> 23 -8.66724731 11.017161 0.44 0.44 -8.66724731+11.017161i
#> 24 -9.17488196 11.464662 0.46 0.46 -9.17488196+11.464662i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_2 Sim_7 TrajSim_2_7
#> 2 -0.3079854+0.5050711i Traj_2 Sim_7 TrajSim_2_7
#> 3 -0.3167460+0.5409836i Traj_2 Sim_7 TrajSim_2_7
#> 4 -0.2759320+0.5128194i Traj_2 Sim_7 TrajSim_2_7
#> 5 -0.2399427+0.3992862i Traj_2 Sim_7 TrajSim_2_7
#> 6 -0.3326897+0.4611729i Traj_2 Sim_7 TrajSim_2_7
#> 7 -0.3023298+0.4473628i Traj_2 Sim_7 TrajSim_2_7
#> 8 -0.2862830+0.5451403i Traj_2 Sim_7 TrajSim_2_7
#> 9 -0.2693813+0.4812365i Traj_2 Sim_7 TrajSim_2_7
#> 10 -0.4359317+0.4277326i Traj_2 Sim_7 TrajSim_2_7
#> 11 -0.6265502+0.3961639i Traj_2 Sim_7 TrajSim_2_7
#> 12 -0.5525599+0.5360668i Traj_2 Sim_7 TrajSim_2_7
#> 13 -0.3657766+0.4163662i Traj_2 Sim_7 TrajSim_2_7
#> 14 -0.3436441+0.4402973i Traj_2 Sim_7 TrajSim_2_7
#> 15 -0.3779893+0.4380520i Traj_2 Sim_7 TrajSim_2_7
#> 16 -0.4113676+0.3335036i Traj_2 Sim_7 TrajSim_2_7
#> 17 -0.5474239+0.4263963i Traj_2 Sim_7 TrajSim_2_7
#> 18 -0.6060258+0.4178076i Traj_2 Sim_7 TrajSim_2_7
#> 19 -0.3670628+0.2561668i Traj_2 Sim_7 TrajSim_2_7
#> 20 -0.5434728+0.2614350i Traj_2 Sim_7 TrajSim_2_7
#> 21 -0.6231018+0.3804764i Traj_2 Sim_7 TrajSim_2_7
#> 22 -0.4907628+0.3390981i Traj_2 Sim_7 TrajSim_2_7
#> 23 -0.3802881+0.4945260i Traj_2 Sim_7 TrajSim_2_7
#> 24 -0.5076346+0.4475003i Traj_2 Sim_7 TrajSim_2_7
#>
#>
#> [[8]]
#> [[8]][[1]]
#> x y time displacementTime polar
#> 1 0.69600000 0.946000 0.00 0.00 0.69600000+ 0.946000i
#> 2 0.52569419 1.470426 0.02 0.02 0.52569419+ 1.470426i
#> 3 0.34484959 1.991009 0.04 0.04 0.34484959+ 1.991009i
#> 4 0.19639665 2.479846 0.06 0.06 0.19639665+ 2.479846i
#> 5 0.06040769 3.085446 0.08 0.08 0.06040769+ 3.085446i
#> 6 -0.05080058 3.682067 0.10 0.10 -0.05080058+ 3.682067i
#> 7 -0.13083437 4.158337 0.12 0.12 -0.13083437+ 4.158337i
#> 8 -0.21727484 4.628365 0.14 0.14 -0.21727484+ 4.628365i
#> 9 -0.36584400 5.187998 0.16 0.16 -0.36584400+ 5.187998i
#> 10 -0.52960180 5.680046 0.18 0.18 -0.52960180+ 5.680046i
#> 11 -0.73788296 6.155689 0.20 0.20 -0.73788296+ 6.155689i
#> 12 -0.93691187 6.624848 0.22 0.22 -0.93691187+ 6.624848i
#> 13 -1.14968338 7.087946 0.24 0.24 -1.14968338+ 7.087946i
#> 14 -1.40353000 7.578807 0.26 0.26 -1.40353000+ 7.578807i
#> 15 -1.65663888 8.037624 0.28 0.28 -1.65663888+ 8.037624i
#> 16 -1.87446907 8.518500 0.30 0.30 -1.87446907+ 8.518500i
#> 17 -2.08304698 8.950965 0.32 0.32 -2.08304698+ 8.950965i
#> 18 -2.29795281 9.331095 0.34 0.34 -2.29795281+ 9.331095i
#> 19 -2.55633662 9.754569 0.36 0.36 -2.55633662+ 9.754569i
#> 20 -2.79367877 10.163472 0.38 0.38 -2.79367877+10.163472i
#> 21 -3.04966817 10.622101 0.40 0.40 -3.04966817+10.622101i
#> 22 -3.27672298 11.115749 0.42 0.42 -3.27672298+11.115749i
#> 23 -3.54676434 11.560027 0.44 0.44 -3.54676434+11.560027i
#> 24 -3.86087094 12.068958 0.46 0.46 -3.86087094+12.068958i
#> 25 -4.14204806 12.496186 0.48 0.48 -4.14204806+12.496186i
#> 26 -4.47360401 13.018532 0.50 0.50 -4.47360401+13.018532i
#> 27 -4.82516632 13.508118 0.52 0.52 -4.82516632+13.508118i
#> 28 -5.18408108 13.939440 0.54 0.54 -5.18408108+13.939440i
#> 29 -5.50899860 14.292845 0.56 0.56 -5.50899860+14.292845i
#> displacement Trajectory Simulation TrajSim
#> 1 0.00000000+0.0000000i Traj_1 Sim_8 TrajSim_1_8
#> 2 -0.17030581+0.5244262i Traj_1 Sim_8 TrajSim_1_8
#> 3 -0.18084461+0.5205825i Traj_1 Sim_8 TrajSim_1_8
#> 4 -0.14845294+0.4888375i Traj_1 Sim_8 TrajSim_1_8
#> 5 -0.13598896+0.6055996i Traj_1 Sim_8 TrajSim_1_8
#> 6 -0.11120827+0.5966208i Traj_1 Sim_8 TrajSim_1_8
#> 7 -0.08003380+0.4762700i Traj_1 Sim_8 TrajSim_1_8
#> 8 -0.08644046+0.4700283i Traj_1 Sim_8 TrajSim_1_8
#> 9 -0.14856916+0.5596330i Traj_1 Sim_8 TrajSim_1_8
#> 10 -0.16375780+0.4920482i Traj_1 Sim_8 TrajSim_1_8
#> 11 -0.20828116+0.4756424i Traj_1 Sim_8 TrajSim_1_8
#> 12 -0.19902891+0.4691591i Traj_1 Sim_8 TrajSim_1_8
#> 13 -0.21277151+0.4630988i Traj_1 Sim_8 TrajSim_1_8
#> 14 -0.25384662+0.4908603i Traj_1 Sim_8 TrajSim_1_8
#> 15 -0.25310888+0.4588176i Traj_1 Sim_8 TrajSim_1_8
#> 16 -0.21783019+0.4808755i Traj_1 Sim_8 TrajSim_1_8
#> 17 -0.20857791+0.4324650i Traj_1 Sim_8 TrajSim_1_8
#> 18 -0.21490584+0.3801296i Traj_1 Sim_8 TrajSim_1_8
#> 19 -0.25838381+0.4234739i Traj_1 Sim_8 TrajSim_1_8
#> 20 -0.23734215+0.4089030i Traj_1 Sim_8 TrajSim_1_8
#> 21 -0.25598940+0.4586292i Traj_1 Sim_8 TrajSim_1_8
#> 22 -0.22705481+0.4936487i Traj_1 Sim_8 TrajSim_1_8
#> 23 -0.27004137+0.4442776i Traj_1 Sim_8 TrajSim_1_8
#> 24 -0.31410660+0.5089305i Traj_1 Sim_8 TrajSim_1_8
#> 25 -0.28117711+0.4272284i Traj_1 Sim_8 TrajSim_1_8
#> 26 -0.33155595+0.5223464i Traj_1 Sim_8 TrajSim_1_8
#> 27 -0.35156231+0.4895857i Traj_1 Sim_8 TrajSim_1_8
#> 28 -0.35891475+0.4313217i Traj_1 Sim_8 TrajSim_1_8
#> 29 -0.32491753+0.3534054i Traj_1 Sim_8 TrajSim_1_8
#>
#> [[8]][[2]]
#> x y time displacementTime polar
#> 1 0.3360000 1.560000 0.00 0.00 0.3360000+1.560000i
#> 2 0.7391641 1.906746 0.02 0.02 0.7391641+1.906746i
#> 3 1.2790472 2.177680 0.04 0.04 1.2790472+2.177680i
#> 4 1.8409414 2.385779 0.06 0.06 1.8409414+2.385779i
#> 5 2.2694808 2.551921 0.08 0.08 2.2694808+2.551921i
#> 6 2.8366498 2.726351 0.10 0.10 2.8366498+2.726351i
#> 7 3.3582693 2.872566 0.12 0.12 3.3582693+2.872566i
#> 8 4.0465514 3.115390 0.14 0.14 4.0465514+3.115390i
#> 9 4.6711442 3.230914 0.16 0.16 4.6711442+3.230914i
#> 10 5.3680227 3.347289 0.18 0.18 5.3680227+3.347289i
#> 11 6.0182663 3.446561 0.20 0.20 6.0182663+3.446561i
#> 12 6.5201497 3.482180 0.22 0.22 6.5201497+3.482180i
#> 13 7.0613911 3.510986 0.24 0.24 7.0613911+3.510986i
#> 14 7.4673885 3.526732 0.26 0.26 7.4673885+3.526732i
#> 15 8.0527490 3.622839 0.28 0.28 8.0527490+3.622839i
#> 16 8.8345233 3.686941 0.30 0.30 8.8345233+3.686941i
#> 17 9.5379999 3.645822 0.32 0.32 9.5379999+3.645822i
#> 18 10.2747401 3.599076 0.34 0.34 10.2747401+3.599076i
#> 19 10.8568836 3.447286 0.36 0.36 10.8568836+3.447286i
#> 20 11.4289084 3.268077 0.38 0.38 11.4289084+3.268077i
#> 21 11.9496070 3.059522 0.40 0.40 11.9496070+3.059522i
#> 22 12.5259748 2.744810 0.42 0.42 12.5259748+2.744810i
#> 23 13.1395805 2.484858 0.44 0.44 13.1395805+2.484858i
#> 24 13.7585350 2.310752 0.46 0.46 13.7585350+2.310752i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.00000000i Traj_2 Sim_8 TrajSim_2_8
#> 2 0.4031641+0.34674568i Traj_2 Sim_8 TrajSim_2_8
#> 3 0.5398832+0.27093449i Traj_2 Sim_8 TrajSim_2_8
#> 4 0.5618941+0.20809856i Traj_2 Sim_8 TrajSim_2_8
#> 5 0.4285394+0.16614207i Traj_2 Sim_8 TrajSim_2_8
#> 6 0.5671690+0.17443036i Traj_2 Sim_8 TrajSim_2_8
#> 7 0.5216195+0.14621440i Traj_2 Sim_8 TrajSim_2_8
#> 8 0.6882822+0.24282423i Traj_2 Sim_8 TrajSim_2_8
#> 9 0.6245927+0.11552417i Traj_2 Sim_8 TrajSim_2_8
#> 10 0.6968785+0.11637549i Traj_2 Sim_8 TrajSim_2_8
#> 11 0.6502436+0.09927129i Traj_2 Sim_8 TrajSim_2_8
#> 12 0.5018834+0.03561916i Traj_2 Sim_8 TrajSim_2_8
#> 13 0.5412414+0.02880652i Traj_2 Sim_8 TrajSim_2_8
#> 14 0.4059974+0.01574597i Traj_2 Sim_8 TrajSim_2_8
#> 15 0.5853605+0.09610648i Traj_2 Sim_8 TrajSim_2_8
#> 16 0.7817744+0.06410177i Traj_2 Sim_8 TrajSim_2_8
#> 17 0.7034766-0.04111868i Traj_2 Sim_8 TrajSim_2_8
#> 18 0.7367402-0.04674575i Traj_2 Sim_8 TrajSim_2_8
#> 19 0.5821435-0.15179051i Traj_2 Sim_8 TrajSim_2_8
#> 20 0.5720248-0.17920854i Traj_2 Sim_8 TrajSim_2_8
#> 21 0.5206985-0.20855532i Traj_2 Sim_8 TrajSim_2_8
#> 22 0.5763678-0.31471182i Traj_2 Sim_8 TrajSim_2_8
#> 23 0.6136057-0.25995223i Traj_2 Sim_8 TrajSim_2_8
#> 24 0.6189545-0.17410608i Traj_2 Sim_8 TrajSim_2_8
#>
#>
#> [[9]]
#> [[9]][[1]]
#> x y time displacementTime polar
#> 1 0.6960000 0.9460000 0.00 0.00 0.6960000+ 0.9460000i
#> 2 0.8686711 0.3640813 0.02 0.02 0.8686711+ 0.3640813i
#> 3 1.0190334 -0.1977070 0.04 0.04 1.0190334- 0.1977070i
#> 4 1.1239464 -0.6959377 0.06 0.06 1.1239464- 0.6959377i
#> 5 1.1906178 -1.1723627 0.08 0.08 1.1906178- 1.1723627i
#> 6 1.2245340 -1.6773450 0.10 0.10 1.2245340- 1.6773450i
#> 7 1.2368974 -2.2712962 0.12 0.12 1.2368974- 2.2712962i
#> 8 1.2532724 -2.7740004 0.14 0.14 1.2532724- 2.7740004i
#> 9 1.3111061 -3.3294005 0.16 0.16 1.3111061- 3.3294005i
#> 10 1.3736565 -3.8477572 0.18 0.18 1.3736565- 3.8477572i
#> 11 1.4153795 -4.3441166 0.20 0.20 1.4153795- 4.3441166i
#> 12 1.4453845 -4.8261943 0.22 0.22 1.4453845- 4.8261943i
#> 13 1.4424298 -5.4343707 0.24 0.24 1.4424298- 5.4343707i
#> 14 1.4308832 -5.8627324 0.26 0.26 1.4308832- 5.8627324i
#> 15 1.4050753 -6.4485891 0.28 0.28 1.4050753- 6.4485891i
#> 16 1.3774623 -7.0457532 0.30 0.30 1.3774623- 7.0457532i
#> 17 1.3510720 -7.6285953 0.32 0.32 1.3510720- 7.6285953i
#> 18 1.3620264 -8.2060481 0.34 0.34 1.3620264- 8.2060481i
#> 19 1.3849494 -8.7197768 0.36 0.36 1.3849494- 8.7197768i
#> 20 1.4303429 -9.2721140 0.38 0.38 1.4303429- 9.2721140i
#> 21 1.4187321 -9.7738005 0.40 0.40 1.4187321- 9.7738005i
#> 22 1.3548714 -10.3286841 0.42 0.42 1.3548714-10.3286841i
#> 23 1.2685791 -10.8266851 0.44 0.44 1.2685791-10.8266851i
#> 24 1.1661459 -11.3647744 0.46 0.46 1.1661459-11.3647744i
#> 25 1.0967126 -11.8359298 0.48 0.48 1.0967126-11.8359298i
#> 26 1.1013292 -12.3770064 0.50 0.50 1.1013292-12.3770064i
#> 27 1.1303670 -12.9344806 0.52 0.52 1.1303670-12.9344806i
#> 28 1.1752631 -13.4897141 0.54 0.54 1.1752631-13.4897141i
#> 29 1.2304488 -13.9979037 0.56 0.56 1.2304488-13.9979037i
#> displacement Trajectory Simulation TrajSim
#> 1 0.000000000+0.0000000i Traj_1 Sim_9 TrajSim_1_9
#> 2 0.172671075-0.5819187i Traj_1 Sim_9 TrajSim_1_9
#> 3 0.150362292-0.5617883i Traj_1 Sim_9 TrajSim_1_9
#> 4 0.104913014-0.4982307i Traj_1 Sim_9 TrajSim_1_9
#> 5 0.066671420-0.4764250i Traj_1 Sim_9 TrajSim_1_9
#> 6 0.033916199-0.5049823i Traj_1 Sim_9 TrajSim_1_9
#> 7 0.012363409-0.5939511i Traj_1 Sim_9 TrajSim_1_9
#> 8 0.016375036-0.5027043i Traj_1 Sim_9 TrajSim_1_9
#> 9 0.057833661-0.5554000i Traj_1 Sim_9 TrajSim_1_9
#> 10 0.062550399-0.5183567i Traj_1 Sim_9 TrajSim_1_9
#> 11 0.041723001-0.4963593i Traj_1 Sim_9 TrajSim_1_9
#> 12 0.030004987-0.4820778i Traj_1 Sim_9 TrajSim_1_9
#> 13 -0.002954721-0.6081764i Traj_1 Sim_9 TrajSim_1_9
#> 14 -0.011546617-0.4283617i Traj_1 Sim_9 TrajSim_1_9
#> 15 -0.025807820-0.5858566i Traj_1 Sim_9 TrajSim_1_9
#> 16 -0.027613064-0.5971641i Traj_1 Sim_9 TrajSim_1_9
#> 17 -0.026390288-0.5828421i Traj_1 Sim_9 TrajSim_1_9
#> 18 0.010954401-0.5774528i Traj_1 Sim_9 TrajSim_1_9
#> 19 0.022923030-0.5137287i Traj_1 Sim_9 TrajSim_1_9
#> 20 0.045393457-0.5523372i Traj_1 Sim_9 TrajSim_1_9
#> 21 -0.011610755-0.5016864i Traj_1 Sim_9 TrajSim_1_9
#> 22 -0.063860677-0.5548836i Traj_1 Sim_9 TrajSim_1_9
#> 23 -0.086292341-0.4980010i Traj_1 Sim_9 TrajSim_1_9
#> 24 -0.102433228-0.5380893i Traj_1 Sim_9 TrajSim_1_9
#> 25 -0.069433253-0.4711554i Traj_1 Sim_9 TrajSim_1_9
#> 26 0.004616621-0.5410766i Traj_1 Sim_9 TrajSim_1_9
#> 27 0.029037738-0.5574742i Traj_1 Sim_9 TrajSim_1_9
#> 28 0.044896111-0.5552335i Traj_1 Sim_9 TrajSim_1_9
#> 29 0.055185702-0.5081896i Traj_1 Sim_9 TrajSim_1_9
#>
#> [[9]][[2]]
#> x y time displacementTime polar
#> 1 0.33600000 1.560000 0.00 0.00 0.33600000+ 1.560000i
#> 2 0.11714438 2.165201 0.02 0.02 0.11714438+ 2.165201i
#> 3 -0.01523418 2.698141 0.04 0.04 -0.01523418+ 2.698141i
#> 4 -0.18248433 3.388258 0.06 0.06 -0.18248433+ 3.388258i
#> 5 -0.34802086 4.004353 0.08 0.08 -0.34802086+ 4.004353i
#> 6 -0.27969375 4.564783 0.10 0.10 -0.27969375+ 4.564783i
#> 7 -0.09436583 5.143122 0.12 0.12 -0.09436583+ 5.143122i
#> 8 0.09794411 5.598186 0.14 0.14 0.09794411+ 5.598186i
#> 9 0.37712957 6.224288 0.16 0.16 0.37712957+ 6.224288i
#> 10 0.50011823 6.757257 0.18 0.18 0.50011823+ 6.757257i
#> 11 0.71014935 7.342437 0.20 0.20 0.71014935+ 7.342437i
#> 12 0.90936519 8.005853 0.22 0.22 0.90936519+ 8.005853i
#> 13 1.12317592 8.523592 0.24 0.24 1.12317592+ 8.523592i
#> 14 1.34295404 9.020027 0.26 0.26 1.34295404+ 9.020027i
#> 15 1.60485282 9.635385 0.28 0.28 1.60485282+ 9.635385i
#> 16 1.70600296 10.203272 0.30 0.30 1.70600296+10.203272i
#> 17 1.84151042 10.799317 0.32 0.32 1.84151042+10.799317i
#> 18 2.04247705 11.326482 0.34 0.34 2.04247705+11.326482i
#> 19 2.25789779 11.807663 0.36 0.36 2.25789779+11.807663i
#> 20 2.58207625 12.491353 0.38 0.38 2.58207625+12.491353i
#> 21 2.80325870 12.955438 0.40 0.40 2.80325870+12.955438i
#> 22 3.02196436 13.341959 0.42 0.42 3.02196436+13.341959i
#> 23 3.31760626 13.916644 0.44 0.44 3.31760626+13.916644i
#> 24 3.63083156 14.564325 0.46 0.46 3.63083156+14.564325i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_2 Sim_9 TrajSim_2_9
#> 2 -0.2188556+0.6052008i Traj_2 Sim_9 TrajSim_2_9
#> 3 -0.1323786+0.5329398i Traj_2 Sim_9 TrajSim_2_9
#> 4 -0.1672502+0.6901170i Traj_2 Sim_9 TrajSim_2_9
#> 5 -0.1655365+0.6160953i Traj_2 Sim_9 TrajSim_2_9
#> 6 0.0683271+0.5604303i Traj_2 Sim_9 TrajSim_2_9
#> 7 0.1853279+0.5783389i Traj_2 Sim_9 TrajSim_2_9
#> 8 0.1923099+0.4550644i Traj_2 Sim_9 TrajSim_2_9
#> 9 0.2791855+0.6261020i Traj_2 Sim_9 TrajSim_2_9
#> 10 0.1229887+0.5329683i Traj_2 Sim_9 TrajSim_2_9
#> 11 0.2100311+0.5851798i Traj_2 Sim_9 TrajSim_2_9
#> 12 0.1992158+0.6634166i Traj_2 Sim_9 TrajSim_2_9
#> 13 0.2138107+0.5177388i Traj_2 Sim_9 TrajSim_2_9
#> 14 0.2197781+0.4964347i Traj_2 Sim_9 TrajSim_2_9
#> 15 0.2618988+0.6153582i Traj_2 Sim_9 TrajSim_2_9
#> 16 0.1011501+0.5678869i Traj_2 Sim_9 TrajSim_2_9
#> 17 0.1355075+0.5960452i Traj_2 Sim_9 TrajSim_2_9
#> 18 0.2009666+0.5271647i Traj_2 Sim_9 TrajSim_2_9
#> 19 0.2154207+0.4811811i Traj_2 Sim_9 TrajSim_2_9
#> 20 0.3241785+0.6836903i Traj_2 Sim_9 TrajSim_2_9
#> 21 0.2211825+0.4640853i Traj_2 Sim_9 TrajSim_2_9
#> 22 0.2187057+0.3865211i Traj_2 Sim_9 TrajSim_2_9
#> 23 0.2956419+0.5746849i Traj_2 Sim_9 TrajSim_2_9
#> 24 0.3132253+0.6476808i Traj_2 Sim_9 TrajSim_2_9
#>
#>
#> [[10]]
#> [[10]][[1]]
#> x y time displacementTime polar
#> 1 0.696000 0.9460000 0.00 0.00 0.696000+0.9460000i
#> 2 1.239602 0.7049379 0.02 0.02 1.239602+0.7049379i
#> 3 1.717724 0.4633800 0.04 0.04 1.717724+0.4633800i
#> 4 2.197382 0.1700410 0.06 0.06 2.197382+0.1700410i
#> 5 2.641728 -0.0711128 0.08 0.08 2.641728-0.0711128i
#> 6 3.083733 -0.2861560 0.10 0.10 3.083733-0.2861560i
#> 7 3.608736 -0.5505553 0.12 0.12 3.608736-0.5505553i
#> 8 4.091467 -0.7923734 0.14 0.14 4.091467-0.7923734i
#> 9 4.615110 -1.0959168 0.16 0.16 4.615110-1.0959168i
#> 10 5.062733 -1.3761674 0.18 0.18 5.062733-1.3761674i
#> 11 5.545885 -1.6590124 0.20 0.20 5.545885-1.6590124i
#> 12 6.017702 -1.9756761 0.22 0.22 6.017702-1.9756761i
#> 13 6.447664 -2.2355003 0.24 0.24 6.447664-2.2355003i
#> 14 6.993233 -2.5250473 0.26 0.26 6.993233-2.5250473i
#> 15 7.475484 -2.7425184 0.28 0.28 7.475484-2.7425184i
#> 16 8.051921 -2.9826375 0.30 0.30 8.051921-2.9826375i
#> 17 8.496805 -3.1919324 0.32 0.32 8.496805-3.1919324i
#> 18 8.989471 -3.3995408 0.34 0.34 8.989471-3.3995408i
#> 19 9.553123 -3.5509523 0.36 0.36 9.553123-3.5509523i
#> 20 10.121817 -3.6699291 0.38 0.38 10.121817-3.6699291i
#> 21 10.787044 -3.7499023 0.40 0.40 10.787044-3.7499023i
#> 22 11.288743 -3.8247384 0.42 0.42 11.288743-3.8247384i
#> 23 11.892389 -3.9988395 0.44 0.44 11.892389-3.9988395i
#> 24 12.405842 -4.1296685 0.46 0.46 12.405842-4.1296685i
#> 25 12.863843 -4.2327342 0.48 0.48 12.863843-4.2327342i
#> 26 13.480790 -4.3531193 0.50 0.50 13.480790-4.3531193i
#> 27 14.093178 -4.4393909 0.52 0.52 14.093178-4.4393909i
#> 28 14.639346 -4.5461696 0.54 0.54 14.639346-4.5461696i
#> 29 15.216857 -4.6245525 0.56 0.56 15.216857-4.6245525i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.00000000i Traj_1 Sim_10 TrajSim_1_10
#> 2 0.5436016-0.24106209i Traj_1 Sim_10 TrajSim_1_10
#> 3 0.4781221-0.24155788i Traj_1 Sim_10 TrajSim_1_10
#> 4 0.4796587-0.29333899i Traj_1 Sim_10 TrajSim_1_10
#> 5 0.4443457-0.24115384i Traj_1 Sim_10 TrajSim_1_10
#> 6 0.4420049-0.21504318i Traj_1 Sim_10 TrajSim_1_10
#> 7 0.5250032-0.26439933i Traj_1 Sim_10 TrajSim_1_10
#> 8 0.4827310-0.24181812i Traj_1 Sim_10 TrajSim_1_10
#> 9 0.5236426-0.30354335i Traj_1 Sim_10 TrajSim_1_10
#> 10 0.4476228-0.28025063i Traj_1 Sim_10 TrajSim_1_10
#> 11 0.4831520-0.28284493i Traj_1 Sim_10 TrajSim_1_10
#> 12 0.4718171-0.31666374i Traj_1 Sim_10 TrajSim_1_10
#> 13 0.4299618-0.25982420i Traj_1 Sim_10 TrajSim_1_10
#> 14 0.5455690-0.28954699i Traj_1 Sim_10 TrajSim_1_10
#> 15 0.4822518-0.21747107i Traj_1 Sim_10 TrajSim_1_10
#> 16 0.5764364-0.24011914i Traj_1 Sim_10 TrajSim_1_10
#> 17 0.4448846-0.20929494i Traj_1 Sim_10 TrajSim_1_10
#> 18 0.4926658-0.20760839i Traj_1 Sim_10 TrajSim_1_10
#> 19 0.5636520-0.15141146i Traj_1 Sim_10 TrajSim_1_10
#> 20 0.5686941-0.11897683i Traj_1 Sim_10 TrajSim_1_10
#> 21 0.6652272-0.07997316i Traj_1 Sim_10 TrajSim_1_10
#> 22 0.5016988-0.07483612i Traj_1 Sim_10 TrajSim_1_10
#> 23 0.6036461-0.17410111i Traj_1 Sim_10 TrajSim_1_10
#> 24 0.5134527-0.13082902i Traj_1 Sim_10 TrajSim_1_10
#> 25 0.4580012-0.10306572i Traj_1 Sim_10 TrajSim_1_10
#> 26 0.6169470-0.12038503i Traj_1 Sim_10 TrajSim_1_10
#> 27 0.6123875-0.08627164i Traj_1 Sim_10 TrajSim_1_10
#> 28 0.5461687-0.10677875i Traj_1 Sim_10 TrajSim_1_10
#> 29 0.5775108-0.07838281i Traj_1 Sim_10 TrajSim_1_10
#>
#> [[10]][[2]]
#> x y time displacementTime polar
#> 1 0.33600000 1.5600000 0.00 0.00 0.33600000+ 1.5600000i
#> 2 0.19710498 1.0196224 0.02 0.02 0.19710498+ 1.0196224i
#> 3 0.10011715 0.4583109 0.04 0.04 0.10011715+ 0.4583109i
#> 4 0.05435489 -0.1139063 0.06 0.06 0.05435489- 0.1139063i
#> 5 0.01008930 -0.5737248 0.08 0.08 0.01008930- 0.5737248i
#> 6 -0.06715739 -0.9920086 0.10 0.10 -0.06715739- 0.9920086i
#> 7 -0.08962469 -1.7672070 0.12 0.12 -0.08962469- 1.7672070i
#> 8 -0.05910459 -2.2895638 0.14 0.14 -0.05910459- 2.2895638i
#> 9 -0.10584900 -3.0247009 0.16 0.16 -0.10584900- 3.0247009i
#> 10 -0.19934405 -3.5539045 0.18 0.18 -0.19934405- 3.5539045i
#> 11 -0.23171763 -4.2121965 0.20 0.20 -0.23171763- 4.2121965i
#> 12 -0.23276963 -4.7695025 0.22 0.22 -0.23276963- 4.7695025i
#> 13 -0.02937459 -5.5058235 0.24 0.24 -0.02937459- 5.5058235i
#> 14 0.15397406 -6.0286645 0.26 0.26 0.15397406- 6.0286645i
#> 15 0.35461809 -6.6906075 0.28 0.28 0.35461809- 6.6906075i
#> 16 0.55600000 -7.3777440 0.30 0.30 0.55600000- 7.3777440i
#> 17 0.90049188 -8.0192214 0.32 0.32 0.90049188- 8.0192214i
#> 18 1.07643879 -8.4711957 0.34 0.34 1.07643879- 8.4711957i
#> 19 1.22349818 -9.0770467 0.36 0.36 1.22349818- 9.0770467i
#> 20 1.36900727 -9.7028807 0.38 0.38 1.36900727- 9.7028807i
#> 21 1.61638792 -10.3223581 0.40 0.40 1.61638792-10.3223581i
#> 22 1.72823954 -10.7973399 0.42 0.42 1.72823954-10.7973399i
#> 23 1.83394301 -11.4510348 0.44 0.44 1.83394301-11.4510348i
#> 24 1.94467108 -12.0801153 0.46 0.46 1.94467108-12.0801153i
#> displacement Trajectory Simulation TrajSim
#> 1 0.00000000+0.0000000i Traj_2 Sim_10 TrajSim_2_10
#> 2 -0.13889502-0.5403776i Traj_2 Sim_10 TrajSim_2_10
#> 3 -0.09698783-0.5613115i Traj_2 Sim_10 TrajSim_2_10
#> 4 -0.04576226-0.5722172i Traj_2 Sim_10 TrajSim_2_10
#> 5 -0.04426560-0.4598185i Traj_2 Sim_10 TrajSim_2_10
#> 6 -0.07724669-0.4182838i Traj_2 Sim_10 TrajSim_2_10
#> 7 -0.02246730-0.7751984i Traj_2 Sim_10 TrajSim_2_10
#> 8 0.03052011-0.5223569i Traj_2 Sim_10 TrajSim_2_10
#> 9 -0.04674441-0.7351371i Traj_2 Sim_10 TrajSim_2_10
#> 10 -0.09349505-0.5292035i Traj_2 Sim_10 TrajSim_2_10
#> 11 -0.03237359-0.6582920i Traj_2 Sim_10 TrajSim_2_10
#> 12 -0.00105200-0.5573061i Traj_2 Sim_10 TrajSim_2_10
#> 13 0.20339505-0.7363209i Traj_2 Sim_10 TrajSim_2_10
#> 14 0.18334864-0.5228410i Traj_2 Sim_10 TrajSim_2_10
#> 15 0.20064404-0.6619431i Traj_2 Sim_10 TrajSim_2_10
#> 16 0.20138191-0.6871364i Traj_2 Sim_10 TrajSim_2_10
#> 17 0.34449188-0.6414774i Traj_2 Sim_10 TrajSim_2_10
#> 18 0.17594691-0.4519743i Traj_2 Sim_10 TrajSim_2_10
#> 19 0.14705939-0.6058509i Traj_2 Sim_10 TrajSim_2_10
#> 20 0.14550909-0.6258341i Traj_2 Sim_10 TrajSim_2_10
#> 21 0.24738065-0.6194774i Traj_2 Sim_10 TrajSim_2_10
#> 22 0.11185162-0.4749818i Traj_2 Sim_10 TrajSim_2_10
#> 23 0.10570347-0.6536949i Traj_2 Sim_10 TrajSim_2_10
#> 24 0.11072806-0.6290805i Traj_2 Sim_10 TrajSim_2_10
sim_directed_paluxy <- simulate_track(PaluxyRiver, nsim = 100, model = "Directed")
print(sim_directed_paluxy[1:10])#> [[1]]
#> [[1]][[1]]
#> x y time displacementTime polar
#> 1 0.6960000 0.946000 0.00 0.00 0.6960000+ 0.946000i
#> 2 0.7306096 1.533668 0.02 0.02 0.7306096+ 1.533668i
#> 3 0.7002691 2.079871 0.04 0.04 0.7002691+ 2.079871i
#> 4 0.6591542 2.657502 0.06 0.06 0.6591542+ 2.657502i
#> 5 0.7698013 3.254036 0.08 0.08 0.7698013+ 3.254036i
#> 6 0.8738125 3.837199 0.10 0.10 0.8738125+ 3.837199i
#> 7 0.9259900 4.447929 0.12 0.12 0.9259900+ 4.447929i
#> 8 0.9585292 4.917318 0.14 0.14 0.9585292+ 4.917318i
#> 9 0.9959397 5.419948 0.16 0.16 0.9959397+ 5.419948i
#> 10 0.9632891 6.019319 0.18 0.18 0.9632891+ 6.019319i
#> 11 1.0567016 6.434666 0.20 0.20 1.0567016+ 6.434666i
#> 12 1.1233596 6.935793 0.22 0.22 1.1233596+ 6.935793i
#> 13 1.1257901 7.398635 0.24 0.24 1.1257901+ 7.398635i
#> 14 1.1276306 7.910112 0.26 0.26 1.1276306+ 7.910112i
#> 15 1.1218653 8.396103 0.28 0.28 1.1218653+ 8.396103i
#> 16 1.1114880 8.920222 0.30 0.30 1.1114880+ 8.920222i
#> 17 1.0528410 9.453377 0.32 0.32 1.0528410+ 9.453377i
#> 18 0.9702158 9.887581 0.34 0.34 0.9702158+ 9.887581i
#> 19 0.9420555 10.395917 0.36 0.36 0.9420555+10.395917i
#> 20 1.0357933 10.955739 0.38 0.38 1.0357933+10.955739i
#> 21 1.2480077 11.514447 0.40 0.40 1.2480077+11.514447i
#> 22 1.0858706 12.092550 0.42 0.42 1.0858706+12.092550i
#> 23 1.0737296 12.508916 0.44 0.44 1.0737296+12.508916i
#> 24 1.0303953 13.021845 0.46 0.46 1.0303953+13.021845i
#> 25 1.0264168 13.594134 0.48 0.48 1.0264168+13.594134i
#> 26 0.9111610 14.060459 0.50 0.50 0.9111610+14.060459i
#> 27 0.9823530 14.537864 0.52 0.52 0.9823530+14.537864i
#> 28 1.0542507 15.105997 0.54 0.54 1.0542507+15.105997i
#> 29 0.9807594 15.590698 0.56 0.56 0.9807594+15.590698i
#> displacement Trajectory Simulation TrajSim
#> 1 0.000000000+0.0000000i Traj_1 Sim_1 TrajSim_1_1
#> 2 0.034609622+0.5876677i Traj_1 Sim_1 TrajSim_1_1
#> 3 -0.030340543+0.5462033i Traj_1 Sim_1 TrajSim_1_1
#> 4 -0.041114901+0.5776309i Traj_1 Sim_1 TrajSim_1_1
#> 5 0.110647103+0.5965338i Traj_1 Sim_1 TrajSim_1_1
#> 6 0.104011203+0.5831628i Traj_1 Sim_1 TrajSim_1_1
#> 7 0.052177468+0.6107305i Traj_1 Sim_1 TrajSim_1_1
#> 8 0.032539226+0.4693889i Traj_1 Sim_1 TrajSim_1_1
#> 9 0.037410566+0.5026300i Traj_1 Sim_1 TrajSim_1_1
#> 10 -0.032650609+0.5993713i Traj_1 Sim_1 TrajSim_1_1
#> 11 0.093412460+0.4153469i Traj_1 Sim_1 TrajSim_1_1
#> 12 0.066657982+0.5011272i Traj_1 Sim_1 TrajSim_1_1
#> 13 0.002430487+0.4628413i Traj_1 Sim_1 TrajSim_1_1
#> 14 0.001840523+0.5114771i Traj_1 Sim_1 TrajSim_1_1
#> 15 -0.005765252+0.4859916i Traj_1 Sim_1 TrajSim_1_1
#> 16 -0.010377330+0.5241184i Traj_1 Sim_1 TrajSim_1_1
#> 17 -0.058647007+0.5331549i Traj_1 Sim_1 TrajSim_1_1
#> 18 -0.082625239+0.4342045i Traj_1 Sim_1 TrajSim_1_1
#> 19 -0.028160278+0.5083358i Traj_1 Sim_1 TrajSim_1_1
#> 20 0.093737820+0.5598217i Traj_1 Sim_1 TrajSim_1_1
#> 21 0.212214349+0.5587081i Traj_1 Sim_1 TrajSim_1_1
#> 22 -0.162137089+0.5781032i Traj_1 Sim_1 TrajSim_1_1
#> 23 -0.012140979+0.4163659i Traj_1 Sim_1 TrajSim_1_1
#> 24 -0.043334257+0.5129286i Traj_1 Sim_1 TrajSim_1_1
#> 25 -0.003978548+0.5722899i Traj_1 Sim_1 TrajSim_1_1
#> 26 -0.115255811+0.4663242i Traj_1 Sim_1 TrajSim_1_1
#> 27 0.071192058+0.4774054i Traj_1 Sim_1 TrajSim_1_1
#> 28 0.071897651+0.5681325i Traj_1 Sim_1 TrajSim_1_1
#> 29 -0.073491306+0.4847011i Traj_1 Sim_1 TrajSim_1_1
#>
#> [[1]][[2]]
#> x y time displacementTime polar
#> 1 0.3360000 1.560000 0.00 0.00 0.3360000+ 1.560000i
#> 2 0.4159697 2.178650 0.02 0.02 0.4159697+ 2.178650i
#> 3 0.6747166 2.816657 0.04 0.04 0.6747166+ 2.816657i
#> 4 0.7276437 3.248376 0.06 0.06 0.7276437+ 3.248376i
#> 5 0.7653507 3.828090 0.08 0.08 0.7653507+ 3.828090i
#> 6 0.8465195 4.489501 0.10 0.10 0.8465195+ 4.489501i
#> 7 0.8437310 5.033561 0.12 0.12 0.8437310+ 5.033561i
#> 8 0.8791833 5.696042 0.14 0.14 0.8791833+ 5.696042i
#> 9 0.8917716 6.257311 0.16 0.16 0.8917716+ 6.257311i
#> 10 0.9770601 6.863222 0.18 0.18 0.9770601+ 6.863222i
#> 11 1.1194308 7.500539 0.20 0.20 1.1194308+ 7.500539i
#> 12 1.1318824 8.134118 0.22 0.22 1.1318824+ 8.134118i
#> 13 1.1699135 8.673200 0.24 0.24 1.1699135+ 8.673200i
#> 14 1.2043428 9.228280 0.26 0.26 1.2043428+ 9.228280i
#> 15 1.3326141 9.884948 0.28 0.28 1.3326141+ 9.884948i
#> 16 1.3195584 10.572156 0.30 0.30 1.3195584+10.572156i
#> 17 1.5078971 11.271988 0.32 0.32 1.5078971+11.271988i
#> 18 1.5821391 11.814870 0.34 0.34 1.5821391+11.814870i
#> 19 1.6435431 12.369048 0.36 0.36 1.6435431+12.369048i
#> 20 1.7866207 12.804064 0.38 0.38 1.7866207+12.804064i
#> 21 1.8328871 13.373424 0.40 0.40 1.8328871+13.373424i
#> 22 1.8115303 13.850803 0.42 0.42 1.8115303+13.850803i
#> 23 1.9321137 14.464598 0.44 0.44 1.9321137+14.464598i
#> 24 2.0863649 15.183989 0.46 0.46 2.0863649+15.183989i
#> displacement Trajectory Simulation TrajSim
#> 1 0.000000000+0.0000000i Traj_2 Sim_1 TrajSim_2_1
#> 2 0.079969703+0.6186499i Traj_2 Sim_1 TrajSim_2_1
#> 3 0.258746932+0.6380072i Traj_2 Sim_1 TrajSim_2_1
#> 4 0.052927058+0.4317192i Traj_2 Sim_1 TrajSim_2_1
#> 5 0.037706975+0.5797136i Traj_2 Sim_1 TrajSim_2_1
#> 6 0.081168800+0.6614109i Traj_2 Sim_1 TrajSim_2_1
#> 7 -0.002788425+0.5440602i Traj_2 Sim_1 TrajSim_2_1
#> 8 0.035452232+0.6624807i Traj_2 Sim_1 TrajSim_2_1
#> 9 0.012588309+0.5612690i Traj_2 Sim_1 TrajSim_2_1
#> 10 0.085288547+0.6059118i Traj_2 Sim_1 TrajSim_2_1
#> 11 0.142370660+0.6373167i Traj_2 Sim_1 TrajSim_2_1
#> 12 0.012451567+0.6335791i Traj_2 Sim_1 TrajSim_2_1
#> 13 0.038031168+0.5390816i Traj_2 Sim_1 TrajSim_2_1
#> 14 0.034429263+0.5550801i Traj_2 Sim_1 TrajSim_2_1
#> 15 0.128271296+0.6566677i Traj_2 Sim_1 TrajSim_2_1
#> 16 -0.013055718+0.6872079i Traj_2 Sim_1 TrajSim_2_1
#> 17 0.188338756+0.6998318i Traj_2 Sim_1 TrajSim_2_1
#> 18 0.074241931+0.5428823i Traj_2 Sim_1 TrajSim_2_1
#> 19 0.061404001+0.5541781i Traj_2 Sim_1 TrajSim_2_1
#> 20 0.143077597+0.4350165i Traj_2 Sim_1 TrajSim_2_1
#> 21 0.046266400+0.5693600i Traj_2 Sim_1 TrajSim_2_1
#> 22 -0.021356789+0.4773788i Traj_2 Sim_1 TrajSim_2_1
#> 23 0.120583465+0.6137951i Traj_2 Sim_1 TrajSim_2_1
#> 24 0.154251173+0.7193903i Traj_2 Sim_1 TrajSim_2_1
#>
#>
#> [[2]]
#> [[2]][[1]]
#> x y time displacementTime polar
#> 1 0.6960000 0.946000 0.00 0.00 0.6960000+ 0.946000i
#> 2 0.6830977 1.383535 0.02 0.02 0.6830977+ 1.383535i
#> 3 0.8864011 1.971556 0.04 0.04 0.8864011+ 1.971556i
#> 4 0.9709203 2.480436 0.06 0.06 0.9709203+ 2.480436i
#> 5 0.8378025 3.141891 0.08 0.08 0.8378025+ 3.141891i
#> 6 0.8042141 3.720536 0.10 0.10 0.8042141+ 3.720536i
#> 7 0.8051742 4.247614 0.12 0.12 0.8051742+ 4.247614i
#> 8 0.9892427 4.757644 0.14 0.14 0.9892427+ 4.757644i
#> 9 1.0769503 5.257820 0.16 0.16 1.0769503+ 5.257820i
#> 10 1.0332977 5.671852 0.18 0.18 1.0332977+ 5.671852i
#> 11 1.0673469 6.117223 0.20 0.20 1.0673469+ 6.117223i
#> 12 1.0659312 6.654306 0.22 0.22 1.0659312+ 6.654306i
#> 13 1.1459346 7.162751 0.24 0.24 1.1459346+ 7.162751i
#> 14 1.1944624 7.759672 0.26 0.26 1.1944624+ 7.759672i
#> 15 1.1906956 8.245870 0.28 0.28 1.1906956+ 8.245870i
#> 16 1.3694624 8.762809 0.30 0.30 1.3694624+ 8.762809i
#> 17 1.4088562 9.280626 0.32 0.32 1.4088562+ 9.280626i
#> 18 1.5301208 9.829165 0.34 0.34 1.5301208+ 9.829165i
#> 19 1.6238208 10.425508 0.36 0.36 1.6238208+10.425508i
#> 20 1.5279673 11.021436 0.38 0.38 1.5279673+11.021436i
#> 21 1.5363128 11.569904 0.40 0.40 1.5363128+11.569904i
#> 22 1.6029594 12.065171 0.42 0.42 1.6029594+12.065171i
#> 23 1.5572235 12.635639 0.44 0.44 1.5572235+12.635639i
#> 24 1.5978426 13.154849 0.46 0.46 1.5978426+13.154849i
#> 25 1.4502355 13.800793 0.48 0.48 1.4502355+13.800793i
#> 26 1.5217958 14.337739 0.50 0.50 1.5217958+14.337739i
#> 27 1.7207065 14.820184 0.52 0.52 1.7207065+14.820184i
#> 28 1.7575005 15.280049 0.54 0.54 1.7575005+15.280049i
#> 29 1.7324011 15.894175 0.56 0.56 1.7324011+15.894175i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000000+0.0000000i Traj_1 Sim_2 TrajSim_1_2
#> 2 -0.0129022882+0.4375346i Traj_1 Sim_2 TrajSim_1_2
#> 3 0.2033033797+0.5880218i Traj_1 Sim_2 TrajSim_1_2
#> 4 0.0845191771+0.5088797i Traj_1 Sim_2 TrajSim_1_2
#> 5 -0.1331177931+0.6614550i Traj_1 Sim_2 TrajSim_1_2
#> 6 -0.0335883703+0.5786451i Traj_1 Sim_2 TrajSim_1_2
#> 7 0.0009600681+0.5270779i Traj_1 Sim_2 TrajSim_1_2
#> 8 0.1840685122+0.5100301i Traj_1 Sim_2 TrajSim_1_2
#> 9 0.0877076443+0.5001759i Traj_1 Sim_2 TrajSim_1_2
#> 10 -0.0436526763+0.4140315i Traj_1 Sim_2 TrajSim_1_2
#> 11 0.0340492528+0.4453714i Traj_1 Sim_2 TrajSim_1_2
#> 12 -0.0014157519+0.5370830i Traj_1 Sim_2 TrajSim_1_2
#> 13 0.0800034927+0.5084455i Traj_1 Sim_2 TrajSim_1_2
#> 14 0.0485277173+0.5969207i Traj_1 Sim_2 TrajSim_1_2
#> 15 -0.0037667542+0.4861976i Traj_1 Sim_2 TrajSim_1_2
#> 16 0.1787667473+0.5169391i Traj_1 Sim_2 TrajSim_1_2
#> 17 0.0393938253+0.5178175i Traj_1 Sim_2 TrajSim_1_2
#> 18 0.1212645824+0.5485384i Traj_1 Sim_2 TrajSim_1_2
#> 19 0.0936999882+0.5963428i Traj_1 Sim_2 TrajSim_1_2
#> 20 -0.0958534760+0.5959287i Traj_1 Sim_2 TrajSim_1_2
#> 21 0.0083455700+0.5484674i Traj_1 Sim_2 TrajSim_1_2
#> 22 0.0666465658+0.4952678i Traj_1 Sim_2 TrajSim_1_2
#> 23 -0.0457359125+0.5704677i Traj_1 Sim_2 TrajSim_1_2
#> 24 0.0406191011+0.5192100i Traj_1 Sim_2 TrajSim_1_2
#> 25 -0.1476071158+0.6459436i Traj_1 Sim_2 TrajSim_1_2
#> 26 0.0715603423+0.5369459i Traj_1 Sim_2 TrajSim_1_2
#> 27 0.1989106399+0.4824457i Traj_1 Sim_2 TrajSim_1_2
#> 28 0.0367939948+0.4598646i Traj_1 Sim_2 TrajSim_1_2
#> 29 -0.0250993982+0.6141264i Traj_1 Sim_2 TrajSim_1_2
#>
#> [[2]][[2]]
#> x y time displacementTime polar
#> 1 0.3360000 1.560000 0.00 0.00 0.3360000+ 1.560000i
#> 2 0.3563407 2.259740 0.02 0.02 0.3563407+ 2.259740i
#> 3 0.4625914 2.877217 0.04 0.04 0.4625914+ 2.877217i
#> 4 0.6466001 3.441230 0.06 0.06 0.6466001+ 3.441230i
#> 5 0.6829347 4.196902 0.08 0.08 0.6829347+ 4.196902i
#> 6 0.6955396 4.731184 0.10 0.10 0.6955396+ 4.731184i
#> 7 0.8508694 5.307454 0.12 0.12 0.8508694+ 5.307454i
#> 8 0.9129618 5.929082 0.14 0.14 0.9129618+ 5.929082i
#> 9 0.9214394 6.599344 0.16 0.16 0.9214394+ 6.599344i
#> 10 1.0844101 7.282250 0.18 0.18 1.0844101+ 7.282250i
#> 11 1.0747601 7.843611 0.20 0.20 1.0747601+ 7.843611i
#> 12 1.1173678 8.487642 0.22 0.22 1.1173678+ 8.487642i
#> 13 1.2321889 9.095695 0.24 0.24 1.2321889+ 9.095695i
#> 14 1.2730578 9.626015 0.26 0.26 1.2730578+ 9.626015i
#> 15 1.3780316 10.294571 0.28 0.28 1.3780316+10.294571i
#> 16 1.5554000 10.856981 0.30 0.30 1.5554000+10.856981i
#> 17 1.6624462 11.463080 0.32 0.32 1.6624462+11.463080i
#> 18 1.6953847 12.014610 0.34 0.34 1.6953847+12.014610i
#> 19 1.8698072 12.570772 0.36 0.36 1.8698072+12.570772i
#> 20 1.9773604 13.097563 0.38 0.38 1.9773604+13.097563i
#> 21 1.9611258 13.783869 0.40 0.40 1.9611258+13.783869i
#> 22 1.9543134 14.251527 0.42 0.42 1.9543134+14.251527i
#> 23 1.9898254 14.888013 0.44 0.44 1.9898254+14.888013i
#> 24 2.0846756 15.426896 0.46 0.46 2.0846756+15.426896i
#> displacement Trajectory Simulation TrajSim
#> 1 0.000000000+0.0000000i Traj_2 Sim_2 TrajSim_2_2
#> 2 0.020340701+0.6997403i Traj_2 Sim_2 TrajSim_2_2
#> 3 0.106250708+0.6174771i Traj_2 Sim_2 TrajSim_2_2
#> 4 0.184008661+0.5640121i Traj_2 Sim_2 TrajSim_2_2
#> 5 0.036334584+0.7556728i Traj_2 Sim_2 TrajSim_2_2
#> 6 0.012604982+0.5342816i Traj_2 Sim_2 TrajSim_2_2
#> 7 0.155329767+0.5762705i Traj_2 Sim_2 TrajSim_2_2
#> 8 0.062092435+0.6216277i Traj_2 Sim_2 TrajSim_2_2
#> 9 0.008477529+0.6702616i Traj_2 Sim_2 TrajSim_2_2
#> 10 0.162970733+0.6829065i Traj_2 Sim_2 TrajSim_2_2
#> 11 -0.009649977+0.5613613i Traj_2 Sim_2 TrajSim_2_2
#> 12 0.042607638+0.6440303i Traj_2 Sim_2 TrajSim_2_2
#> 13 0.114821098+0.6080531i Traj_2 Sim_2 TrajSim_2_2
#> 14 0.040868917+0.5303203i Traj_2 Sim_2 TrajSim_2_2
#> 15 0.104973823+0.6685559i Traj_2 Sim_2 TrajSim_2_2
#> 16 0.177368413+0.5624097i Traj_2 Sim_2 TrajSim_2_2
#> 17 0.107046156+0.6060995i Traj_2 Sim_2 TrajSim_2_2
#> 18 0.032938556+0.5515294i Traj_2 Sim_2 TrajSim_2_2
#> 19 0.174422475+0.5561623i Traj_2 Sim_2 TrajSim_2_2
#> 20 0.107553202+0.5267911i Traj_2 Sim_2 TrajSim_2_2
#> 21 -0.016234569+0.6863061i Traj_2 Sim_2 TrajSim_2_2
#> 22 -0.006812467+0.4676577i Traj_2 Sim_2 TrajSim_2_2
#> 23 0.035511999+0.6364863i Traj_2 Sim_2 TrajSim_2_2
#> 24 0.094850265+0.5388828i Traj_2 Sim_2 TrajSim_2_2
#>
#>
#> [[3]]
#> [[3]][[1]]
#> x y time displacementTime polar
#> 1 0.6960000 0.946000 0.00 0.00 0.6960000+ 0.946000i
#> 2 0.7245842 1.497420 0.02 0.02 0.7245842+ 1.497420i
#> 3 0.7891861 2.084564 0.04 0.04 0.7891861+ 2.084564i
#> 4 0.7654408 2.628768 0.06 0.06 0.7654408+ 2.628768i
#> 5 0.7582952 3.144512 0.08 0.08 0.7582952+ 3.144512i
#> 6 0.8728104 3.657280 0.10 0.10 0.8728104+ 3.657280i
#> 7 0.9955728 4.174679 0.12 0.12 0.9955728+ 4.174679i
#> 8 1.1272204 4.586555 0.14 0.14 1.1272204+ 4.586555i
#> 9 1.1573979 5.122354 0.16 0.16 1.1573979+ 5.122354i
#> 10 1.0958244 5.735799 0.18 0.18 1.0958244+ 5.735799i
#> 11 1.2006222 6.264656 0.20 0.20 1.2006222+ 6.264656i
#> 12 1.1543318 6.828607 0.22 0.22 1.1543318+ 6.828607i
#> 13 1.3040716 7.295057 0.24 0.24 1.3040716+ 7.295057i
#> 14 1.4098700 7.793589 0.26 0.26 1.4098700+ 7.793589i
#> 15 1.2639847 8.277011 0.28 0.28 1.2639847+ 8.277011i
#> 16 1.3035341 8.871562 0.30 0.30 1.3035341+ 8.871562i
#> 17 1.4175738 9.522809 0.32 0.32 1.4175738+ 9.522809i
#> 18 1.2774735 10.060690 0.34 0.34 1.2774735+10.060690i
#> 19 1.2977332 10.539530 0.36 0.36 1.2977332+10.539530i
#> 20 1.3862539 11.086587 0.38 0.38 1.3862539+11.086587i
#> 21 1.3866467 11.587236 0.40 0.40 1.3866467+11.587236i
#> 22 1.3696914 12.099376 0.42 0.42 1.3696914+12.099376i
#> 23 1.4352612 12.631356 0.44 0.44 1.4352612+12.631356i
#> 24 1.4361423 13.151876 0.46 0.46 1.4361423+13.151876i
#> 25 1.5577380 13.709390 0.48 0.48 1.5577380+13.709390i
#> 26 1.6857885 14.198563 0.50 0.50 1.6857885+14.198563i
#> 27 1.7220397 14.753071 0.52 0.52 1.7220397+14.753071i
#> 28 1.6241639 15.268255 0.54 0.54 1.6241639+15.268255i
#> 29 1.6826483 15.818238 0.56 0.56 1.6826483+15.818238i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000000+0.0000000i Traj_1 Sim_3 TrajSim_1_3
#> 2 0.0285842314+0.5514199i Traj_1 Sim_3 TrajSim_1_3
#> 3 0.0646018968+0.5871437i Traj_1 Sim_3 TrajSim_1_3
#> 4 -0.0237453191+0.5442050i Traj_1 Sim_3 TrajSim_1_3
#> 5 -0.0071455761+0.5157430i Traj_1 Sim_3 TrajSim_1_3
#> 6 0.1145151753+0.5127686i Traj_1 Sim_3 TrajSim_1_3
#> 7 0.1227623837+0.5173986i Traj_1 Sim_3 TrajSim_1_3
#> 8 0.1316475964+0.4118760i Traj_1 Sim_3 TrajSim_1_3
#> 9 0.0301774737+0.5357990i Traj_1 Sim_3 TrajSim_1_3
#> 10 -0.0615734653+0.6134452i Traj_1 Sim_3 TrajSim_1_3
#> 11 0.1047978311+0.5288568i Traj_1 Sim_3 TrajSim_1_3
#> 12 -0.0462904409+0.5639513i Traj_1 Sim_3 TrajSim_1_3
#> 13 0.1497397943+0.4664500i Traj_1 Sim_3 TrajSim_1_3
#> 14 0.1057983928+0.4985321i Traj_1 Sim_3 TrajSim_1_3
#> 15 -0.1458853134+0.4834220i Traj_1 Sim_3 TrajSim_1_3
#> 16 0.0395494320+0.5945512i Traj_1 Sim_3 TrajSim_1_3
#> 17 0.1140396624+0.6512466i Traj_1 Sim_3 TrajSim_1_3
#> 18 -0.1401002506+0.5378809i Traj_1 Sim_3 TrajSim_1_3
#> 19 0.0202596582+0.4788397i Traj_1 Sim_3 TrajSim_1_3
#> 20 0.0885207683+0.5470577i Traj_1 Sim_3 TrajSim_1_3
#> 21 0.0003927748+0.5006483i Traj_1 Sim_3 TrajSim_1_3
#> 22 -0.0169552892+0.5121400i Traj_1 Sim_3 TrajSim_1_3
#> 23 0.0655697729+0.5319798i Traj_1 Sim_3 TrajSim_1_3
#> 24 0.0008811285+0.5205201i Traj_1 Sim_3 TrajSim_1_3
#> 25 0.1215956391+0.5575140i Traj_1 Sim_3 TrajSim_1_3
#> 26 0.1280505437+0.4891736i Traj_1 Sim_3 TrajSim_1_3
#> 27 0.0362512269+0.5545080i Traj_1 Sim_3 TrajSim_1_3
#> 28 -0.0978758568+0.5151837i Traj_1 Sim_3 TrajSim_1_3
#> 29 0.0584844485+0.5499829i Traj_1 Sim_3 TrajSim_1_3
#>
#> [[3]][[2]]
#> x y time displacementTime polar
#> 1 0.3360000 1.560000 0.00 0.00 0.3360000+ 1.560000i
#> 2 0.4573436 2.135325 0.02 0.02 0.4573436+ 2.135325i
#> 3 0.6576219 2.713777 0.04 0.04 0.6576219+ 2.713777i
#> 4 0.8779878 3.308134 0.06 0.06 0.8779878+ 3.308134i
#> 5 0.9878742 3.878186 0.08 0.08 0.9878742+ 3.878186i
#> 6 1.1569755 4.612970 0.10 0.10 1.1569755+ 4.612970i
#> 7 1.0048975 5.216548 0.12 0.12 1.0048975+ 5.216548i
#> 8 1.1217057 5.836823 0.14 0.14 1.1217057+ 5.836823i
#> 9 1.2931938 6.548481 0.16 0.16 1.2931938+ 6.548481i
#> 10 1.3037445 7.275076 0.18 0.18 1.3037445+ 7.275076i
#> 11 1.3638253 7.808392 0.20 0.20 1.3638253+ 7.808392i
#> 12 1.6255602 8.396008 0.22 0.22 1.6255602+ 8.396008i
#> 13 1.7097197 8.964708 0.24 0.24 1.7097197+ 8.964708i
#> 14 1.5431576 9.628379 0.26 0.26 1.5431576+ 9.628379i
#> 15 1.5378856 10.278009 0.28 0.28 1.5378856+10.278009i
#> 16 1.6399095 10.830468 0.30 0.30 1.6399095+10.830468i
#> 17 1.7102265 11.390646 0.32 0.32 1.7102265+11.390646i
#> 18 1.7200138 11.957941 0.34 0.34 1.7200138+11.957941i
#> 19 1.9505013 12.526532 0.36 0.36 1.9505013+12.526532i
#> 20 2.2430110 13.148611 0.38 0.38 2.2430110+13.148611i
#> 21 2.3615519 13.682574 0.40 0.40 2.3615519+13.682574i
#> 22 2.5630802 14.264985 0.42 0.42 2.5630802+14.264985i
#> 23 2.6512245 14.792080 0.44 0.44 2.6512245+14.792080i
#> 24 2.7302442 15.517927 0.46 0.46 2.7302442+15.517927i
#> displacement Trajectory Simulation TrajSim
#> 1 0.000000000+0.0000000i Traj_2 Sim_3 TrajSim_2_3
#> 2 0.121343589+0.5753254i Traj_2 Sim_3 TrajSim_2_3
#> 3 0.200278291+0.5784517i Traj_2 Sim_3 TrajSim_2_3
#> 4 0.220365943+0.5943570i Traj_2 Sim_3 TrajSim_2_3
#> 5 0.109886348+0.5700522i Traj_2 Sim_3 TrajSim_2_3
#> 6 0.169101362+0.7347839i Traj_2 Sim_3 TrajSim_2_3
#> 7 -0.152078026+0.6035780i Traj_2 Sim_3 TrajSim_2_3
#> 8 0.116808189+0.6202750i Traj_2 Sim_3 TrajSim_2_3
#> 9 0.171488109+0.7116574i Traj_2 Sim_3 TrajSim_2_3
#> 10 0.010550673+0.7265952i Traj_2 Sim_3 TrajSim_2_3
#> 11 0.060080806+0.5333166i Traj_2 Sim_3 TrajSim_2_3
#> 12 0.261734925+0.5876152i Traj_2 Sim_3 TrajSim_2_3
#> 13 0.084159476+0.5687002i Traj_2 Sim_3 TrajSim_2_3
#> 14 -0.166562134+0.6636716i Traj_2 Sim_3 TrajSim_2_3
#> 15 -0.005271990+0.6496301i Traj_2 Sim_3 TrajSim_2_3
#> 16 0.102023943+0.5524583i Traj_2 Sim_3 TrajSim_2_3
#> 17 0.070316947+0.5601780i Traj_2 Sim_3 TrajSim_2_3
#> 18 0.009787386+0.5672949i Traj_2 Sim_3 TrajSim_2_3
#> 19 0.230487448+0.5685919i Traj_2 Sim_3 TrajSim_2_3
#> 20 0.292509755+0.6220781i Traj_2 Sim_3 TrajSim_2_3
#> 21 0.118540899+0.5339637i Traj_2 Sim_3 TrajSim_2_3
#> 22 0.201528295+0.5824108i Traj_2 Sim_3 TrajSim_2_3
#> 23 0.088144219+0.5270946i Traj_2 Sim_3 TrajSim_2_3
#> 24 0.079019786+0.7258478i Traj_2 Sim_3 TrajSim_2_3
#>
#>
#> [[4]]
#> [[4]][[1]]
#> x y time displacementTime polar
#> 1 0.6960000 0.946000 0.00 0.00 0.6960000+ 0.946000i
#> 2 0.7090360 1.531942 0.02 0.02 0.7090360+ 1.531942i
#> 3 0.8456161 1.872507 0.04 0.04 0.8456161+ 1.872507i
#> 4 0.8222794 2.429700 0.06 0.06 0.8222794+ 2.429700i
#> 5 0.8535372 2.951137 0.08 0.08 0.8535372+ 2.951137i
#> 6 0.7881387 3.408645 0.10 0.10 0.7881387+ 3.408645i
#> 7 0.8186998 4.008301 0.12 0.12 0.8186998+ 4.008301i
#> 8 0.9162929 4.514881 0.14 0.14 0.9162929+ 4.514881i
#> 9 0.9634855 5.079340 0.16 0.16 0.9634855+ 5.079340i
#> 10 0.9456290 5.688445 0.18 0.18 0.9456290+ 5.688445i
#> 11 1.0650463 6.138498 0.20 0.20 1.0650463+ 6.138498i
#> 12 1.0915237 6.657216 0.22 0.22 1.0915237+ 6.657216i
#> 13 1.0938327 7.201211 0.24 0.24 1.0938327+ 7.201211i
#> 14 1.0571483 7.785608 0.26 0.26 1.0571483+ 7.785608i
#> 15 0.8700615 8.330402 0.28 0.28 0.8700615+ 8.330402i
#> 16 0.9242726 8.807067 0.30 0.30 0.9242726+ 8.807067i
#> 17 0.9887657 9.330221 0.32 0.32 0.9887657+ 9.330221i
#> 18 0.9802293 9.832654 0.34 0.34 0.9802293+ 9.832654i
#> 19 0.9544797 10.383597 0.36 0.36 0.9544797+10.383597i
#> 20 0.9693850 10.998641 0.38 0.38 0.9693850+10.998641i
#> 21 0.9723395 11.573791 0.40 0.40 0.9723395+11.573791i
#> 22 1.1857982 12.050138 0.42 0.42 1.1857982+12.050138i
#> 23 1.3272067 12.512645 0.44 0.44 1.3272067+12.512645i
#> 24 1.3263360 12.993009 0.46 0.46 1.3263360+12.993009i
#> 25 1.4987363 13.591153 0.48 0.48 1.4987363+13.591153i
#> 26 1.3880753 14.185923 0.50 0.50 1.3880753+14.185923i
#> 27 1.5235532 14.716019 0.52 0.52 1.5235532+14.716019i
#> 28 1.5210402 15.266657 0.54 0.54 1.5210402+15.266657i
#> 29 1.5558223 15.847241 0.56 0.56 1.5558223+15.847241i
#> displacement Trajectory Simulation TrajSim
#> 1 0.000000000+0.0000000i Traj_1 Sim_4 TrajSim_1_4
#> 2 0.013035982+0.5859416i Traj_1 Sim_4 TrajSim_1_4
#> 3 0.136580087+0.3405656i Traj_1 Sim_4 TrajSim_1_4
#> 4 -0.023336666+0.5571928i Traj_1 Sim_4 TrajSim_1_4
#> 5 0.031257811+0.5214374i Traj_1 Sim_4 TrajSim_1_4
#> 6 -0.065398533+0.4575074i Traj_1 Sim_4 TrajSim_1_4
#> 7 0.030561153+0.5996559i Traj_1 Sim_4 TrajSim_1_4
#> 8 0.097593021+0.5065800i Traj_1 Sim_4 TrajSim_1_4
#> 9 0.047192673+0.5644597i Traj_1 Sim_4 TrajSim_1_4
#> 10 -0.017856506+0.6091047i Traj_1 Sim_4 TrajSim_1_4
#> 11 0.119417262+0.4500534i Traj_1 Sim_4 TrajSim_1_4
#> 12 0.026477411+0.5187176i Traj_1 Sim_4 TrajSim_1_4
#> 13 0.002309000+0.5439946i Traj_1 Sim_4 TrajSim_1_4
#> 14 -0.036684436+0.5843978i Traj_1 Sim_4 TrajSim_1_4
#> 15 -0.187086722+0.5447939i Traj_1 Sim_4 TrajSim_1_4
#> 16 0.054211098+0.4766642i Traj_1 Sim_4 TrajSim_1_4
#> 17 0.064493044+0.5231544i Traj_1 Sim_4 TrajSim_1_4
#> 18 -0.008536357+0.5024327i Traj_1 Sim_4 TrajSim_1_4
#> 19 -0.025749593+0.5509435i Traj_1 Sim_4 TrajSim_1_4
#> 20 0.014905234+0.6150439i Traj_1 Sim_4 TrajSim_1_4
#> 21 0.002954552+0.5751501i Traj_1 Sim_4 TrajSim_1_4
#> 22 0.213458679+0.4763469i Traj_1 Sim_4 TrajSim_1_4
#> 23 0.141408461+0.4625067i Traj_1 Sim_4 TrajSim_1_4
#> 24 -0.000870696+0.4803639i Traj_1 Sim_4 TrajSim_1_4
#> 25 0.172400344+0.5981441i Traj_1 Sim_4 TrajSim_1_4
#> 26 -0.110661001+0.5947707i Traj_1 Sim_4 TrajSim_1_4
#> 27 0.135477927+0.5300954i Traj_1 Sim_4 TrajSim_1_4
#> 28 -0.002513040+0.5506382i Traj_1 Sim_4 TrajSim_1_4
#> 29 0.034782149+0.5805844i Traj_1 Sim_4 TrajSim_1_4
#>
#> [[4]][[2]]
#> x y time displacementTime polar
#> 1 0.3360000 1.560000 0.00 0.00 0.3360000+ 1.560000i
#> 2 0.3394796 2.322207 0.02 0.02 0.3394796+ 2.322207i
#> 3 0.4398166 2.993439 0.04 0.04 0.4398166+ 2.993439i
#> 4 0.5568283 3.458742 0.06 0.06 0.5568283+ 3.458742i
#> 5 0.6721943 4.110261 0.08 0.08 0.6721943+ 4.110261i
#> 6 0.7509576 4.804669 0.10 0.10 0.7509576+ 4.804669i
#> 7 0.9271915 5.501759 0.12 0.12 0.9271915+ 5.501759i
#> 8 0.9320638 6.204972 0.14 0.14 0.9320638+ 6.204972i
#> 9 1.0428208 6.720669 0.16 0.16 1.0428208+ 6.720669i
#> 10 1.1460252 7.201356 0.18 0.18 1.1460252+ 7.201356i
#> 11 1.2388667 7.687668 0.20 0.20 1.2388667+ 7.687668i
#> 12 1.3052467 8.288712 0.22 0.22 1.3052467+ 8.288712i
#> 13 1.2508120 9.027556 0.24 0.24 1.2508120+ 9.027556i
#> 14 1.3057291 9.662740 0.26 0.26 1.3057291+ 9.662740i
#> 15 1.1478362 10.283946 0.28 0.28 1.1478362+10.283946i
#> 16 1.2795524 10.850898 0.30 0.30 1.2795524+10.850898i
#> 17 1.4339777 11.467878 0.32 0.32 1.4339777+11.467878i
#> 18 1.5142217 12.055430 0.34 0.34 1.5142217+12.055430i
#> 19 1.6971738 12.662689 0.36 0.36 1.6971738+12.662689i
#> 20 1.7003595 13.253258 0.38 0.38 1.7003595+13.253258i
#> 21 1.8678199 13.940412 0.40 0.40 1.8678199+13.940412i
#> 22 2.0016150 14.431644 0.42 0.42 2.0016150+14.431644i
#> 23 1.9811723 14.855775 0.44 0.44 1.9811723+14.855775i
#> 24 2.1735860 15.401520 0.46 0.46 2.1735860+15.401520i
#> displacement Trajectory Simulation TrajSim
#> 1 0.000000000+0.0000000i Traj_2 Sim_4 TrajSim_2_4
#> 2 0.003479570+0.7622069i Traj_2 Sim_4 TrajSim_2_4
#> 3 0.100337008+0.6712318i Traj_2 Sim_4 TrajSim_2_4
#> 4 0.117011706+0.4653038i Traj_2 Sim_4 TrajSim_2_4
#> 5 0.115366012+0.6515182i Traj_2 Sim_4 TrajSim_2_4
#> 6 0.078763267+0.6944085i Traj_2 Sim_4 TrajSim_2_4
#> 7 0.176233940+0.6970896i Traj_2 Sim_4 TrajSim_2_4
#> 8 0.004872295+0.7032127i Traj_2 Sim_4 TrajSim_2_4
#> 9 0.110757043+0.5156979i Traj_2 Sim_4 TrajSim_2_4
#> 10 0.103204378+0.4806870i Traj_2 Sim_4 TrajSim_2_4
#> 11 0.092841525+0.4863117i Traj_2 Sim_4 TrajSim_2_4
#> 12 0.066379956+0.6010435i Traj_2 Sim_4 TrajSim_2_4
#> 13 -0.054434670+0.7388445i Traj_2 Sim_4 TrajSim_2_4
#> 14 0.054917095+0.6351838i Traj_2 Sim_4 TrajSim_2_4
#> 15 -0.157892928+0.6212059i Traj_2 Sim_4 TrajSim_2_4
#> 16 0.131716168+0.5669519i Traj_2 Sim_4 TrajSim_2_4
#> 17 0.154425335+0.6169803i Traj_2 Sim_4 TrajSim_2_4
#> 18 0.080243998+0.5875518i Traj_2 Sim_4 TrajSim_2_4
#> 19 0.182952139+0.6072592i Traj_2 Sim_4 TrajSim_2_4
#> 20 0.003185695+0.5905687i Traj_2 Sim_4 TrajSim_2_4
#> 21 0.167460352+0.6871546i Traj_2 Sim_4 TrajSim_2_4
#> 22 0.133795073+0.4912316i Traj_2 Sim_4 TrajSim_2_4
#> 23 -0.020442617+0.4241315i Traj_2 Sim_4 TrajSim_2_4
#> 24 0.192413651+0.5457447i Traj_2 Sim_4 TrajSim_2_4
#>
#>
#> [[5]]
#> [[5]][[1]]
#> x y time displacementTime polar
#> 1 0.6960000 0.946000 0.00 0.00 0.6960000+ 0.946000i
#> 2 0.8199837 1.479172 0.02 0.02 0.8199837+ 1.479172i
#> 3 0.8149489 2.016667 0.04 0.04 0.8149489+ 2.016667i
#> 4 0.8873438 2.550559 0.06 0.06 0.8873438+ 2.550559i
#> 5 0.8443534 3.028033 0.08 0.08 0.8443534+ 3.028033i
#> 6 0.9215223 3.417415 0.10 0.10 0.9215223+ 3.417415i
#> 7 0.9723169 4.022998 0.12 0.12 0.9723169+ 4.022998i
#> 8 0.9953525 4.571820 0.14 0.14 0.9953525+ 4.571820i
#> 9 1.1282428 5.067572 0.16 0.16 1.1282428+ 5.067572i
#> 10 1.1917966 5.613130 0.18 0.18 1.1917966+ 5.613130i
#> 11 1.2005320 6.295111 0.20 0.20 1.2005320+ 6.295111i
#> 12 1.2389672 6.783378 0.22 0.22 1.2389672+ 6.783378i
#> 13 1.4996725 7.244100 0.24 0.24 1.4996725+ 7.244100i
#> 14 1.6699790 7.819310 0.26 0.26 1.6699790+ 7.819310i
#> 15 1.7213401 8.307329 0.28 0.28 1.7213401+ 8.307329i
#> 16 1.8423232 8.772151 0.30 0.30 1.8423232+ 8.772151i
#> 17 1.9600088 9.308106 0.32 0.32 1.9600088+ 9.308106i
#> 18 1.8697140 9.765496 0.34 0.34 1.8697140+ 9.765496i
#> 19 1.9662557 10.276222 0.36 0.36 1.9662557+10.276222i
#> 20 2.0479518 10.779269 0.38 0.38 2.0479518+10.779269i
#> 21 2.1420090 11.357270 0.40 0.40 2.1420090+11.357270i
#> 22 2.0868129 11.871479 0.42 0.42 2.0868129+11.871479i
#> 23 2.1164638 12.419469 0.44 0.44 2.1164638+12.419469i
#> 24 2.2258896 12.854032 0.46 0.46 2.2258896+12.854032i
#> 25 2.2892409 13.386806 0.48 0.48 2.2892409+13.386806i
#> 26 2.2696275 13.906695 0.50 0.50 2.2696275+13.906695i
#> 27 2.4858072 14.398486 0.52 0.52 2.4858072+14.398486i
#> 28 2.5406960 14.928594 0.54 0.54 2.5406960+14.928594i
#> 29 2.5791298 15.444722 0.56 0.56 2.5791298+15.444722i
#> displacement Trajectory Simulation TrajSim
#> 1 0.000000000+0.0000000i Traj_1 Sim_5 TrajSim_1_5
#> 2 0.123983734+0.5331717i Traj_1 Sim_5 TrajSim_1_5
#> 3 -0.005034826+0.5374956i Traj_1 Sim_5 TrajSim_1_5
#> 4 0.072394896+0.5338914i Traj_1 Sim_5 TrajSim_1_5
#> 5 -0.042990437+0.4774744i Traj_1 Sim_5 TrajSim_1_5
#> 6 0.077168981+0.3893815i Traj_1 Sim_5 TrajSim_1_5
#> 7 0.050794528+0.6055835i Traj_1 Sim_5 TrajSim_1_5
#> 8 0.023035666+0.5488220i Traj_1 Sim_5 TrajSim_1_5
#> 9 0.132890262+0.4957523i Traj_1 Sim_5 TrajSim_1_5
#> 10 0.063553829+0.5455574i Traj_1 Sim_5 TrajSim_1_5
#> 11 0.008735342+0.6819817i Traj_1 Sim_5 TrajSim_1_5
#> 12 0.038435227+0.4882670i Traj_1 Sim_5 TrajSim_1_5
#> 13 0.260705281+0.4607214i Traj_1 Sim_5 TrajSim_1_5
#> 14 0.170306485+0.5752096i Traj_1 Sim_5 TrajSim_1_5
#> 15 0.051361103+0.4880199i Traj_1 Sim_5 TrajSim_1_5
#> 16 0.120983094+0.4648214i Traj_1 Sim_5 TrajSim_1_5
#> 17 0.117685644+0.5359551i Traj_1 Sim_5 TrajSim_1_5
#> 18 -0.090294773+0.4573900i Traj_1 Sim_5 TrajSim_1_5
#> 19 0.096541664+0.5107264i Traj_1 Sim_5 TrajSim_1_5
#> 20 0.081696113+0.5030463i Traj_1 Sim_5 TrajSim_1_5
#> 21 0.094057169+0.5780016i Traj_1 Sim_5 TrajSim_1_5
#> 22 -0.055196122+0.5142085i Traj_1 Sim_5 TrajSim_1_5
#> 23 0.029650958+0.5479905i Traj_1 Sim_5 TrajSim_1_5
#> 24 0.109425794+0.4345632i Traj_1 Sim_5 TrajSim_1_5
#> 25 0.063351290+0.5327734i Traj_1 Sim_5 TrajSim_1_5
#> 26 -0.019613376+0.5198894i Traj_1 Sim_5 TrajSim_1_5
#> 27 0.216179665+0.4917910i Traj_1 Sim_5 TrajSim_1_5
#> 28 0.054888844+0.5301078i Traj_1 Sim_5 TrajSim_1_5
#> 29 0.038433784+0.5161276i Traj_1 Sim_5 TrajSim_1_5
#>
#> [[5]][[2]]
#> x y time displacementTime polar
#> 1 0.3360000 1.560000 0.00 0.00 0.3360000+ 1.560000i
#> 2 0.3476851 2.049673 0.02 0.02 0.3476851+ 2.049673i
#> 3 0.3705892 2.671130 0.04 0.04 0.3705892+ 2.671130i
#> 4 0.4476197 3.279935 0.06 0.06 0.4476197+ 3.279935i
#> 5 0.5113364 3.884578 0.08 0.08 0.5113364+ 3.884578i
#> 6 0.6356747 4.680311 0.10 0.10 0.6356747+ 4.680311i
#> 7 0.7137826 5.253755 0.12 0.12 0.7137826+ 5.253755i
#> 8 0.6838414 5.926666 0.14 0.14 0.6838414+ 5.926666i
#> 9 0.8092582 6.652703 0.16 0.16 0.8092582+ 6.652703i
#> 10 0.8394962 7.323790 0.18 0.18 0.8394962+ 7.323790i
#> 11 0.9243582 7.855747 0.20 0.20 0.9243582+ 7.855747i
#> 12 1.0108437 8.612983 0.22 0.22 1.0108437+ 8.612983i
#> 13 1.0465962 9.218924 0.24 0.24 1.0465962+ 9.218924i
#> 14 1.0471641 9.964173 0.26 0.26 1.0471641+ 9.964173i
#> 15 1.0745780 10.493824 0.28 0.28 1.0745780+10.493824i
#> 16 1.1635856 11.015806 0.30 0.30 1.1635856+11.015806i
#> 17 1.0854160 11.504643 0.32 0.32 1.0854160+11.504643i
#> 18 1.2294689 12.132413 0.34 0.34 1.2294689+12.132413i
#> 19 1.4687825 12.741100 0.36 0.36 1.4687825+12.741100i
#> 20 1.5290429 13.321597 0.38 0.38 1.5290429+13.321597i
#> 21 1.5449115 13.840314 0.40 0.40 1.5449115+13.840314i
#> 22 1.6299685 14.552172 0.42 0.42 1.6299685+14.552172i
#> 23 1.7599435 15.030304 0.44 0.44 1.7599435+15.030304i
#> 24 1.9366733 15.638846 0.46 0.46 1.9366733+15.638846i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000000+0.0000000i Traj_2 Sim_5 TrajSim_2_5
#> 2 0.0116851180+0.4896734i Traj_2 Sim_5 TrajSim_2_5
#> 3 0.0229041265+0.6214564i Traj_2 Sim_5 TrajSim_2_5
#> 4 0.0770304333+0.6088052i Traj_2 Sim_5 TrajSim_2_5
#> 5 0.0637166957+0.6046433i Traj_2 Sim_5 TrajSim_2_5
#> 6 0.1243383463+0.7957326i Traj_2 Sim_5 TrajSim_2_5
#> 7 0.0781079198+0.5734439i Traj_2 Sim_5 TrajSim_2_5
#> 8 -0.0299412439+0.6729116i Traj_2 Sim_5 TrajSim_2_5
#> 9 0.1254168347+0.7260364i Traj_2 Sim_5 TrajSim_2_5
#> 10 0.0302379220+0.6710874i Traj_2 Sim_5 TrajSim_2_5
#> 11 0.0848620102+0.5319571i Traj_2 Sim_5 TrajSim_2_5
#> 12 0.0864855386+0.7572352i Traj_2 Sim_5 TrajSim_2_5
#> 13 0.0357524659+0.6059418i Traj_2 Sim_5 TrajSim_2_5
#> 14 0.0005678872+0.7452491i Traj_2 Sim_5 TrajSim_2_5
#> 15 0.0274139327+0.5296509i Traj_2 Sim_5 TrajSim_2_5
#> 16 0.0890076339+0.5219814i Traj_2 Sim_5 TrajSim_2_5
#> 17 -0.0781696010+0.4888378i Traj_2 Sim_5 TrajSim_2_5
#> 18 0.1440528954+0.6277693i Traj_2 Sim_5 TrajSim_2_5
#> 19 0.2393135812+0.6086869i Traj_2 Sim_5 TrajSim_2_5
#> 20 0.0602604275+0.5804976i Traj_2 Sim_5 TrajSim_2_5
#> 21 0.0158685713+0.5187169i Traj_2 Sim_5 TrajSim_2_5
#> 22 0.0850569936+0.7118582i Traj_2 Sim_5 TrajSim_2_5
#> 23 0.1299750599+0.4781316i Traj_2 Sim_5 TrajSim_2_5
#> 24 0.1767297897+0.6085415i Traj_2 Sim_5 TrajSim_2_5
#>
#>
#> [[6]]
#> [[6]][[1]]
#> x y time displacementTime polar
#> 1 0.6960000 0.946000 0.00 0.00 0.6960000+ 0.946000i
#> 2 0.7024341 1.469733 0.02 0.02 0.7024341+ 1.469733i
#> 3 0.9697602 1.904479 0.04 0.04 0.9697602+ 1.904479i
#> 4 1.0344870 2.477479 0.06 0.06 1.0344870+ 2.477479i
#> 5 1.1004840 3.073469 0.08 0.08 1.1004840+ 3.073469i
#> 6 1.1147690 3.621854 0.10 0.10 1.1147690+ 3.621854i
#> 7 1.1318177 4.219889 0.12 0.12 1.1318177+ 4.219889i
#> 8 1.2281327 4.768539 0.14 0.14 1.2281327+ 4.768539i
#> 9 1.2379030 5.270096 0.16 0.16 1.2379030+ 5.270096i
#> 10 1.2805937 5.725715 0.18 0.18 1.2805937+ 5.725715i
#> 11 1.3006790 6.322175 0.20 0.20 1.3006790+ 6.322175i
#> 12 1.3365950 6.938036 0.22 0.22 1.3365950+ 6.938036i
#> 13 1.2888612 7.492418 0.24 0.24 1.2888612+ 7.492418i
#> 14 1.1455336 8.138266 0.26 0.26 1.1455336+ 8.138266i
#> 15 1.0318460 8.718243 0.28 0.28 1.0318460+ 8.718243i
#> 16 1.1455335 9.155270 0.30 0.30 1.1455335+ 9.155270i
#> 17 1.1074425 9.682895 0.32 0.32 1.1074425+ 9.682895i
#> 18 1.1928068 10.245524 0.34 0.34 1.1928068+10.245524i
#> 19 1.2520920 10.693643 0.36 0.36 1.2520920+10.693643i
#> 20 1.3055070 11.234147 0.38 0.38 1.3055070+11.234147i
#> 21 1.3360543 11.804527 0.40 0.40 1.3360543+11.804527i
#> 22 1.3640983 12.303842 0.42 0.42 1.3640983+12.303842i
#> 23 1.3092299 12.884353 0.44 0.44 1.3092299+12.884353i
#> 24 1.4608146 13.483674 0.46 0.46 1.4608146+13.483674i
#> 25 1.4545066 14.027174 0.48 0.48 1.4545066+14.027174i
#> 26 1.4869014 14.555656 0.50 0.50 1.4869014+14.555656i
#> 27 1.6276316 15.007137 0.52 0.52 1.6276316+15.007137i
#> 28 1.6370530 15.546921 0.54 0.54 1.6370530+15.546921i
#> 29 1.4724040 16.016012 0.56 0.56 1.4724040+16.016012i
#> displacement Trajectory Simulation TrajSim
#> 1 0.000000000+0.0000000i Traj_1 Sim_6 TrajSim_1_6
#> 2 0.006434051+0.5237327i Traj_1 Sim_6 TrajSim_1_6
#> 3 0.267326135+0.4347463i Traj_1 Sim_6 TrajSim_1_6
#> 4 0.064726834+0.5730002i Traj_1 Sim_6 TrajSim_1_6
#> 5 0.065997004+0.5959903i Traj_1 Sim_6 TrajSim_1_6
#> 6 0.014284971+0.5483843i Traj_1 Sim_6 TrajSim_1_6
#> 7 0.017048668+0.5980356i Traj_1 Sim_6 TrajSim_1_6
#> 8 0.096315074+0.5486498i Traj_1 Sim_6 TrajSim_1_6
#> 9 0.009770281+0.5015563i Traj_1 Sim_6 TrajSim_1_6
#> 10 0.042690653+0.4556192i Traj_1 Sim_6 TrajSim_1_6
#> 11 0.020085349+0.5964601i Traj_1 Sim_6 TrajSim_1_6
#> 12 0.035915944+0.6158613i Traj_1 Sim_6 TrajSim_1_6
#> 13 -0.047733746+0.5543824i Traj_1 Sim_6 TrajSim_1_6
#> 14 -0.143327616+0.6458478i Traj_1 Sim_6 TrajSim_1_6
#> 15 -0.113687623+0.5799765i Traj_1 Sim_6 TrajSim_1_6
#> 16 0.113687501+0.4370276i Traj_1 Sim_6 TrajSim_1_6
#> 17 -0.038090931+0.5276244i Traj_1 Sim_6 TrajSim_1_6
#> 18 0.085364260+0.5626292i Traj_1 Sim_6 TrajSim_1_6
#> 19 0.059285187+0.4481188i Traj_1 Sim_6 TrajSim_1_6
#> 20 0.053414962+0.5405044i Traj_1 Sim_6 TrajSim_1_6
#> 21 0.030547388+0.5703795i Traj_1 Sim_6 TrajSim_1_6
#> 22 0.028043944+0.4993150i Traj_1 Sim_6 TrajSim_1_6
#> 23 -0.054868368+0.5805115i Traj_1 Sim_6 TrajSim_1_6
#> 24 0.151584630+0.5993209i Traj_1 Sim_6 TrajSim_1_6
#> 25 -0.006307930+0.5435003i Traj_1 Sim_6 TrajSim_1_6
#> 26 0.032394782+0.5284815i Traj_1 Sim_6 TrajSim_1_6
#> 27 0.140730218+0.4514814i Traj_1 Sim_6 TrajSim_1_6
#> 28 0.009421427+0.5397836i Traj_1 Sim_6 TrajSim_1_6
#> 29 -0.164649045+0.4690914i Traj_1 Sim_6 TrajSim_1_6
#>
#> [[6]][[2]]
#> x y time displacementTime polar
#> 1 0.3360000 1.560000 0.00 0.00 0.3360000+ 1.560000i
#> 2 0.3044999 2.143174 0.02 0.02 0.3044999+ 2.143174i
#> 3 0.4200030 2.847462 0.04 0.04 0.4200030+ 2.847462i
#> 4 0.4958713 3.395930 0.06 0.06 0.4958713+ 3.395930i
#> 5 0.5173971 3.993125 0.08 0.08 0.5173971+ 3.993125i
#> 6 0.4918780 4.663149 0.10 0.10 0.4918780+ 4.663149i
#> 7 0.4630742 5.287256 0.12 0.12 0.4630742+ 5.287256i
#> 8 0.3910809 5.844465 0.14 0.14 0.3910809+ 5.844465i
#> 9 0.3704898 6.381893 0.16 0.16 0.3704898+ 6.381893i
#> 10 0.4587032 7.046087 0.18 0.18 0.4587032+ 7.046087i
#> 11 0.4882589 7.614881 0.20 0.20 0.4882589+ 7.614881i
#> 12 0.4262628 8.261938 0.22 0.22 0.4262628+ 8.261938i
#> 13 0.4934107 8.896035 0.24 0.24 0.4934107+ 8.896035i
#> 14 0.4844548 9.588085 0.26 0.26 0.4844548+ 9.588085i
#> 15 0.6248489 10.146246 0.28 0.28 0.6248489+10.146246i
#> 16 0.7273189 10.811408 0.30 0.30 0.7273189+10.811408i
#> 17 0.7983159 11.315792 0.32 0.32 0.7983159+11.315792i
#> 18 0.7952043 11.970634 0.34 0.34 0.7952043+11.970634i
#> 19 0.8362798 12.513372 0.36 0.36 0.8362798+12.513372i
#> 20 1.0467873 13.236801 0.38 0.38 1.0467873+13.236801i
#> 21 1.2285012 13.860795 0.40 0.40 1.2285012+13.860795i
#> 22 1.2999932 14.479495 0.42 0.42 1.2999932+14.479495i
#> 23 1.3388262 14.927165 0.44 0.44 1.3388262+14.927165i
#> 24 1.4521784 15.343516 0.46 0.46 1.4521784+15.343516i
#> displacement Trajectory Simulation TrajSim
#> 1 0.000000000+0.0000000i Traj_2 Sim_6 TrajSim_2_6
#> 2 -0.031500089+0.5831742i Traj_2 Sim_6 TrajSim_2_6
#> 3 0.115503125+0.7042873i Traj_2 Sim_6 TrajSim_2_6
#> 4 0.075868235+0.5484689i Traj_2 Sim_6 TrajSim_2_6
#> 5 0.021525826+0.5971948i Traj_2 Sim_6 TrajSim_2_6
#> 6 -0.025519141+0.6700241i Traj_2 Sim_6 TrajSim_2_6
#> 7 -0.028803766+0.6241069i Traj_2 Sim_6 TrajSim_2_6
#> 8 -0.071993255+0.5572085i Traj_2 Sim_6 TrajSim_2_6
#> 9 -0.020591142+0.5374279i Traj_2 Sim_6 TrajSim_2_6
#> 10 0.088213402+0.6641942i Traj_2 Sim_6 TrajSim_2_6
#> 11 0.029555672+0.5687939i Traj_2 Sim_6 TrajSim_2_6
#> 12 -0.061996023+0.6470569i Traj_2 Sim_6 TrajSim_2_6
#> 13 0.067147898+0.6340969i Traj_2 Sim_6 TrajSim_2_6
#> 14 -0.008955920+0.6920504i Traj_2 Sim_6 TrajSim_2_6
#> 15 0.140394040+0.5581613i Traj_2 Sim_6 TrajSim_2_6
#> 16 0.102470004+0.6651613i Traj_2 Sim_6 TrajSim_2_6
#> 17 0.070997012+0.5043844i Traj_2 Sim_6 TrajSim_2_6
#> 18 -0.003111566+0.6548417i Traj_2 Sim_6 TrajSim_2_6
#> 19 0.041075533+0.5427380i Traj_2 Sim_6 TrajSim_2_6
#> 20 0.210507414+0.7234292i Traj_2 Sim_6 TrajSim_2_6
#> 21 0.181713954+0.6239937i Traj_2 Sim_6 TrajSim_2_6
#> 22 0.071492024+0.6187000i Traj_2 Sim_6 TrajSim_2_6
#> 23 0.038833012+0.4476700i Traj_2 Sim_6 TrajSim_2_6
#> 24 0.113352106+0.4163513i Traj_2 Sim_6 TrajSim_2_6
#>
#>
#> [[7]]
#> [[7]][[1]]
#> x y time displacementTime polar
#> 1 0.6960000 0.946000 0.00 0.00 0.6960000+ 0.946000i
#> 2 0.7444741 1.547518 0.02 0.02 0.7444741+ 1.547518i
#> 3 0.6112821 2.020726 0.04 0.04 0.6112821+ 2.020726i
#> 4 0.6641233 2.410754 0.06 0.06 0.6641233+ 2.410754i
#> 5 0.6844647 3.029628 0.08 0.08 0.6844647+ 3.029628i
#> 6 0.7231014 3.608800 0.10 0.10 0.7231014+ 3.608800i
#> 7 0.8634985 4.032093 0.12 0.12 0.8634985+ 4.032093i
#> 8 0.9832381 4.617609 0.14 0.14 0.9832381+ 4.617609i
#> 9 1.0879985 5.111883 0.16 0.16 1.0879985+ 5.111883i
#> 10 0.9811368 5.626775 0.18 0.18 0.9811368+ 5.626775i
#> 11 0.9308572 6.173600 0.20 0.20 0.9308572+ 6.173600i
#> 12 0.9234001 6.823543 0.22 0.22 0.9234001+ 6.823543i
#> 13 1.0659581 7.477339 0.24 0.24 1.0659581+ 7.477339i
#> 14 1.1818845 7.968476 0.26 0.26 1.1818845+ 7.968476i
#> 15 1.1977214 8.476541 0.28 0.28 1.1977214+ 8.476541i
#> 16 1.2410058 8.982788 0.30 0.30 1.2410058+ 8.982788i
#> 17 1.2274067 9.486658 0.32 0.32 1.2274067+ 9.486658i
#> 18 1.2522409 10.017950 0.34 0.34 1.2522409+10.017950i
#> 19 1.3053714 10.572945 0.36 0.36 1.3053714+10.572945i
#> 20 1.4187526 11.123350 0.38 0.38 1.4187526+11.123350i
#> 21 1.5755713 11.759897 0.40 0.40 1.5755713+11.759897i
#> 22 1.6176053 12.262191 0.42 0.42 1.6176053+12.262191i
#> 23 1.6619631 12.816135 0.44 0.44 1.6619631+12.816135i
#> 24 1.6389970 13.321161 0.46 0.46 1.6389970+13.321161i
#> 25 1.5817264 13.864472 0.48 0.48 1.5817264+13.864472i
#> 26 1.6178378 14.402421 0.50 0.50 1.6178378+14.402421i
#> 27 1.8234953 14.929068 0.52 0.52 1.8234953+14.929068i
#> 28 1.8510878 15.521042 0.54 0.54 1.8510878+15.521042i
#> 29 1.7990033 16.114780 0.56 0.56 1.7990033+16.114780i
#> displacement Trajectory Simulation TrajSim
#> 1 0.000000000+0.0000000i Traj_1 Sim_7 TrajSim_1_7
#> 2 0.048474050+0.6015182i Traj_1 Sim_7 TrajSim_1_7
#> 3 -0.133191956+0.4732083i Traj_1 Sim_7 TrajSim_1_7
#> 4 0.052841179+0.3900276i Traj_1 Sim_7 TrajSim_1_7
#> 5 0.020341441+0.6188735i Traj_1 Sim_7 TrajSim_1_7
#> 6 0.038636661+0.5791723i Traj_1 Sim_7 TrajSim_1_7
#> 7 0.140397170+0.4232926i Traj_1 Sim_7 TrajSim_1_7
#> 8 0.119739544+0.5855165i Traj_1 Sim_7 TrajSim_1_7
#> 9 0.104760392+0.4942737i Traj_1 Sim_7 TrajSim_1_7
#> 10 -0.106861716+0.5148920i Traj_1 Sim_7 TrajSim_1_7
#> 11 -0.050279555+0.5468249i Traj_1 Sim_7 TrajSim_1_7
#> 12 -0.007457144+0.6499430i Traj_1 Sim_7 TrajSim_1_7
#> 13 0.142558070+0.6537961i Traj_1 Sim_7 TrajSim_1_7
#> 14 0.115926341+0.4911371i Traj_1 Sim_7 TrajSim_1_7
#> 15 0.015836909+0.5080650i Traj_1 Sim_7 TrajSim_1_7
#> 16 0.043284445+0.5062470i Traj_1 Sim_7 TrajSim_1_7
#> 17 -0.013599143+0.5038697i Traj_1 Sim_7 TrajSim_1_7
#> 18 0.024834212+0.5312926i Traj_1 Sim_7 TrajSim_1_7
#> 19 0.053130524+0.5549944i Traj_1 Sim_7 TrajSim_1_7
#> 20 0.113381192+0.5504049i Traj_1 Sim_7 TrajSim_1_7
#> 21 0.156818647+0.6365472i Traj_1 Sim_7 TrajSim_1_7
#> 22 0.042034042+0.5022946i Traj_1 Sim_7 TrajSim_1_7
#> 23 0.044357806+0.5539437i Traj_1 Sim_7 TrajSim_1_7
#> 24 -0.022966152+0.5050255i Traj_1 Sim_7 TrajSim_1_7
#> 25 -0.057270537+0.5433116i Traj_1 Sim_7 TrajSim_1_7
#> 26 0.036111415+0.5379485i Traj_1 Sim_7 TrajSim_1_7
#> 27 0.205657430+0.5266474i Traj_1 Sim_7 TrajSim_1_7
#> 28 0.027592485+0.5919742i Traj_1 Sim_7 TrajSim_1_7
#> 29 -0.052084404+0.5937375i Traj_1 Sim_7 TrajSim_1_7
#>
#> [[7]][[2]]
#> x y time displacementTime polar
#> 1 0.3360000 1.560000 0.00 0.00 0.3360000+ 1.560000i
#> 2 0.4174830 2.024905 0.02 0.02 0.4174830+ 2.024905i
#> 3 0.5340160 2.722044 0.04 0.04 0.5340160+ 2.722044i
#> 4 0.7156943 3.467413 0.06 0.06 0.7156943+ 3.467413i
#> 5 0.7923288 4.070007 0.08 0.08 0.7923288+ 4.070007i
#> 6 0.8648194 4.591167 0.10 0.10 0.8648194+ 4.591167i
#> 7 0.9111431 5.254762 0.12 0.12 0.9111431+ 5.254762i
#> 8 0.9029517 5.745695 0.14 0.14 0.9029517+ 5.745695i
#> 9 0.8714107 6.300872 0.16 0.16 0.8714107+ 6.300872i
#> 10 0.8952942 6.995710 0.18 0.18 0.8952942+ 6.995710i
#> 11 1.0285338 7.554579 0.20 0.20 1.0285338+ 7.554579i
#> 12 0.9953501 8.129223 0.22 0.22 0.9953501+ 8.129223i
#> 13 1.0727463 8.738312 0.24 0.24 1.0727463+ 8.738312i
#> 14 1.2666258 9.327241 0.26 0.26 1.2666258+ 9.327241i
#> 15 1.3506619 9.938040 0.28 0.28 1.3506619+ 9.938040i
#> 16 1.4077739 10.523108 0.30 0.30 1.4077739+10.523108i
#> 17 1.5125240 11.050717 0.32 0.32 1.5125240+11.050717i
#> 18 1.6193187 11.664790 0.34 0.34 1.6193187+11.664790i
#> 19 1.9054832 12.495657 0.36 0.36 1.9054832+12.495657i
#> 20 1.9177951 13.137350 0.38 0.38 1.9177951+13.137350i
#> 21 1.9900420 13.602354 0.40 0.40 1.9900420+13.602354i
#> 22 1.9793020 14.279896 0.42 0.42 1.9793020+14.279896i
#> 23 2.1097681 14.743182 0.44 0.44 2.1097681+14.743182i
#> 24 2.1368724 15.381232 0.46 0.46 2.1368724+15.381232i
#> displacement Trajectory Simulation TrajSim
#> 1 0.000000000+0.0000000i Traj_2 Sim_7 TrajSim_2_7
#> 2 0.081482978+0.4649052i Traj_2 Sim_7 TrajSim_2_7
#> 3 0.116533030+0.6971389i Traj_2 Sim_7 TrajSim_2_7
#> 4 0.181678288+0.7453689i Traj_2 Sim_7 TrajSim_2_7
#> 5 0.076634522+0.6025941i Traj_2 Sim_7 TrajSim_2_7
#> 6 0.072490626+0.5211596i Traj_2 Sim_7 TrajSim_2_7
#> 7 0.046323644+0.6635955i Traj_2 Sim_7 TrajSim_2_7
#> 8 -0.008191409+0.4909326i Traj_2 Sim_7 TrajSim_2_7
#> 9 -0.031540950+0.5551770i Traj_2 Sim_7 TrajSim_2_7
#> 10 0.023883465+0.6948379i Traj_2 Sim_7 TrajSim_2_7
#> 11 0.133239643+0.5588688i Traj_2 Sim_7 TrajSim_2_7
#> 12 -0.033183686+0.5746439i Traj_2 Sim_7 TrajSim_2_7
#> 13 0.077396130+0.6090900i Traj_2 Sim_7 TrajSim_2_7
#> 14 0.193879539+0.5889287i Traj_2 Sim_7 TrajSim_2_7
#> 15 0.084036128+0.6107986i Traj_2 Sim_7 TrajSim_2_7
#> 16 0.057111992+0.5850684i Traj_2 Sim_7 TrajSim_2_7
#> 17 0.104750048+0.5276085i Traj_2 Sim_7 TrajSim_2_7
#> 18 0.106794740+0.6140732i Traj_2 Sim_7 TrajSim_2_7
#> 19 0.286164522+0.8308670i Traj_2 Sim_7 TrajSim_2_7
#> 20 0.012311822+0.6416928i Traj_2 Sim_7 TrajSim_2_7
#> 21 0.072246930+0.4650046i Traj_2 Sim_7 TrajSim_2_7
#> 22 -0.010739970+0.6775418i Traj_2 Sim_7 TrajSim_2_7
#> 23 0.130466113+0.4632860i Traj_2 Sim_7 TrajSim_2_7
#> 24 0.027104219+0.6380499i Traj_2 Sim_7 TrajSim_2_7
#>
#>
#> [[8]]
#> [[8]][[1]]
#> x y time displacementTime polar
#> 1 0.6960000 0.946000 0.00 0.00 0.6960000+ 0.946000i
#> 2 0.6227046 1.489653 0.02 0.02 0.6227046+ 1.489653i
#> 3 0.5324501 2.002940 0.04 0.04 0.5324501+ 2.002940i
#> 4 0.6947851 2.521594 0.06 0.06 0.6947851+ 2.521594i
#> 5 0.6909771 3.002200 0.08 0.08 0.6909771+ 3.002200i
#> 6 0.6699848 3.560218 0.10 0.10 0.6699848+ 3.560218i
#> 7 0.7767468 4.028440 0.12 0.12 0.7767468+ 4.028440i
#> 8 0.8571002 4.565840 0.14 0.14 0.8571002+ 4.565840i
#> 9 0.9088469 4.973058 0.16 0.16 0.9088469+ 4.973058i
#> 10 0.8323844 5.520223 0.18 0.18 0.8323844+ 5.520223i
#> 11 0.8550841 6.152396 0.20 0.20 0.8550841+ 6.152396i
#> 12 0.9516193 6.733114 0.22 0.22 0.9516193+ 6.733114i
#> 13 0.9091055 7.328601 0.24 0.24 0.9091055+ 7.328601i
#> 14 1.0334796 7.883843 0.26 0.26 1.0334796+ 7.883843i
#> 15 1.0414474 8.408078 0.28 0.28 1.0414474+ 8.408078i
#> 16 1.1211536 8.925632 0.30 0.30 1.1211536+ 8.925632i
#> 17 1.1316923 9.360083 0.32 0.32 1.1316923+ 9.360083i
#> 18 1.2282334 9.878329 0.34 0.34 1.2282334+ 9.878329i
#> 19 1.3483885 10.419823 0.36 0.36 1.3483885+10.419823i
#> 20 1.3785136 10.982863 0.38 0.38 1.3785136+10.982863i
#> 21 1.3067693 11.485408 0.40 0.40 1.3067693+11.485408i
#> 22 1.2279728 12.132442 0.42 0.42 1.2279728+12.132442i
#> 23 1.2859302 12.651842 0.44 0.44 1.2859302+12.651842i
#> 24 1.2317703 13.237454 0.46 0.46 1.2317703+13.237454i
#> 25 1.2115073 13.729296 0.48 0.48 1.2115073+13.729296i
#> 26 1.3156362 14.275507 0.50 0.50 1.3156362+14.275507i
#> 27 1.3487476 14.839698 0.52 0.52 1.3487476+14.839698i
#> 28 1.4585717 15.338276 0.54 0.54 1.4585717+15.338276i
#> 29 1.6582245 15.868451 0.56 0.56 1.6582245+15.868451i
#> displacement Trajectory Simulation TrajSim
#> 1 0.000000000+0.0000000i Traj_1 Sim_8 TrajSim_1_8
#> 2 -0.073295365+0.5436531i Traj_1 Sim_8 TrajSim_1_8
#> 3 -0.090254572+0.5132864i Traj_1 Sim_8 TrajSim_1_8
#> 4 0.162335086+0.5186549i Traj_1 Sim_8 TrajSim_1_8
#> 5 -0.003808035+0.4806051i Traj_1 Sim_8 TrajSim_1_8
#> 6 -0.020992268+0.5580185i Traj_1 Sim_8 TrajSim_1_8
#> 7 0.106761982+0.4682217i Traj_1 Sim_8 TrajSim_1_8
#> 8 0.080353404+0.5374002i Traj_1 Sim_8 TrajSim_1_8
#> 9 0.051746654+0.4072182i Traj_1 Sim_8 TrajSim_1_8
#> 10 -0.076462436+0.5471646i Traj_1 Sim_8 TrajSim_1_8
#> 11 0.022699655+0.6321729i Traj_1 Sim_8 TrajSim_1_8
#> 12 0.096535147+0.5807178i Traj_1 Sim_8 TrajSim_1_8
#> 13 -0.042513734+0.5954878i Traj_1 Sim_8 TrajSim_1_8
#> 14 0.124374058+0.5552418i Traj_1 Sim_8 TrajSim_1_8
#> 15 0.007967855+0.5242350i Traj_1 Sim_8 TrajSim_1_8
#> 16 0.079706192+0.5175533i Traj_1 Sim_8 TrajSim_1_8
#> 17 0.010538705+0.4344510i Traj_1 Sim_8 TrajSim_1_8
#> 18 0.096541083+0.5182462i Traj_1 Sim_8 TrajSim_1_8
#> 19 0.120155118+0.5414946i Traj_1 Sim_8 TrajSim_1_8
#> 20 0.030125081+0.5630401i Traj_1 Sim_8 TrajSim_1_8
#> 21 -0.071744326+0.5025448i Traj_1 Sim_8 TrajSim_1_8
#> 22 -0.078796463+0.6470339i Traj_1 Sim_8 TrajSim_1_8
#> 23 0.057957348+0.5194003i Traj_1 Sim_8 TrajSim_1_8
#> 24 -0.054159833+0.5856111i Traj_1 Sim_8 TrajSim_1_8
#> 25 -0.020263029+0.4918423i Traj_1 Sim_8 TrajSim_1_8
#> 26 0.104128866+0.5462117i Traj_1 Sim_8 TrajSim_1_8
#> 27 0.033111379+0.5641907i Traj_1 Sim_8 TrajSim_1_8
#> 28 0.109824187+0.4985779i Traj_1 Sim_8 TrajSim_1_8
#> 29 0.199652784+0.5301750i Traj_1 Sim_8 TrajSim_1_8
#>
#> [[8]][[2]]
#> x y time displacementTime polar
#> 1 0.3360000 1.560000 0.00 0.00 0.3360000+ 1.560000i
#> 2 0.3936292 2.171527 0.02 0.02 0.3936292+ 2.171527i
#> 3 0.6229374 2.784189 0.04 0.04 0.6229374+ 2.784189i
#> 4 0.7656598 3.359866 0.06 0.06 0.7656598+ 3.359866i
#> 5 0.8418173 3.876140 0.08 0.08 0.8418173+ 3.876140i
#> 6 0.9825336 4.478381 0.10 0.10 0.9825336+ 4.478381i
#> 7 1.0577384 5.108092 0.12 0.12 1.0577384+ 5.108092i
#> 8 0.9484957 5.685533 0.14 0.14 0.9484957+ 5.685533i
#> 9 0.9768354 6.227205 0.16 0.16 0.9768354+ 6.227205i
#> 10 1.1444140 6.788606 0.18 0.18 1.1444140+ 6.788606i
#> 11 1.1525204 7.415814 0.20 0.20 1.1525204+ 7.415814i
#> 12 1.2201693 7.870526 0.22 0.22 1.2201693+ 7.870526i
#> 13 1.4436033 8.456689 0.24 0.24 1.4436033+ 8.456689i
#> 14 1.6562679 9.131091 0.26 0.26 1.6562679+ 9.131091i
#> 15 1.7511848 9.751649 0.28 0.28 1.7511848+ 9.751649i
#> 16 1.7108411 10.423744 0.30 0.30 1.7108411+10.423744i
#> 17 1.7768178 10.937939 0.32 0.32 1.7768178+10.937939i
#> 18 1.8934477 11.522937 0.34 0.34 1.8934477+11.522937i
#> 19 2.0769499 12.103520 0.36 0.36 2.0769499+12.103520i
#> 20 2.1633659 12.721520 0.38 0.38 2.1633659+12.721520i
#> 21 2.2060358 13.338562 0.40 0.40 2.2060358+13.338562i
#> 22 2.2950680 14.028682 0.42 0.42 2.2950680+14.028682i
#> 23 2.3531148 14.596060 0.44 0.44 2.3531148+14.596060i
#> 24 2.3078183 15.201024 0.46 0.46 2.3078183+15.201024i
#> displacement Trajectory Simulation TrajSim
#> 1 0.000000000+0.0000000i Traj_2 Sim_8 TrajSim_2_8
#> 2 0.057629169+0.6115267i Traj_2 Sim_8 TrajSim_2_8
#> 3 0.229308211+0.6126626i Traj_2 Sim_8 TrajSim_2_8
#> 4 0.142722442+0.5756763i Traj_2 Sim_8 TrajSim_2_8
#> 5 0.076157482+0.5162746i Traj_2 Sim_8 TrajSim_2_8
#> 6 0.140716258+0.6022408i Traj_2 Sim_8 TrajSim_2_8
#> 7 0.075204808+0.6297105i Traj_2 Sim_8 TrajSim_2_8
#> 8 -0.109242654+0.5774412i Traj_2 Sim_8 TrajSim_2_8
#> 9 0.028339656+0.5416726i Traj_2 Sim_8 TrajSim_2_8
#> 10 0.167578604+0.5614004i Traj_2 Sim_8 TrajSim_2_8
#> 11 0.008106393+0.6272086i Traj_2 Sim_8 TrajSim_2_8
#> 12 0.067648953+0.4547118i Traj_2 Sim_8 TrajSim_2_8
#> 13 0.223434027+0.5861625i Traj_2 Sim_8 TrajSim_2_8
#> 14 0.212664502+0.6744029i Traj_2 Sim_8 TrajSim_2_8
#> 15 0.094916972+0.6205571i Traj_2 Sim_8 TrajSim_2_8
#> 16 -0.040343685+0.6720950i Traj_2 Sim_8 TrajSim_2_8
#> 17 0.065976670+0.5141952i Traj_2 Sim_8 TrajSim_2_8
#> 18 0.116629848+0.5849978i Traj_2 Sim_8 TrajSim_2_8
#> 19 0.183502273+0.5805831i Traj_2 Sim_8 TrajSim_2_8
#> 20 0.086415959+0.6180008i Traj_2 Sim_8 TrajSim_2_8
#> 21 0.042669903+0.6170416i Traj_2 Sim_8 TrajSim_2_8
#> 22 0.089032176+0.6901197i Traj_2 Sim_8 TrajSim_2_8
#> 23 0.058046809+0.5673780i Traj_2 Sim_8 TrajSim_2_8
#> 24 -0.045296500+0.6049642i Traj_2 Sim_8 TrajSim_2_8
#>
#>
#> [[9]]
#> [[9]][[1]]
#> x y time displacementTime polar
#> 1 0.6960000 0.946000 0.00 0.00 0.6960000+ 0.946000i
#> 2 0.6581449 1.525979 0.02 0.02 0.6581449+ 1.525979i
#> 3 0.7705667 2.086359 0.04 0.04 0.7705667+ 2.086359i
#> 4 0.9433232 2.585746 0.06 0.06 0.9433232+ 2.585746i
#> 5 1.1318653 3.019102 0.08 0.08 1.1318653+ 3.019102i
#> 6 1.1337527 3.542746 0.10 0.10 1.1337527+ 3.542746i
#> 7 1.0505803 4.077615 0.12 0.12 1.0505803+ 4.077615i
#> 8 1.0151479 4.661243 0.14 0.14 1.0151479+ 4.661243i
#> 9 0.9282032 5.104392 0.16 0.16 0.9282032+ 5.104392i
#> 10 1.0233102 5.636710 0.18 0.18 1.0233102+ 5.636710i
#> 11 0.9941240 6.186774 0.20 0.20 0.9941240+ 6.186774i
#> 12 1.1311208 6.853057 0.22 0.22 1.1311208+ 6.853057i
#> 13 1.1482710 7.475459 0.24 0.24 1.1482710+ 7.475459i
#> 14 1.3126473 7.993892 0.26 0.26 1.3126473+ 7.993892i
#> 15 1.4146500 8.571816 0.28 0.28 1.4146500+ 8.571816i
#> 16 1.5901901 9.096728 0.30 0.30 1.5901901+ 9.096728i
#> 17 1.4729830 9.663750 0.32 0.32 1.4729830+ 9.663750i
#> 18 1.4912966 10.154633 0.34 0.34 1.4912966+10.154633i
#> 19 1.4492141 10.669618 0.36 0.36 1.4492141+10.669618i
#> 20 1.5379622 11.195148 0.38 0.38 1.5379622+11.195148i
#> 21 1.6065049 11.737427 0.40 0.40 1.6065049+11.737427i
#> 22 1.7026277 12.277434 0.42 0.42 1.7026277+12.277434i
#> 23 1.8097541 12.824945 0.44 0.44 1.8097541+12.824945i
#> 24 1.8575310 13.414073 0.46 0.46 1.8575310+13.414073i
#> 25 1.7961435 13.944100 0.48 0.48 1.7961435+13.944100i
#> 26 1.7830808 14.543459 0.50 0.50 1.7830808+14.543459i
#> 27 1.7303293 15.045348 0.52 0.52 1.7303293+15.045348i
#> 28 1.9366225 15.566196 0.54 0.54 1.9366225+15.566196i
#> 29 2.1129365 15.992642 0.56 0.56 2.1129365+15.992642i
#> displacement Trajectory Simulation TrajSim
#> 1 0.000000000+0.0000000i Traj_1 Sim_9 TrajSim_1_9
#> 2 -0.037855135+0.5799792i Traj_1 Sim_9 TrajSim_1_9
#> 3 0.112421880+0.5603799i Traj_1 Sim_9 TrajSim_1_9
#> 4 0.172756408+0.4993872i Traj_1 Sim_9 TrajSim_1_9
#> 5 0.188542133+0.4333553i Traj_1 Sim_9 TrajSim_1_9
#> 6 0.001887368+0.5236441i Traj_1 Sim_9 TrajSim_1_9
#> 7 -0.083172320+0.5348692i Traj_1 Sim_9 TrajSim_1_9
#> 8 -0.035432417+0.5836283i Traj_1 Sim_9 TrajSim_1_9
#> 9 -0.086944673+0.4431483i Traj_1 Sim_9 TrajSim_1_9
#> 10 0.095106934+0.5323189i Traj_1 Sim_9 TrajSim_1_9
#> 11 -0.029186199+0.5500631i Traj_1 Sim_9 TrajSim_1_9
#> 12 0.136996805+0.6662834i Traj_1 Sim_9 TrajSim_1_9
#> 13 0.017150194+0.6224018i Traj_1 Sim_9 TrajSim_1_9
#> 14 0.164376367+0.5184330i Traj_1 Sim_9 TrajSim_1_9
#> 15 0.102002697+0.5779242i Traj_1 Sim_9 TrajSim_1_9
#> 16 0.175540074+0.5249117i Traj_1 Sim_9 TrajSim_1_9
#> 17 -0.117207129+0.5670223i Traj_1 Sim_9 TrajSim_1_9
#> 18 0.018313607+0.4908829i Traj_1 Sim_9 TrajSim_1_9
#> 19 -0.042082507+0.5149849i Traj_1 Sim_9 TrajSim_1_9
#> 20 0.088748082+0.5255301i Traj_1 Sim_9 TrajSim_1_9
#> 21 0.068542696+0.5422788i Traj_1 Sim_9 TrajSim_1_9
#> 22 0.096122786+0.5400075i Traj_1 Sim_9 TrajSim_1_9
#> 23 0.107126448+0.5475107i Traj_1 Sim_9 TrajSim_1_9
#> 24 0.047776892+0.5891284i Traj_1 Sim_9 TrajSim_1_9
#> 25 -0.061387522+0.5300270i Traj_1 Sim_9 TrajSim_1_9
#> 26 -0.013062629+0.5993588i Traj_1 Sim_9 TrajSim_1_9
#> 27 -0.052751575+0.5018885i Traj_1 Sim_9 TrajSim_1_9
#> 28 0.206293215+0.5208484i Traj_1 Sim_9 TrajSim_1_9
#> 29 0.176314024+0.4264463i Traj_1 Sim_9 TrajSim_1_9
#>
#> [[9]][[2]]
#> x y time displacementTime polar
#> 1 0.3360000 1.560000 0.00 0.00 0.3360000+ 1.560000i
#> 2 0.2787543 2.093032 0.02 0.02 0.2787543+ 2.093032i
#> 3 0.2421954 2.699213 0.04 0.04 0.2421954+ 2.699213i
#> 4 0.2685557 3.372653 0.06 0.06 0.2685557+ 3.372653i
#> 5 0.4620105 3.890497 0.08 0.08 0.4620105+ 3.890497i
#> 6 0.5925586 4.422727 0.10 0.10 0.5925586+ 4.422727i
#> 7 0.7541798 5.108568 0.12 0.12 0.7541798+ 5.108568i
#> 8 0.6675923 5.948347 0.14 0.14 0.6675923+ 5.948347i
#> 9 0.6707678 6.689203 0.16 0.16 0.6707678+ 6.689203i
#> 10 0.6875543 7.283251 0.18 0.18 0.6875543+ 7.283251i
#> 11 0.7811198 7.891470 0.20 0.20 0.7811198+ 7.891470i
#> 12 0.8416485 8.553656 0.22 0.22 0.8416485+ 8.553656i
#> 13 0.9434760 9.167473 0.24 0.24 0.9434760+ 9.167473i
#> 14 1.0724048 9.866832 0.26 0.26 1.0724048+ 9.866832i
#> 15 1.1538987 10.491243 0.28 0.28 1.1538987+10.491243i
#> 16 1.1777442 11.188339 0.30 0.30 1.1777442+11.188339i
#> 17 1.2660602 11.759878 0.32 0.32 1.2660602+11.759878i
#> 18 1.4083939 12.332271 0.34 0.34 1.4083939+12.332271i
#> 19 1.5382575 12.958581 0.36 0.36 1.5382575+12.958581i
#> 20 1.4674183 13.537889 0.38 0.38 1.4674183+13.537889i
#> 21 1.4901052 14.122743 0.40 0.40 1.4901052+14.122743i
#> 22 1.5396626 14.672896 0.42 0.42 1.5396626+14.672896i
#> 23 1.5550662 15.217562 0.44 0.44 1.5550662+15.217562i
#> 24 1.5605436 15.913839 0.46 0.46 1.5605436+15.913839i
#> displacement Trajectory Simulation TrajSim
#> 1 0.000000000+0.0000000i Traj_2 Sim_9 TrajSim_2_9
#> 2 -0.057245716+0.5330316i Traj_2 Sim_9 TrajSim_2_9
#> 3 -0.036558884+0.6061814i Traj_2 Sim_9 TrajSim_2_9
#> 4 0.026360283+0.6734395i Traj_2 Sim_9 TrajSim_2_9
#> 5 0.193454796+0.5178442i Traj_2 Sim_9 TrajSim_2_9
#> 6 0.130548095+0.5322302i Traj_2 Sim_9 TrajSim_2_9
#> 7 0.161621203+0.6858409i Traj_2 Sim_9 TrajSim_2_9
#> 8 -0.086587452+0.8397787i Traj_2 Sim_9 TrajSim_2_9
#> 9 0.003175447+0.7408559i Traj_2 Sim_9 TrajSim_2_9
#> 10 0.016786507+0.5940485i Traj_2 Sim_9 TrajSim_2_9
#> 11 0.093565526+0.6082186i Traj_2 Sim_9 TrajSim_2_9
#> 12 0.060528721+0.6621860i Traj_2 Sim_9 TrajSim_2_9
#> 13 0.101827508+0.6138169i Traj_2 Sim_9 TrajSim_2_9
#> 14 0.128928747+0.6993592i Traj_2 Sim_9 TrajSim_2_9
#> 15 0.081493889+0.6244115i Traj_2 Sim_9 TrajSim_2_9
#> 16 0.023845510+0.6970961i Traj_2 Sim_9 TrajSim_2_9
#> 17 0.088316012+0.5715385i Traj_2 Sim_9 TrajSim_2_9
#> 18 0.142333734+0.5723928i Traj_2 Sim_9 TrajSim_2_9
#> 19 0.129863541+0.6263105i Traj_2 Sim_9 TrajSim_2_9
#> 20 -0.070839144+0.5793076i Traj_2 Sim_9 TrajSim_2_9
#> 21 0.022686839+0.5848544i Traj_2 Sim_9 TrajSim_2_9
#> 22 0.049557418+0.5501528i Traj_2 Sim_9 TrajSim_2_9
#> 23 0.015403627+0.5446665i Traj_2 Sim_9 TrajSim_2_9
#> 24 0.005477418+0.6962762i Traj_2 Sim_9 TrajSim_2_9
#>
#>
#> [[10]]
#> [[10]][[1]]
#> x y time displacementTime polar
#> 1 0.6960000 0.946000 0.00 0.00 0.6960000+ 0.946000i
#> 2 0.7687393 1.403172 0.02 0.02 0.7687393+ 1.403172i
#> 3 0.8512869 1.887325 0.04 0.04 0.8512869+ 1.887325i
#> 4 0.7368751 2.354411 0.06 0.06 0.7368751+ 2.354411i
#> 5 0.8245658 2.848540 0.08 0.08 0.8245658+ 2.848540i
#> 6 0.7527782 3.415633 0.10 0.10 0.7527782+ 3.415633i
#> 7 0.8777779 3.911872 0.12 0.12 0.8777779+ 3.911872i
#> 8 0.8750472 4.339195 0.14 0.14 0.8750472+ 4.339195i
#> 9 1.0627317 4.900868 0.16 0.16 1.0627317+ 4.900868i
#> 10 1.0969922 5.435257 0.18 0.18 1.0969922+ 5.435257i
#> 11 1.1077407 6.084828 0.20 0.20 1.1077407+ 6.084828i
#> 12 1.1563303 6.646063 0.22 0.22 1.1563303+ 6.646063i
#> 13 1.1899232 7.160909 0.24 0.24 1.1899232+ 7.160909i
#> 14 1.3229681 7.630724 0.26 0.26 1.3229681+ 7.630724i
#> 15 1.3769778 8.175163 0.28 0.28 1.3769778+ 8.175163i
#> 16 1.4089192 8.688804 0.30 0.30 1.4089192+ 8.688804i
#> 17 1.5581506 9.319870 0.32 0.32 1.5581506+ 9.319870i
#> 18 1.6333103 9.853186 0.34 0.34 1.6333103+ 9.853186i
#> 19 1.6689649 10.268655 0.36 0.36 1.6689649+10.268655i
#> 20 1.7072067 10.739525 0.38 0.38 1.7072067+10.739525i
#> 21 1.8557170 11.224437 0.40 0.40 1.8557170+11.224437i
#> 22 2.0218462 11.671943 0.42 0.42 2.0218462+11.671943i
#> 23 2.1624831 12.156125 0.44 0.44 2.1624831+12.156125i
#> 24 2.2469182 12.713039 0.46 0.46 2.2469182+12.713039i
#> 25 2.4241155 13.153032 0.48 0.48 2.4241155+13.153032i
#> 26 2.5858392 13.699011 0.50 0.50 2.5858392+13.699011i
#> 27 2.6845748 14.304975 0.52 0.52 2.6845748+14.304975i
#> 28 2.7524948 14.775906 0.54 0.54 2.7524948+14.775906i
#> 29 2.8450737 15.306706 0.56 0.56 2.8450737+15.306706i
#> displacement Trajectory Simulation TrajSim
#> 1 0.000000000+0.0000000i Traj_1 Sim_10 TrajSim_1_10
#> 2 0.072739295+0.4571721i Traj_1 Sim_10 TrajSim_1_10
#> 3 0.082547612+0.4841529i Traj_1 Sim_10 TrajSim_1_10
#> 4 -0.114411758+0.4670861i Traj_1 Sim_10 TrajSim_1_10
#> 5 0.087690690+0.4941287i Traj_1 Sim_10 TrajSim_1_10
#> 6 -0.071787610+0.5670933i Traj_1 Sim_10 TrajSim_1_10
#> 7 0.124999686+0.4962390i Traj_1 Sim_10 TrajSim_1_10
#> 8 -0.002730709+0.4273235i Traj_1 Sim_10 TrajSim_1_10
#> 9 0.187684492+0.5616726i Traj_1 Sim_10 TrajSim_1_10
#> 10 0.034260526+0.5343890i Traj_1 Sim_10 TrajSim_1_10
#> 11 0.010748496+0.6495704i Traj_1 Sim_10 TrajSim_1_10
#> 12 0.048589557+0.5612350i Traj_1 Sim_10 TrajSim_1_10
#> 13 0.033592963+0.5148464i Traj_1 Sim_10 TrajSim_1_10
#> 14 0.133044871+0.4698152i Traj_1 Sim_10 TrajSim_1_10
#> 15 0.054009690+0.5444384i Traj_1 Sim_10 TrajSim_1_10
#> 16 0.031941425+0.5136417i Traj_1 Sim_10 TrajSim_1_10
#> 17 0.149231333+0.6310661i Traj_1 Sim_10 TrajSim_1_10
#> 18 0.075159742+0.5333160i Traj_1 Sim_10 TrajSim_1_10
#> 19 0.035654642+0.4154685i Traj_1 Sim_10 TrajSim_1_10
#> 20 0.038241760+0.4708699i Traj_1 Sim_10 TrajSim_1_10
#> 21 0.148510251+0.4849123i Traj_1 Sim_10 TrajSim_1_10
#> 22 0.166129221+0.4475064i Traj_1 Sim_10 TrajSim_1_10
#> 23 0.140636941+0.4841818i Traj_1 Sim_10 TrajSim_1_10
#> 24 0.084435108+0.5569137i Traj_1 Sim_10 TrajSim_1_10
#> 25 0.177197281+0.4399928i Traj_1 Sim_10 TrajSim_1_10
#> 26 0.161723705+0.5459794i Traj_1 Sim_10 TrajSim_1_10
#> 27 0.098735548+0.6059638i Traj_1 Sim_10 TrajSim_1_10
#> 28 0.067920015+0.4709310i Traj_1 Sim_10 TrajSim_1_10
#> 29 0.092578941+0.5308003i Traj_1 Sim_10 TrajSim_1_10
#>
#> [[10]][[2]]
#> x y time displacementTime polar
#> 1 0.3360000 1.560000 0.00 0.00 0.3360000+ 1.560000i
#> 2 0.4814144 2.059857 0.02 0.02 0.4814144+ 2.059857i
#> 3 0.5411629 2.743453 0.04 0.04 0.5411629+ 2.743453i
#> 4 0.6766983 3.424697 0.06 0.06 0.6766983+ 3.424697i
#> 5 0.6755556 4.048676 0.08 0.08 0.6755556+ 4.048676i
#> 6 0.7629699 4.586653 0.10 0.10 0.7629699+ 4.586653i
#> 7 0.7962770 5.145277 0.12 0.12 0.7962770+ 5.145277i
#> 8 1.0256207 5.748047 0.14 0.14 1.0256207+ 5.748047i
#> 9 1.1063469 6.375689 0.16 0.16 1.1063469+ 6.375689i
#> 10 1.1699532 7.056329 0.18 0.18 1.1699532+ 7.056329i
#> 11 1.2215055 7.715938 0.20 0.20 1.2215055+ 7.715938i
#> 12 1.4020896 8.376618 0.22 0.22 1.4020896+ 8.376618i
#> 13 1.5671265 8.968049 0.24 0.24 1.5671265+ 8.968049i
#> 14 1.6378287 9.576641 0.26 0.26 1.6378287+ 9.576641i
#> 15 1.6547840 10.126282 0.28 0.28 1.6547840+10.126282i
#> 16 1.7691978 10.870586 0.30 0.30 1.7691978+10.870586i
#> 17 1.9062978 11.535937 0.32 0.32 1.9062978+11.535937i
#> 18 1.8473967 12.142278 0.34 0.34 1.8473967+12.142278i
#> 19 1.8921217 12.787620 0.36 0.36 1.8921217+12.787620i
#> 20 1.9594321 13.367038 0.38 0.38 1.9594321+13.367038i
#> 21 2.0583780 13.892744 0.40 0.40 2.0583780+13.892744i
#> 22 2.0773319 14.510795 0.42 0.42 2.0773319+14.510795i
#> 23 2.0871684 15.031755 0.44 0.44 2.0871684+15.031755i
#> 24 2.3615210 15.616074 0.46 0.46 2.3615210+15.616074i
#> displacement Trajectory Simulation TrajSim
#> 1 0.000000000+0.0000000i Traj_2 Sim_10 TrajSim_2_10
#> 2 0.145414373+0.4998566i Traj_2 Sim_10 TrajSim_2_10
#> 3 0.059748511+0.6835968i Traj_2 Sim_10 TrajSim_2_10
#> 4 0.135535386+0.6812435i Traj_2 Sim_10 TrajSim_2_10
#> 5 -0.001142680+0.6239796i Traj_2 Sim_10 TrajSim_2_10
#> 6 0.087414355+0.5379762i Traj_2 Sim_10 TrajSim_2_10
#> 7 0.033307040+0.5586248i Traj_2 Sim_10 TrajSim_2_10
#> 8 0.229343756+0.6027696i Traj_2 Sim_10 TrajSim_2_10
#> 9 0.080726177+0.6276422i Traj_2 Sim_10 TrajSim_2_10
#> 10 0.063606241+0.6806402i Traj_2 Sim_10 TrajSim_2_10
#> 11 0.051552320+0.6596089i Traj_2 Sim_10 TrajSim_2_10
#> 12 0.180584106+0.6606797i Traj_2 Sim_10 TrajSim_2_10
#> 13 0.165036907+0.5914309i Traj_2 Sim_10 TrajSim_2_10
#> 14 0.070702215+0.6085924i Traj_2 Sim_10 TrajSim_2_10
#> 15 0.016955249+0.5496408i Traj_2 Sim_10 TrajSim_2_10
#> 16 0.114413841+0.7443040i Traj_2 Sim_10 TrajSim_2_10
#> 17 0.137100024+0.6653509i Traj_2 Sim_10 TrajSim_2_10
#> 18 -0.058901102+0.6063408i Traj_2 Sim_10 TrajSim_2_10
#> 19 0.044725009+0.6453425i Traj_2 Sim_10 TrajSim_2_10
#> 20 0.067310353+0.5794175i Traj_2 Sim_10 TrajSim_2_10
#> 21 0.098945948+0.5257063i Traj_2 Sim_10 TrajSim_2_10
#> 22 0.018953897+0.6180510i Traj_2 Sim_10 TrajSim_2_10
#> 23 0.009836446+0.5209598i Traj_2 Sim_10 TrajSim_2_10
#> 24 0.274352639+0.5843188i Traj_2 Sim_10 TrajSim_2_10
sim_constrained_paluxy <- simulate_track(PaluxyRiver, nsim = 100, model = "Constrained")
print(sim_constrained_paluxy[1:10])#> [[1]]
#> [[1]][[1]]
#> x y time displacementTime polar
#> 1 0.696000000 0.946000 0.00 0.00 0.696000000+ 0.946000i
#> 2 0.752330596 1.423733 0.02 0.02 0.752330596+ 1.423733i
#> 3 0.770343613 2.047671 0.04 0.04 0.770343613+ 2.047671i
#> 4 0.761695743 2.572368 0.06 0.06 0.761695743+ 2.572368i
#> 5 0.737755068 3.053608 0.08 0.08 0.737755068+ 3.053608i
#> 6 0.724968008 3.628582 0.10 0.10 0.724968008+ 3.628582i
#> 7 0.686518898 4.154617 0.12 0.12 0.686518898+ 4.154617i
#> 8 0.699195808 4.634407 0.14 0.14 0.699195808+ 4.634407i
#> 9 0.642250047 5.168512 0.16 0.16 0.642250047+ 5.168512i
#> 10 0.577323350 5.649652 0.18 0.18 0.577323350+ 5.649652i
#> 11 0.509082399 6.095985 0.20 0.20 0.509082399+ 6.095985i
#> 12 0.416571934 6.593295 0.22 0.22 0.416571934+ 6.593295i
#> 13 0.313507128 7.062312 0.24 0.24 0.313507128+ 7.062312i
#> 14 0.195224637 7.525802 0.26 0.26 0.195224637+ 7.525802i
#> 15 0.051866602 8.137048 0.28 0.28 0.051866602+ 8.137048i
#> 16 -0.006535188 8.586326 0.30 0.30 -0.006535188+ 8.586326i
#> 17 -0.037289836 9.115063 0.32 0.32 -0.037289836+ 9.115063i
#> 18 -0.069642616 9.689576 0.34 0.34 -0.069642616+ 9.689576i
#> 19 -0.091833510 10.164871 0.36 0.36 -0.091833510+10.164871i
#> 20 -0.151686413 10.656320 0.38 0.38 -0.151686413+10.656320i
#> 21 -0.270641962 11.187028 0.40 0.40 -0.270641962+11.187028i
#> 22 -0.365617552 11.767690 0.42 0.42 -0.365617552+11.767690i
#> 23 -0.396714815 12.241798 0.44 0.44 -0.396714815+12.241798i
#> 24 -0.425477422 12.716732 0.46 0.46 -0.425477422+12.716732i
#> 25 -0.452533325 13.265109 0.48 0.48 -0.452533325+13.265109i
#> 26 -0.522721674 13.925975 0.50 0.50 -0.522721674+13.925975i
#> 27 -0.579153770 14.408487 0.52 0.52 -0.579153770+14.408487i
#> 28 -0.701468478 14.999407 0.54 0.54 -0.701468478+14.999407i
#> 29 -0.757003247 15.468365 0.56 0.56 -0.757003247+15.468365i
#> displacement Trajectory Simulation TrajSim
#> 1 0.000000000+0.0000000i Traj_1 Sim_1 TrajSim_1_1
#> 2 0.056330596+0.4777332i Traj_1 Sim_1 TrajSim_1_1
#> 3 0.018013017+0.6239381i Traj_1 Sim_1 TrajSim_1_1
#> 4 -0.008647871+0.5246967i Traj_1 Sim_1 TrajSim_1_1
#> 5 -0.023940674+0.4812396i Traj_1 Sim_1 TrajSim_1_1
#> 6 -0.012787060+0.5749746i Traj_1 Sim_1 TrajSim_1_1
#> 7 -0.038449110+0.5260343i Traj_1 Sim_1 TrajSim_1_1
#> 8 0.012676910+0.4797901i Traj_1 Sim_1 TrajSim_1_1
#> 9 -0.056945760+0.5341058i Traj_1 Sim_1 TrajSim_1_1
#> 10 -0.064926697+0.4811392i Traj_1 Sim_1 TrajSim_1_1
#> 11 -0.068240951+0.4463331i Traj_1 Sim_1 TrajSim_1_1
#> 12 -0.092510465+0.4973098i Traj_1 Sim_1 TrajSim_1_1
#> 13 -0.103064806+0.4690175i Traj_1 Sim_1 TrajSim_1_1
#> 14 -0.118282491+0.4634902i Traj_1 Sim_1 TrajSim_1_1
#> 15 -0.143358035+0.6112461i Traj_1 Sim_1 TrajSim_1_1
#> 16 -0.058401789+0.4492772i Traj_1 Sim_1 TrajSim_1_1
#> 17 -0.030754648+0.5287368i Traj_1 Sim_1 TrajSim_1_1
#> 18 -0.032352780+0.5745131i Traj_1 Sim_1 TrajSim_1_1
#> 19 -0.022190894+0.4752957i Traj_1 Sim_1 TrajSim_1_1
#> 20 -0.059852903+0.4914490i Traj_1 Sim_1 TrajSim_1_1
#> 21 -0.118955549+0.5307073i Traj_1 Sim_1 TrajSim_1_1
#> 22 -0.094975590+0.5806624i Traj_1 Sim_1 TrajSim_1_1
#> 23 -0.031097263+0.4741081i Traj_1 Sim_1 TrajSim_1_1
#> 24 -0.028762607+0.4749335i Traj_1 Sim_1 TrajSim_1_1
#> 25 -0.027055904+0.5483778i Traj_1 Sim_1 TrajSim_1_1
#> 26 -0.070188349+0.6608650i Traj_1 Sim_1 TrajSim_1_1
#> 27 -0.056432096+0.4825125i Traj_1 Sim_1 TrajSim_1_1
#> 28 -0.122314707+0.5909199i Traj_1 Sim_1 TrajSim_1_1
#> 29 -0.055534769+0.4689583i Traj_1 Sim_1 TrajSim_1_1
#>
#> [[1]][[2]]
#> x y time displacementTime polar
#> 1 0.33600000 1.560000 0.00 0.00 0.33600000+ 1.560000i
#> 2 0.39049785 2.060381 0.02 0.02 0.39049785+ 2.060381i
#> 3 0.46261717 2.828618 0.04 0.04 0.46261717+ 2.828618i
#> 4 0.59424277 3.508399 0.06 0.06 0.59424277+ 3.508399i
#> 5 0.73077613 4.032805 0.08 0.08 0.73077613+ 4.032805i
#> 6 0.84890148 4.724455 0.10 0.10 0.84890148+ 4.724455i
#> 7 0.95690608 5.365669 0.12 0.12 0.95690608+ 5.365669i
#> 8 0.92368740 6.108208 0.14 0.14 0.92368740+ 6.108208i
#> 9 0.74262018 6.688030 0.16 0.16 0.74262018+ 6.688030i
#> 10 0.47321117 7.346083 0.18 0.18 0.47321117+ 7.346083i
#> 11 0.39514799 7.868975 0.20 0.20 0.39514799+ 7.868975i
#> 12 0.22761791 8.535409 0.22 0.22 0.22761791+ 8.535409i
#> 13 -0.04637412 9.149531 0.24 0.24 -0.04637412+ 9.149531i
#> 14 -0.31804541 9.737747 0.26 0.26 -0.31804541+ 9.737747i
#> 15 -0.61891435 10.234103 0.28 0.28 -0.61891435+10.234103i
#> 16 -0.85617900 10.864072 0.30 0.30 -0.85617900+10.864072i
#> 17 -1.19080613 11.308272 0.32 0.32 -1.19080613+11.308272i
#> 18 -1.49968464 11.828272 0.34 0.34 -1.49968464+11.828272i
#> 19 -1.94893190 12.492421 0.36 0.36 -1.94893190+12.492421i
#> 20 -2.34484686 13.129022 0.38 0.38 -2.34484686+13.129022i
#> 21 -2.81073851 13.676135 0.40 0.40 -2.81073851+13.676135i
#> 22 -3.22902594 14.091040 0.42 0.42 -3.22902594+14.091040i
#> 23 -3.57996248 14.491851 0.44 0.44 -3.57996248+14.491851i
#> 24 -3.94764778 14.978591 0.46 0.46 -3.94764778+14.978591i
#> displacement Trajectory Simulation TrajSim
#> 1 0.00000000+0.0000000i Traj_2 Sim_1 TrajSim_2_1
#> 2 0.05449785+0.5003806i Traj_2 Sim_1 TrajSim_2_1
#> 3 0.07211931+0.7682374i Traj_2 Sim_1 TrajSim_2_1
#> 4 0.13162560+0.6797813i Traj_2 Sim_1 TrajSim_2_1
#> 5 0.13653336+0.5244056i Traj_2 Sim_1 TrajSim_2_1
#> 6 0.11812535+0.6916498i Traj_2 Sim_1 TrajSim_2_1
#> 7 0.10800460+0.6412139i Traj_2 Sim_1 TrajSim_2_1
#> 8 -0.03321868+0.7425390i Traj_2 Sim_1 TrajSim_2_1
#> 9 -0.18106722+0.5798221i Traj_2 Sim_1 TrajSim_2_1
#> 10 -0.26940901+0.6580533i Traj_2 Sim_1 TrajSim_2_1
#> 11 -0.07806318+0.5228914i Traj_2 Sim_1 TrajSim_2_1
#> 12 -0.16753008+0.6664340i Traj_2 Sim_1 TrajSim_2_1
#> 13 -0.27399203+0.6141221i Traj_2 Sim_1 TrajSim_2_1
#> 14 -0.27167129+0.5882168i Traj_2 Sim_1 TrajSim_2_1
#> 15 -0.30086894+0.4963554i Traj_2 Sim_1 TrajSim_2_1
#> 16 -0.23726465+0.6299690i Traj_2 Sim_1 TrajSim_2_1
#> 17 -0.33462713+0.4441999i Traj_2 Sim_1 TrajSim_2_1
#> 18 -0.30887850+0.5199999i Traj_2 Sim_1 TrajSim_2_1
#> 19 -0.44924727+0.6641494i Traj_2 Sim_1 TrajSim_2_1
#> 20 -0.39591495+0.6366011i Traj_2 Sim_1 TrajSim_2_1
#> 21 -0.46589165+0.5471128i Traj_2 Sim_1 TrajSim_2_1
#> 22 -0.41828742+0.4149055i Traj_2 Sim_1 TrajSim_2_1
#> 23 -0.35093654+0.4008103i Traj_2 Sim_1 TrajSim_2_1
#> 24 -0.36768530+0.4867400i Traj_2 Sim_1 TrajSim_2_1
#>
#>
#> [[2]]
#> [[2]][[1]]
#> x y time displacementTime polar
#> 1 0.6960000 0.946000 0.00 0.00 0.6960000+ 0.946000i
#> 2 0.7239689 1.514434 0.02 0.02 0.7239689+ 1.514434i
#> 3 0.7553124 2.062140 0.04 0.04 0.7553124+ 2.062140i
#> 4 0.8194957 2.552110 0.06 0.06 0.8194957+ 2.552110i
#> 5 0.9023796 3.072341 0.08 0.08 0.9023796+ 3.072341i
#> 6 0.9279031 3.621776 0.10 0.10 0.9279031+ 3.621776i
#> 7 0.9862675 4.265805 0.12 0.12 0.9862675+ 4.265805i
#> 8 1.0101863 4.811921 0.14 0.14 1.0101863+ 4.811921i
#> 9 0.9631643 5.323129 0.16 0.16 0.9631643+ 5.323129i
#> 10 1.0047241 5.874902 0.18 0.18 1.0047241+ 5.874902i
#> 11 1.0322002 6.413431 0.20 0.20 1.0322002+ 6.413431i
#> 12 1.0592039 6.937921 0.22 0.22 1.0592039+ 6.937921i
#> 13 1.0839992 7.360645 0.24 0.24 1.0839992+ 7.360645i
#> 14 1.1547222 7.892033 0.26 0.26 1.1547222+ 7.892033i
#> 15 1.2041511 8.449614 0.28 0.28 1.2041511+ 8.449614i
#> 16 1.2521974 9.002191 0.30 0.30 1.2521974+ 9.002191i
#> 17 1.2968559 9.417702 0.32 0.32 1.2968559+ 9.417702i
#> 18 1.3219890 9.982362 0.34 0.34 1.3219890+ 9.982362i
#> 19 1.3303695 10.416658 0.36 0.36 1.3303695+10.416658i
#> 20 1.3797999 10.937964 0.38 0.38 1.3797999+10.937964i
#> 21 1.4617305 11.464167 0.40 0.40 1.4617305+11.464167i
#> 22 1.4924766 11.997571 0.42 0.42 1.4924766+11.997571i
#> 23 1.5567004 12.581179 0.44 0.44 1.5567004+12.581179i
#> 24 1.5416669 13.177599 0.46 0.46 1.5416669+13.177599i
#> 25 1.5467639 13.719665 0.48 0.48 1.5467639+13.719665i
#> 26 1.5652715 14.181416 0.50 0.50 1.5652715+14.181416i
#> 27 1.5775083 14.766692 0.52 0.52 1.5775083+14.766692i
#> 28 1.5978045 15.306546 0.54 0.54 1.5978045+15.306546i
#> 29 1.6594418 15.853982 0.56 0.56 1.6594418+15.853982i
#> displacement Trajectory Simulation TrajSim
#> 1 0.000000000+0.0000000i Traj_1 Sim_2 TrajSim_1_2
#> 2 0.027968947+0.5684340i Traj_1 Sim_2 TrajSim_1_2
#> 3 0.031343498+0.5477057i Traj_1 Sim_2 TrajSim_1_2
#> 4 0.064183298+0.4899703i Traj_1 Sim_2 TrajSim_1_2
#> 5 0.082883907+0.5202311i Traj_1 Sim_2 TrajSim_1_2
#> 6 0.025523481+0.5494350i Traj_1 Sim_2 TrajSim_1_2
#> 7 0.058364394+0.6440285i Traj_1 Sim_2 TrajSim_1_2
#> 8 0.023918761+0.5461160i Traj_1 Sim_2 TrajSim_1_2
#> 9 -0.047021979+0.5112088i Traj_1 Sim_2 TrajSim_1_2
#> 10 0.041559778+0.5517729i Traj_1 Sim_2 TrajSim_1_2
#> 11 0.027476096+0.5385288i Traj_1 Sim_2 TrajSim_1_2
#> 12 0.027003701+0.5244901i Traj_1 Sim_2 TrajSim_1_2
#> 13 0.024795330+0.4227235i Traj_1 Sim_2 TrajSim_1_2
#> 14 0.070722957+0.5313885i Traj_1 Sim_2 TrajSim_1_2
#> 15 0.049428906+0.5575814i Traj_1 Sim_2 TrajSim_1_2
#> 16 0.048046356+0.5525771i Traj_1 Sim_2 TrajSim_1_2
#> 17 0.044658482+0.4155105i Traj_1 Sim_2 TrajSim_1_2
#> 18 0.025133099+0.5646602i Traj_1 Sim_2 TrajSim_1_2
#> 19 0.008380457+0.4342959i Traj_1 Sim_2 TrajSim_1_2
#> 20 0.049430468+0.5213057i Traj_1 Sim_2 TrajSim_1_2
#> 21 0.081930589+0.5262034i Traj_1 Sim_2 TrajSim_1_2
#> 22 0.030746036+0.5334041i Traj_1 Sim_2 TrajSim_1_2
#> 23 0.064223828+0.5836074i Traj_1 Sim_2 TrajSim_1_2
#> 24 -0.015033486+0.5964205i Traj_1 Sim_2 TrajSim_1_2
#> 25 0.005096951+0.5420662i Traj_1 Sim_2 TrajSim_1_2
#> 26 0.018507618+0.4617505i Traj_1 Sim_2 TrajSim_1_2
#> 27 0.012236850+0.5852761i Traj_1 Sim_2 TrajSim_1_2
#> 28 0.020296186+0.5398536i Traj_1 Sim_2 TrajSim_1_2
#> 29 0.061637305+0.5474363i Traj_1 Sim_2 TrajSim_1_2
#>
#> [[2]][[2]]
#> x y time displacementTime polar
#> 1 0.3360000 1.560000 0.00 0.00 0.3360000+ 1.560000i
#> 2 0.4798278 2.045927 0.02 0.02 0.4798278+ 2.045927i
#> 3 0.7129478 2.586961 0.04 0.04 0.7129478+ 2.586961i
#> 4 0.9475653 3.110812 0.06 0.06 0.9475653+ 3.110812i
#> 5 1.1896266 3.838410 0.08 0.08 1.1896266+ 3.838410i
#> 6 1.3280812 4.545687 0.10 0.10 1.3280812+ 4.545687i
#> 7 1.4195400 5.049539 0.12 0.12 1.4195400+ 5.049539i
#> 8 1.5801719 5.712272 0.14 0.14 1.5801719+ 5.712272i
#> 9 1.6923081 6.435722 0.16 0.16 1.6923081+ 6.435722i
#> 10 1.8043516 7.019887 0.18 0.18 1.8043516+ 7.019887i
#> 11 1.9508828 7.624103 0.20 0.20 1.9508828+ 7.624103i
#> 12 2.0992015 8.180855 0.22 0.22 2.0992015+ 8.180855i
#> 13 2.3076034 8.757106 0.24 0.24 2.3076034+ 8.757106i
#> 14 2.6580686 9.254722 0.26 0.26 2.6580686+ 9.254722i
#> 15 3.0198705 9.654467 0.28 0.28 3.0198705+ 9.654467i
#> 16 3.3581502 10.091786 0.30 0.30 3.3581502+10.091786i
#> 17 3.7788790 10.429995 0.32 0.32 3.7788790+10.429995i
#> 18 4.3651365 11.048093 0.34 0.34 4.3651365+11.048093i
#> 19 4.6919034 11.534254 0.36 0.36 4.6919034+11.534254i
#> 20 5.1051692 12.024164 0.38 0.38 5.1051692+12.024164i
#> 21 5.5125379 12.556039 0.40 0.40 5.5125379+12.556039i
#> 22 5.8895121 12.847576 0.42 0.42 5.8895121+12.847576i
#> 23 6.3993517 13.351652 0.44 0.44 6.3993517+13.351652i
#> 24 6.8658869 13.624196 0.46 0.46 6.8658869+13.624196i
#> displacement Trajectory Simulation TrajSim
#> 1 0.00000000+0.0000000i Traj_2 Sim_2 TrajSim_2_2
#> 2 0.14382784+0.4859272i Traj_2 Sim_2 TrajSim_2_2
#> 3 0.23312000+0.5410333i Traj_2 Sim_2 TrajSim_2_2
#> 4 0.23461744+0.5238511i Traj_2 Sim_2 TrajSim_2_2
#> 5 0.24206135+0.7275987i Traj_2 Sim_2 TrajSim_2_2
#> 6 0.13845458+0.7072770i Traj_2 Sim_2 TrajSim_2_2
#> 7 0.09145875+0.5038518i Traj_2 Sim_2 TrajSim_2_2
#> 8 0.16063197+0.6627325i Traj_2 Sim_2 TrajSim_2_2
#> 9 0.11213620+0.7234506i Traj_2 Sim_2 TrajSim_2_2
#> 10 0.11204347+0.5841646i Traj_2 Sim_2 TrajSim_2_2
#> 11 0.14653121+0.6042161i Traj_2 Sim_2 TrajSim_2_2
#> 12 0.14831872+0.5567525i Traj_2 Sim_2 TrajSim_2_2
#> 13 0.20840188+0.5762508i Traj_2 Sim_2 TrajSim_2_2
#> 14 0.35046521+0.4976161i Traj_2 Sim_2 TrajSim_2_2
#> 15 0.36180188+0.3997445i Traj_2 Sim_2 TrajSim_2_2
#> 16 0.33827972+0.4373188i Traj_2 Sim_2 TrajSim_2_2
#> 17 0.42072879+0.3382090i Traj_2 Sim_2 TrajSim_2_2
#> 18 0.58625746+0.6180988i Traj_2 Sim_2 TrajSim_2_2
#> 19 0.32676691+0.4861607i Traj_2 Sim_2 TrajSim_2_2
#> 20 0.41326580+0.4899103i Traj_2 Sim_2 TrajSim_2_2
#> 21 0.40736872+0.5318749i Traj_2 Sim_2 TrajSim_2_2
#> 22 0.37697416+0.2915364i Traj_2 Sim_2 TrajSim_2_2
#> 23 0.50983960+0.5040764i Traj_2 Sim_2 TrajSim_2_2
#> 24 0.46653526+0.2725438i Traj_2 Sim_2 TrajSim_2_2
#>
#>
#> [[3]]
#> [[3]][[1]]
#> x y time displacementTime polar
#> 1 0.6960000 0.946000 0.00 0.00 0.6960000+ 0.946000i
#> 2 0.7389433 1.538490 0.02 0.02 0.7389433+ 1.538490i
#> 3 0.7418765 2.038310 0.04 0.04 0.7418765+ 2.038310i
#> 4 0.7437936 2.499058 0.06 0.06 0.7437936+ 2.499058i
#> 5 0.7265755 3.101059 0.08 0.08 0.7265755+ 3.101059i
#> 6 0.7555810 3.613879 0.10 0.10 0.7555810+ 3.613879i
#> 7 0.7583935 4.187719 0.12 0.12 0.7583935+ 4.187719i
#> 8 0.7746257 4.715108 0.14 0.14 0.7746257+ 4.715108i
#> 9 0.7461395 5.245663 0.16 0.16 0.7461395+ 5.245663i
#> 10 0.7400678 5.830331 0.18 0.18 0.7400678+ 5.830331i
#> 11 0.7865814 6.377158 0.20 0.20 0.7865814+ 6.377158i
#> 12 0.8031166 6.840333 0.22 0.22 0.8031166+ 6.840333i
#> 13 0.8384829 7.333355 0.24 0.24 0.8384829+ 7.333355i
#> 14 0.8228265 7.853162 0.26 0.26 0.8228265+ 7.853162i
#> 15 0.8121158 8.413419 0.28 0.28 0.8121158+ 8.413419i
#> 16 0.8450621 8.982518 0.30 0.30 0.8450621+ 8.982518i
#> 17 0.9045730 9.514708 0.32 0.32 0.9045730+ 9.514708i
#> 18 1.0126291 10.046031 0.34 0.34 1.0126291+10.046031i
#> 19 1.0869644 10.576176 0.36 0.36 1.0869644+10.576176i
#> 20 1.1703064 11.130007 0.38 0.38 1.1703064+11.130007i
#> 21 1.2903237 11.631798 0.40 0.40 1.2903237+11.631798i
#> 22 1.3553164 12.151155 0.42 0.42 1.3553164+12.151155i
#> 23 1.4631239 12.661938 0.44 0.44 1.4631239+12.661938i
#> 24 1.4959450 13.221931 0.46 0.46 1.4959450+13.221931i
#> 25 1.5152645 13.692171 0.48 0.48 1.5152645+13.692171i
#> 26 1.4939291 14.312773 0.50 0.50 1.4939291+14.312773i
#> 27 1.5090822 14.869581 0.52 0.52 1.5090822+14.869581i
#> 28 1.4362177 15.429781 0.54 0.54 1.4362177+15.429781i
#> 29 1.3731054 15.967656 0.56 0.56 1.3731054+15.967656i
#> displacement Trajectory Simulation TrajSim
#> 1 0.000000000+0.0000000i Traj_1 Sim_3 TrajSim_1_3
#> 2 0.042943274+0.5924897i Traj_1 Sim_3 TrajSim_1_3
#> 3 0.002933195+0.4998200i Traj_1 Sim_3 TrajSim_1_3
#> 4 0.001917096+0.4607488i Traj_1 Sim_3 TrajSim_1_3
#> 5 -0.017218095+0.6020010i Traj_1 Sim_3 TrajSim_1_3
#> 6 0.029005554+0.5128192i Traj_1 Sim_3 TrajSim_1_3
#> 7 0.002812458+0.5738405i Traj_1 Sim_3 TrajSim_1_3
#> 8 0.016232213+0.5273893i Traj_1 Sim_3 TrajSim_1_3
#> 9 -0.028486191+0.5305546i Traj_1 Sim_3 TrajSim_1_3
#> 10 -0.006071728+0.5846684i Traj_1 Sim_3 TrajSim_1_3
#> 11 0.046513659+0.5468265i Traj_1 Sim_3 TrajSim_1_3
#> 12 0.016535129+0.4631752i Traj_1 Sim_3 TrajSim_1_3
#> 13 0.035366311+0.4930221i Traj_1 Sim_3 TrajSim_1_3
#> 14 -0.015656410+0.5198069i Traj_1 Sim_3 TrajSim_1_3
#> 15 -0.010710646+0.5602565i Traj_1 Sim_3 TrajSim_1_3
#> 16 0.032946319+0.5690990i Traj_1 Sim_3 TrajSim_1_3
#> 17 0.059510843+0.5321909i Traj_1 Sim_3 TrajSim_1_3
#> 18 0.108056155+0.5313223i Traj_1 Sim_3 TrajSim_1_3
#> 19 0.074335275+0.5301456i Traj_1 Sim_3 TrajSim_1_3
#> 20 0.083341939+0.5538309i Traj_1 Sim_3 TrajSim_1_3
#> 21 0.120017363+0.5017913i Traj_1 Sim_3 TrajSim_1_3
#> 22 0.064992663+0.5193567i Traj_1 Sim_3 TrajSim_1_3
#> 23 0.107807555+0.5107826i Traj_1 Sim_3 TrajSim_1_3
#> 24 0.032821072+0.5599934i Traj_1 Sim_3 TrajSim_1_3
#> 25 0.019319528+0.4702397i Traj_1 Sim_3 TrajSim_1_3
#> 26 -0.021335479+0.6206019i Traj_1 Sim_3 TrajSim_1_3
#> 27 0.015153120+0.5568087i Traj_1 Sim_3 TrajSim_1_3
#> 28 -0.072864448+0.5601992i Traj_1 Sim_3 TrajSim_1_3
#> 29 -0.063112299+0.5378754i Traj_1 Sim_3 TrajSim_1_3
#>
#> [[3]][[2]]
#> x y time displacementTime polar
#> 1 0.33600000 1.560000 0.00 0.00 0.33600000+ 1.560000i
#> 2 0.26029470 2.103472 0.02 0.02 0.26029470+ 2.103472i
#> 3 0.09717041 2.682028 0.04 0.04 0.09717041+ 2.682028i
#> 4 -0.05430437 3.286854 0.06 0.06 -0.05430437+ 3.286854i
#> 5 -0.14180685 3.916178 0.08 0.08 -0.14180685+ 3.916178i
#> 6 -0.24806141 4.475867 0.10 0.10 -0.24806141+ 4.475867i
#> 7 -0.28403966 5.089668 0.12 0.12 -0.28403966+ 5.089668i
#> 8 -0.40994362 5.831597 0.14 0.14 -0.40994362+ 5.831597i
#> 9 -0.42875111 6.279125 0.16 0.16 -0.42875111+ 6.279125i
#> 10 -0.35459757 6.989695 0.18 0.18 -0.35459757+ 6.989695i
#> 11 -0.23237453 7.632396 0.20 0.20 -0.23237453+ 7.632396i
#> 12 -0.14353782 8.281654 0.22 0.22 -0.14353782+ 8.281654i
#> 13 0.02869929 8.936307 0.24 0.24 0.02869929+ 8.936307i
#> 14 0.16994215 9.535104 0.26 0.26 0.16994215+ 9.535104i
#> 15 0.24877057 10.187274 0.28 0.28 0.24877057+10.187274i
#> 16 0.28024311 10.899759 0.30 0.30 0.28024311+10.899759i
#> 17 0.26893089 11.613702 0.32 0.32 0.26893089+11.613702i
#> 18 0.17820001 12.328359 0.34 0.34 0.17820001+12.328359i
#> 19 0.02350242 13.002349 0.36 0.36 0.02350242+13.002349i
#> 20 -0.14283224 13.525720 0.38 0.38 -0.14283224+13.525720i
#> 21 -0.38604613 14.030901 0.40 0.40 -0.38604613+14.030901i
#> 22 -0.54740432 14.552060 0.42 0.42 -0.54740432+14.552060i
#> 23 -0.73828215 15.294892 0.44 0.44 -0.73828215+15.294892i
#> 24 -0.91460158 16.013439 0.46 0.46 -0.91460158+16.013439i
#> displacement Trajectory Simulation TrajSim
#> 1 0.00000000+0.0000000i Traj_2 Sim_3 TrajSim_2_3
#> 2 -0.07570530+0.5434720i Traj_2 Sim_3 TrajSim_2_3
#> 3 -0.16312429+0.5785563i Traj_2 Sim_3 TrajSim_2_3
#> 4 -0.15147478+0.6048256i Traj_2 Sim_3 TrajSim_2_3
#> 5 -0.08750248+0.6293240i Traj_2 Sim_3 TrajSim_2_3
#> 6 -0.10625456+0.5596889i Traj_2 Sim_3 TrajSim_2_3
#> 7 -0.03597826+0.6138017i Traj_2 Sim_3 TrajSim_2_3
#> 8 -0.12590396+0.7419285i Traj_2 Sim_3 TrajSim_2_3
#> 9 -0.01880749+0.4475280i Traj_2 Sim_3 TrajSim_2_3
#> 10 0.07415354+0.7105697i Traj_2 Sim_3 TrajSim_2_3
#> 11 0.12222303+0.6427015i Traj_2 Sim_3 TrajSim_2_3
#> 12 0.08883671+0.6492574i Traj_2 Sim_3 TrajSim_2_3
#> 13 0.17223711+0.6546538i Traj_2 Sim_3 TrajSim_2_3
#> 14 0.14124286+0.5987971i Traj_2 Sim_3 TrajSim_2_3
#> 15 0.07882842+0.6521693i Traj_2 Sim_3 TrajSim_2_3
#> 16 0.03147254+0.7124848i Traj_2 Sim_3 TrajSim_2_3
#> 17 -0.01131222+0.7139431i Traj_2 Sim_3 TrajSim_2_3
#> 18 -0.09073089+0.7146570i Traj_2 Sim_3 TrajSim_2_3
#> 19 -0.15469758+0.6739904i Traj_2 Sim_3 TrajSim_2_3
#> 20 -0.16633466+0.5233713i Traj_2 Sim_3 TrajSim_2_3
#> 21 -0.24321389+0.5051810i Traj_2 Sim_3 TrajSim_2_3
#> 22 -0.16135819+0.5211583i Traj_2 Sim_3 TrajSim_2_3
#> 23 -0.19087783+0.7428324i Traj_2 Sim_3 TrajSim_2_3
#> 24 -0.17631944+0.7185465i Traj_2 Sim_3 TrajSim_2_3
#>
#>
#> [[4]]
#> [[4]][[1]]
#> x y time displacementTime polar
#> 1 0.6960000 0.946000 0.00 0.00 0.6960000+ 0.946000i
#> 2 0.6968709 1.517195 0.02 0.02 0.6968709+ 1.517195i
#> 3 0.6279445 2.016373 0.04 0.04 0.6279445+ 2.016373i
#> 4 0.5803911 2.607739 0.06 0.06 0.5803911+ 2.607739i
#> 5 0.5319960 3.151049 0.08 0.08 0.5319960+ 3.151049i
#> 6 0.5224161 3.672039 0.10 0.10 0.5224161+ 3.672039i
#> 7 0.4814294 4.143546 0.12 0.12 0.4814294+ 4.143546i
#> 8 0.4926716 4.653811 0.14 0.14 0.4926716+ 4.653811i
#> 9 0.5267185 5.155130 0.16 0.16 0.5267185+ 5.155130i
#> 10 0.5292116 5.697115 0.18 0.18 0.5292116+ 5.697115i
#> 11 0.4834809 6.294406 0.20 0.20 0.4834809+ 6.294406i
#> 12 0.4579039 6.788959 0.22 0.22 0.4579039+ 6.788959i
#> 13 0.4279417 7.305201 0.24 0.24 0.4279417+ 7.305201i
#> 14 0.4628631 7.822564 0.26 0.26 0.4628631+ 7.822564i
#> 15 0.5266267 8.420821 0.28 0.28 0.5266267+ 8.420821i
#> 16 0.6001109 8.932182 0.30 0.30 0.6001109+ 8.932182i
#> 17 0.5957171 9.433588 0.32 0.32 0.5957171+ 9.433588i
#> 18 0.6075813 9.955984 0.34 0.34 0.6075813+ 9.955984i
#> 19 0.6505353 10.541241 0.36 0.36 0.6505353+10.541241i
#> 20 0.6259161 11.135502 0.38 0.38 0.6259161+11.135502i
#> 21 0.6506040 11.663818 0.40 0.40 0.6506040+11.663818i
#> 22 0.6808540 12.144403 0.42 0.42 0.6808540+12.144403i
#> 23 0.6671461 12.604062 0.44 0.44 0.6671461+12.604062i
#> 24 0.6837512 13.142536 0.46 0.46 0.6837512+13.142536i
#> 25 0.6628320 13.702095 0.48 0.48 0.6628320+13.702095i
#> 26 0.6662988 14.251632 0.50 0.50 0.6662988+14.251632i
#> 27 0.7147287 14.784549 0.52 0.52 0.7147287+14.784549i
#> 28 0.7343856 15.253413 0.54 0.54 0.7343856+15.253413i
#> 29 0.7929100 15.781797 0.56 0.56 0.7929100+15.781797i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000000+0.0000000i Traj_1 Sim_4 TrajSim_1_4
#> 2 0.0008708749+0.5711946i Traj_1 Sim_4 TrajSim_1_4
#> 3 -0.0689263655+0.4991784i Traj_1 Sim_4 TrajSim_1_4
#> 4 -0.0475533985+0.5913665i Traj_1 Sim_4 TrajSim_1_4
#> 5 -0.0483950705+0.5433093i Traj_1 Sim_4 TrajSim_1_4
#> 6 -0.0095799217+0.5209907i Traj_1 Sim_4 TrajSim_1_4
#> 7 -0.0409867436+0.4715062i Traj_1 Sim_4 TrajSim_1_4
#> 8 0.0112422468+0.5102650i Traj_1 Sim_4 TrajSim_1_4
#> 9 0.0340468693+0.5013194i Traj_1 Sim_4 TrajSim_1_4
#> 10 0.0024930771+0.5419851i Traj_1 Sim_4 TrajSim_1_4
#> 11 -0.0457307127+0.5972913i Traj_1 Sim_4 TrajSim_1_4
#> 12 -0.0255769356+0.4945521i Traj_1 Sim_4 TrajSim_1_4
#> 13 -0.0299622167+0.5162426i Traj_1 Sim_4 TrajSim_1_4
#> 14 0.0349214098+0.5173625i Traj_1 Sim_4 TrajSim_1_4
#> 15 0.0637635783+0.5982576i Traj_1 Sim_4 TrajSim_1_4
#> 16 0.0734841633+0.5113607i Traj_1 Sim_4 TrajSim_1_4
#> 17 -0.0043937941+0.5014065i Traj_1 Sim_4 TrajSim_1_4
#> 18 0.0118642729+0.5223957i Traj_1 Sim_4 TrajSim_1_4
#> 19 0.0429539624+0.5852573i Traj_1 Sim_4 TrajSim_1_4
#> 20 -0.0246191851+0.5942610i Traj_1 Sim_4 TrajSim_1_4
#> 21 0.0246879067+0.5283158i Traj_1 Sim_4 TrajSim_1_4
#> 22 0.0302499767+0.4805847i Traj_1 Sim_4 TrajSim_1_4
#> 23 -0.0137079021+0.4596595i Traj_1 Sim_4 TrajSim_1_4
#> 24 0.0166050622+0.5384740i Traj_1 Sim_4 TrajSim_1_4
#> 25 -0.0209191651+0.5595589i Traj_1 Sim_4 TrajSim_1_4
#> 26 0.0034667832+0.5495367i Traj_1 Sim_4 TrajSim_1_4
#> 27 0.0484299688+0.5329166i Traj_1 Sim_4 TrajSim_1_4
#> 28 0.0196568394+0.4688644i Traj_1 Sim_4 TrajSim_1_4
#> 29 0.0585244022+0.5283841i Traj_1 Sim_4 TrajSim_1_4
#>
#> [[4]][[2]]
#> x y time displacementTime polar
#> 1 0.3360000 1.560000 0.00 0.00 0.3360000+ 1.560000i
#> 2 0.4870226 2.077005 0.02 0.02 0.4870226+ 2.077005i
#> 3 0.7631969 2.731979 0.04 0.04 0.7631969+ 2.731979i
#> 4 1.1045809 3.214528 0.06 0.06 1.1045809+ 3.214528i
#> 5 1.4016623 3.589900 0.08 0.08 1.4016623+ 3.589900i
#> 6 1.6507562 4.107133 0.10 0.10 1.6507562+ 4.107133i
#> 7 1.9793976 4.536114 0.12 0.12 1.9793976+ 4.536114i
#> 8 2.3824778 4.980269 0.14 0.14 2.3824778+ 4.980269i
#> 9 2.7341933 5.312535 0.16 0.16 2.7341933+ 5.312535i
#> 10 3.1151562 5.841121 0.18 0.18 3.1151562+ 5.841121i
#> 11 3.4345879 6.517675 0.20 0.20 3.4345879+ 6.517675i
#> 12 3.7091482 7.116195 0.22 0.22 3.7091482+ 7.116195i
#> 13 3.9654127 7.747333 0.24 0.24 3.9654127+ 7.747333i
#> 14 4.0888288 8.434998 0.26 0.26 4.0888288+ 8.434998i
#> 15 4.1712164 9.051800 0.28 0.28 4.1712164+ 9.051800i
#> 16 4.1922717 9.757923 0.30 0.30 4.1922717+ 9.757923i
#> 17 4.3139250 10.306731 0.32 0.32 4.3139250+10.306731i
#> 18 4.4227932 10.978672 0.34 0.34 4.4227932+10.978672i
#> 19 4.4270939 11.579956 0.36 0.36 4.4270939+11.579956i
#> 20 4.5033260 12.197951 0.38 0.38 4.5033260+12.197951i
#> 21 4.4490793 12.857164 0.40 0.40 4.4490793+12.857164i
#> 22 4.3769387 13.421788 0.42 0.42 4.3769387+13.421788i
#> 23 4.3292488 14.027644 0.44 0.44 4.3292488+14.027644i
#> 24 4.2106753 14.630669 0.46 0.46 4.2106753+14.630669i
#> displacement Trajectory Simulation TrajSim
#> 1 0.000000000+0.0000000i Traj_2 Sim_4 TrajSim_2_4
#> 2 0.151022649+0.5170053i Traj_2 Sim_4 TrajSim_2_4
#> 3 0.276174215+0.6549738i Traj_2 Sim_4 TrajSim_2_4
#> 4 0.341384081+0.4825492i Traj_2 Sim_4 TrajSim_2_4
#> 5 0.297081346+0.3753720i Traj_2 Sim_4 TrajSim_2_4
#> 6 0.249093920+0.5172326i Traj_2 Sim_4 TrajSim_2_4
#> 7 0.328641427+0.4289810i Traj_2 Sim_4 TrajSim_2_4
#> 8 0.403080117+0.4441549i Traj_2 Sim_4 TrajSim_2_4
#> 9 0.351715523+0.3322663i Traj_2 Sim_4 TrajSim_2_4
#> 10 0.380962890+0.5285863i Traj_2 Sim_4 TrajSim_2_4
#> 11 0.319431694+0.6765538i Traj_2 Sim_4 TrajSim_2_4
#> 12 0.274560351+0.5985197i Traj_2 Sim_4 TrajSim_2_4
#> 13 0.256264508+0.6311382i Traj_2 Sim_4 TrajSim_2_4
#> 14 0.123416121+0.6876650i Traj_2 Sim_4 TrajSim_2_4
#> 15 0.082387572+0.6168020i Traj_2 Sim_4 TrajSim_2_4
#> 16 0.021055252+0.7061225i Traj_2 Sim_4 TrajSim_2_4
#> 17 0.121653341+0.5488085i Traj_2 Sim_4 TrajSim_2_4
#> 18 0.108868228+0.6719406i Traj_2 Sim_4 TrajSim_2_4
#> 19 0.004300654+0.6012845i Traj_2 Sim_4 TrajSim_2_4
#> 20 0.076232082+0.6179947i Traj_2 Sim_4 TrajSim_2_4
#> 21 -0.054246633+0.6592131i Traj_2 Sim_4 TrajSim_2_4
#> 22 -0.072140600+0.5646242i Traj_2 Sim_4 TrajSim_2_4
#> 23 -0.047689903+0.6058561i Traj_2 Sim_4 TrajSim_2_4
#> 24 -0.118573487+0.6030246i Traj_2 Sim_4 TrajSim_2_4
#>
#>
#> [[5]]
#> [[5]][[1]]
#> x y time displacementTime polar
#> 1 0.69600000 0.946000 0.00 0.00 0.69600000+ 0.946000i
#> 2 0.73743342 1.405394 0.02 0.02 0.73743342+ 1.405394i
#> 3 0.74337116 1.977781 0.04 0.04 0.74337116+ 1.977781i
#> 4 0.77432062 2.420490 0.06 0.06 0.77432062+ 2.420490i
#> 5 0.77809104 2.889732 0.08 0.08 0.77809104+ 2.889732i
#> 6 0.72875077 3.367813 0.10 0.10 0.72875077+ 3.367813i
#> 7 0.66960504 3.862699 0.12 0.12 0.66960504+ 3.862699i
#> 8 0.67322327 4.565207 0.14 0.14 0.67322327+ 4.565207i
#> 9 0.68462544 5.166350 0.16 0.16 0.68462544+ 5.166350i
#> 10 0.69049448 5.734952 0.18 0.18 0.69049448+ 5.734952i
#> 11 0.66411357 6.274849 0.20 0.20 0.66411357+ 6.274849i
#> 12 0.62868359 6.880611 0.22 0.22 0.62868359+ 6.880611i
#> 13 0.57542658 7.357341 0.24 0.24 0.57542658+ 7.357341i
#> 14 0.48853002 7.959711 0.26 0.26 0.48853002+ 7.959711i
#> 15 0.43686205 8.379161 0.28 0.28 0.43686205+ 8.379161i
#> 16 0.35343168 8.896010 0.30 0.30 0.35343168+ 8.896010i
#> 17 0.28197382 9.418634 0.32 0.32 0.28197382+ 9.418634i
#> 18 0.22763029 9.885400 0.34 0.34 0.22763029+ 9.885400i
#> 19 0.16211661 10.424940 0.36 0.36 0.16211661+10.424940i
#> 20 0.08951733 10.950409 0.38 0.38 0.08951733+10.950409i
#> 21 -0.01848653 11.484603 0.40 0.40 -0.01848653+11.484603i
#> 22 -0.08807650 11.975995 0.42 0.42 -0.08807650+11.975995i
#> 23 -0.14664870 12.469282 0.44 0.44 -0.14664870+12.469282i
#> 24 -0.24156227 13.064004 0.46 0.46 -0.24156227+13.064004i
#> 25 -0.34707462 13.577955 0.48 0.48 -0.34707462+13.577955i
#> 26 -0.43781412 14.048914 0.50 0.50 -0.43781412+14.048914i
#> 27 -0.61819243 14.702123 0.52 0.52 -0.61819243+14.702123i
#> 28 -0.72957953 15.111581 0.54 0.54 -0.72957953+15.111581i
#> 29 -0.94034993 15.699217 0.56 0.56 -0.94034993+15.699217i
#> displacement Trajectory Simulation TrajSim
#> 1 0.000000000+0.0000000i Traj_1 Sim_5 TrajSim_1_5
#> 2 0.041433416+0.4593943i Traj_1 Sim_5 TrajSim_1_5
#> 3 0.005937749+0.5723870i Traj_1 Sim_5 TrajSim_1_5
#> 4 0.030949456+0.4427090i Traj_1 Sim_5 TrajSim_1_5
#> 5 0.003770414+0.4692414i Traj_1 Sim_5 TrajSim_1_5
#> 6 -0.049340263+0.4780808i Traj_1 Sim_5 TrajSim_1_5
#> 7 -0.059145734+0.4948870i Traj_1 Sim_5 TrajSim_1_5
#> 8 0.003618235+0.7025074i Traj_1 Sim_5 TrajSim_1_5
#> 9 0.011402172+0.6011427i Traj_1 Sim_5 TrajSim_1_5
#> 10 0.005869032+0.5686024i Traj_1 Sim_5 TrajSim_1_5
#> 11 -0.026380910+0.5398973i Traj_1 Sim_5 TrajSim_1_5
#> 12 -0.035429974+0.6057616i Traj_1 Sim_5 TrajSim_1_5
#> 13 -0.053257008+0.4767302i Traj_1 Sim_5 TrajSim_1_5
#> 14 -0.086896567+0.6023693i Traj_1 Sim_5 TrajSim_1_5
#> 15 -0.051667971+0.4194509i Traj_1 Sim_5 TrajSim_1_5
#> 16 -0.083430365+0.5168486i Traj_1 Sim_5 TrajSim_1_5
#> 17 -0.071457864+0.5226243i Traj_1 Sim_5 TrajSim_1_5
#> 18 -0.054343530+0.4667653i Traj_1 Sim_5 TrajSim_1_5
#> 19 -0.065513675+0.5395402i Traj_1 Sim_5 TrajSim_1_5
#> 20 -0.072599280+0.5254687i Traj_1 Sim_5 TrajSim_1_5
#> 21 -0.108003865+0.5341942i Traj_1 Sim_5 TrajSim_1_5
#> 22 -0.069589962+0.4913923i Traj_1 Sim_5 TrajSim_1_5
#> 23 -0.058572206+0.4932873i Traj_1 Sim_5 TrajSim_1_5
#> 24 -0.094913570+0.5947214i Traj_1 Sim_5 TrajSim_1_5
#> 25 -0.105512354+0.5139512i Traj_1 Sim_5 TrajSim_1_5
#> 26 -0.090739497+0.4709592i Traj_1 Sim_5 TrajSim_1_5
#> 27 -0.180378310+0.6532085i Traj_1 Sim_5 TrajSim_1_5
#> 28 -0.111387102+0.4094582i Traj_1 Sim_5 TrajSim_1_5
#> 29 -0.210770396+0.5876363i Traj_1 Sim_5 TrajSim_1_5
#>
#> [[5]][[2]]
#> x y time displacementTime polar
#> 1 0.3360000 1.560000 0.00 0.00 0.3360000+ 1.560000i
#> 2 0.5314512 2.196778 0.02 0.02 0.5314512+ 2.196778i
#> 3 0.8473264 2.769259 0.04 0.04 0.8473264+ 2.769259i
#> 4 1.1626713 3.286546 0.06 0.06 1.1626713+ 3.286546i
#> 5 1.4389417 3.798284 0.08 0.08 1.4389417+ 3.798284i
#> 6 1.6238892 4.309926 0.10 0.10 1.6238892+ 4.309926i
#> 7 1.7870967 4.798690 0.12 0.12 1.7870967+ 4.798690i
#> 8 1.9742929 5.354762 0.14 0.14 1.9742929+ 5.354762i
#> 9 2.1681724 5.945715 0.16 0.16 2.1681724+ 5.945715i
#> 10 2.3576160 6.596670 0.18 0.18 2.3576160+ 6.596670i
#> 11 2.4277517 7.282783 0.20 0.20 2.4277517+ 7.282783i
#> 12 2.4186463 7.938605 0.22 0.22 2.4186463+ 7.938605i
#> 13 2.4343472 8.687339 0.24 0.24 2.4343472+ 8.687339i
#> 14 2.3410029 9.441496 0.26 0.26 2.3410029+ 9.441496i
#> 15 2.2398308 10.106612 0.28 0.28 2.2398308+10.106612i
#> 16 2.0249372 10.769590 0.30 0.30 2.0249372+10.769590i
#> 17 1.9575258 11.406937 0.32 0.32 1.9575258+11.406937i
#> 18 1.8529934 12.090561 0.34 0.34 1.8529934+12.090561i
#> 19 1.8091371 12.634850 0.36 0.36 1.8091371+12.634850i
#> 20 1.8373749 13.106663 0.38 0.38 1.8373749+13.106663i
#> 21 1.8656629 13.738455 0.40 0.40 1.8656629+13.738455i
#> 22 1.9050465 14.407686 0.42 0.42 1.9050465+14.407686i
#> 23 1.9367074 15.071140 0.44 0.44 1.9367074+15.071140i
#> 24 2.1073010 15.732577 0.46 0.46 2.1073010+15.732577i
#> displacement Trajectory Simulation TrajSim
#> 1 0.000000000+0.0000000i Traj_2 Sim_5 TrajSim_2_5
#> 2 0.195451247+0.6367781i Traj_2 Sim_5 TrajSim_2_5
#> 3 0.315875198+0.5724807i Traj_2 Sim_5 TrajSim_2_5
#> 4 0.315344840+0.5172870i Traj_2 Sim_5 TrajSim_2_5
#> 5 0.276270383+0.5117383i Traj_2 Sim_5 TrajSim_2_5
#> 6 0.184947525+0.5116415i Traj_2 Sim_5 TrajSim_2_5
#> 7 0.163207479+0.4887644i Traj_2 Sim_5 TrajSim_2_5
#> 8 0.187196211+0.5560721i Traj_2 Sim_5 TrajSim_2_5
#> 9 0.193879472+0.5909528i Traj_2 Sim_5 TrajSim_2_5
#> 10 0.189443688+0.6509552i Traj_2 Sim_5 TrajSim_2_5
#> 11 0.070135629+0.6861130i Traj_2 Sim_5 TrajSim_2_5
#> 12 -0.009105397+0.6558214i Traj_2 Sim_5 TrajSim_2_5
#> 13 0.015700905+0.7487347i Traj_2 Sim_5 TrajSim_2_5
#> 14 -0.093344287+0.7541569i Traj_2 Sim_5 TrajSim_2_5
#> 15 -0.101172096+0.6651155i Traj_2 Sim_5 TrajSim_2_5
#> 16 -0.214893603+0.6629781i Traj_2 Sim_5 TrajSim_2_5
#> 17 -0.067411397+0.6373471i Traj_2 Sim_5 TrajSim_2_5
#> 18 -0.104532381+0.6836239i Traj_2 Sim_5 TrajSim_2_5
#> 19 -0.043856350+0.5442897i Traj_2 Sim_5 TrajSim_2_5
#> 20 0.028237876+0.4718127i Traj_2 Sim_5 TrajSim_2_5
#> 21 0.028287911+0.6317919i Traj_2 Sim_5 TrajSim_2_5
#> 22 0.039383611+0.6692309i Traj_2 Sim_5 TrajSim_2_5
#> 23 0.031660983+0.6634545i Traj_2 Sim_5 TrajSim_2_5
#> 24 0.170593534+0.6614364i Traj_2 Sim_5 TrajSim_2_5
#>
#>
#> [[6]]
#> [[6]][[1]]
#> x y time displacementTime polar
#> 1 0.6960000 0.946000 0.00 0.00 0.6960000+ 0.946000i
#> 2 0.6783104 1.541369 0.02 0.02 0.6783104+ 1.541369i
#> 3 0.6634019 2.057164 0.04 0.04 0.6634019+ 2.057164i
#> 4 0.6978697 2.630188 0.06 0.06 0.6978697+ 2.630188i
#> 5 0.7540260 3.194751 0.08 0.08 0.7540260+ 3.194751i
#> 6 0.8604221 3.712630 0.10 0.10 0.8604221+ 3.712630i
#> 7 0.9348046 4.169155 0.12 0.12 0.9348046+ 4.169155i
#> 8 0.9870172 4.597726 0.14 0.14 0.9870172+ 4.597726i
#> 9 1.0483942 5.145833 0.16 0.16 1.0483942+ 5.145833i
#> 10 1.1834474 5.713513 0.18 0.18 1.1834474+ 5.713513i
#> 11 1.2911690 6.185826 0.20 0.20 1.2911690+ 6.185826i
#> 12 1.4204920 6.647713 0.22 0.22 1.4204920+ 6.647713i
#> 13 1.5510058 7.199406 0.24 0.24 1.5510058+ 7.199406i
#> 14 1.6937957 7.773197 0.26 0.26 1.6937957+ 7.773197i
#> 15 1.7424385 8.280992 0.28 0.28 1.7424385+ 8.280992i
#> 16 1.7696307 8.810046 0.30 0.30 1.7696307+ 8.810046i
#> 17 1.8061303 9.291518 0.32 0.32 1.8061303+ 9.291518i
#> 18 1.8303791 9.826950 0.34 0.34 1.8303791+ 9.826950i
#> 19 1.8759900 10.400619 0.36 0.36 1.8759900+10.400619i
#> 20 1.9203637 10.915020 0.38 0.38 1.9203637+10.915020i
#> 21 1.9864939 11.371582 0.40 0.40 1.9864939+11.371582i
#> 22 2.0821710 11.965361 0.42 0.42 2.0821710+11.965361i
#> 23 2.1579234 12.451196 0.44 0.44 2.1579234+12.451196i
#> 24 2.2341661 12.957236 0.46 0.46 2.2341661+12.957236i
#> 25 2.2757677 13.502949 0.48 0.48 2.2757677+13.502949i
#> 26 2.3370667 14.015140 0.50 0.50 2.3370667+14.015140i
#> 27 2.4313258 14.518404 0.52 0.52 2.4313258+14.518404i
#> 28 2.4951485 14.997885 0.54 0.54 2.4951485+14.997885i
#> 29 2.5865019 15.473539 0.56 0.56 2.5865019+15.473539i
#> displacement Trajectory Simulation TrajSim
#> 1 0.00000000+0.0000000i Traj_1 Sim_6 TrajSim_1_6
#> 2 -0.01768956+0.5953692i Traj_1 Sim_6 TrajSim_1_6
#> 3 -0.01490851+0.5157944i Traj_1 Sim_6 TrajSim_1_6
#> 4 0.03446772+0.5730249i Traj_1 Sim_6 TrajSim_1_6
#> 5 0.05615638+0.5645621i Traj_1 Sim_6 TrajSim_1_6
#> 6 0.10639609+0.5178796i Traj_1 Sim_6 TrajSim_1_6
#> 7 0.07438252+0.4565246i Traj_1 Sim_6 TrajSim_1_6
#> 8 0.05221256+0.4285714i Traj_1 Sim_6 TrajSim_1_6
#> 9 0.06137703+0.5481068i Traj_1 Sim_6 TrajSim_1_6
#> 10 0.13505319+0.5676802i Traj_1 Sim_6 TrajSim_1_6
#> 11 0.10772160+0.4723130i Traj_1 Sim_6 TrajSim_1_6
#> 12 0.12932296+0.4618867i Traj_1 Sim_6 TrajSim_1_6
#> 13 0.13051379+0.5516929i Traj_1 Sim_6 TrajSim_1_6
#> 14 0.14278991+0.5737911i Traj_1 Sim_6 TrajSim_1_6
#> 15 0.04864286+0.5077957i Traj_1 Sim_6 TrajSim_1_6
#> 16 0.02719220+0.5290537i Traj_1 Sim_6 TrajSim_1_6
#> 17 0.03649959+0.4814720i Traj_1 Sim_6 TrajSim_1_6
#> 18 0.02424875+0.5354316i Traj_1 Sim_6 TrajSim_1_6
#> 19 0.04561092+0.5736697i Traj_1 Sim_6 TrajSim_1_6
#> 20 0.04437366+0.5144002i Traj_1 Sim_6 TrajSim_1_6
#> 21 0.06613028+0.4565622i Traj_1 Sim_6 TrajSim_1_6
#> 22 0.09567702+0.5937787i Traj_1 Sim_6 TrajSim_1_6
#> 23 0.07575243+0.4858354i Traj_1 Sim_6 TrajSim_1_6
#> 24 0.07624269+0.5060399i Traj_1 Sim_6 TrajSim_1_6
#> 25 0.04160159+0.5457131i Traj_1 Sim_6 TrajSim_1_6
#> 26 0.06129906+0.5121908i Traj_1 Sim_6 TrajSim_1_6
#> 27 0.09425902+0.5032638i Traj_1 Sim_6 TrajSim_1_6
#> 28 0.06382279+0.4794813i Traj_1 Sim_6 TrajSim_1_6
#> 29 0.09135332+0.4756542i Traj_1 Sim_6 TrajSim_1_6
#>
#> [[6]][[2]]
#> x y time displacementTime polar
#> 1 0.33600000 1.560000 0.00 0.00 0.33600000+ 1.560000i
#> 2 0.34466374 2.095035 0.02 0.02 0.34466374+ 2.095035i
#> 3 0.37914651 2.759714 0.04 0.04 0.37914651+ 2.759714i
#> 4 0.31712100 3.304457 0.06 0.06 0.31712100+ 3.304457i
#> 5 0.24338122 3.790072 0.08 0.08 0.24338122+ 3.790072i
#> 6 0.23182741 4.230156 0.10 0.10 0.23182741+ 4.230156i
#> 7 0.22203847 4.761424 0.12 0.12 0.22203847+ 4.761424i
#> 8 0.07887612 5.467559 0.14 0.14 0.07887612+ 5.467559i
#> 9 -0.13342424 5.981037 0.16 0.16 -0.13342424+ 5.981037i
#> 10 -0.40855354 6.490474 0.18 0.18 -0.40855354+ 6.490474i
#> 11 -0.64143288 7.082908 0.20 0.20 -0.64143288+ 7.082908i
#> 12 -0.91813226 7.659880 0.22 0.22 -0.91813226+ 7.659880i
#> 13 -1.08699808 8.187691 0.24 0.24 -1.08699808+ 8.187691i
#> 14 -1.29087154 8.876023 0.26 0.26 -1.29087154+ 8.876023i
#> 15 -1.43842943 9.348323 0.28 0.28 -1.43842943+ 9.348323i
#> 16 -1.61955594 9.990803 0.30 0.30 -1.61955594+ 9.990803i
#> 17 -1.73276116 10.601450 0.32 0.32 -1.73276116+10.601450i
#> 18 -1.90440535 11.295213 0.34 0.34 -1.90440535+11.295213i
#> 19 -1.99168060 11.822179 0.36 0.36 -1.99168060+11.822179i
#> 20 -2.04369892 12.351857 0.38 0.38 -2.04369892+12.351857i
#> 21 -1.93824790 12.878259 0.40 0.40 -1.93824790+12.878259i
#> 22 -1.78471979 13.542991 0.42 0.42 -1.78471979+13.542991i
#> 23 -1.59572449 14.257658 0.44 0.44 -1.59572449+14.257658i
#> 24 -1.54016691 14.916477 0.46 0.46 -1.54016691+14.916477i
#> displacement Trajectory Simulation TrajSim
#> 1 0.000000000+0.0000000i Traj_2 Sim_6 TrajSim_2_6
#> 2 0.008663736+0.5350350i Traj_2 Sim_6 TrajSim_2_6
#> 3 0.034482772+0.6646786i Traj_2 Sim_6 TrajSim_2_6
#> 4 -0.062025508+0.5447430i Traj_2 Sim_6 TrajSim_2_6
#> 5 -0.073739777+0.4856154i Traj_2 Sim_6 TrajSim_2_6
#> 6 -0.011553814+0.4400843i Traj_2 Sim_6 TrajSim_2_6
#> 7 -0.009788938+0.5312675i Traj_2 Sim_6 TrajSim_2_6
#> 8 -0.143162348+0.7061353i Traj_2 Sim_6 TrajSim_2_6
#> 9 -0.212300360+0.5134776i Traj_2 Sim_6 TrajSim_2_6
#> 10 -0.275129299+0.5094378i Traj_2 Sim_6 TrajSim_2_6
#> 11 -0.232879343+0.5924341i Traj_2 Sim_6 TrajSim_2_6
#> 12 -0.276699379+0.5769711i Traj_2 Sim_6 TrajSim_2_6
#> 13 -0.168865820+0.5278113i Traj_2 Sim_6 TrajSim_2_6
#> 14 -0.203873465+0.6883326i Traj_2 Sim_6 TrajSim_2_6
#> 15 -0.147557883+0.4722992i Traj_2 Sim_6 TrajSim_2_6
#> 16 -0.181126512+0.6424800i Traj_2 Sim_6 TrajSim_2_6
#> 17 -0.113205221+0.6106474i Traj_2 Sim_6 TrajSim_2_6
#> 18 -0.171644189+0.6937633i Traj_2 Sim_6 TrajSim_2_6
#> 19 -0.087275255+0.5269658i Traj_2 Sim_6 TrajSim_2_6
#> 20 -0.052018316+0.5296783i Traj_2 Sim_6 TrajSim_2_6
#> 21 0.105451015+0.5264012i Traj_2 Sim_6 TrajSim_2_6
#> 22 0.153528119+0.6647327i Traj_2 Sim_6 TrajSim_2_6
#> 23 0.188995294+0.7146670i Traj_2 Sim_6 TrajSim_2_6
#> 24 0.055557583+0.6588187i Traj_2 Sim_6 TrajSim_2_6
#>
#>
#> [[7]]
#> [[7]][[1]]
#> x y time displacementTime polar
#> 1 0.6960000 0.946000 0.00 0.00 0.6960000+ 0.946000i
#> 2 0.7309547 1.497184 0.02 0.02 0.7309547+ 1.497184i
#> 3 0.8021750 2.045951 0.04 0.04 0.8021750+ 2.045951i
#> 4 0.8397647 2.632072 0.06 0.06 0.8397647+ 2.632072i
#> 5 0.8633038 3.116389 0.08 0.08 0.8633038+ 3.116389i
#> 6 0.9583418 3.707217 0.10 0.10 0.9583418+ 3.707217i
#> 7 1.0184262 4.208360 0.12 0.12 1.0184262+ 4.208360i
#> 8 1.0719173 4.777339 0.14 0.14 1.0719173+ 4.777339i
#> 9 1.1431095 5.267953 0.16 0.16 1.1431095+ 5.267953i
#> 10 1.2309080 5.813583 0.18 0.18 1.2309080+ 5.813583i
#> 11 1.3144867 6.339854 0.20 0.20 1.3144867+ 6.339854i
#> 12 1.3948463 6.875206 0.22 0.22 1.3948463+ 6.875206i
#> 13 1.4503509 7.427798 0.24 0.24 1.4503509+ 7.427798i
#> 14 1.4962631 7.952952 0.26 0.26 1.4962631+ 7.952952i
#> 15 1.5350766 8.423497 0.28 0.28 1.5350766+ 8.423497i
#> 16 1.6025926 8.967829 0.30 0.30 1.6025926+ 8.967829i
#> 17 1.6331356 9.381763 0.32 0.32 1.6331356+ 9.381763i
#> 18 1.6429991 9.967576 0.34 0.34 1.6429991+ 9.967576i
#> 19 1.6049842 10.503049 0.36 0.36 1.6049842+10.503049i
#> 20 1.5764934 11.115981 0.38 0.38 1.5764934+11.115981i
#> 21 1.4959543 11.608423 0.40 0.40 1.4959543+11.608423i
#> 22 1.3883688 12.120034 0.42 0.42 1.3883688+12.120034i
#> 23 1.2007259 12.699988 0.44 0.44 1.2007259+12.699988i
#> 24 1.0115839 13.184870 0.46 0.46 1.0115839+13.184870i
#> 25 0.8424177 13.622273 0.48 0.48 0.8424177+13.622273i
#> 26 0.6966391 14.045105 0.50 0.50 0.6966391+14.045105i
#> 27 0.5166188 14.651059 0.52 0.52 0.5166188+14.651059i
#> 28 0.3690189 15.141382 0.54 0.54 0.3690189+15.141382i
#> 29 0.2379506 15.588814 0.56 0.56 0.2379506+15.588814i
#> displacement Trajectory Simulation TrajSim
#> 1 0.000000000+0.0000000i Traj_1 Sim_7 TrajSim_1_7
#> 2 0.034954748+0.5511841i Traj_1 Sim_7 TrajSim_1_7
#> 3 0.071220278+0.5487666i Traj_1 Sim_7 TrajSim_1_7
#> 4 0.037589718+0.5861213i Traj_1 Sim_7 TrajSim_1_7
#> 5 0.023539076+0.4843168i Traj_1 Sim_7 TrajSim_1_7
#> 6 0.095038011+0.5908284i Traj_1 Sim_7 TrajSim_1_7
#> 7 0.060084324+0.5011428i Traj_1 Sim_7 TrajSim_1_7
#> 8 0.053491162+0.5689790i Traj_1 Sim_7 TrajSim_1_7
#> 9 0.071192149+0.4906135i Traj_1 Sim_7 TrajSim_1_7
#> 10 0.087798497+0.5456304i Traj_1 Sim_7 TrajSim_1_7
#> 11 0.083578704+0.5262707i Traj_1 Sim_7 TrajSim_1_7
#> 12 0.080359652+0.5353522i Traj_1 Sim_7 TrajSim_1_7
#> 13 0.055504552+0.5525917i Traj_1 Sim_7 TrajSim_1_7
#> 14 0.045912268+0.5251539i Traj_1 Sim_7 TrajSim_1_7
#> 15 0.038813475+0.4705456i Traj_1 Sim_7 TrajSim_1_7
#> 16 0.067515994+0.5443316i Traj_1 Sim_7 TrajSim_1_7
#> 17 0.030543019+0.4139343i Traj_1 Sim_7 TrajSim_1_7
#> 18 0.009863508+0.5858133i Traj_1 Sim_7 TrajSim_1_7
#> 19 -0.038014906+0.5354724i Traj_1 Sim_7 TrajSim_1_7
#> 20 -0.028490795+0.6129320i Traj_1 Sim_7 TrajSim_1_7
#> 21 -0.080539132+0.4924424i Traj_1 Sim_7 TrajSim_1_7
#> 22 -0.107585524+0.5116115i Traj_1 Sim_7 TrajSim_1_7
#> 23 -0.187642827+0.5799539i Traj_1 Sim_7 TrajSim_1_7
#> 24 -0.189142047+0.4848817i Traj_1 Sim_7 TrajSim_1_7
#> 25 -0.169166220+0.4374025i Traj_1 Sim_7 TrajSim_1_7
#> 26 -0.145778619+0.4228323i Traj_1 Sim_7 TrajSim_1_7
#> 27 -0.180020218+0.6059537i Traj_1 Sim_7 TrajSim_1_7
#> 28 -0.147599969+0.4903235i Traj_1 Sim_7 TrajSim_1_7
#> 29 -0.131068242+0.4474324i Traj_1 Sim_7 TrajSim_1_7
#>
#> [[7]][[2]]
#> x y time displacementTime polar
#> 1 0.33600000 1.560000 0.00 0.00 0.33600000+ 1.560000i
#> 2 0.47985659 2.321785 0.02 0.02 0.47985659+ 2.321785i
#> 3 0.58466596 2.879145 0.04 0.04 0.58466596+ 2.879145i
#> 4 0.69911359 3.376649 0.06 0.06 0.69911359+ 3.376649i
#> 5 0.79548798 3.990511 0.08 0.08 0.79548798+ 3.990511i
#> 6 0.83352705 4.496456 0.10 0.10 0.83352705+ 4.496456i
#> 7 0.77588536 5.127976 0.12 0.12 0.77588536+ 5.127976i
#> 8 0.80620784 5.718532 0.14 0.14 0.80620784+ 5.718532i
#> 9 0.85926052 6.211061 0.16 0.16 0.85926052+ 6.211061i
#> 10 0.89629414 6.681276 0.18 0.18 0.89629414+ 6.681276i
#> 11 0.85128536 7.355897 0.20 0.20 0.85128536+ 7.355897i
#> 12 0.81017098 7.948934 0.22 0.22 0.81017098+ 7.948934i
#> 13 0.72904102 8.464798 0.24 0.24 0.72904102+ 8.464798i
#> 14 0.72343819 9.068934 0.26 0.26 0.72343819+ 9.068934i
#> 15 0.61142724 9.754527 0.28 0.28 0.61142724+ 9.754527i
#> 16 0.46979623 10.391166 0.30 0.30 0.46979623+10.391166i
#> 17 0.34660327 10.958009 0.32 0.32 0.34660327+10.958009i
#> 18 0.35941146 11.690937 0.34 0.34 0.35941146+11.690937i
#> 19 0.35709127 12.170429 0.36 0.36 0.35709127+12.170429i
#> 20 0.35210971 12.734381 0.38 0.38 0.35210971+12.734381i
#> 21 0.24989069 13.215631 0.40 0.40 0.24989069+13.215631i
#> 22 0.15630887 13.776018 0.42 0.42 0.15630887+13.776018i
#> 23 -0.04776026 14.247336 0.44 0.44 -0.04776026+14.247336i
#> 24 -0.17468334 14.737897 0.46 0.46 -0.17468334+14.737897i
#> displacement Trajectory Simulation TrajSim
#> 1 0.000000000+0.0000000i Traj_2 Sim_7 TrajSim_2_7
#> 2 0.143856590+0.7617846i Traj_2 Sim_7 TrajSim_2_7
#> 3 0.104809374+0.5573607i Traj_2 Sim_7 TrajSim_2_7
#> 4 0.114447622+0.4975039i Traj_2 Sim_7 TrajSim_2_7
#> 5 0.096374389+0.6138621i Traj_2 Sim_7 TrajSim_2_7
#> 6 0.038039073+0.5059451i Traj_2 Sim_7 TrajSim_2_7
#> 7 -0.057641693+0.6315199i Traj_2 Sim_7 TrajSim_2_7
#> 8 0.030322483+0.5905556i Traj_2 Sim_7 TrajSim_2_7
#> 9 0.053052684+0.4925293i Traj_2 Sim_7 TrajSim_2_7
#> 10 0.037033617+0.4702145i Traj_2 Sim_7 TrajSim_2_7
#> 11 -0.045008776+0.6746210i Traj_2 Sim_7 TrajSim_2_7
#> 12 -0.041114388+0.5930372i Traj_2 Sim_7 TrajSim_2_7
#> 13 -0.081129955+0.5158642i Traj_2 Sim_7 TrajSim_2_7
#> 14 -0.005602831+0.6041355i Traj_2 Sim_7 TrajSim_2_7
#> 15 -0.112010952+0.6855929i Traj_2 Sim_7 TrajSim_2_7
#> 16 -0.141631004+0.6366392i Traj_2 Sim_7 TrajSim_2_7
#> 17 -0.123192965+0.5668436i Traj_2 Sim_7 TrajSim_2_7
#> 18 0.012808189+0.7329279i Traj_2 Sim_7 TrajSim_2_7
#> 19 -0.002320190+0.4794922i Traj_2 Sim_7 TrajSim_2_7
#> 20 -0.004981557+0.5639513i Traj_2 Sim_7 TrajSim_2_7
#> 21 -0.102219020+0.4812505i Traj_2 Sim_7 TrajSim_2_7
#> 22 -0.093581822+0.5603868i Traj_2 Sim_7 TrajSim_2_7
#> 23 -0.204069133+0.4713177i Traj_2 Sim_7 TrajSim_2_7
#> 24 -0.126923077+0.4905616i Traj_2 Sim_7 TrajSim_2_7
#>
#>
#> [[8]]
#> [[8]][[1]]
#> x y time displacementTime polar
#> 1 0.6960000 0.946000 0.00 0.00 0.6960000+ 0.946000i
#> 2 0.7246414 1.435770 0.02 0.02 0.7246414+ 1.435770i
#> 3 0.7188927 1.989489 0.04 0.04 0.7188927+ 1.989489i
#> 4 0.7450884 2.432219 0.06 0.06 0.7450884+ 2.432219i
#> 5 0.7828620 2.988646 0.08 0.08 0.7828620+ 2.988646i
#> 6 0.7369216 3.496523 0.10 0.10 0.7369216+ 3.496523i
#> 7 0.7190240 4.031859 0.12 0.12 0.7190240+ 4.031859i
#> 8 0.7275979 4.566377 0.14 0.14 0.7275979+ 4.566377i
#> 9 0.7213656 5.077392 0.16 0.16 0.7213656+ 5.077392i
#> 10 0.7229588 5.599951 0.18 0.18 0.7229588+ 5.599951i
#> 11 0.7412149 6.055748 0.20 0.20 0.7412149+ 6.055748i
#> 12 0.7771605 6.590553 0.22 0.22 0.7771605+ 6.590553i
#> 13 0.8193657 7.158561 0.24 0.24 0.8193657+ 7.158561i
#> 14 0.8790301 7.676651 0.26 0.26 0.8790301+ 7.676651i
#> 15 0.9131456 8.201276 0.28 0.28 0.9131456+ 8.201276i
#> 16 0.9653820 8.800513 0.30 0.30 0.9653820+ 8.800513i
#> 17 0.9843071 9.330974 0.32 0.32 0.9843071+ 9.330974i
#> 18 1.0064115 9.875857 0.34 0.34 1.0064115+ 9.875857i
#> 19 1.0608721 10.406045 0.36 0.36 1.0608721+10.406045i
#> 20 1.1260382 10.994284 0.38 0.38 1.1260382+10.994284i
#> 21 1.2390449 11.548179 0.40 0.40 1.2390449+11.548179i
#> 22 1.3863048 12.079357 0.42 0.42 1.3863048+12.079357i
#> 23 1.5259241 12.604614 0.44 0.44 1.5259241+12.604614i
#> 24 1.6144879 13.077709 0.46 0.46 1.6144879+13.077709i
#> 25 1.7062580 13.526956 0.48 0.48 1.7062580+13.526956i
#> 26 1.7713312 14.040999 0.50 0.50 1.7713312+14.040999i
#> 27 1.8634982 14.539695 0.52 0.52 1.8634982+14.539695i
#> 28 1.9158733 15.044363 0.54 0.54 1.9158733+15.044363i
#> 29 2.0089194 15.492048 0.56 0.56 2.0089194+15.492048i
#> displacement Trajectory Simulation TrajSim
#> 1 0.000000000+0.0000000i Traj_1 Sim_8 TrajSim_1_8
#> 2 0.028641389+0.4897699i Traj_1 Sim_8 TrajSim_1_8
#> 3 -0.005748681+0.5537192i Traj_1 Sim_8 TrajSim_1_8
#> 4 0.026195654+0.4427303i Traj_1 Sim_8 TrajSim_1_8
#> 5 0.037773667+0.5564262i Traj_1 Sim_8 TrajSim_1_8
#> 6 -0.045940452+0.5078778i Traj_1 Sim_8 TrajSim_1_8
#> 7 -0.017897626+0.5353354i Traj_1 Sim_8 TrajSim_1_8
#> 8 0.008573949+0.5345178i Traj_1 Sim_8 TrajSim_1_8
#> 9 -0.006232285+0.5110152i Traj_1 Sim_8 TrajSim_1_8
#> 10 0.001593189+0.5225595i Traj_1 Sim_8 TrajSim_1_8
#> 11 0.018256123+0.4557965i Traj_1 Sim_8 TrajSim_1_8
#> 12 0.035945608+0.5348050i Traj_1 Sim_8 TrajSim_1_8
#> 13 0.042205205+0.5680087i Traj_1 Sim_8 TrajSim_1_8
#> 14 0.059664314+0.5180893i Traj_1 Sim_8 TrajSim_1_8
#> 15 0.034115543+0.5246254i Traj_1 Sim_8 TrajSim_1_8
#> 16 0.052236359+0.5992367i Traj_1 Sim_8 TrajSim_1_8
#> 17 0.018925150+0.5304609i Traj_1 Sim_8 TrajSim_1_8
#> 18 0.022104423+0.5448838i Traj_1 Sim_8 TrajSim_1_8
#> 19 0.054460538+0.5301871i Traj_1 Sim_8 TrajSim_1_8
#> 20 0.065166109+0.5882399i Traj_1 Sim_8 TrajSim_1_8
#> 21 0.113006721+0.5538947i Traj_1 Sim_8 TrajSim_1_8
#> 22 0.147259897+0.5311781i Traj_1 Sim_8 TrajSim_1_8
#> 23 0.139619272+0.5252570i Traj_1 Sim_8 TrajSim_1_8
#> 24 0.088563879+0.4730947i Traj_1 Sim_8 TrajSim_1_8
#> 25 0.091770098+0.4492475i Traj_1 Sim_8 TrajSim_1_8
#> 26 0.065073145+0.5140430i Traj_1 Sim_8 TrajSim_1_8
#> 27 0.092167059+0.4986953i Traj_1 Sim_8 TrajSim_1_8
#> 28 0.052375089+0.5046686i Traj_1 Sim_8 TrajSim_1_8
#> 29 0.093046102+0.4476844i Traj_1 Sim_8 TrajSim_1_8
#>
#> [[8]][[2]]
#> x y time displacementTime polar
#> 1 0.3360000 1.560000 0.00 0.00 0.3360000+ 1.560000i
#> 2 0.2268425 2.147840 0.02 0.02 0.2268425+ 2.147840i
#> 3 0.2238351 2.656484 0.04 0.04 0.2238351+ 2.656484i
#> 4 0.1098080 3.291149 0.06 0.06 0.1098080+ 3.291149i
#> 5 -0.1042477 3.940089 0.08 0.08 -0.1042477+ 3.940089i
#> 6 -0.1858185 4.528903 0.10 0.10 -0.1858185+ 4.528903i
#> 7 -0.3362163 5.212758 0.12 0.12 -0.3362163+ 5.212758i
#> 8 -0.4343398 5.683957 0.14 0.14 -0.4343398+ 5.683957i
#> 9 -0.6049994 6.305955 0.16 0.16 -0.6049994+ 6.305955i
#> 10 -0.7998803 6.948201 0.18 0.18 -0.7998803+ 6.948201i
#> 11 -0.9161271 7.418416 0.20 0.20 -0.9161271+ 7.418416i
#> 12 -1.0906100 7.983891 0.22 0.22 -1.0906100+ 7.983891i
#> 13 -1.2716661 8.535820 0.24 0.24 -1.2716661+ 8.535820i
#> 14 -1.5035183 9.302928 0.26 0.26 -1.5035183+ 9.302928i
#> 15 -1.6990929 9.880498 0.28 0.28 -1.6990929+ 9.880498i
#> 16 -1.8849968 10.568783 0.30 0.30 -1.8849968+10.568783i
#> 17 -1.9985843 11.165522 0.32 0.32 -1.9985843+11.165522i
#> 18 -2.1424320 11.635608 0.34 0.34 -2.1424320+11.635608i
#> 19 -2.4202234 12.330928 0.36 0.36 -2.4202234+12.330928i
#> 20 -2.6808837 12.995852 0.38 0.38 -2.6808837+12.995852i
#> 21 -2.8702536 13.608531 0.40 0.40 -2.8702536+13.608531i
#> 22 -2.9761013 14.172748 0.42 0.42 -2.9761013+14.172748i
#> 23 -3.2093692 14.806291 0.44 0.44 -3.2093692+14.806291i
#> 24 -3.4459907 15.337995 0.46 0.46 -3.4459907+15.337995i
#> displacement Trajectory Simulation TrajSim
#> 1 0.000000000+0.0000000i Traj_2 Sim_8 TrajSim_2_8
#> 2 -0.109157451+0.5878400i Traj_2 Sim_8 TrajSim_2_8
#> 3 -0.003007469+0.5086445i Traj_2 Sim_8 TrajSim_2_8
#> 4 -0.114027126+0.6346644i Traj_2 Sim_8 TrajSim_2_8
#> 5 -0.214055683+0.6489397i Traj_2 Sim_8 TrajSim_2_8
#> 6 -0.081570786+0.5888148i Traj_2 Sim_8 TrajSim_2_8
#> 7 -0.150397792+0.6838551i Traj_2 Sim_8 TrajSim_2_8
#> 8 -0.098123489+0.4711988i Traj_2 Sim_8 TrajSim_2_8
#> 9 -0.170659613+0.6219976i Traj_2 Sim_8 TrajSim_2_8
#> 10 -0.194880883+0.6422457i Traj_2 Sim_8 TrajSim_2_8
#> 11 -0.116246834+0.4702153i Traj_2 Sim_8 TrajSim_2_8
#> 12 -0.174482914+0.5654755i Traj_2 Sim_8 TrajSim_2_8
#> 13 -0.181056014+0.5519284i Traj_2 Sim_8 TrajSim_2_8
#> 14 -0.231852202+0.7671084i Traj_2 Sim_8 TrajSim_2_8
#> 15 -0.195574678+0.5775699i Traj_2 Sim_8 TrajSim_2_8
#> 16 -0.185903850+0.6882847i Traj_2 Sim_8 TrajSim_2_8
#> 17 -0.113587489+0.5967397i Traj_2 Sim_8 TrajSim_2_8
#> 18 -0.143847718+0.4700859i Traj_2 Sim_8 TrajSim_2_8
#> 19 -0.277791451+0.6953197i Traj_2 Sim_8 TrajSim_2_8
#> 20 -0.260660215+0.6649243i Traj_2 Sim_8 TrajSim_2_8
#> 21 -0.189369949+0.6126788i Traj_2 Sim_8 TrajSim_2_8
#> 22 -0.105847729+0.5642172i Traj_2 Sim_8 TrajSim_2_8
#> 23 -0.233267908+0.6335424i Traj_2 Sim_8 TrajSim_2_8
#> 24 -0.236621456+0.5317042i Traj_2 Sim_8 TrajSim_2_8
#>
#>
#> [[9]]
#> [[9]][[1]]
#> x y time displacementTime polar
#> 1 0.6960000 0.946000 0.00 0.00 0.6960000+ 0.946000i
#> 2 0.7461915 1.533973 0.02 0.02 0.7461915+ 1.533973i
#> 3 0.8211387 2.129466 0.04 0.04 0.8211387+ 2.129466i
#> 4 0.9007821 2.576667 0.06 0.06 0.9007821+ 2.576667i
#> 5 1.0109597 3.130258 0.08 0.08 1.0109597+ 3.130258i
#> 6 1.0653776 3.674150 0.10 0.10 1.0653776+ 3.674150i
#> 7 1.1032411 4.166806 0.12 0.12 1.1032411+ 4.166806i
#> 8 1.1362351 4.628338 0.14 0.14 1.1362351+ 4.628338i
#> 9 1.2460765 5.186213 0.16 0.16 1.2460765+ 5.186213i
#> 10 1.3581794 5.696325 0.18 0.18 1.3581794+ 5.696325i
#> 11 1.4990308 6.254784 0.20 0.20 1.4990308+ 6.254784i
#> 12 1.6322862 6.820352 0.22 0.22 1.6322862+ 6.820352i
#> 13 1.7197215 7.424329 0.24 0.24 1.7197215+ 7.424329i
#> 14 1.7950920 7.866332 0.26 0.26 1.7950920+ 7.866332i
#> 15 1.9033023 8.350704 0.28 0.28 1.9033023+ 8.350704i
#> 16 2.0852530 8.853055 0.30 0.30 2.0852530+ 8.853055i
#> 17 2.2607057 9.279982 0.32 0.32 2.2607057+ 9.279982i
#> 18 2.4277364 9.681299 0.34 0.34 2.4277364+ 9.681299i
#> 19 2.6166501 10.112870 0.36 0.36 2.6166501+10.112870i
#> 20 2.8510953 10.593679 0.38 0.38 2.8510953+10.593679i
#> 21 3.1093306 11.050060 0.40 0.40 3.1093306+11.050060i
#> 22 3.3676847 11.453150 0.42 0.42 3.3676847+11.453150i
#> 23 3.7496858 11.993276 0.44 0.44 3.7496858+11.993276i
#> 24 4.0396048 12.465571 0.46 0.46 4.0396048+12.465571i
#> 25 4.3471194 13.023057 0.48 0.48 4.3471194+13.023057i
#> 26 4.5928837 13.433887 0.50 0.50 4.5928837+13.433887i
#> 27 4.8622425 13.849661 0.52 0.52 4.8622425+13.849661i
#> 28 5.0983644 14.334831 0.54 0.54 5.0983644+14.334831i
#> 29 5.3323114 14.771126 0.56 0.56 5.3323114+14.771126i
#> displacement Trajectory Simulation TrajSim
#> 1 0.00000000+0.0000000i Traj_1 Sim_9 TrajSim_1_9
#> 2 0.05019151+0.5879729i Traj_1 Sim_9 TrajSim_1_9
#> 3 0.07494720+0.5954934i Traj_1 Sim_9 TrajSim_1_9
#> 4 0.07964343+0.4472004i Traj_1 Sim_9 TrajSim_1_9
#> 5 0.11017755+0.5535910i Traj_1 Sim_9 TrajSim_1_9
#> 6 0.05441791+0.5438920i Traj_1 Sim_9 TrajSim_1_9
#> 7 0.03786354+0.4926567i Traj_1 Sim_9 TrajSim_1_9
#> 8 0.03299392+0.4615320i Traj_1 Sim_9 TrajSim_1_9
#> 9 0.10984147+0.5578743i Traj_1 Sim_9 TrajSim_1_9
#> 10 0.11210289+0.5101125i Traj_1 Sim_9 TrajSim_1_9
#> 11 0.14085140+0.5584584i Traj_1 Sim_9 TrajSim_1_9
#> 12 0.13325538+0.5655681i Traj_1 Sim_9 TrajSim_1_9
#> 13 0.08743528+0.6039772i Traj_1 Sim_9 TrajSim_1_9
#> 14 0.07537054+0.4420030i Traj_1 Sim_9 TrajSim_1_9
#> 15 0.10821023+0.4843725i Traj_1 Sim_9 TrajSim_1_9
#> 16 0.18195077+0.5023503i Traj_1 Sim_9 TrajSim_1_9
#> 17 0.17545267+0.4269278i Traj_1 Sim_9 TrajSim_1_9
#> 18 0.16703066+0.4013167i Traj_1 Sim_9 TrajSim_1_9
#> 19 0.18891375+0.4315708i Traj_1 Sim_9 TrajSim_1_9
#> 20 0.23444515+0.4808091i Traj_1 Sim_9 TrajSim_1_9
#> 21 0.25823538+0.4563815i Traj_1 Sim_9 TrajSim_1_9
#> 22 0.25835410+0.4030895i Traj_1 Sim_9 TrajSim_1_9
#> 23 0.38200110+0.5401258i Traj_1 Sim_9 TrajSim_1_9
#> 24 0.28991896+0.4722949i Traj_1 Sim_9 TrajSim_1_9
#> 25 0.30751455+0.5574860i Traj_1 Sim_9 TrajSim_1_9
#> 26 0.24576436+0.4108300i Traj_1 Sim_9 TrajSim_1_9
#> 27 0.26935882+0.4157746i Traj_1 Sim_9 TrajSim_1_9
#> 28 0.23612183+0.4851696i Traj_1 Sim_9 TrajSim_1_9
#> 29 0.23394703+0.4362954i Traj_1 Sim_9 TrajSim_1_9
#>
#> [[9]][[2]]
#> x y time displacementTime polar
#> 1 0.3360000 1.560000 0.00 0.00 0.3360000+ 1.560000i
#> 2 0.3536214 2.015660 0.02 0.02 0.3536214+ 2.015660i
#> 3 0.4442176 2.538865 0.04 0.04 0.4442176+ 2.538865i
#> 4 0.5006001 3.095130 0.06 0.06 0.5006001+ 3.095130i
#> 5 0.6468223 3.717706 0.08 0.08 0.6468223+ 3.717706i
#> 6 0.7814448 4.344439 0.10 0.10 0.7814448+ 4.344439i
#> 7 0.9478916 4.849324 0.12 0.12 0.9478916+ 4.849324i
#> 8 1.1420155 5.390110 0.14 0.14 1.1420155+ 5.390110i
#> 9 1.4661936 5.909848 0.16 0.16 1.4661936+ 5.909848i
#> 10 1.8571784 6.412265 0.18 0.18 1.8571784+ 6.412265i
#> 11 2.2472542 6.962001 0.20 0.20 2.2472542+ 6.962001i
#> 12 2.6426731 7.338352 0.22 0.22 2.6426731+ 7.338352i
#> 13 3.0995469 7.791796 0.24 0.24 3.0995469+ 7.791796i
#> 14 3.6371314 8.191771 0.26 0.26 3.6371314+ 8.191771i
#> 15 4.1311068 8.533403 0.28 0.28 4.1311068+ 8.533403i
#> 16 4.5521767 8.981956 0.30 0.30 4.5521767+ 8.981956i
#> 17 4.9778634 9.332069 0.32 0.32 4.9778634+ 9.332069i
#> 18 5.5363103 9.713476 0.34 0.34 5.5363103+ 9.713476i
#> 19 6.0685183 9.993185 0.36 0.36 6.0685183+ 9.993185i
#> 20 6.6217230 10.292866 0.38 0.38 6.6217230+10.292866i
#> 21 7.1500426 10.657413 0.40 0.40 7.1500426+10.657413i
#> 22 7.6665759 11.050756 0.42 0.42 7.6665759+11.050756i
#> 23 8.1819379 11.369634 0.44 0.44 8.1819379+11.369634i
#> 24 8.7551185 11.654117 0.46 0.46 8.7551185+11.654117i
#> displacement Trajectory Simulation TrajSim
#> 1 0.00000000+0.0000000i Traj_2 Sim_9 TrajSim_2_9
#> 2 0.01762136+0.4556595i Traj_2 Sim_9 TrajSim_2_9
#> 3 0.09059629+0.5232053i Traj_2 Sim_9 TrajSim_2_9
#> 4 0.05638248+0.5562656i Traj_2 Sim_9 TrajSim_2_9
#> 5 0.14622220+0.6225756i Traj_2 Sim_9 TrajSim_2_9
#> 6 0.13462250+0.6267333i Traj_2 Sim_9 TrajSim_2_9
#> 7 0.16644674+0.5048843i Traj_2 Sim_9 TrajSim_2_9
#> 8 0.19412393+0.5407866i Traj_2 Sim_9 TrajSim_2_9
#> 9 0.32417809+0.5197375i Traj_2 Sim_9 TrajSim_2_9
#> 10 0.39098483+0.5024171i Traj_2 Sim_9 TrajSim_2_9
#> 11 0.39007578+0.5497362i Traj_2 Sim_9 TrajSim_2_9
#> 12 0.39541893+0.3763509i Traj_2 Sim_9 TrajSim_2_9
#> 13 0.45687375+0.4534442i Traj_2 Sim_9 TrajSim_2_9
#> 14 0.53758449+0.3999751i Traj_2 Sim_9 TrajSim_2_9
#> 15 0.49397547+0.3416322i Traj_2 Sim_9 TrajSim_2_9
#> 16 0.42106985+0.4485527i Traj_2 Sim_9 TrajSim_2_9
#> 17 0.42568668+0.3501129i Traj_2 Sim_9 TrajSim_2_9
#> 18 0.55844697+0.3814073i Traj_2 Sim_9 TrajSim_2_9
#> 19 0.53220798+0.2797084i Traj_2 Sim_9 TrajSim_2_9
#> 20 0.55320469+0.2996817i Traj_2 Sim_9 TrajSim_2_9
#> 21 0.52831963+0.3645464i Traj_2 Sim_9 TrajSim_2_9
#> 22 0.51653323+0.3933432i Traj_2 Sim_9 TrajSim_2_9
#> 23 0.51536204+0.3188776i Traj_2 Sim_9 TrajSim_2_9
#> 24 0.57318062+0.2844834i Traj_2 Sim_9 TrajSim_2_9
#>
#>
#> [[10]]
#> [[10]][[1]]
#> x y time displacementTime polar
#> 1 0.6960000 0.946000 0.00 0.00 0.6960000+ 0.946000i
#> 2 0.7848537 1.532360 0.02 0.02 0.7848537+ 1.532360i
#> 3 0.8604024 1.999808 0.04 0.04 0.8604024+ 1.999808i
#> 4 0.8857582 2.499092 0.06 0.06 0.8857582+ 2.499092i
#> 5 0.8744539 3.046934 0.08 0.08 0.8744539+ 3.046934i
#> 6 0.8649236 3.526255 0.10 0.10 0.8649236+ 3.526255i
#> 7 0.8346074 4.047256 0.12 0.12 0.8346074+ 4.047256i
#> 8 0.8351089 4.506916 0.14 0.14 0.8351089+ 4.506916i
#> 9 0.8070763 5.032186 0.16 0.16 0.8070763+ 5.032186i
#> 10 0.7824454 5.560598 0.18 0.18 0.7824454+ 5.560598i
#> 11 0.7418469 6.073970 0.20 0.20 0.7418469+ 6.073970i
#> 12 0.7474811 6.560688 0.22 0.22 0.7474811+ 6.560688i
#> 13 0.7447616 7.103925 0.24 0.24 0.7447616+ 7.103925i
#> 14 0.7487505 7.683520 0.26 0.26 0.7487505+ 7.683520i
#> 15 0.7680659 8.147340 0.28 0.28 0.7680659+ 8.147340i
#> 16 0.7781649 8.621901 0.30 0.30 0.7781649+ 8.621901i
#> 17 0.7503747 9.133744 0.32 0.32 0.7503747+ 9.133744i
#> 18 0.7459324 9.676611 0.34 0.34 0.7459324+ 9.676611i
#> 19 0.7308739 10.210355 0.36 0.36 0.7308739+10.210355i
#> 20 0.7527914 10.694673 0.38 0.38 0.7527914+10.694673i
#> 21 0.7731415 11.260598 0.40 0.40 0.7731415+11.260598i
#> 22 0.7805479 11.833838 0.42 0.42 0.7805479+11.833838i
#> 23 0.8436642 12.309068 0.44 0.44 0.8436642+12.309068i
#> 24 0.9455952 12.779038 0.46 0.46 0.9455952+12.779038i
#> 25 1.0929853 13.208944 0.48 0.48 1.0929853+13.208944i
#> 26 1.2489502 13.645585 0.50 0.50 1.2489502+13.645585i
#> 27 1.4183254 14.103904 0.52 0.52 1.4183254+14.103904i
#> 28 1.5869816 14.624798 0.54 0.54 1.5869816+14.624798i
#> 29 1.7509218 15.076926 0.56 0.56 1.7509218+15.076926i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000000+0.0000000i Traj_1 Sim_10 TrajSim_1_10
#> 2 0.0888536980+0.5863599i Traj_1 Sim_10 TrajSim_1_10
#> 3 0.0755487213+0.4674476i Traj_1 Sim_10 TrajSim_1_10
#> 4 0.0253557922+0.4992843i Traj_1 Sim_10 TrajSim_1_10
#> 5 -0.0113042779+0.5478426i Traj_1 Sim_10 TrajSim_1_10
#> 6 -0.0095303697+0.4793208i Traj_1 Sim_10 TrajSim_1_10
#> 7 -0.0303161697+0.5210007i Traj_1 Sim_10 TrajSim_1_10
#> 8 0.0005015385+0.4596604i Traj_1 Sim_10 TrajSim_1_10
#> 9 -0.0280325894+0.5252693i Traj_1 Sim_10 TrajSim_1_10
#> 10 -0.0246309735+0.5284127i Traj_1 Sim_10 TrajSim_1_10
#> 11 -0.0405984714+0.5133719i Traj_1 Sim_10 TrajSim_1_10
#> 12 0.0056341842+0.4867183i Traj_1 Sim_10 TrajSim_1_10
#> 13 -0.0027195177+0.5432362i Traj_1 Sim_10 TrajSim_1_10
#> 14 0.0039888971+0.5795953i Traj_1 Sim_10 TrajSim_1_10
#> 15 0.0193154178+0.4638203i Traj_1 Sim_10 TrajSim_1_10
#> 16 0.0100990506+0.4745608i Traj_1 Sim_10 TrajSim_1_10
#> 17 -0.0277901908+0.5118426i Traj_1 Sim_10 TrajSim_1_10
#> 18 -0.0044423384+0.5428674i Traj_1 Sim_10 TrajSim_1_10
#> 19 -0.0150585320+0.5337437i Traj_1 Sim_10 TrajSim_1_10
#> 20 0.0219175426+0.4843185i Traj_1 Sim_10 TrajSim_1_10
#> 21 0.0203500968+0.5659245i Traj_1 Sim_10 TrajSim_1_10
#> 22 0.0074063533+0.5732405i Traj_1 Sim_10 TrajSim_1_10
#> 23 0.0631163329+0.4752294i Traj_1 Sim_10 TrajSim_1_10
#> 24 0.1019310263+0.4699698i Traj_1 Sim_10 TrajSim_1_10
#> 25 0.1473901192+0.4299066i Traj_1 Sim_10 TrajSim_1_10
#> 26 0.1559648770+0.4366412i Traj_1 Sim_10 TrajSim_1_10
#> 27 0.1693751839+0.4583188i Traj_1 Sim_10 TrajSim_1_10
#> 28 0.1686561773+0.5208939i Traj_1 Sim_10 TrajSim_1_10
#> 29 0.1639401974+0.4521281i Traj_1 Sim_10 TrajSim_1_10
#>
#> [[10]][[2]]
#> x y time displacementTime polar
#> 1 0.3360000 1.560000 0.00 0.00 0.3360000+ 1.560000i
#> 2 0.3489061 2.271035 0.02 0.02 0.3489061+ 2.271035i
#> 3 0.6246042 2.850510 0.04 0.04 0.6246042+ 2.850510i
#> 4 0.9297149 3.498689 0.06 0.06 0.9297149+ 3.498689i
#> 5 1.0799601 4.131317 0.08 0.08 1.0799601+ 4.131317i
#> 6 1.1918252 4.642631 0.10 0.10 1.1918252+ 4.642631i
#> 7 1.3708628 5.436183 0.12 0.12 1.3708628+ 5.436183i
#> 8 1.5228901 5.967880 0.14 0.14 1.5228901+ 5.967880i
#> 9 1.7121769 6.450473 0.16 0.16 1.7121769+ 6.450473i
#> 10 1.9268254 7.135985 0.18 0.18 1.9268254+ 7.135985i
#> 11 2.2309889 7.755097 0.20 0.20 2.2309889+ 7.755097i
#> 12 2.5004172 8.307194 0.22 0.22 2.5004172+ 8.307194i
#> 13 2.7895553 8.937548 0.24 0.24 2.7895553+ 8.937548i
#> 14 2.8767115 9.560505 0.26 0.26 2.8767115+ 9.560505i
#> 15 3.0113441 10.206354 0.28 0.28 3.0113441+10.206354i
#> 16 3.1436510 10.686793 0.30 0.30 3.1436510+10.686793i
#> 17 3.4471406 11.178313 0.32 0.32 3.4471406+11.178313i
#> 18 3.7329867 11.551063 0.34 0.34 3.7329867+11.551063i
#> 19 4.1532611 11.963720 0.36 0.36 4.1532611+11.963720i
#> 20 4.5667006 12.381158 0.38 0.38 4.5667006+12.381158i
#> 21 5.0208624 12.770158 0.40 0.40 5.0208624+12.770158i
#> 22 5.4236039 13.129003 0.42 0.42 5.4236039+13.129003i
#> 23 5.8334029 13.539848 0.44 0.44 5.8334029+13.539848i
#> 24 6.3220860 13.985934 0.46 0.46 6.3220860+13.985934i
#> displacement Trajectory Simulation TrajSim
#> 1 0.00000000+0.0000000i Traj_2 Sim_10 TrajSim_2_10
#> 2 0.01290612+0.7110347i Traj_2 Sim_10 TrajSim_2_10
#> 3 0.27569803+0.5794754i Traj_2 Sim_10 TrajSim_2_10
#> 4 0.30511076+0.6481789i Traj_2 Sim_10 TrajSim_2_10
#> 5 0.15024516+0.6326279i Traj_2 Sim_10 TrajSim_2_10
#> 6 0.11186508+0.5113138i Traj_2 Sim_10 TrajSim_2_10
#> 7 0.17903767+0.7935526i Traj_2 Sim_10 TrajSim_2_10
#> 8 0.15202729+0.5316971i Traj_2 Sim_10 TrajSim_2_10
#> 9 0.18928675+0.4825921i Traj_2 Sim_10 TrajSim_2_10
#> 10 0.21464854+0.6855128i Traj_2 Sim_10 TrajSim_2_10
#> 11 0.30416347+0.6191116i Traj_2 Sim_10 TrajSim_2_10
#> 12 0.26942836+0.5520968i Traj_2 Sim_10 TrajSim_2_10
#> 13 0.28913802+0.6303541i Traj_2 Sim_10 TrajSim_2_10
#> 14 0.08715625+0.6229573i Traj_2 Sim_10 TrajSim_2_10
#> 15 0.13463257+0.6458488i Traj_2 Sim_10 TrajSim_2_10
#> 16 0.13230693+0.4804389i Traj_2 Sim_10 TrajSim_2_10
#> 17 0.30348962+0.4915201i Traj_2 Sim_10 TrajSim_2_10
#> 18 0.28584603+0.3727502i Traj_2 Sim_10 TrajSim_2_10
#> 19 0.42027441+0.4126567i Traj_2 Sim_10 TrajSim_2_10
#> 20 0.41343950+0.4174384i Traj_2 Sim_10 TrajSim_2_10
#> 21 0.45416188+0.3889999i Traj_2 Sim_10 TrajSim_2_10
#> 22 0.40274149+0.3588452i Traj_2 Sim_10 TrajSim_2_10
#> 23 0.40979898+0.4108445i Traj_2 Sim_10 TrajSim_2_10
#> 24 0.48868304+0.4460861i Traj_2 Sim_10 TrajSim_2_10
sim_unconstrained_mount <- simulate_track(sbMountTom, nsim = 100, model = "Unconstrained")
print(sim_unconstrained_mount[1:10])#> [[1]]
#> [[1]][[1]]
#> x y time displacementTime polar
#> 1 36.88200 14.05600 0.00 0.00 36.88200+14.05600i
#> 2 37.44137 14.72384 0.02 0.02 37.44137+14.72384i
#> 3 38.02965 15.32431 0.04 0.04 38.02965+15.32431i
#> 4 38.56012 15.92318 0.06 0.06 38.56012+15.92318i
#> 5 39.12622 16.67384 0.08 0.08 39.12622+16.67384i
#> 6 39.70698 17.36664 0.10 0.10 39.70698+17.36664i
#> 7 40.32668 17.99331 0.12 0.12 40.32668+17.99331i
#> 8 40.90511 18.54416 0.14 0.14 40.90511+18.54416i
#> 9 41.46633 19.18488 0.16 0.16 41.46633+19.18488i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_1 Sim_1 TrajSim_1_1
#> 2 0.5593695+0.6678379i Traj_1 Sim_1 TrajSim_1_1
#> 3 0.5882854+0.6004748i Traj_1 Sim_1 TrajSim_1_1
#> 4 0.5304650+0.5988624i Traj_1 Sim_1 TrajSim_1_1
#> 5 0.5660994+0.7506626i Traj_1 Sim_1 TrajSim_1_1
#> 6 0.5807657+0.6928013i Traj_1 Sim_1 TrajSim_1_1
#> 7 0.6196906+0.6266729i Traj_1 Sim_1 TrajSim_1_1
#> 8 0.5784321+0.5508517i Traj_1 Sim_1 TrajSim_1_1
#> 9 0.5612206+0.6407144i Traj_1 Sim_1 TrajSim_1_1
#>
#> [[1]][[2]]
#> x y time displacementTime polar
#> 1 35.53200 13.516000 0.00 0.00 35.53200+13.516000i
#> 2 35.27432 12.572514 0.02 0.02 35.27432+12.572514i
#> 3 34.90562 11.688432 0.04 0.04 34.90562+11.688432i
#> 4 34.66248 10.846164 0.06 0.06 34.66248+10.846164i
#> 5 34.27151 9.903986 0.08 0.08 34.27151+ 9.903986i
#> 6 33.95426 9.055041 0.10 0.10 33.95426+ 9.055041i
#> 7 33.75676 7.920782 0.12 0.12 33.75676+ 7.920782i
#> 8 33.62028 7.079310 0.14 0.14 33.62028+ 7.079310i
#> 9 33.39168 6.131146 0.16 0.16 33.39168+ 6.131146i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_2 Sim_1 TrajSim_2_1
#> 2 -0.2576751-0.9434862i Traj_2 Sim_1 TrajSim_2_1
#> 3 -0.3687077-0.8840815i Traj_2 Sim_1 TrajSim_2_1
#> 4 -0.2431360-0.8422683i Traj_2 Sim_1 TrajSim_2_1
#> 5 -0.3909679-0.9421780i Traj_2 Sim_1 TrajSim_2_1
#> 6 -0.3172523-0.8489453i Traj_2 Sim_1 TrajSim_2_1
#> 7 -0.1975048-1.1342593i Traj_2 Sim_1 TrajSim_2_1
#> 8 -0.1364736-0.8414716i Traj_2 Sim_1 TrajSim_2_1
#> 9 -0.2286005-0.9481642i Traj_2 Sim_1 TrajSim_2_1
#>
#> [[1]][[3]]
#> x y time displacementTime polar
#> 1 34.54800 14.10000 0.00 0.00 34.54800+14.10000i
#> 2 35.74647 14.21720 0.02 0.02 35.74647+14.21720i
#> 3 36.85404 14.24744 0.04 0.04 36.85404+14.24744i
#> 4 37.97134 14.31477 0.06 0.06 37.97134+14.31477i
#> 5 38.99374 14.36186 0.08 0.08 38.99374+14.36186i
#> displacement Trajectory Simulation TrajSim
#> 1 0.000000+0.00000000i Traj_3 Sim_1 TrajSim_3_1
#> 2 1.198472+0.11719993i Traj_3 Sim_1 TrajSim_3_1
#> 3 1.107571+0.03024281i Traj_3 Sim_1 TrajSim_3_1
#> 4 1.117300+0.06732390i Traj_3 Sim_1 TrajSim_3_1
#> 5 1.022402+0.04709200i Traj_3 Sim_1 TrajSim_3_1
#>
#> [[1]][[4]]
#> x y time displacementTime polar
#> 1 32.26000 14.51800 0.00 0.00 32.26000+14.51800i
#> 2 31.55112 13.90513 0.02 0.02 31.55112+13.90513i
#> 3 30.83129 13.20112 0.04 0.04 30.83129+13.20112i
#> 4 30.09769 12.29322 0.06 0.06 30.09769+12.29322i
#> 5 29.47640 11.51888 0.08 0.08 29.47640+11.51888i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_4 Sim_1 TrajSim_4_1
#> 2 -0.7088819-0.6128665i Traj_4 Sim_1 TrajSim_4_1
#> 3 -0.7198307-0.7040161i Traj_4 Sim_1 TrajSim_4_1
#> 4 -0.7335933-0.9078991i Traj_4 Sim_1 TrajSim_4_1
#> 5 -0.6212945-0.7743371i Traj_4 Sim_1 TrajSim_4_1
#>
#> [[1]][[5]]
#> x y time displacementTime polar
#> 1 28.29000 13.57800 0.00 0.00 28.29000+13.57800i
#> 2 27.54452 13.34965 0.02 0.02 27.54452+13.34965i
#> 3 26.85172 12.99172 0.04 0.04 26.85172+12.99172i
#> 4 26.25083 12.69327 0.06 0.06 26.25083+12.69327i
#> 5 25.43619 12.49815 0.08 0.08 25.43619+12.49815i
#> 6 24.81965 12.45908 0.10 0.10 24.81965+12.45908i
#> 7 24.05265 12.55181 0.12 0.12 24.05265+12.55181i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.00000000i Traj_5 Sim_1 TrajSim_5_1
#> 2 -0.7454839-0.22834646i Traj_5 Sim_1 TrajSim_5_1
#> 3 -0.6927939-0.35793148i Traj_5 Sim_1 TrajSim_5_1
#> 4 -0.6008953-0.29845682i Traj_5 Sim_1 TrajSim_5_1
#> 5 -0.8146332-0.19511757i Traj_5 Sim_1 TrajSim_5_1
#> 6 -0.6165452-0.03906289i Traj_5 Sim_1 TrajSim_5_1
#> 7 -0.7669950+0.09272136i Traj_5 Sim_1 TrajSim_5_1
#>
#> [[1]][[6]]
#> x y time displacementTime polar
#> 1 26.19800 13.698000 0.00 0.00 26.19800+13.698000i
#> 2 26.35874 12.716991 0.02 0.02 26.35874+12.716991i
#> 3 26.51271 11.624664 0.04 0.04 26.51271+11.624664i
#> 4 26.55374 10.524924 0.06 0.06 26.55374+10.524924i
#> 5 26.60793 9.470244 0.08 0.08 26.60793+ 9.470244i
#> 6 26.67775 8.287875 0.10 0.10 26.67775+ 8.287875i
#> displacement Trajectory Simulation TrajSim
#> 1 0.00000000+0.000000i Traj_6 Sim_1 TrajSim_6_1
#> 2 0.16074318-0.981009i Traj_6 Sim_1 TrajSim_6_1
#> 3 0.15396967-1.092327i Traj_6 Sim_1 TrajSim_6_1
#> 4 0.04102889-1.099740i Traj_6 Sim_1 TrajSim_6_1
#> 5 0.05419141-1.054680i Traj_6 Sim_1 TrajSim_6_1
#> 6 0.06981539-1.182369i Traj_6 Sim_1 TrajSim_6_1
#>
#> [[1]][[7]]
#> x y time displacementTime polar
#> 1 26.47200 15.49600 0.00 0.00 26.47200+15.49600i
#> 2 27.15567 14.50193 0.02 0.02 27.15567+14.50193i
#> 3 28.01387 13.39648 0.04 0.04 28.01387+13.39648i
#> 4 28.89236 12.31885 0.06 0.06 28.89236+12.31885i
#> 5 29.75393 11.27890 0.08 0.08 29.75393+11.27890i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_7 Sim_1 TrajSim_7_1
#> 2 0.6836709-0.9940693i Traj_7 Sim_1 TrajSim_7_1
#> 3 0.8581960-1.1054459i Traj_7 Sim_1 TrajSim_7_1
#> 4 0.8784882-1.0776325i Traj_7 Sim_1 TrajSim_7_1
#> 5 0.8615780-1.0399528i Traj_7 Sim_1 TrajSim_7_1
#>
#> [[1]][[8]]
#> x y time displacementTime polar
#> 1 13.21800 8.752000 0.00 0.00 13.21800+8.752000i
#> 2 12.82259 8.553522 0.02 0.02 12.82259+8.553522i
#> 3 12.55916 8.203138 0.04 0.04 12.55916+8.203138i
#> 4 12.32479 7.848452 0.06 0.06 12.32479+7.848452i
#> 5 12.02901 7.507400 0.08 0.08 12.02901+7.507400i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_8 Sim_1 TrajSim_8_1
#> 2 -0.3954074-0.1984782i Traj_8 Sim_1 TrajSim_8_1
#> 3 -0.2634311-0.3503834i Traj_8 Sim_1 TrajSim_8_1
#> 4 -0.2343751-0.3546859i Traj_8 Sim_1 TrajSim_8_1
#> 5 -0.2957782-0.3410523i Traj_8 Sim_1 TrajSim_8_1
#>
#> [[1]][[9]]
#> x y time displacementTime polar
#> 1 15.63800 8.164000 0.00 0.00 15.63800+ 8.164000i
#> 2 15.41558 9.276267 0.02 0.02 15.41558+ 9.276267i
#> 3 15.44395 10.177253 0.04 0.04 15.44395+10.177253i
#> 4 15.47761 11.124837 0.06 0.06 15.47761+11.124837i
#> 5 15.45204 12.146102 0.08 0.08 15.45204+12.146102i
#> displacement Trajectory Simulation TrajSim
#> 1 0.00000000+0.0000000i Traj_9 Sim_1 TrajSim_9_1
#> 2 -0.22242432+1.1122665i Traj_9 Sim_1 TrajSim_9_1
#> 3 0.02837331+0.9009865i Traj_9 Sim_1 TrajSim_9_1
#> 4 0.03366473+0.9475836i Traj_9 Sim_1 TrajSim_9_1
#> 5 -0.02557102+1.0212658i Traj_9 Sim_1 TrajSim_9_1
#>
#> [[1]][[10]]
#> x y time displacementTime polar
#> 1 14.69800 6.798000 0.00 0.00 14.69800+ 6.798000i
#> 2 15.05720 7.651238 0.02 0.02 15.05720+ 7.651238i
#> 3 15.29174 8.524267 0.04 0.04 15.29174+ 8.524267i
#> 4 15.51485 9.320580 0.06 0.06 15.51485+ 9.320580i
#> 5 15.77822 10.161906 0.08 0.08 15.77822+10.161906i
#> 6 15.97901 11.045131 0.10 0.10 15.97901+11.045131i
#> 7 16.19204 11.938061 0.12 0.12 16.19204+11.938061i
#> 8 16.41597 12.769373 0.14 0.14 16.41597+12.769373i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_10 Sim_1 TrajSim_10_1
#> 2 0.3591965+0.8532378i Traj_10 Sim_1 TrajSim_10_1
#> 3 0.2345426+0.8730293i Traj_10 Sim_1 TrajSim_10_1
#> 4 0.2231066+0.7963128i Traj_10 Sim_1 TrajSim_10_1
#> 5 0.2633778+0.8413260i Traj_10 Sim_1 TrajSim_10_1
#> 6 0.2007898+0.8832251i Traj_10 Sim_1 TrajSim_10_1
#> 7 0.2130280+0.8929295i Traj_10 Sim_1 TrajSim_10_1
#> 8 0.2239282+0.8313129i Traj_10 Sim_1 TrajSim_10_1
#>
#> [[1]][[11]]
#> x y time displacementTime polar
#> 1 12.006000 7.316000 0.00 0.00 12.006000+7.316000i
#> 2 11.043471 7.092651 0.02 0.02 11.043471+7.092651i
#> 3 9.984614 6.814571 0.04 0.04 9.984614+6.814571i
#> 4 9.116702 6.555071 0.06 0.06 9.116702+6.555071i
#> 5 8.046175 6.235099 0.08 0.08 8.046175+6.235099i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_11 Sim_1 TrajSim_11_1
#> 2 -0.9625289-0.2233485i Traj_11 Sim_1 TrajSim_11_1
#> 3 -1.0588570-0.2780801i Traj_11 Sim_1 TrajSim_11_1
#> 4 -0.8679124-0.2594999i Traj_11 Sim_1 TrajSim_11_1
#> 5 -1.0705262-0.3199723i Traj_11 Sim_1 TrajSim_11_1
#>
#>
#> [[2]]
#> [[2]][[1]]
#> x y time displacementTime polar
#> 1 36.88200 14.056000 0.00 0.00 36.88200+14.056000i
#> 2 37.04717 13.199773 0.02 0.02 37.04717+13.199773i
#> 3 37.02886 12.333452 0.04 0.04 37.02886+12.333452i
#> 4 37.06121 11.343139 0.06 0.06 37.06121+11.343139i
#> 5 37.18862 10.456821 0.08 0.08 37.18862+10.456821i
#> 6 37.29597 9.582477 0.10 0.10 37.29597+ 9.582477i
#> 7 37.44050 8.806193 0.12 0.12 37.44050+ 8.806193i
#> 8 37.56054 7.905794 0.14 0.14 37.56054+ 7.905794i
#> 9 37.57095 6.934409 0.16 0.16 37.57095+ 6.934409i
#> displacement Trajectory Simulation TrajSim
#> 1 0.00000000+0.0000000i Traj_1 Sim_2 TrajSim_1_2
#> 2 0.16517409-0.8562272i Traj_1 Sim_2 TrajSim_1_2
#> 3 -0.01830911-0.8663203i Traj_1 Sim_2 TrajSim_1_2
#> 4 0.03234296-0.9903133i Traj_1 Sim_2 TrajSim_1_2
#> 5 0.12741533-0.8863181i Traj_1 Sim_2 TrajSim_1_2
#> 6 0.10734239-0.8743440i Traj_1 Sim_2 TrajSim_1_2
#> 7 0.14453716-0.7762840i Traj_1 Sim_2 TrajSim_1_2
#> 8 0.12003714-0.9003992i Traj_1 Sim_2 TrajSim_1_2
#> 9 0.01040999-0.9713846i Traj_1 Sim_2 TrajSim_1_2
#>
#> [[2]][[2]]
#> x y time displacementTime polar
#> 1 35.53200 13.51600 0.00 0.00 35.53200+13.51600i
#> 2 34.67517 13.54908 0.02 0.02 34.67517+13.54908i
#> 3 33.65140 13.63511 0.04 0.04 33.65140+13.63511i
#> 4 32.70154 13.80762 0.06 0.06 32.70154+13.80762i
#> 5 31.72154 13.91831 0.08 0.08 31.72154+13.91831i
#> 6 30.75317 14.15704 0.10 0.10 30.75317+14.15704i
#> 7 29.69256 14.39580 0.12 0.12 29.69256+14.39580i
#> 8 28.85922 14.56171 0.14 0.14 28.85922+14.56171i
#> 9 27.98055 14.85609 0.16 0.16 27.98055+14.85609i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.00000000i Traj_2 Sim_2 TrajSim_2_2
#> 2 -0.8568280+0.03307961i Traj_2 Sim_2 TrajSim_2_2
#> 3 -1.0237736+0.08603303i Traj_2 Sim_2 TrajSim_2_2
#> 4 -0.9498579+0.17251122i Traj_2 Sim_2 TrajSim_2_2
#> 5 -0.9799965+0.11068274i Traj_2 Sim_2 TrajSim_2_2
#> 6 -0.9683750+0.23873662i Traj_2 Sim_2 TrajSim_2_2
#> 7 -1.0606106+0.23875897i Traj_2 Sim_2 TrajSim_2_2
#> 8 -0.8333365+0.16590959i Traj_2 Sim_2 TrajSim_2_2
#> 9 -0.8786709+0.29437486i Traj_2 Sim_2 TrajSim_2_2
#>
#> [[2]][[3]]
#> x y time displacementTime polar
#> 1 34.54800 14.10000 0.00 0.00 34.54800+14.10000i
#> 2 35.25638 13.25442 0.02 0.02 35.25638+13.25442i
#> 3 36.00202 12.37550 0.04 0.04 36.00202+12.37550i
#> 4 36.72149 11.57834 0.06 0.06 36.72149+11.57834i
#> 5 37.46527 10.72604 0.08 0.08 37.46527+10.72604i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_3 Sim_2 TrajSim_3_2
#> 2 0.7083803-0.8455812i Traj_3 Sim_2 TrajSim_3_2
#> 3 0.7456365-0.8789148i Traj_3 Sim_2 TrajSim_3_2
#> 4 0.7194743-0.7971689i Traj_3 Sim_2 TrajSim_3_2
#> 5 0.7437774-0.8522933i Traj_3 Sim_2 TrajSim_3_2
#>
#> [[2]][[4]]
#> x y time displacementTime polar
#> 1 32.26000 14.51800 0.00 0.00 32.26000+14.51800i
#> 2 32.41720 15.56661 0.02 0.02 32.41720+15.56661i
#> 3 32.33068 16.60815 0.04 0.04 32.33068+16.60815i
#> 4 32.21958 17.65522 0.06 0.06 32.21958+17.65522i
#> 5 32.00103 18.76203 0.08 0.08 32.00103+18.76203i
#> displacement Trajectory Simulation TrajSim
#> 1 0.00000000+0.000000i Traj_4 Sim_2 TrajSim_4_2
#> 2 0.15719559+1.048612i Traj_4 Sim_2 TrajSim_4_2
#> 3 -0.08651449+1.041536i Traj_4 Sim_2 TrajSim_4_2
#> 4 -0.11110492+1.047076i Traj_4 Sim_2 TrajSim_4_2
#> 5 -0.21854781+1.106809i Traj_4 Sim_2 TrajSim_4_2
#>
#> [[2]][[5]]
#> x y time displacementTime polar
#> 1 28.29000 13.578000 0.00 0.00 28.29000+13.578000i
#> 2 28.29335 12.887641 0.02 0.02 28.29335+12.887641i
#> 3 28.25191 12.065675 0.04 0.04 28.25191+12.065675i
#> 4 28.31261 11.442289 0.06 0.06 28.31261+11.442289i
#> 5 28.31767 10.928169 0.08 0.08 28.31767+10.928169i
#> 6 28.38790 10.332098 0.10 0.10 28.38790+10.332098i
#> 7 28.37025 9.516189 0.12 0.12 28.37025+ 9.516189i
#> displacement Trajectory Simulation TrajSim
#> 1 0.000000000+0.0000000i Traj_5 Sim_2 TrajSim_5_2
#> 2 0.003349673-0.6903587i Traj_5 Sim_2 TrajSim_5_2
#> 3 -0.041443427-0.8219661i Traj_5 Sim_2 TrajSim_5_2
#> 4 0.060703804-0.6233862i Traj_5 Sim_2 TrajSim_5_2
#> 5 0.005064538-0.5141205i Traj_5 Sim_2 TrajSim_5_2
#> 6 0.070228517-0.5960706i Traj_5 Sim_2 TrajSim_5_2
#> 7 -0.017652371-0.8159093i Traj_5 Sim_2 TrajSim_5_2
#>
#> [[2]][[6]]
#> x y time displacementTime polar
#> 1 26.19800 13.69800 0.00 0.00 26.19800+13.69800i
#> 2 25.65774 14.73067 0.02 0.02 25.65774+14.73067i
#> 3 25.26191 15.79430 0.04 0.04 25.26191+15.79430i
#> 4 24.82036 16.76289 0.06 0.06 24.82036+16.76289i
#> 5 24.42763 17.60281 0.08 0.08 24.42763+17.60281i
#> 6 23.95699 18.49446 0.10 0.10 23.95699+18.49446i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_6 Sim_2 TrajSim_6_2
#> 2 -0.5402563+1.0326675i Traj_6 Sim_2 TrajSim_6_2
#> 3 -0.3958347+1.0636345i Traj_6 Sim_2 TrajSim_6_2
#> 4 -0.4415488+0.9685922i Traj_6 Sim_2 TrajSim_6_2
#> 5 -0.3927281+0.8399174i Traj_6 Sim_2 TrajSim_6_2
#> 6 -0.4706470+0.8916510i Traj_6 Sim_2 TrajSim_6_2
#>
#> [[2]][[7]]
#> x y time displacementTime polar
#> 1 26.47200 15.49600 0.00 0.00 26.47200+15.49600i
#> 2 27.53162 16.19059 0.02 0.02 27.53162+16.19059i
#> 3 28.59971 16.76651 0.04 0.04 28.59971+16.76651i
#> 4 29.53895 17.34131 0.06 0.06 29.53895+17.34131i
#> 5 30.60205 18.02412 0.08 0.08 30.60205+18.02412i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_7 Sim_2 TrajSim_7_2
#> 2 1.0596248+0.6945856i Traj_7 Sim_2 TrajSim_7_2
#> 3 1.0680840+0.5759239i Traj_7 Sim_2 TrajSim_7_2
#> 4 0.9392393+0.5748027i Traj_7 Sim_2 TrajSim_7_2
#> 5 1.0631063+0.6828115i Traj_7 Sim_2 TrajSim_7_2
#>
#> [[2]][[8]]
#> x y time displacementTime polar
#> 1 13.21800 8.752000 0.00 0.00 13.21800+8.752000i
#> 2 13.62808 8.622606 0.02 0.02 13.62808+8.622606i
#> 3 14.02153 8.474348 0.04 0.04 14.02153+8.474348i
#> 4 14.38474 8.299972 0.06 0.06 14.38474+8.299972i
#> 5 14.65032 8.000951 0.08 0.08 14.65032+8.000951i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_8 Sim_2 TrajSim_8_2
#> 2 0.4100800-0.1293939i Traj_8 Sim_2 TrajSim_8_2
#> 3 0.3934525-0.1482583i Traj_8 Sim_2 TrajSim_8_2
#> 4 0.3632034-0.1743758i Traj_8 Sim_2 TrajSim_8_2
#> 5 0.2655849-0.2990211i Traj_8 Sim_2 TrajSim_8_2
#>
#> [[2]][[9]]
#> x y time displacementTime polar
#> 1 15.63800 8.164000 0.00 0.00 15.63800+8.164000i
#> 2 15.73683 7.121614 0.02 0.02 15.73683+7.121614i
#> 3 15.80270 6.107882 0.04 0.04 15.80270+6.107882i
#> 4 15.89665 5.114373 0.06 0.06 15.89665+5.114373i
#> 5 15.97757 4.121045 0.08 0.08 15.97757+4.121045i
#> displacement Trajectory Simulation TrajSim
#> 1 0.00000000+0.0000000i Traj_9 Sim_2 TrajSim_9_2
#> 2 0.09883450-1.0423857i Traj_9 Sim_2 TrajSim_9_2
#> 3 0.06586951-1.0137319i Traj_9 Sim_2 TrajSim_9_2
#> 4 0.09394280-0.9935097i Traj_9 Sim_2 TrajSim_9_2
#> 5 0.08092501-0.9933272i Traj_9 Sim_2 TrajSim_9_2
#>
#> [[2]][[10]]
#> x y time displacementTime polar
#> 1 14.698000 6.798000 0.00 0.00 14.698000+6.798000i
#> 2 13.865980 6.928262 0.02 0.02 13.865980+6.928262i
#> 3 13.080809 6.961504 0.04 0.04 13.080809+6.961504i
#> 4 12.105768 7.051254 0.06 0.06 12.105768+7.051254i
#> 5 11.201736 7.038805 0.08 0.08 11.201736+7.038805i
#> 6 10.200835 7.141120 0.10 0.10 10.200835+7.141120i
#> 7 9.306728 7.178563 0.12 0.12 9.306728+7.178563i
#> 8 8.453864 7.283949 0.14 0.14 8.453864+7.283949i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.00000000i Traj_10 Sim_2 TrajSim_10_2
#> 2 -0.8320204+0.13026167i Traj_10 Sim_2 TrajSim_10_2
#> 3 -0.7851703+0.03324238i Traj_10 Sim_2 TrajSim_10_2
#> 4 -0.9750412+0.08974984i Traj_10 Sim_2 TrajSim_10_2
#> 5 -0.9040322-0.01244873i Traj_10 Sim_2 TrajSim_10_2
#> 6 -1.0009011+0.10231519i Traj_10 Sim_2 TrajSim_10_2
#> 7 -0.8941068+0.03744293i Traj_10 Sim_2 TrajSim_10_2
#> 8 -0.8528643+0.10538542i Traj_10 Sim_2 TrajSim_10_2
#>
#> [[2]][[11]]
#> x y time displacementTime polar
#> 1 12.006000 7.316000 0.00 0.00 12.006000+7.316000i
#> 2 11.005854 7.449990 0.02 0.02 11.005854+7.449990i
#> 3 9.928442 7.573564 0.04 0.04 9.928442+7.573564i
#> 4 8.822924 7.811796 0.06 0.06 8.822924+7.811796i
#> 5 7.691043 8.069578 0.08 0.08 7.691043+8.069578i
#> displacement Trajectory Simulation TrajSim
#> 1 0.000000+0.0000000i Traj_11 Sim_2 TrajSim_11_2
#> 2 -1.000146+0.1339900i Traj_11 Sim_2 TrajSim_11_2
#> 3 -1.077411+0.1235743i Traj_11 Sim_2 TrajSim_11_2
#> 4 -1.105518+0.2382316i Traj_11 Sim_2 TrajSim_11_2
#> 5 -1.131881+0.2577819i Traj_11 Sim_2 TrajSim_11_2
#>
#>
#> [[3]]
#> [[3]][[1]]
#> x y time displacementTime polar
#> 1 36.88200 14.05600 0.00 0.00 36.88200+14.05600i
#> 2 36.28213 14.69472 0.02 0.02 36.28213+14.69472i
#> 3 35.73883 15.38386 0.04 0.04 35.73883+15.38386i
#> 4 35.22587 15.98479 0.06 0.06 35.22587+15.98479i
#> 5 34.69864 16.66349 0.08 0.08 34.69864+16.66349i
#> 6 34.20014 17.38227 0.10 0.10 34.20014+17.38227i
#> 7 33.54469 18.04469 0.12 0.12 33.54469+18.04469i
#> 8 32.83197 18.65072 0.14 0.14 32.83197+18.65072i
#> 9 32.16734 19.24329 0.16 0.16 32.16734+19.24329i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_1 Sim_3 TrajSim_1_3
#> 2 -0.5998700+0.6387241i Traj_1 Sim_3 TrajSim_1_3
#> 3 -0.5432989+0.6891309i Traj_1 Sim_3 TrajSim_1_3
#> 4 -0.5129627+0.6009358i Traj_1 Sim_3 TrajSim_1_3
#> 5 -0.5272273+0.6787000i Traj_1 Sim_3 TrajSim_1_3
#> 6 -0.4985018+0.7187765i Traj_1 Sim_3 TrajSim_1_3
#> 7 -0.6554475+0.6624262i Traj_1 Sim_3 TrajSim_1_3
#> 8 -0.7127182+0.6060234i Traj_1 Sim_3 TrajSim_1_3
#> 9 -0.6646314+0.5925754i Traj_1 Sim_3 TrajSim_1_3
#>
#> [[3]][[2]]
#> x y time displacementTime polar
#> 1 35.53200 13.51600 0.00 0.00 35.53200+13.51600i
#> 2 35.92736 14.34410 0.02 0.02 35.92736+14.34410i
#> 3 36.30953 15.23979 0.04 0.04 36.30953+15.23979i
#> 4 36.64510 16.01842 0.06 0.06 36.64510+16.01842i
#> 5 36.99435 16.92416 0.08 0.08 36.99435+16.92416i
#> 6 37.16598 17.93852 0.10 0.10 37.16598+17.93852i
#> 7 37.24693 18.97428 0.12 0.12 37.24693+18.97428i
#> 8 37.42261 20.08484 0.14 0.14 37.42261+20.08484i
#> 9 37.63176 20.95988 0.16 0.16 37.63176+20.95988i
#> displacement Trajectory Simulation TrajSim
#> 1 0.00000000+0.0000000i Traj_2 Sim_3 TrajSim_2_3
#> 2 0.39536338+0.8281017i Traj_2 Sim_3 TrajSim_2_3
#> 3 0.38216185+0.8956870i Traj_2 Sim_3 TrajSim_2_3
#> 4 0.33557805+0.7786335i Traj_2 Sim_3 TrajSim_2_3
#> 5 0.34924386+0.9057358i Traj_2 Sim_3 TrajSim_2_3
#> 6 0.17163042+1.0143596i Traj_2 Sim_3 TrajSim_2_3
#> 7 0.08095659+1.0357612i Traj_2 Sim_3 TrajSim_2_3
#> 8 0.17567118+1.1105619i Traj_2 Sim_3 TrajSim_2_3
#> 9 0.20915016+0.8750396i Traj_2 Sim_3 TrajSim_2_3
#>
#> [[3]][[3]]
#> x y time displacementTime polar
#> 1 34.54800 14.10000 0.00 0.00 34.54800+14.10000i
#> 2 34.01996 14.93598 0.02 0.02 34.01996+14.93598i
#> 3 33.35197 15.96684 0.04 0.04 33.35197+15.96684i
#> 4 32.65314 16.95796 0.06 0.06 32.65314+16.95796i
#> 5 32.05867 17.76604 0.08 0.08 32.05867+17.76604i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_3 Sim_3 TrajSim_3_3
#> 2 -0.5280375+0.8359770i Traj_3 Sim_3 TrajSim_3_3
#> 3 -0.6679878+1.0308648i Traj_3 Sim_3 TrajSim_3_3
#> 4 -0.6988394+0.9911139i Traj_3 Sim_3 TrajSim_3_3
#> 5 -0.5944659+0.8080868i Traj_3 Sim_3 TrajSim_3_3
#>
#> [[3]][[4]]
#> x y time displacementTime polar
#> 1 32.26000 14.51800 0.00 0.00 32.26000+14.51800i
#> 2 32.41681 13.54250 0.02 0.02 32.41681+13.54250i
#> 3 32.56645 12.57771 0.04 0.04 32.56645+12.57771i
#> 4 32.88826 11.55437 0.06 0.06 32.88826+11.55437i
#> 5 33.12842 10.64597 0.08 0.08 33.12842+10.64597i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_4 Sim_3 TrajSim_4_3
#> 2 0.1568066-0.9754966i Traj_4 Sim_3 TrajSim_4_3
#> 3 0.1496425-0.9647887i Traj_4 Sim_3 TrajSim_4_3
#> 4 0.3218151-1.0233452i Traj_4 Sim_3 TrajSim_4_3
#> 5 0.2401582-0.9083993i Traj_4 Sim_3 TrajSim_4_3
#>
#> [[3]][[5]]
#> x y time displacementTime polar
#> 1 28.29000 13.57800 0.00 0.00 28.29000+13.57800i
#> 2 27.49775 13.40424 0.02 0.02 27.49775+13.40424i
#> 3 26.56672 13.13060 0.04 0.04 26.56672+13.13060i
#> 4 25.71020 12.89004 0.06 0.06 25.71020+12.89004i
#> 5 24.84269 12.58525 0.08 0.08 24.84269+12.58525i
#> 6 24.17049 12.31883 0.10 0.10 24.17049+12.31883i
#> 7 23.34438 12.05388 0.12 0.12 23.34438+12.05388i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_5 Sim_3 TrajSim_5_3
#> 2 -0.7922523-0.1737632i Traj_5 Sim_3 TrajSim_5_3
#> 3 -0.9310257-0.2736416i Traj_5 Sim_3 TrajSim_5_3
#> 4 -0.8565201-0.2405588i Traj_5 Sim_3 TrajSim_5_3
#> 5 -0.8675158-0.3047853i Traj_5 Sim_3 TrajSim_5_3
#> 6 -0.6721952-0.2664192i Traj_5 Sim_3 TrajSim_5_3
#> 7 -0.8261110-0.2649508i Traj_5 Sim_3 TrajSim_5_3
#>
#> [[3]][[6]]
#> x y time displacementTime polar
#> 1 26.19800 13.69800 0.00 0.00 26.19800+13.69800i
#> 2 27.07683 13.00986 0.02 0.02 27.07683+13.00986i
#> 3 27.97124 12.34199 0.04 0.04 27.97124+12.34199i
#> 4 28.87188 11.76993 0.06 0.06 28.87188+11.76993i
#> 5 29.82383 11.22271 0.08 0.08 29.82383+11.22271i
#> 6 30.67398 10.52241 0.10 0.10 30.67398+10.52241i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_6 Sim_3 TrajSim_6_3
#> 2 0.8788311-0.6881401i Traj_6 Sim_3 TrajSim_6_3
#> 3 0.8944054-0.6678682i Traj_6 Sim_3 TrajSim_6_3
#> 4 0.9006409-0.5720597i Traj_6 Sim_3 TrajSim_6_3
#> 5 0.9519504-0.5472249i Traj_6 Sim_3 TrajSim_6_3
#> 6 0.8501489-0.7002966i Traj_6 Sim_3 TrajSim_6_3
#>
#> [[3]][[7]]
#> x y time displacementTime polar
#> 1 26.47200 15.49600 0.00 0.00 26.47200+15.49600i
#> 2 27.73900 15.93686 0.02 0.02 27.73900+15.93686i
#> 3 28.78548 16.26143 0.04 0.04 28.78548+16.26143i
#> 4 29.81754 16.64179 0.06 0.06 29.81754+16.64179i
#> 5 31.13281 17.07248 0.08 0.08 31.13281+17.07248i
#> displacement Trajectory Simulation TrajSim
#> 1 0.000000+0.0000000i Traj_7 Sim_3 TrajSim_7_3
#> 2 1.267002+0.4408610i Traj_7 Sim_3 TrajSim_7_3
#> 3 1.046477+0.3245646i Traj_7 Sim_3 TrajSim_7_3
#> 4 1.032066+0.3803626i Traj_7 Sim_3 TrajSim_7_3
#> 5 1.315268+0.4306925i Traj_7 Sim_3 TrajSim_7_3
#>
#> [[3]][[8]]
#> x y time displacementTime polar
#> 1 13.21800 8.752000 0.00 0.00 13.21800+8.752000i
#> 2 13.06363 8.377064 0.02 0.02 13.06363+8.377064i
#> 3 12.87880 7.924915 0.04 0.04 12.87880+7.924915i
#> 4 12.76183 7.602224 0.06 0.06 12.76183+7.602224i
#> 5 12.55278 7.236361 0.08 0.08 12.55278+7.236361i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_8 Sim_3 TrajSim_8_3
#> 2 -0.1543667-0.3749364i Traj_8 Sim_3 TrajSim_8_3
#> 3 -0.1848315-0.4521486i Traj_8 Sim_3 TrajSim_8_3
#> 4 -0.1169725-0.3226913i Traj_8 Sim_3 TrajSim_8_3
#> 5 -0.2090447-0.3658621i Traj_8 Sim_3 TrajSim_8_3
#>
#> [[3]][[9]]
#> x y time displacementTime polar
#> 1 15.63800 8.164000 0.00 0.00 15.63800+8.164000i
#> 2 14.55930 8.560616 0.02 0.02 14.55930+8.560616i
#> 3 13.49098 8.886133 0.04 0.04 13.49098+8.886133i
#> 4 12.51286 9.284022 0.06 0.06 12.51286+9.284022i
#> 5 11.54349 9.675492 0.08 0.08 11.54349+9.675492i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_9 Sim_3 TrajSim_9_3
#> 2 -1.0787016+0.3966160i Traj_9 Sim_3 TrajSim_9_3
#> 3 -1.0683146+0.3255170i Traj_9 Sim_3 TrajSim_9_3
#> 4 -0.9781276+0.3978895i Traj_9 Sim_3 TrajSim_9_3
#> 5 -0.9693620+0.3914691i Traj_9 Sim_3 TrajSim_9_3
#>
#> [[3]][[10]]
#> x y time displacementTime polar
#> 1 14.69800 6.798000 0.00 0.00 14.69800+6.798000i
#> 2 15.54165 6.283550 0.02 0.02 15.54165+6.283550i
#> 3 16.37422 5.833175 0.04 0.04 16.37422+5.833175i
#> 4 17.20593 5.334948 0.06 0.06 17.20593+5.334948i
#> 5 18.06321 4.877186 0.08 0.08 18.06321+4.877186i
#> 6 18.88033 4.484932 0.10 0.10 18.88033+4.484932i
#> 7 19.64295 4.047316 0.12 0.12 19.64295+4.047316i
#> 8 20.45572 3.665476 0.14 0.14 20.45572+3.665476i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_10 Sim_3 TrajSim_10_3
#> 2 0.8436521-0.5144496i Traj_10 Sim_3 TrajSim_10_3
#> 3 0.8325692-0.4503757i Traj_10 Sim_3 TrajSim_10_3
#> 4 0.8317128-0.4982272i Traj_10 Sim_3 TrajSim_10_3
#> 5 0.8572764-0.4577618i Traj_10 Sim_3 TrajSim_10_3
#> 6 0.8171157-0.3922542i Traj_10 Sim_3 TrajSim_10_3
#> 7 0.7626248-0.4376161i Traj_10 Sim_3 TrajSim_10_3
#> 8 0.8127700-0.3818391i Traj_10 Sim_3 TrajSim_10_3
#>
#> [[3]][[11]]
#> x y time displacementTime polar
#> 1 12.00600 7.316000 0.00 0.00 12.00600+7.316000i
#> 2 11.67761 6.331742 0.02 0.02 11.67761+6.331742i
#> 3 11.28995 5.314532 0.04 0.04 11.28995+5.314532i
#> 4 10.89923 4.506049 0.06 0.06 10.89923+4.506049i
#> 5 10.43849 3.609933 0.08 0.08 10.43849+3.609933i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_11 Sim_3 TrajSim_11_3
#> 2 -0.3283852-0.9842577i Traj_11 Sim_3 TrajSim_11_3
#> 3 -0.3876696-1.0172098i Traj_11 Sim_3 TrajSim_11_3
#> 4 -0.3907117-0.8084835i Traj_11 Sim_3 TrajSim_11_3
#> 5 -0.4607470-0.8961163i Traj_11 Sim_3 TrajSim_11_3
#>
#>
#> [[4]]
#> [[4]][[1]]
#> x y time displacementTime polar
#> 1 36.88200 14.05600 0.00 0.00 36.88200+14.05600i
#> 2 36.96283 14.90939 0.02 0.02 36.96283+14.90939i
#> 3 36.93537 15.78630 0.04 0.04 36.93537+15.78630i
#> 4 36.87480 16.57864 0.06 0.06 36.87480+16.57864i
#> 5 37.02249 17.50073 0.08 0.08 37.02249+17.50073i
#> 6 37.05155 18.33715 0.10 0.10 37.05155+18.33715i
#> 7 37.15773 19.19956 0.12 0.12 37.15773+19.19956i
#> 8 37.17285 20.08844 0.14 0.14 37.17285+20.08844i
#> 9 37.08474 20.98303 0.16 0.16 37.08474+20.98303i
#> displacement Trajectory Simulation TrajSim
#> 1 0.00000000+0.0000000i Traj_1 Sim_4 TrajSim_1_4
#> 2 0.08082688+0.8533869i Traj_1 Sim_4 TrajSim_1_4
#> 3 -0.02745713+0.8769164i Traj_1 Sim_4 TrajSim_1_4
#> 4 -0.06056828+0.7923317i Traj_1 Sim_4 TrajSim_1_4
#> 5 0.14768970+0.9220948i Traj_1 Sim_4 TrajSim_1_4
#> 6 0.02906373+0.8364220i Traj_1 Sim_4 TrajSim_1_4
#> 7 0.10617296+0.8624084i Traj_1 Sim_4 TrajSim_1_4
#> 8 0.01512630+0.8888783i Traj_1 Sim_4 TrajSim_1_4
#> 9 -0.08811724+0.8945961i Traj_1 Sim_4 TrajSim_1_4
#>
#> [[4]][[2]]
#> x y time displacementTime polar
#> 1 35.53200 13.516000 0.00 0.00 35.53200+13.516000i
#> 2 34.96271 12.810176 0.02 0.02 34.96271+12.810176i
#> 3 34.39153 12.095899 0.04 0.04 34.39153+12.095899i
#> 4 33.73105 11.454006 0.06 0.06 33.73105+11.454006i
#> 5 33.08414 10.773522 0.08 0.08 33.08414+10.773522i
#> 6 32.38479 10.088253 0.10 0.10 32.38479+10.088253i
#> 7 31.75961 9.467377 0.12 0.12 31.75961+ 9.467377i
#> 8 31.06614 8.796485 0.14 0.14 31.06614+ 8.796485i
#> 9 30.41287 8.271745 0.16 0.16 30.41287+ 8.271745i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_2 Sim_4 TrajSim_2_4
#> 2 -0.5692858-0.7058241i Traj_2 Sim_4 TrajSim_2_4
#> 3 -0.5711873-0.7142766i Traj_2 Sim_4 TrajSim_2_4
#> 4 -0.6604733-0.6418932i Traj_2 Sim_4 TrajSim_2_4
#> 5 -0.6469136-0.6804841i Traj_2 Sim_4 TrajSim_2_4
#> 6 -0.6993459-0.6852689i Traj_2 Sim_4 TrajSim_2_4
#> 7 -0.6251856-0.6208763i Traj_2 Sim_4 TrajSim_2_4
#> 8 -0.6934687-0.6708918i Traj_2 Sim_4 TrajSim_2_4
#> 9 -0.6532690-0.5247405i Traj_2 Sim_4 TrajSim_2_4
#>
#> [[4]][[3]]
#> x y time displacementTime polar
#> 1 34.54800 14.10000 0.00 0.00 34.54800+14.10000i
#> 2 35.26581 15.00588 0.02 0.02 35.26581+15.00588i
#> 3 35.98205 15.81034 0.04 0.04 35.98205+15.81034i
#> 4 36.69734 16.57506 0.06 0.06 36.69734+16.57506i
#> 5 37.45702 17.33837 0.08 0.08 37.45702+17.33837i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_3 Sim_4 TrajSim_3_4
#> 2 0.7178057+0.9058757i Traj_3 Sim_4 TrajSim_3_4
#> 3 0.7162488+0.8044619i Traj_3 Sim_4 TrajSim_3_4
#> 4 0.7152849+0.7647190i Traj_3 Sim_4 TrajSim_3_4
#> 5 0.7596781+0.7633183i Traj_3 Sim_4 TrajSim_3_4
#>
#> [[4]][[4]]
#> x y time displacementTime polar
#> 1 32.26000 14.51800 0.00 0.00 32.26000+14.51800i
#> 2 32.05955 13.59138 0.02 0.02 32.05955+13.59138i
#> 3 31.74730 12.54174 0.04 0.04 31.74730+12.54174i
#> 4 31.36153 11.51381 0.06 0.06 31.36153+11.51381i
#> 5 30.96468 10.56916 0.08 0.08 30.96468+10.56916i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_4 Sim_4 TrajSim_4_4
#> 2 -0.2004516-0.9266162i Traj_4 Sim_4 TrajSim_4_4
#> 3 -0.3122504-1.0496397i Traj_4 Sim_4 TrajSim_4_4
#> 4 -0.3857637-1.0279386i Traj_4 Sim_4 TrajSim_4_4
#> 5 -0.3968503-0.9446504i Traj_4 Sim_4 TrajSim_4_4
#>
#> [[4]][[5]]
#> x y time displacementTime polar
#> 1 28.29000 13.57800 0.00 0.00 28.29000+13.57800i
#> 2 28.98055 13.11387 0.02 0.02 28.98055+13.11387i
#> 3 29.68361 12.59861 0.04 0.04 29.68361+12.59861i
#> 4 30.39419 12.16049 0.06 0.06 30.39419+12.16049i
#> 5 31.07779 11.73061 0.08 0.08 31.07779+11.73061i
#> 6 31.88925 11.32366 0.10 0.10 31.88925+11.32366i
#> 7 32.85967 10.92828 0.12 0.12 32.85967+10.92828i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_5 Sim_4 TrajSim_5_4
#> 2 0.6905548-0.4641337i Traj_5 Sim_4 TrajSim_5_4
#> 3 0.7030518-0.5152528i Traj_5 Sim_4 TrajSim_5_4
#> 4 0.7105834-0.4381191i Traj_5 Sim_4 TrajSim_5_4
#> 5 0.6836001-0.4298836i Traj_5 Sim_4 TrajSim_5_4
#> 6 0.8114586-0.4069462i Traj_5 Sim_4 TrajSim_5_4
#> 7 0.9704165-0.3953858i Traj_5 Sim_4 TrajSim_5_4
#>
#> [[4]][[6]]
#> x y time displacementTime polar
#> 1 26.19800 13.698000 0.00 0.00 26.19800+13.698000i
#> 2 25.38451 12.870966 0.02 0.02 25.38451+12.870966i
#> 3 24.58868 12.026624 0.04 0.04 24.58868+12.026624i
#> 4 23.80956 11.218553 0.06 0.06 23.80956+11.218553i
#> 5 23.12388 10.445932 0.08 0.08 23.12388+10.445932i
#> 6 22.33195 9.719423 0.10 0.10 22.33195+ 9.719423i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_6 Sim_4 TrajSim_6_4
#> 2 -0.8134909-0.8270336i Traj_6 Sim_4 TrajSim_6_4
#> 3 -0.7958276-0.8443421i Traj_6 Sim_4 TrajSim_6_4
#> 4 -0.7791237-0.8080717i Traj_6 Sim_4 TrajSim_6_4
#> 5 -0.6856742-0.7726201i Traj_6 Sim_4 TrajSim_6_4
#> 6 -0.7919366-0.7265099i Traj_6 Sim_4 TrajSim_6_4
#>
#> [[4]][[7]]
#> x y time displacementTime polar
#> 1 26.47200 15.49600 0.00 0.00 26.47200+15.49600i
#> 2 26.19650 16.85475 0.02 0.02 26.19650+16.85475i
#> 3 25.88871 18.06380 0.04 0.04 25.88871+18.06380i
#> 4 25.60988 19.13734 0.06 0.06 25.60988+19.13734i
#> 5 25.26386 20.26410 0.08 0.08 25.26386+20.26410i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.000000i Traj_7 Sim_4 TrajSim_7_4
#> 2 -0.2754961+1.358754i Traj_7 Sim_4 TrajSim_7_4
#> 3 -0.3077933+1.209049i Traj_7 Sim_4 TrajSim_7_4
#> 4 -0.2788321+1.073539i Traj_7 Sim_4 TrajSim_7_4
#> 5 -0.3460215+1.126754i Traj_7 Sim_4 TrajSim_7_4
#>
#> [[4]][[8]]
#> x y time displacementTime polar
#> 1 13.21800 8.752000 0.00 0.00 13.21800+8.752000i
#> 2 13.61993 8.973747 0.02 0.02 13.61993+8.973747i
#> 3 13.98886 9.174364 0.04 0.04 13.98886+9.174364i
#> 4 14.37218 9.343610 0.06 0.06 14.37218+9.343610i
#> 5 14.78985 9.424342 0.08 0.08 14.78985+9.424342i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.00000000i Traj_8 Sim_4 TrajSim_8_4
#> 2 0.4019256+0.22174676i Traj_8 Sim_4 TrajSim_8_4
#> 3 0.3689302+0.20061710i Traj_8 Sim_4 TrajSim_8_4
#> 4 0.3833254+0.16924617i Traj_8 Sim_4 TrajSim_8_4
#> 5 0.4176668+0.08073173i Traj_8 Sim_4 TrajSim_8_4
#>
#> [[4]][[9]]
#> x y time displacementTime polar
#> 1 15.63800 8.164000 0.00 0.00 15.63800+8.164000i
#> 2 15.35053 7.074461 0.02 0.02 15.35053+7.074461i
#> 3 15.12468 6.164895 0.04 0.04 15.12468+6.164895i
#> 4 14.78838 5.066098 0.06 0.06 14.78838+5.066098i
#> 5 14.51581 4.086988 0.08 0.08 14.51581+4.086988i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_9 Sim_4 TrajSim_9_4
#> 2 -0.2874715-1.0895389i Traj_9 Sim_4 TrajSim_9_4
#> 3 -0.2258523-0.9095666i Traj_9 Sim_4 TrajSim_9_4
#> 4 -0.3362969-1.0987969i Traj_9 Sim_4 TrajSim_9_4
#> 5 -0.2725709-0.9791095i Traj_9 Sim_4 TrajSim_9_4
#>
#> [[4]][[10]]
#> x y time displacementTime polar
#> 1 14.69800 6.798000 0.00 0.00 14.69800+6.798000i
#> 2 13.99319 6.326258 0.02 0.02 13.99319+6.326258i
#> 3 13.21832 5.755906 0.04 0.04 13.21832+5.755906i
#> 4 12.54323 5.076948 0.06 0.06 12.54323+5.076948i
#> 5 11.94202 4.355712 0.08 0.08 11.94202+4.355712i
#> 6 11.36560 3.585184 0.10 0.10 11.36560+3.585184i
#> 7 10.81781 2.775200 0.12 0.12 10.81781+2.775200i
#> 8 10.13714 2.050392 0.14 0.14 10.13714+2.050392i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_10 Sim_4 TrajSim_10_4
#> 2 -0.7048139-0.4717417i Traj_10 Sim_4 TrajSim_10_4
#> 3 -0.7748614-0.5703525i Traj_10 Sim_4 TrajSim_10_4
#> 4 -0.6750957-0.6789578i Traj_10 Sim_4 TrajSim_10_4
#> 5 -0.6012127-0.7212356i Traj_10 Sim_4 TrajSim_10_4
#> 6 -0.5764202-0.7705280i Traj_10 Sim_4 TrajSim_10_4
#> 7 -0.5477879-0.8099843i Traj_10 Sim_4 TrajSim_10_4
#> 8 -0.6806718-0.7248085i Traj_10 Sim_4 TrajSim_10_4
#>
#> [[4]][[11]]
#> x y time displacementTime polar
#> 1 12.006000 7.316000 0.00 0.00 12.006000+7.316000i
#> 2 10.824005 7.448256 0.02 0.02 10.824005+7.448256i
#> 3 9.889462 7.489619 0.04 0.04 9.889462+7.489619i
#> 4 8.720608 7.397635 0.06 0.06 8.720608+7.397635i
#> 5 7.578777 7.418435 0.08 0.08 7.578777+7.418435i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.00000000i Traj_11 Sim_4 TrajSim_11_4
#> 2 -1.1819951+0.13225597i Traj_11 Sim_4 TrajSim_11_4
#> 3 -0.9345434+0.04136337i Traj_11 Sim_4 TrajSim_11_4
#> 4 -1.1688535-0.09198394i Traj_11 Sim_4 TrajSim_11_4
#> 5 -1.1418312+0.02080004i Traj_11 Sim_4 TrajSim_11_4
#>
#>
#> [[5]]
#> [[5]][[1]]
#> x y time displacementTime polar
#> 1 36.88200 14.05600 0.00 0.00 36.88200+14.05600i
#> 2 36.81110 14.95341 0.02 0.02 36.81110+14.95341i
#> 3 36.63578 15.80397 0.04 0.04 36.63578+15.80397i
#> 4 36.35640 16.65548 0.06 0.06 36.35640+16.65548i
#> 5 36.01667 17.55995 0.08 0.08 36.01667+17.55995i
#> 6 35.85867 18.41088 0.10 0.10 35.85867+18.41088i
#> 7 35.37430 19.17873 0.12 0.12 35.37430+19.17873i
#> 8 34.79487 19.87468 0.14 0.14 34.79487+19.87468i
#> 9 34.13932 20.56500 0.16 0.16 34.13932+20.56500i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_1 Sim_5 TrajSim_1_5
#> 2 -0.0708969+0.8974142i Traj_1 Sim_5 TrajSim_1_5
#> 3 -0.1753197+0.8505540i Traj_1 Sim_5 TrajSim_1_5
#> 4 -0.2793852+0.8515112i Traj_1 Sim_5 TrajSim_1_5
#> 5 -0.3397290+0.9044735i Traj_1 Sim_5 TrajSim_1_5
#> 6 -0.1579992+0.8509227i Traj_1 Sim_5 TrajSim_1_5
#> 7 -0.4843719+0.7678561i Traj_1 Sim_5 TrajSim_1_5
#> 8 -0.5794314+0.6959461i Traj_1 Sim_5 TrajSim_1_5
#> 9 -0.6555432+0.6903209i Traj_1 Sim_5 TrajSim_1_5
#>
#> [[5]][[2]]
#> x y time displacementTime polar
#> 1 35.53200 13.51600 0.00 0.00 35.53200+13.51600i
#> 2 35.84845 14.30283 0.02 0.02 35.84845+14.30283i
#> 3 36.20470 15.09513 0.04 0.04 36.20470+15.09513i
#> 4 36.50366 15.92626 0.06 0.06 36.50366+15.92626i
#> 5 36.75355 16.77423 0.08 0.08 36.75355+16.77423i
#> 6 37.03086 17.73492 0.10 0.10 37.03086+17.73492i
#> 7 37.49395 18.50130 0.12 0.12 37.49395+18.50130i
#> 8 37.93335 19.42493 0.14 0.14 37.93335+19.42493i
#> 9 38.20259 20.25416 0.16 0.16 38.20259+20.25416i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_2 Sim_5 TrajSim_2_5
#> 2 0.3164522+0.7868280i Traj_2 Sim_5 TrajSim_2_5
#> 3 0.3562473+0.7923052i Traj_2 Sim_5 TrajSim_2_5
#> 4 0.2989554+0.8311315i Traj_2 Sim_5 TrajSim_2_5
#> 5 0.2498921+0.8479642i Traj_2 Sim_5 TrajSim_2_5
#> 6 0.2773087+0.9606948i Traj_2 Sim_5 TrajSim_2_5
#> 7 0.4630922+0.7663779i Traj_2 Sim_5 TrajSim_2_5
#> 8 0.4394047+0.9236313i Traj_2 Sim_5 TrajSim_2_5
#> 9 0.2692367+0.8292315i Traj_2 Sim_5 TrajSim_2_5
#>
#> [[5]][[3]]
#> x y time displacementTime polar
#> 1 34.54800 14.10000 0.00 0.00 34.54800+14.10000i
#> 2 35.10896 13.10656 0.02 0.02 35.10896+13.10656i
#> 3 35.66963 12.08196 0.04 0.04 35.66963+12.08196i
#> 4 36.22013 11.09593 0.06 0.06 36.22013+11.09593i
#> 5 36.74797 10.21328 0.08 0.08 36.74797+10.21328i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_3 Sim_5 TrajSim_3_5
#> 2 0.5609625-0.9934422i Traj_3 Sim_5 TrajSim_3_5
#> 3 0.5606626-1.0246016i Traj_3 Sim_5 TrajSim_3_5
#> 4 0.5505083-0.9860222i Traj_3 Sim_5 TrajSim_3_5
#> 5 0.5278336-0.8826580i Traj_3 Sim_5 TrajSim_3_5
#>
#> [[5]][[4]]
#> x y time displacementTime polar
#> 1 32.26000 14.51800 0.00 0.00 32.26000+14.51800i
#> 2 31.84471 15.40874 0.02 0.02 31.84471+15.40874i
#> 3 31.33973 16.40682 0.04 0.04 31.33973+16.40682i
#> 4 30.88276 17.35512 0.06 0.06 30.88276+17.35512i
#> 5 30.58074 18.37172 0.08 0.08 30.58074+18.37172i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_4 Sim_5 TrajSim_4_5
#> 2 -0.4152890+0.8907355i Traj_4 Sim_5 TrajSim_4_5
#> 3 -0.5049823+0.9980800i Traj_4 Sim_5 TrajSim_4_5
#> 4 -0.4569688+0.9483083i Traj_4 Sim_5 TrajSim_4_5
#> 5 -0.3020192+1.0165994i Traj_4 Sim_5 TrajSim_4_5
#>
#> [[5]][[5]]
#> x y time displacementTime polar
#> 1 28.29000 13.578000 0.00 0.00 28.29000+13.578000i
#> 2 27.97023 12.822236 0.02 0.02 27.97023+12.822236i
#> 3 27.59969 12.094963 0.04 0.04 27.59969+12.094963i
#> 4 27.15854 11.351135 0.06 0.06 27.15854+11.351135i
#> 5 26.59378 10.597226 0.08 0.08 26.59378+10.597226i
#> 6 26.39568 9.940516 0.10 0.10 26.39568+ 9.940516i
#> 7 26.24816 9.233231 0.12 0.12 26.24816+ 9.233231i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_5 Sim_5 TrajSim_5_5
#> 2 -0.3197673-0.7557636i Traj_5 Sim_5 TrajSim_5_5
#> 3 -0.3705431-0.7272736i Traj_5 Sim_5 TrajSim_5_5
#> 4 -0.4411479-0.7438279i Traj_5 Sim_5 TrajSim_5_5
#> 5 -0.5647622-0.7539092i Traj_5 Sim_5 TrajSim_5_5
#> 6 -0.1981019-0.6567096i Traj_5 Sim_5 TrajSim_5_5
#> 7 -0.1475182-0.7072849i Traj_5 Sim_5 TrajSim_5_5
#>
#> [[5]][[6]]
#> x y time displacementTime polar
#> 1 26.19800 13.69800 0.00 0.00 26.19800+13.69800i
#> 2 26.87889 14.25137 0.02 0.02 26.87889+14.25137i
#> 3 27.66628 14.97844 0.04 0.04 27.66628+14.97844i
#> 4 28.45502 15.61962 0.06 0.06 28.45502+15.61962i
#> 5 29.29736 16.21230 0.08 0.08 29.29736+16.21230i
#> 6 30.17425 16.89077 0.10 0.10 30.17425+16.89077i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_6 Sim_5 TrajSim_6_5
#> 2 0.6808876+0.5533675i Traj_6 Sim_5 TrajSim_6_5
#> 3 0.7873920+0.7270769i Traj_6 Sim_5 TrajSim_6_5
#> 4 0.7887423+0.6411762i Traj_6 Sim_5 TrajSim_6_5
#> 5 0.8423380+0.5926792i Traj_6 Sim_5 TrajSim_6_5
#> 6 0.8768885+0.6784681i Traj_6 Sim_5 TrajSim_6_5
#>
#> [[5]][[7]]
#> x y time displacementTime polar
#> 1 26.47200 15.49600 0.00 0.00 26.47200+15.49600i
#> 2 27.75637 15.39104 0.02 0.02 27.75637+15.39104i
#> 3 29.05083 15.31233 0.04 0.04 29.05083+15.31233i
#> 4 30.26206 15.23530 0.06 0.06 30.26206+15.23530i
#> 5 31.60363 15.11037 0.08 0.08 31.60363+15.11037i
#> displacement Trajectory Simulation TrajSim
#> 1 0.000000+0.00000000i Traj_7 Sim_5 TrajSim_7_5
#> 2 1.284372-0.10495717i Traj_7 Sim_5 TrajSim_7_5
#> 3 1.294458-0.07871662i Traj_7 Sim_5 TrajSim_7_5
#> 4 1.211229-0.07702168i Traj_7 Sim_5 TrajSim_7_5
#> 5 1.341575-0.12493371i Traj_7 Sim_5 TrajSim_7_5
#>
#> [[5]][[8]]
#> x y time displacementTime polar
#> 1 13.21800 8.752000 0.00 0.00 13.21800+8.752000i
#> 2 12.95050 9.084546 0.02 0.02 12.95050+9.084546i
#> 3 12.61826 9.363118 0.04 0.04 12.61826+9.363118i
#> 4 12.29086 9.619165 0.06 0.06 12.29086+9.619165i
#> 5 12.04049 9.983272 0.08 0.08 12.04049+9.983272i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_8 Sim_5 TrajSim_8_5
#> 2 -0.2674986+0.3325461i Traj_8 Sim_5 TrajSim_8_5
#> 3 -0.3322376+0.2785717i Traj_8 Sim_5 TrajSim_8_5
#> 4 -0.3274012+0.2560472i Traj_8 Sim_5 TrajSim_8_5
#> 5 -0.2503740+0.3641065i Traj_8 Sim_5 TrajSim_8_5
#>
#> [[5]][[9]]
#> x y time displacementTime polar
#> 1 15.63800 8.164000 0.00 0.00 15.63800+ 8.164000i
#> 2 16.43714 8.657572 0.02 0.02 16.43714+ 8.657572i
#> 3 17.36392 9.182890 0.04 0.04 17.36392+ 9.182890i
#> 4 18.33196 9.674545 0.06 0.06 18.33196+ 9.674545i
#> 5 19.31875 10.072323 0.08 0.08 19.31875+10.072323i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_9 Sim_5 TrajSim_9_5
#> 2 0.7991422+0.4935725i Traj_9 Sim_5 TrajSim_9_5
#> 3 0.9267761+0.5253174i Traj_9 Sim_5 TrajSim_9_5
#> 4 0.9680435+0.4916550i Traj_9 Sim_5 TrajSim_9_5
#> 5 0.9867853+0.3977782i Traj_9 Sim_5 TrajSim_9_5
#>
#> [[5]][[10]]
#> x y time displacementTime polar
#> 1 14.69800 6.798000 0.00 0.00 14.69800+6.798000i
#> 2 15.17841 5.930890 0.02 0.02 15.17841+5.930890i
#> 3 15.63141 5.002154 0.04 0.04 15.63141+5.002154i
#> 4 16.02023 4.140637 0.06 0.06 16.02023+4.140637i
#> 5 16.28066 3.356539 0.08 0.08 16.28066+3.356539i
#> 6 16.64474 2.633683 0.10 0.10 16.64474+2.633683i
#> 7 17.10742 1.847613 0.12 0.12 17.10742+1.847613i
#> 8 17.56566 1.001902 0.14 0.14 17.56566+1.001902i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_10 Sim_5 TrajSim_10_5
#> 2 0.4804082-0.8671099i Traj_10 Sim_5 TrajSim_10_5
#> 3 0.4530026-0.9287359i Traj_10 Sim_5 TrajSim_10_5
#> 4 0.3888151-0.8615170i Traj_10 Sim_5 TrajSim_10_5
#> 5 0.2604384-0.7840983i Traj_10 Sim_5 TrajSim_10_5
#> 6 0.3640763-0.7228557i Traj_10 Sim_5 TrajSim_10_5
#> 7 0.4626826-0.7860708i Traj_10 Sim_5 TrajSim_10_5
#> 8 0.4582415-0.8457105i Traj_10 Sim_5 TrajSim_10_5
#>
#> [[5]][[11]]
#> x y time displacementTime polar
#> 1 12.00600 7.316000 0.00 0.00 12.00600+7.316000i
#> 2 13.21544 7.317748 0.02 0.02 13.21544+7.317748i
#> 3 14.38431 7.324175 0.04 0.04 14.38431+7.324175i
#> 4 15.51581 7.283274 0.06 0.06 15.51581+7.283274i
#> 5 16.49627 7.297625 0.08 0.08 16.49627+7.297625i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.000000000i Traj_11 Sim_5 TrajSim_11_5
#> 2 1.2094417+0.001748148i Traj_11 Sim_5 TrajSim_11_5
#> 3 1.1688674+0.006426687i Traj_11 Sim_5 TrajSim_11_5
#> 4 1.1314968-0.040900661i Traj_11 Sim_5 TrajSim_11_5
#> 5 0.9804657+0.014350809i Traj_11 Sim_5 TrajSim_11_5
#>
#>
#> [[6]]
#> [[6]][[1]]
#> x y time displacementTime polar
#> 1 36.88200 14.05600 0.00 0.00 36.88200+14.05600i
#> 2 37.77994 14.27214 0.02 0.02 37.77994+14.27214i
#> 3 38.63759 14.50080 0.04 0.04 38.63759+14.50080i
#> 4 39.43817 14.68341 0.06 0.06 39.43817+14.68341i
#> 5 40.18910 14.96919 0.08 0.08 40.18910+14.96919i
#> 6 40.96423 15.05212 0.10 0.10 40.96423+15.05212i
#> 7 41.85166 15.19959 0.12 0.12 41.85166+15.19959i
#> 8 42.73480 15.33374 0.14 0.14 42.73480+15.33374i
#> 9 43.58787 15.55278 0.16 0.16 43.58787+15.55278i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_1 Sim_6 TrajSim_1_6
#> 2 0.8979405+0.2161405i Traj_1 Sim_6 TrajSim_1_6
#> 3 0.8576448+0.2286573i Traj_1 Sim_6 TrajSim_1_6
#> 4 0.8005889+0.1826093i Traj_1 Sim_6 TrajSim_1_6
#> 5 0.7509253+0.2857809i Traj_1 Sim_6 TrajSim_1_6
#> 6 0.7751341+0.0829332i Traj_1 Sim_6 TrajSim_1_6
#> 7 0.8874252+0.1474690i Traj_1 Sim_6 TrajSim_1_6
#> 8 0.8831402+0.1341497i Traj_1 Sim_6 TrajSim_1_6
#> 9 0.8530703+0.2190448i Traj_1 Sim_6 TrajSim_1_6
#>
#> [[6]][[2]]
#> x y time displacementTime polar
#> 1 35.53200 13.516000 0.00 0.00 35.53200+13.516000i
#> 2 35.23871 12.666845 0.02 0.02 35.23871+12.666845i
#> 3 34.80485 11.698608 0.04 0.04 34.80485+11.698608i
#> 4 34.53420 10.891056 0.06 0.06 34.53420+10.891056i
#> 5 34.13804 10.125500 0.08 0.08 34.13804+10.125500i
#> 6 33.75185 9.341740 0.10 0.10 33.75185+ 9.341740i
#> 7 33.30458 8.399033 0.12 0.12 33.30458+ 8.399033i
#> 8 32.99156 7.344792 0.14 0.14 32.99156+ 7.344792i
#> 9 32.78156 6.586421 0.16 0.16 32.78156+ 6.586421i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_2 Sim_6 TrajSim_2_6
#> 2 -0.2932894-0.8491554i Traj_2 Sim_6 TrajSim_2_6
#> 3 -0.4338585-0.9682361i Traj_2 Sim_6 TrajSim_2_6
#> 4 -0.2706508-0.8075522i Traj_2 Sim_6 TrajSim_2_6
#> 5 -0.3961572-0.7655558i Traj_2 Sim_6 TrajSim_2_6
#> 6 -0.3861972-0.7837609i Traj_2 Sim_6 TrajSim_2_6
#> 7 -0.4472641-0.9427062i Traj_2 Sim_6 TrajSim_2_6
#> 8 -0.3130275-1.0542411i Traj_2 Sim_6 TrajSim_2_6
#> 9 -0.2099953-0.7583711i Traj_2 Sim_6 TrajSim_2_6
#>
#> [[6]][[3]]
#> x y time displacementTime polar
#> 1 34.54800 14.10000 0.00 0.00 34.54800+14.10000i
#> 2 34.72661 15.34318 0.02 0.02 34.72661+15.34318i
#> 3 34.88888 16.30222 0.04 0.04 34.88888+16.30222i
#> 4 34.99436 17.33583 0.06 0.06 34.99436+17.33583i
#> 5 35.09334 18.39689 0.08 0.08 35.09334+18.39689i
#> displacement Trajectory Simulation TrajSim
#> 1 0.00000000+0.0000000i Traj_3 Sim_6 TrajSim_3_6
#> 2 0.17860590+1.2431763i Traj_3 Sim_6 TrajSim_3_6
#> 3 0.16227857+0.9590477i Traj_3 Sim_6 TrajSim_3_6
#> 4 0.10547741+1.0336039i Traj_3 Sim_6 TrajSim_3_6
#> 5 0.09897854+1.0610620i Traj_3 Sim_6 TrajSim_3_6
#>
#> [[6]][[4]]
#> x y time displacementTime polar
#> 1 32.26000 14.51800 0.00 0.00 32.26000+14.51800i
#> 2 31.45564 14.32861 0.02 0.02 31.45564+14.32861i
#> 3 30.37923 14.15424 0.04 0.04 30.37923+14.15424i
#> 4 29.41674 13.83742 0.06 0.06 29.41674+13.83742i
#> 5 28.43167 13.56055 0.08 0.08 28.43167+13.56055i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_4 Sim_6 TrajSim_4_6
#> 2 -0.8043623-0.1893893i Traj_4 Sim_6 TrajSim_4_6
#> 3 -1.0764075-0.1743715i Traj_4 Sim_6 TrajSim_4_6
#> 4 -0.9624901-0.3168204i Traj_4 Sim_6 TrajSim_4_6
#> 5 -0.9850725-0.2768737i Traj_4 Sim_6 TrajSim_4_6
#>
#> [[6]][[5]]
#> x y time displacementTime polar
#> 1 28.29000 13.578000 0.00 0.00 28.29000+13.578000i
#> 2 27.62680 13.068587 0.02 0.02 27.62680+13.068587i
#> 3 27.12125 12.577403 0.04 0.04 27.12125+12.577403i
#> 4 26.60252 12.083807 0.06 0.06 26.60252+12.083807i
#> 5 26.09878 11.321921 0.08 0.08 26.09878+11.321921i
#> 6 25.72223 10.527584 0.10 0.10 25.72223+10.527584i
#> 7 25.40853 9.565199 0.12 0.12 25.40853+ 9.565199i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_5 Sim_6 TrajSim_5_6
#> 2 -0.6631993-0.5094131i Traj_5 Sim_6 TrajSim_5_6
#> 3 -0.5055530-0.4911837i Traj_5 Sim_6 TrajSim_5_6
#> 4 -0.5187263-0.4935961i Traj_5 Sim_6 TrajSim_5_6
#> 5 -0.5037450-0.7618858i Traj_5 Sim_6 TrajSim_5_6
#> 6 -0.3765486-0.7943377i Traj_5 Sim_6 TrajSim_5_6
#> 7 -0.3136940-0.9623846i Traj_5 Sim_6 TrajSim_5_6
#>
#> [[6]][[6]]
#> x y time displacementTime polar
#> 1 26.19800 13.69800 0.00 0.00 26.19800+13.69800i
#> 2 26.89857 14.34063 0.02 0.02 26.89857+14.34063i
#> 3 27.69098 15.01962 0.04 0.04 27.69098+15.01962i
#> 4 28.55103 15.86735 0.06 0.06 28.55103+15.86735i
#> 5 29.17385 16.70458 0.08 0.08 29.17385+16.70458i
#> 6 29.76030 17.64817 0.10 0.10 29.76030+17.64817i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_6 Sim_6 TrajSim_6_6
#> 2 0.7005746+0.6426280i Traj_6 Sim_6 TrajSim_6_6
#> 3 0.7924022+0.6789897i Traj_6 Sim_6 TrajSim_6_6
#> 4 0.8600496+0.8477336i Traj_6 Sim_6 TrajSim_6_6
#> 5 0.6228211+0.8372333i Traj_6 Sim_6 TrajSim_6_6
#> 6 0.5864525+0.9435814i Traj_6 Sim_6 TrajSim_6_6
#>
#> [[6]][[7]]
#> x y time displacementTime polar
#> 1 26.47200 15.49600 0.00 0.00 26.47200+15.49600i
#> 2 25.36902 15.70703 0.02 0.02 25.36902+15.70703i
#> 3 24.16884 15.96496 0.04 0.04 24.16884+15.96496i
#> 4 22.68790 16.36899 0.06 0.06 22.68790+16.36899i
#> 5 21.48362 16.76624 0.08 0.08 21.48362+16.76624i
#> displacement Trajectory Simulation TrajSim
#> 1 0.000000+0.0000000i Traj_7 Sim_6 TrajSim_7_6
#> 2 -1.102984+0.2110348i Traj_7 Sim_6 TrajSim_7_6
#> 3 -1.200179+0.2579295i Traj_7 Sim_6 TrajSim_7_6
#> 4 -1.480939+0.4040214i Traj_7 Sim_6 TrajSim_7_6
#> 5 -1.204279+0.3972580i Traj_7 Sim_6 TrajSim_7_6
#>
#> [[6]][[8]]
#> x y time displacementTime polar
#> 1 13.21800 8.752000 0.00 0.00 13.21800+8.752000i
#> 2 13.23946 8.331289 0.02 0.02 13.23946+8.331289i
#> 3 13.33174 7.972184 0.04 0.04 13.33174+7.972184i
#> 4 13.47161 7.612664 0.06 0.06 13.47161+7.612664i
#> 5 13.75571 7.290837 0.08 0.08 13.75571+7.290837i
#> displacement Trajectory Simulation TrajSim
#> 1 0.00000000+0.0000000i Traj_8 Sim_6 TrajSim_8_6
#> 2 0.02146194-0.4207115i Traj_8 Sim_6 TrajSim_8_6
#> 3 0.09227958-0.3591049i Traj_8 Sim_6 TrajSim_8_6
#> 4 0.13986899-0.3595194i Traj_8 Sim_6 TrajSim_8_6
#> 5 0.28409952-0.3218277i Traj_8 Sim_6 TrajSim_8_6
#>
#> [[6]][[9]]
#> x y time displacementTime polar
#> 1 15.63800 8.164000 0.00 0.00 15.63800+ 8.164000i
#> 2 15.29252 9.210013 0.02 0.02 15.29252+ 9.210013i
#> 3 15.13938 10.251785 0.04 0.04 15.13938+10.251785i
#> 4 14.78501 11.296631 0.06 0.06 14.78501+11.296631i
#> 5 14.49123 12.341907 0.08 0.08 14.49123+12.341907i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.000000i Traj_9 Sim_6 TrajSim_9_6
#> 2 -0.3454757+1.046013i Traj_9 Sim_6 TrajSim_9_6
#> 3 -0.1531399+1.041772i Traj_9 Sim_6 TrajSim_9_6
#> 4 -0.3543697+1.044847i Traj_9 Sim_6 TrajSim_9_6
#> 5 -0.2937832+1.045276i Traj_9 Sim_6 TrajSim_9_6
#>
#> [[6]][[10]]
#> x y time displacementTime polar
#> 1 14.69800 6.798000 0.00 0.00 14.69800+ 6.798000i
#> 2 14.35571 7.726193 0.02 0.02 14.35571+ 7.726193i
#> 3 14.00224 8.511239 0.04 0.04 14.00224+ 8.511239i
#> 4 13.55481 9.446349 0.06 0.06 13.55481+ 9.446349i
#> 5 13.25976 10.331591 0.08 0.08 13.25976+10.331591i
#> 6 12.99227 11.142984 0.10 0.10 12.99227+11.142984i
#> 7 12.64263 12.060264 0.12 0.12 12.64263+12.060264i
#> 8 12.33941 12.889608 0.14 0.14 12.33941+12.889608i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_10 Sim_6 TrajSim_10_6
#> 2 -0.3422935+0.9281928i Traj_10 Sim_6 TrajSim_10_6
#> 3 -0.3534624+0.7850461i Traj_10 Sim_6 TrajSim_10_6
#> 4 -0.4474292+0.9351098i Traj_10 Sim_6 TrajSim_10_6
#> 5 -0.2950581+0.8852419i Traj_10 Sim_6 TrajSim_10_6
#> 6 -0.2674835+0.8113931i Traj_10 Sim_6 TrajSim_10_6
#> 7 -0.3496454+0.9172802i Traj_10 Sim_6 TrajSim_10_6
#> 8 -0.3032216+0.8293440i Traj_10 Sim_6 TrajSim_10_6
#>
#> [[6]][[11]]
#> x y time displacementTime polar
#> 1 12.00600 7.316000 0.00 0.00 12.00600+7.316000i
#> 2 13.00821 7.874364 0.02 0.02 13.00821+7.874364i
#> 3 13.90484 8.275351 0.04 0.04 13.90484+8.275351i
#> 4 15.01225 8.834911 0.06 0.06 15.01225+8.834911i
#> 5 15.92543 9.401172 0.08 0.08 15.92543+9.401172i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_11 Sim_6 TrajSim_11_6
#> 2 1.0022077+0.5583636i Traj_11 Sim_6 TrajSim_11_6
#> 3 0.8966309+0.4009876i Traj_11 Sim_6 TrajSim_11_6
#> 4 1.1074123+0.5595597i Traj_11 Sim_6 TrajSim_11_6
#> 5 0.9131770+0.5662615i Traj_11 Sim_6 TrajSim_11_6
#>
#>
#> [[7]]
#> [[7]][[1]]
#> x y time displacementTime polar
#> 1 36.88200 14.05600 0.00 0.00 36.88200+14.05600i
#> 2 37.69507 14.42259 0.02 0.02 37.69507+14.42259i
#> 3 38.43131 14.78922 0.04 0.04 38.43131+14.78922i
#> 4 39.21359 15.02703 0.06 0.06 39.21359+15.02703i
#> 5 39.91404 15.39978 0.08 0.08 39.91404+15.39978i
#> 6 40.73523 15.70242 0.10 0.10 40.73523+15.70242i
#> 7 41.63665 16.03259 0.12 0.12 41.63665+16.03259i
#> 8 42.52477 16.24711 0.14 0.14 42.52477+16.24711i
#> 9 43.41214 16.57371 0.16 0.16 43.41214+16.57371i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_1 Sim_7 TrajSim_1_7
#> 2 0.8130749+0.3665879i Traj_1 Sim_7 TrajSim_1_7
#> 3 0.7362394+0.3666338i Traj_1 Sim_7 TrajSim_1_7
#> 4 0.7822793+0.2378053i Traj_1 Sim_7 TrajSim_1_7
#> 5 0.7004460+0.3727530i Traj_1 Sim_7 TrajSim_1_7
#> 6 0.8211883+0.3026391i Traj_1 Sim_7 TrajSim_1_7
#> 7 0.9014189+0.3301665i Traj_1 Sim_7 TrajSim_1_7
#> 8 0.8881275+0.2145208i Traj_1 Sim_7 TrajSim_1_7
#> 9 0.8873618+0.3266046i Traj_1 Sim_7 TrajSim_1_7
#>
#> [[7]][[2]]
#> x y time displacementTime polar
#> 1 35.53200 13.51600 0.00 0.00 35.53200+13.51600i
#> 2 36.38474 13.06610 0.02 0.02 36.38474+13.06610i
#> 3 37.21094 12.70009 0.04 0.04 37.21094+12.70009i
#> 4 37.98931 12.37357 0.06 0.06 37.98931+12.37357i
#> 5 38.97514 11.98246 0.08 0.08 38.97514+11.98246i
#> 6 39.91484 11.62190 0.10 0.10 39.91484+11.62190i
#> 7 40.89964 11.21677 0.12 0.12 40.89964+11.21677i
#> 8 41.54919 10.77190 0.14 0.14 41.54919+10.77190i
#> 9 42.26763 10.31796 0.16 0.16 42.26763+10.31796i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_2 Sim_7 TrajSim_2_7
#> 2 0.8527361-0.4498997i Traj_2 Sim_7 TrajSim_2_7
#> 3 0.8262047-0.3660113i Traj_2 Sim_7 TrajSim_2_7
#> 4 0.7783740-0.3265167i Traj_2 Sim_7 TrajSim_2_7
#> 5 0.9858237-0.3911154i Traj_2 Sim_7 TrajSim_2_7
#> 6 0.9397021-0.3605527i Traj_2 Sim_7 TrajSim_2_7
#> 7 0.9847954-0.4051351i Traj_2 Sim_7 TrajSim_2_7
#> 8 0.6495503-0.4448720i Traj_2 Sim_7 TrajSim_2_7
#> 9 0.7184443-0.4539321i Traj_2 Sim_7 TrajSim_2_7
#>
#> [[7]][[3]]
#> x y time displacementTime polar
#> 1 34.54800 14.10000 0.00 0.00 34.54800+14.10000i
#> 2 35.09796 15.30123 0.02 0.02 35.09796+15.30123i
#> 3 35.68486 16.45456 0.04 0.04 35.68486+16.45456i
#> 4 36.15872 17.44278 0.06 0.06 36.15872+17.44278i
#> 5 36.68471 18.32660 0.08 0.08 36.68471+18.32660i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_3 Sim_7 TrajSim_3_7
#> 2 0.5499557+1.2012303i Traj_3 Sim_7 TrajSim_3_7
#> 3 0.5869069+1.1533264i Traj_3 Sim_7 TrajSim_3_7
#> 4 0.4738617+0.9882235i Traj_3 Sim_7 TrajSim_3_7
#> 5 0.5259864+0.8838158i Traj_3 Sim_7 TrajSim_3_7
#>
#> [[7]][[4]]
#> x y time displacementTime polar
#> 1 32.26000 14.51800 0.00 0.00 32.26000+14.51800i
#> 2 31.24545 14.75995 0.02 0.02 31.24545+14.75995i
#> 3 30.23110 15.13256 0.04 0.04 30.23110+15.13256i
#> 4 29.19747 15.32622 0.06 0.06 29.19747+15.32622i
#> 5 28.21129 15.44034 0.08 0.08 28.21129+15.44034i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_4 Sim_7 TrajSim_4_7
#> 2 -1.0145483+0.2419475i Traj_4 Sim_7 TrajSim_4_7
#> 3 -1.0143540+0.3726121i Traj_4 Sim_7 TrajSim_4_7
#> 4 -1.0336300+0.1936634i Traj_4 Sim_7 TrajSim_4_7
#> 5 -0.9861732+0.1141137i Traj_4 Sim_7 TrajSim_4_7
#>
#> [[7]][[5]]
#> x y time displacementTime polar
#> 1 28.29000 13.57800 0.00 0.00 28.29000+13.57800i
#> 2 29.01418 13.16030 0.02 0.02 29.01418+13.16030i
#> 3 29.63501 12.76227 0.04 0.04 29.63501+12.76227i
#> 4 30.31729 12.32683 0.06 0.06 30.31729+12.32683i
#> 5 30.88830 11.83694 0.08 0.08 30.88830+11.83694i
#> 6 31.62901 11.16266 0.10 0.10 31.62901+11.16266i
#> 7 32.21468 10.43945 0.12 0.12 32.21468+10.43945i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_5 Sim_7 TrajSim_5_7
#> 2 0.7241795-0.4176966i Traj_5 Sim_7 TrajSim_5_7
#> 3 0.6208301-0.3980384i Traj_5 Sim_7 TrajSim_5_7
#> 4 0.6822825-0.4354382i Traj_5 Sim_7 TrajSim_5_7
#> 5 0.5710106-0.4898863i Traj_5 Sim_7 TrajSim_5_7
#> 6 0.7407109-0.6742787i Traj_5 Sim_7 TrajSim_5_7
#> 7 0.5856639-0.7232103i Traj_5 Sim_7 TrajSim_5_7
#>
#> [[7]][[6]]
#> x y time displacementTime polar
#> 1 26.19800 13.69800 0.00 0.00 26.19800+13.69800i
#> 2 25.12817 13.98044 0.02 0.02 25.12817+13.98044i
#> 3 24.06528 14.33057 0.04 0.04 24.06528+14.33057i
#> 4 22.89788 14.72843 0.06 0.06 22.89788+14.72843i
#> 5 21.92691 15.14148 0.08 0.08 21.92691+15.14148i
#> 6 20.81585 15.64991 0.10 0.10 20.81585+15.64991i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_6 Sim_7 TrajSim_6_7
#> 2 -1.0698277+0.2824403i Traj_6 Sim_7 TrajSim_6_7
#> 3 -1.0628935+0.3501328i Traj_6 Sim_7 TrajSim_6_7
#> 4 -1.1673970+0.3978532i Traj_6 Sim_7 TrajSim_6_7
#> 5 -0.9709684+0.4130521i Traj_6 Sim_7 TrajSim_6_7
#> 6 -1.1110611+0.5084313i Traj_6 Sim_7 TrajSim_6_7
#>
#> [[7]][[7]]
#> x y time displacementTime polar
#> 1 26.47200 15.49600 0.00 0.00 26.47200+15.49600i
#> 2 27.53442 14.95191 0.02 0.02 27.53442+14.95191i
#> 3 28.66731 14.27122 0.04 0.04 28.66731+14.27122i
#> 4 29.66316 13.65012 0.06 0.06 29.66316+13.65012i
#> 5 30.67598 12.98788 0.08 0.08 30.67598+12.98788i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_7 Sim_7 TrajSim_7_7
#> 2 1.0624214-0.5440874i Traj_7 Sim_7 TrajSim_7_7
#> 3 1.1328895-0.6806963i Traj_7 Sim_7 TrajSim_7_7
#> 4 0.9958523-0.6210969i Traj_7 Sim_7 TrajSim_7_7
#> 5 1.0128204-0.6622374i Traj_7 Sim_7 TrajSim_7_7
#>
#> [[7]][[8]]
#> x y time displacementTime polar
#> 1 13.21800 8.752000 0.00 0.00 13.21800+ 8.752000i
#> 2 13.52790 9.072075 0.02 0.02 13.52790+ 9.072075i
#> 3 13.78021 9.424782 0.04 0.04 13.78021+ 9.424782i
#> 4 13.96504 9.749243 0.06 0.06 13.96504+ 9.749243i
#> 5 14.16940 10.175752 0.08 0.08 14.16940+10.175752i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_8 Sim_7 TrajSim_8_7
#> 2 0.3099036+0.3200748i Traj_8 Sim_7 TrajSim_8_7
#> 3 0.2523096+0.3527069i Traj_8 Sim_7 TrajSim_8_7
#> 4 0.1848285+0.3244614i Traj_8 Sim_7 TrajSim_8_7
#> 5 0.2043576+0.4265093i Traj_8 Sim_7 TrajSim_8_7
#>
#> [[7]][[9]]
#> x y time displacementTime polar
#> 1 15.63800 8.164000 0.00 0.00 15.63800+ 8.164000i
#> 2 15.11058 8.889428 0.02 0.02 15.11058+ 8.889428i
#> 3 14.43866 9.661055 0.04 0.04 14.43866+ 9.661055i
#> 4 13.85545 10.506279 0.06 0.06 13.85545+10.506279i
#> 5 13.25497 11.363539 0.08 0.08 13.25497+11.363539i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_9 Sim_7 TrajSim_9_7
#> 2 -0.5274191+0.7254279i Traj_9 Sim_7 TrajSim_9_7
#> 3 -0.6719199+0.7716275i Traj_9 Sim_7 TrajSim_9_7
#> 4 -0.5832148+0.8452232i Traj_9 Sim_7 TrajSim_9_7
#> 5 -0.6004735+0.8572605i Traj_9 Sim_7 TrajSim_9_7
#>
#> [[7]][[10]]
#> x y time displacementTime polar
#> 1 14.69800 6.798000 0.00 0.00 14.69800+ 6.798000i
#> 2 15.17076 7.583395 0.02 0.02 15.17076+ 7.583395i
#> 3 15.72021 8.374158 0.04 0.04 15.72021+ 8.374158i
#> 4 16.27017 9.255054 0.06 0.06 16.27017+ 9.255054i
#> 5 16.84946 9.939739 0.08 0.08 16.84946+ 9.939739i
#> 6 17.37191 10.669089 0.10 0.10 17.37191+10.669089i
#> 7 17.85118 11.409199 0.12 0.12 17.85118+11.409199i
#> 8 18.28647 12.167849 0.14 0.14 18.28647+12.167849i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_10 Sim_7 TrajSim_10_7
#> 2 0.4727634+0.7853953i Traj_10 Sim_7 TrajSim_10_7
#> 3 0.5494454+0.7907624i Traj_10 Sim_7 TrajSim_10_7
#> 4 0.5499621+0.8808967i Traj_10 Sim_7 TrajSim_10_7
#> 5 0.5792924+0.6846844i Traj_10 Sim_7 TrajSim_10_7
#> 6 0.5224471+0.7293503i Traj_10 Sim_7 TrajSim_10_7
#> 7 0.4792648+0.7401098i Traj_10 Sim_7 TrajSim_10_7
#> 8 0.4352929+0.7586506i Traj_10 Sim_7 TrajSim_10_7
#>
#> [[7]][[11]]
#> x y time displacementTime polar
#> 1 12.00600 7.316000 0.00 0.00 12.00600+7.316000i
#> 2 11.80112 6.117651 0.02 0.02 11.80112+6.117651i
#> 3 11.56789 5.116597 0.04 0.04 11.56789+5.116597i
#> 4 11.42528 3.969206 0.06 0.06 11.42528+3.969206i
#> 5 11.30704 3.056892 0.08 0.08 11.30704+3.056892i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_11 Sim_7 TrajSim_11_7
#> 2 -0.2048812-1.1983493i Traj_11 Sim_7 TrajSim_11_7
#> 3 -0.2332309-1.0010542i Traj_11 Sim_7 TrajSim_11_7
#> 4 -0.1426034-1.1473907i Traj_11 Sim_7 TrajSim_11_7
#> 5 -0.1182395-0.9123135i Traj_11 Sim_7 TrajSim_11_7
#>
#>
#> [[8]]
#> [[8]][[1]]
#> x y time displacementTime polar
#> 1 36.88200 14.05600 0.00 0.00 36.88200+14.05600i
#> 2 36.03259 14.23245 0.02 0.02 36.03259+14.23245i
#> 3 35.29692 14.43986 0.04 0.04 35.29692+14.43986i
#> 4 34.47543 14.64884 0.06 0.06 34.47543+14.64884i
#> 5 33.60837 14.89593 0.08 0.08 33.60837+14.89593i
#> 6 32.81755 15.26919 0.10 0.10 32.81755+15.26919i
#> 7 31.96112 15.73568 0.12 0.12 31.96112+15.73568i
#> 8 31.15001 16.16422 0.14 0.14 31.15001+16.16422i
#> 9 30.33391 16.65923 0.16 0.16 30.33391+16.65923i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_1 Sim_8 TrajSim_1_8
#> 2 -0.8494118+0.1764482i Traj_1 Sim_8 TrajSim_1_8
#> 3 -0.7356714+0.2074118i Traj_1 Sim_8 TrajSim_1_8
#> 4 -0.8214893+0.2089784i Traj_1 Sim_8 TrajSim_1_8
#> 5 -0.8670530+0.2470881i Traj_1 Sim_8 TrajSim_1_8
#> 6 -0.7908216+0.3732639i Traj_1 Sim_8 TrajSim_1_8
#> 7 -0.8564298+0.4664879i Traj_1 Sim_8 TrajSim_1_8
#> 8 -0.8111118+0.4285426i Traj_1 Sim_8 TrajSim_1_8
#> 9 -0.8160994+0.4950131i Traj_1 Sim_8 TrajSim_1_8
#>
#> [[8]][[2]]
#> x y time displacementTime polar
#> 1 35.53200 13.51600 0.00 0.00 35.53200+13.51600i
#> 2 36.32770 14.09532 0.02 0.02 36.32770+14.09532i
#> 3 37.07614 14.63059 0.04 0.04 37.07614+14.63059i
#> 4 37.76507 15.11334 0.06 0.06 37.76507+15.11334i
#> 5 38.49323 15.64692 0.08 0.08 38.49323+15.64692i
#> 6 39.27429 16.27112 0.10 0.10 39.27429+16.27112i
#> 7 40.03836 16.86775 0.12 0.12 40.03836+16.86775i
#> 8 40.69179 17.43335 0.14 0.14 40.69179+17.43335i
#> 9 41.34093 18.05118 0.16 0.16 41.34093+18.05118i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_2 Sim_8 TrajSim_2_8
#> 2 0.7956989+0.5793248i Traj_2 Sim_8 TrajSim_2_8
#> 3 0.7484396+0.5352651i Traj_2 Sim_8 TrajSim_2_8
#> 4 0.6889364+0.4827491i Traj_2 Sim_8 TrajSim_2_8
#> 5 0.7281561+0.5335814i Traj_2 Sim_8 TrajSim_2_8
#> 6 0.7810619+0.6242023i Traj_2 Sim_8 TrajSim_2_8
#> 7 0.7640672+0.5966223i Traj_2 Sim_8 TrajSim_2_8
#> 8 0.6534291+0.5656035i Traj_2 Sim_8 TrajSim_2_8
#> 9 0.6491422+0.6178350i Traj_2 Sim_8 TrajSim_2_8
#>
#> [[8]][[3]]
#> x y time displacementTime polar
#> 1 34.54800 14.10000 0.00 0.00 34.54800+14.10000i
#> 2 33.58792 14.33120 0.02 0.02 33.58792+14.33120i
#> 3 32.56587 14.57466 0.04 0.04 32.56587+14.57466i
#> 4 31.35031 14.83814 0.06 0.06 31.35031+14.83814i
#> 5 30.36056 15.07333 0.08 0.08 30.36056+15.07333i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_3 Sim_8 TrajSim_3_8
#> 2 -0.9600827+0.2311957i Traj_3 Sim_8 TrajSim_3_8
#> 3 -1.0220456+0.2434681i Traj_3 Sim_8 TrajSim_3_8
#> 4 -1.2155597+0.2634747i Traj_3 Sim_8 TrajSim_3_8
#> 5 -0.9897487+0.2351923i Traj_3 Sim_8 TrajSim_3_8
#>
#> [[8]][[4]]
#> x y time displacementTime polar
#> 1 32.26000 14.51800 0.00 0.00 32.26000+14.51800i
#> 2 33.16926 13.99642 0.02 0.02 33.16926+13.99642i
#> 3 33.93943 13.40534 0.04 0.04 33.93943+13.40534i
#> 4 34.84086 12.88145 0.06 0.06 34.84086+12.88145i
#> 5 35.67713 12.27427 0.08 0.08 35.67713+12.27427i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_4 Sim_8 TrajSim_4_8
#> 2 0.9092575-0.5215751i Traj_4 Sim_8 TrajSim_4_8
#> 3 0.7701678-0.5910862i Traj_4 Sim_8 TrajSim_4_8
#> 4 0.9014343-0.5238918i Traj_4 Sim_8 TrajSim_4_8
#> 5 0.8362677-0.6071784i Traj_4 Sim_8 TrajSim_4_8
#>
#> [[8]][[5]]
#> x y time displacementTime polar
#> 1 28.29000 13.57800 0.00 0.00 28.29000+13.57800i
#> 2 29.17973 13.32425 0.02 0.02 29.17973+13.32425i
#> 3 30.05281 13.21811 0.04 0.04 30.05281+13.21811i
#> 4 30.76896 13.05346 0.06 0.06 30.76896+13.05346i
#> 5 31.67741 12.89069 0.08 0.08 31.67741+12.89069i
#> 6 32.56351 12.74268 0.10 0.10 32.56351+12.74268i
#> 7 33.20360 12.52870 0.12 0.12 33.20360+12.52870i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_5 Sim_8 TrajSim_5_8
#> 2 0.8897268-0.2537520i Traj_5 Sim_8 TrajSim_5_8
#> 3 0.8730825-0.1061382i Traj_5 Sim_8 TrajSim_5_8
#> 4 0.7161503-0.1646469i Traj_5 Sim_8 TrajSim_5_8
#> 5 0.9084502-0.1627772i Traj_5 Sim_8 TrajSim_5_8
#> 6 0.8861006-0.1480041i Traj_5 Sim_8 TrajSim_5_8
#> 7 0.6400913-0.2139828i Traj_5 Sim_8 TrajSim_5_8
#>
#> [[8]][[6]]
#> x y time displacementTime polar
#> 1 26.19800 13.69800 0.00 0.00 26.19800+13.69800i
#> 2 26.13706 14.66893 0.02 0.02 26.13706+14.66893i
#> 3 26.03288 15.62932 0.04 0.04 26.03288+15.62932i
#> 4 25.88458 16.65618 0.06 0.06 25.88458+16.65618i
#> 5 25.79387 17.78992 0.08 0.08 25.79387+17.78992i
#> 6 25.65979 18.85651 0.10 0.10 25.65979+18.85651i
#> displacement Trajectory Simulation TrajSim
#> 1 0.00000000+0.0000000i Traj_6 Sim_8 TrajSim_6_8
#> 2 -0.06093887+0.9709331i Traj_6 Sim_8 TrajSim_6_8
#> 3 -0.10417913+0.9603917i Traj_6 Sim_8 TrajSim_6_8
#> 4 -0.14830645+1.0268588i Traj_6 Sim_8 TrajSim_6_8
#> 5 -0.09070608+1.1337380i Traj_6 Sim_8 TrajSim_6_8
#> 6 -0.13408280+1.0665904i Traj_6 Sim_8 TrajSim_6_8
#>
#> [[8]][[7]]
#> x y time displacementTime polar
#> 1 26.47200 15.49600 0.00 0.00 26.47200+15.49600i
#> 2 27.19634 16.18120 0.02 0.02 27.19634+16.18120i
#> 3 27.98089 16.89808 0.04 0.04 27.98089+16.89808i
#> 4 28.85137 17.65847 0.06 0.06 28.85137+17.65847i
#> 5 29.90382 18.65837 0.08 0.08 29.90382+18.65837i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_7 Sim_8 TrajSim_7_8
#> 2 0.7243446+0.6852012i Traj_7 Sim_8 TrajSim_7_8
#> 3 0.7845464+0.7168783i Traj_7 Sim_8 TrajSim_7_8
#> 4 0.8704801+0.7603887i Traj_7 Sim_8 TrajSim_7_8
#> 5 1.0524459+0.9999024i Traj_7 Sim_8 TrajSim_7_8
#>
#> [[8]][[8]]
#> x y time displacementTime polar
#> 1 13.21800 8.752000 0.00 0.00 13.21800+8.752000i
#> 2 13.57950 8.690494 0.02 0.02 13.57950+8.690494i
#> 3 13.97566 8.577908 0.04 0.04 13.97566+8.577908i
#> 4 14.39154 8.546693 0.06 0.06 14.39154+8.546693i
#> 5 14.83365 8.465172 0.08 0.08 14.83365+8.465172i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.00000000i Traj_8 Sim_8 TrajSim_8_8
#> 2 0.3614982-0.06150559i Traj_8 Sim_8 TrajSim_8_8
#> 3 0.3961665-0.11258637i Traj_8 Sim_8 TrajSim_8_8
#> 4 0.4158754-0.03121502i Traj_8 Sim_8 TrajSim_8_8
#> 5 0.4421051-0.08152061i Traj_8 Sim_8 TrajSim_8_8
#>
#> [[8]][[9]]
#> x y time displacementTime polar
#> 1 15.63800 8.164000 0.00 0.00 15.63800+ 8.164000i
#> 2 16.14655 9.041739 0.02 0.02 16.14655+ 9.041739i
#> 3 16.70162 9.881060 0.04 0.04 16.70162+ 9.881060i
#> 4 17.38152 10.678529 0.06 0.06 17.38152+10.678529i
#> 5 17.93847 11.574504 0.08 0.08 17.93847+11.574504i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_9 Sim_8 TrajSim_9_8
#> 2 0.5085454+0.8777392i Traj_9 Sim_8 TrajSim_9_8
#> 3 0.5550789+0.8393213i Traj_9 Sim_8 TrajSim_9_8
#> 4 0.6798926+0.7974688i Traj_9 Sim_8 TrajSim_9_8
#> 5 0.5569523+0.8959750i Traj_9 Sim_8 TrajSim_9_8
#>
#> [[8]][[10]]
#> x y time displacementTime polar
#> 1 14.69800 6.798000 0.00 0.00 14.69800+ 6.798000i
#> 2 14.05899 7.628706 0.02 0.02 14.05899+ 7.628706i
#> 3 13.58343 8.303031 0.04 0.04 13.58343+ 8.303031i
#> 4 13.05804 9.041294 0.06 0.06 13.05804+ 9.041294i
#> 5 12.45488 9.770458 0.08 0.08 12.45488+ 9.770458i
#> 6 11.85103 10.366084 0.10 0.10 11.85103+10.366084i
#> 7 11.20458 11.038296 0.12 0.12 11.20458+11.038296i
#> 8 10.59231 11.692997 0.14 0.14 10.59231+11.692997i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_10 Sim_8 TrajSim_10_8
#> 2 -0.6390069+0.8307063i Traj_10 Sim_8 TrajSim_10_8
#> 3 -0.4755653+0.6743244i Traj_10 Sim_8 TrajSim_10_8
#> 4 -0.5253918+0.7382632i Traj_10 Sim_8 TrajSim_10_8
#> 5 -0.6031521+0.7291641i Traj_10 Sim_8 TrajSim_10_8
#> 6 -0.6038539+0.5956258i Traj_10 Sim_8 TrajSim_10_8
#> 7 -0.6464468+0.6722122i Traj_10 Sim_8 TrajSim_10_8
#> 8 -0.6122767+0.6547008i Traj_10 Sim_8 TrajSim_10_8
#>
#> [[8]][[11]]
#> x y time displacementTime polar
#> 1 12.00600 7.316000 0.00 0.00 12.00600+ 7.316000i
#> 2 11.72264 8.400658 0.02 0.02 11.72264+ 8.400658i
#> 3 11.40295 9.414216 0.04 0.04 11.40295+ 9.414216i
#> 4 11.13439 10.457833 0.06 0.06 11.13439+10.457833i
#> 5 10.86660 11.461097 0.08 0.08 10.86660+11.461097i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.000000i Traj_11 Sim_8 TrajSim_11_8
#> 2 -0.2833583+1.084658i Traj_11 Sim_8 TrajSim_11_8
#> 3 -0.3196946+1.013558i Traj_11 Sim_8 TrajSim_11_8
#> 4 -0.2685563+1.043618i Traj_11 Sim_8 TrajSim_11_8
#> 5 -0.2677893+1.003264i Traj_11 Sim_8 TrajSim_11_8
#>
#>
#> [[9]]
#> [[9]][[1]]
#> x y time displacementTime polar
#> 1 36.88200 14.05600 0.00 0.00 36.88200+14.05600i
#> 2 35.94032 14.42892 0.02 0.02 35.94032+14.42892i
#> 3 35.06160 14.77494 0.04 0.04 35.06160+14.77494i
#> 4 34.18265 15.20236 0.06 0.06 34.18265+15.20236i
#> 5 33.44979 15.62967 0.08 0.08 33.44979+15.62967i
#> 6 32.57020 16.09815 0.10 0.10 32.57020+16.09815i
#> 7 31.78355 16.38955 0.12 0.12 31.78355+16.38955i
#> 8 30.88853 16.67487 0.14 0.14 30.88853+16.67487i
#> 9 30.02091 16.93040 0.16 0.16 30.02091+16.93040i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_1 Sim_9 TrajSim_1_9
#> 2 -0.9416777+0.3729178i Traj_1 Sim_9 TrajSim_1_9
#> 3 -0.8787178+0.3460224i Traj_1 Sim_9 TrajSim_1_9
#> 4 -0.8789561+0.4274162i Traj_1 Sim_9 TrajSim_1_9
#> 5 -0.7328607+0.4273094i Traj_1 Sim_9 TrajSim_1_9
#> 6 -0.8795903+0.4684804i Traj_1 Sim_9 TrajSim_1_9
#> 7 -0.7866434+0.2914080i Traj_1 Sim_9 TrajSim_1_9
#> 8 -0.8950273+0.2853131i Traj_1 Sim_9 TrajSim_1_9
#> 9 -0.8676140+0.2555364i Traj_1 Sim_9 TrajSim_1_9
#>
#> [[9]][[2]]
#> x y time displacementTime polar
#> 1 35.53200 13.51600 0.00 0.00 35.53200+13.51600i
#> 2 34.68623 13.46326 0.02 0.02 34.68623+13.46326i
#> 3 33.57945 13.41979 0.04 0.04 33.57945+13.41979i
#> 4 32.62147 13.49714 0.06 0.06 32.62147+13.49714i
#> 5 31.68714 13.58687 0.08 0.08 31.68714+13.58687i
#> 6 30.74342 13.64679 0.10 0.10 30.74342+13.64679i
#> 7 29.79107 13.62682 0.12 0.12 29.79107+13.62682i
#> 8 28.83420 13.57496 0.14 0.14 28.83420+13.57496i
#> 9 27.90167 13.52580 0.16 0.16 27.90167+13.52580i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.00000000i Traj_2 Sim_9 TrajSim_2_9
#> 2 -0.8457674-0.05274156i Traj_2 Sim_9 TrajSim_2_9
#> 3 -1.1067805-0.04347338i Traj_2 Sim_9 TrajSim_2_9
#> 4 -0.9579863+0.07735593i Traj_2 Sim_9 TrajSim_2_9
#> 5 -0.9343230+0.08973137i Traj_2 Sim_9 TrajSim_2_9
#> 6 -0.9437235+0.05991354i Traj_2 Sim_9 TrajSim_2_9
#> 7 -0.9523443-0.01997013i Traj_2 Sim_9 TrajSim_2_9
#> 8 -0.9568764-0.05185305i Traj_2 Sim_9 TrajSim_2_9
#> 9 -0.9325265-0.04916677i Traj_2 Sim_9 TrajSim_2_9
#>
#> [[9]][[3]]
#> x y time displacementTime polar
#> 1 34.54800 14.10000 0.00 0.00 34.54800+14.10000i
#> 2 34.61481 15.19975 0.02 0.02 34.61481+15.19975i
#> 3 34.69301 16.40500 0.04 0.04 34.69301+16.40500i
#> 4 34.75291 17.45631 0.06 0.06 34.75291+17.45631i
#> 5 34.82251 18.42834 0.08 0.08 34.82251+18.42834i
#> displacement Trajectory Simulation TrajSim
#> 1 0.00000000+0.0000000i Traj_3 Sim_9 TrajSim_3_9
#> 2 0.06681166+1.0997518i Traj_3 Sim_9 TrajSim_3_9
#> 3 0.07819674+1.2052448i Traj_3 Sim_9 TrajSim_3_9
#> 4 0.05990404+1.0513103i Traj_3 Sim_9 TrajSim_3_9
#> 5 0.06959635+0.9720365i Traj_3 Sim_9 TrajSim_3_9
#>
#> [[9]][[4]]
#> x y time displacementTime polar
#> 1 32.26000 14.51800 0.00 0.00 32.26000+14.51800i
#> 2 31.27849 14.87949 0.02 0.02 31.27849+14.87949i
#> 3 30.35514 15.24851 0.04 0.04 30.35514+15.24851i
#> 4 29.47884 15.64779 0.06 0.06 29.47884+15.64779i
#> 5 28.49514 16.24959 0.08 0.08 28.49514+16.24959i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_4 Sim_9 TrajSim_4_9
#> 2 -0.9815122+0.3614879i Traj_4 Sim_9 TrajSim_4_9
#> 3 -0.9233480+0.3690182i Traj_4 Sim_9 TrajSim_4_9
#> 4 -0.8762995+0.3992877i Traj_4 Sim_9 TrajSim_4_9
#> 5 -0.9837020+0.6017948i Traj_4 Sim_9 TrajSim_4_9
#>
#> [[9]][[5]]
#> x y time displacementTime polar
#> 1 28.29000 13.57800 0.00 0.00 28.29000+13.57800i
#> 2 27.60828 14.25369 0.02 0.02 27.60828+14.25369i
#> 3 27.03526 14.88880 0.04 0.04 27.03526+14.88880i
#> 4 26.39923 15.49006 0.06 0.06 26.39923+15.49006i
#> 5 25.82992 16.17012 0.08 0.08 25.82992+16.17012i
#> 6 25.36060 16.78538 0.10 0.10 25.36060+16.78538i
#> 7 24.74862 17.56431 0.12 0.12 24.74862+17.56431i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_5 Sim_9 TrajSim_5_9
#> 2 -0.6817243+0.6756877i Traj_5 Sim_9 TrajSim_5_9
#> 3 -0.5730107+0.6351078i Traj_5 Sim_9 TrajSim_5_9
#> 4 -0.6360316+0.6012692i Traj_5 Sim_9 TrajSim_5_9
#> 5 -0.5693089+0.6800512i Traj_5 Sim_9 TrajSim_5_9
#> 6 -0.4693290+0.6152634i Traj_5 Sim_9 TrajSim_5_9
#> 7 -0.6119784+0.7789330i Traj_5 Sim_9 TrajSim_5_9
#>
#> [[9]][[6]]
#> x y time displacementTime polar
#> 1 26.19800 13.69800 0.00 0.00 26.19800+13.69800i
#> 2 25.98848 14.76208 0.02 0.02 25.98848+14.76208i
#> 3 25.71071 15.74612 0.04 0.04 25.71071+15.74612i
#> 4 25.48391 16.73653 0.06 0.06 25.48391+16.73653i
#> 5 25.35132 17.77976 0.08 0.08 25.35132+17.77976i
#> 6 25.29822 18.88102 0.10 0.10 25.29822+18.88102i
#> displacement Trajectory Simulation TrajSim
#> 1 0.00000000+0.0000000i Traj_6 Sim_9 TrajSim_6_9
#> 2 -0.20952101+1.0640846i Traj_6 Sim_9 TrajSim_6_9
#> 3 -0.27777279+0.9840372i Traj_6 Sim_9 TrajSim_6_9
#> 4 -0.22679992+0.9904105i Traj_6 Sim_9 TrajSim_6_9
#> 5 -0.13258229+1.0432295i Traj_6 Sim_9 TrajSim_6_9
#> 6 -0.05310342+1.1012577i Traj_6 Sim_9 TrajSim_6_9
#>
#> [[9]][[7]]
#> x y time displacementTime polar
#> 1 26.47200 15.49600 0.00 0.00 26.47200+15.49600i
#> 2 25.86935 16.64021 0.02 0.02 25.86935+16.64021i
#> 3 25.36307 18.04472 0.04 0.04 25.36307+18.04472i
#> 4 24.89983 19.16549 0.06 0.06 24.89983+19.16549i
#> 5 24.36741 20.53484 0.08 0.08 24.36741+20.53484i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.000000i Traj_7 Sim_9 TrajSim_7_9
#> 2 -0.6026486+1.144214i Traj_7 Sim_9 TrajSim_7_9
#> 3 -0.5062835+1.404508i Traj_7 Sim_9 TrajSim_7_9
#> 4 -0.4632407+1.120772i Traj_7 Sim_9 TrajSim_7_9
#> 5 -0.5324199+1.369345i Traj_7 Sim_9 TrajSim_7_9
#>
#> [[9]][[8]]
#> x y time displacementTime polar
#> 1 13.21800 8.752000 0.00 0.00 13.21800+ 8.752000i
#> 2 13.50094 9.073642 0.02 0.02 13.50094+ 9.073642i
#> 3 13.64690 9.464740 0.04 0.04 13.64690+ 9.464740i
#> 4 13.78131 9.831196 0.06 0.06 13.78131+ 9.831196i
#> 5 13.92104 10.231184 0.08 0.08 13.92104+10.231184i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_8 Sim_9 TrajSim_8_9
#> 2 0.2829431+0.3216420i Traj_8 Sim_9 TrajSim_8_9
#> 3 0.1459524+0.3910975i Traj_8 Sim_9 TrajSim_8_9
#> 4 0.1344150+0.3664568i Traj_8 Sim_9 TrajSim_8_9
#> 5 0.1397256+0.3999878i Traj_8 Sim_9 TrajSim_8_9
#>
#> [[9]][[9]]
#> x y time displacementTime polar
#> 1 15.63800 8.164000 0.00 0.00 15.63800+8.164000i
#> 2 16.66568 8.304055 0.02 0.02 16.66568+8.304055i
#> 3 17.65957 8.699328 0.04 0.04 17.65957+8.699328i
#> 4 18.63933 9.088139 0.06 0.06 18.63933+9.088139i
#> 5 19.60605 9.449804 0.08 0.08 19.60605+9.449804i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_9 Sim_9 TrajSim_9_9
#> 2 1.0276791+0.1400546i Traj_9 Sim_9 TrajSim_9_9
#> 3 0.9938894+0.3952730i Traj_9 Sim_9 TrajSim_9_9
#> 4 0.9797565+0.3888115i Traj_9 Sim_9 TrajSim_9_9
#> 5 0.9667275+0.3616645i Traj_9 Sim_9 TrajSim_9_9
#>
#> [[9]][[10]]
#> x y time displacementTime polar
#> 1 14.69800 6.798000 0.00 0.00 14.69800+ 6.798000i
#> 2 15.07885 7.629430 0.02 0.02 15.07885+ 7.629430i
#> 3 15.37367 8.572632 0.04 0.04 15.37367+ 8.572632i
#> 4 15.75009 9.474579 0.06 0.06 15.75009+ 9.474579i
#> 5 16.16223 10.253755 0.08 0.08 16.16223+10.253755i
#> 6 16.54204 11.016221 0.10 0.10 16.54204+11.016221i
#> 7 16.93714 11.775960 0.12 0.12 16.93714+11.775960i
#> 8 17.38066 12.654153 0.14 0.14 17.38066+12.654153i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_10 Sim_9 TrajSim_10_9
#> 2 0.3808485+0.8314295i Traj_10 Sim_9 TrajSim_10_9
#> 3 0.2948165+0.9432023i Traj_10 Sim_9 TrajSim_10_9
#> 4 0.3764229+0.9019474i Traj_10 Sim_9 TrajSim_10_9
#> 5 0.4121411+0.7791753i Traj_10 Sim_9 TrajSim_10_9
#> 6 0.3798089+0.7624663i Traj_10 Sim_9 TrajSim_10_9
#> 7 0.3951051+0.7597395i Traj_10 Sim_9 TrajSim_10_9
#> 8 0.4435153+0.8781927i Traj_10 Sim_9 TrajSim_10_9
#>
#> [[9]][[11]]
#> x y time displacementTime polar
#> 1 12.00600 7.316000 0.00 0.00 12.00600+7.316000i
#> 2 11.83228 6.287181 0.02 0.02 11.83228+6.287181i
#> 3 11.66546 5.197199 0.04 0.04 11.66546+5.197199i
#> 4 11.57905 4.076839 0.06 0.06 11.57905+4.076839i
#> 5 11.55545 2.953868 0.08 0.08 11.55545+2.953868i
#> displacement Trajectory Simulation TrajSim
#> 1 0.00000000+0.000000i Traj_11 Sim_9 TrajSim_11_9
#> 2 -0.17371554-1.028819i Traj_11 Sim_9 TrajSim_11_9
#> 3 -0.16682552-1.089982i Traj_11 Sim_9 TrajSim_11_9
#> 4 -0.08640543-1.120360i Traj_11 Sim_9 TrajSim_11_9
#> 5 -0.02360226-1.122972i Traj_11 Sim_9 TrajSim_11_9
#>
#>
#> [[10]]
#> [[10]][[1]]
#> x y time displacementTime polar
#> 1 36.88200 14.05600 0.00 0.00 36.88200+14.05600i
#> 2 36.00500 13.99945 0.02 0.02 36.00500+13.99945i
#> 3 35.21393 13.90496 0.04 0.04 35.21393+13.90496i
#> 4 34.26796 13.78414 0.06 0.06 34.26796+13.78414i
#> 5 33.35297 13.72021 0.08 0.08 33.35297+13.72021i
#> 6 32.44475 13.69188 0.10 0.10 32.44475+13.69188i
#> 7 31.58896 13.66048 0.12 0.12 31.58896+13.66048i
#> 8 30.68942 13.62920 0.14 0.14 30.68942+13.62920i
#> 9 29.81777 13.61700 0.16 0.16 29.81777+13.61700i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.00000000i Traj_1 Sim_10 TrajSim_1_10
#> 2 -0.8770009-0.05655135i Traj_1 Sim_10 TrajSim_1_10
#> 3 -0.7910650-0.09449251i Traj_1 Sim_10 TrajSim_1_10
#> 4 -0.9459714-0.12081631i Traj_1 Sim_10 TrajSim_1_10
#> 5 -0.9149918-0.06393369i Traj_1 Sim_10 TrajSim_1_10
#> 6 -0.9082243-0.02832904i Traj_1 Sim_10 TrajSim_1_10
#> 7 -0.8557875-0.03139845i Traj_1 Sim_10 TrajSim_1_10
#> 8 -0.8995372-0.03127836i Traj_1 Sim_10 TrajSim_1_10
#> 9 -0.8716557-0.01220443i Traj_1 Sim_10 TrajSim_1_10
#>
#> [[10]][[2]]
#> x y time displacementTime polar
#> 1 35.53200 13.51600 0.00 0.00 35.53200+13.51600i
#> 2 34.71637 13.77444 0.02 0.02 34.71637+13.77444i
#> 3 33.97849 14.20359 0.04 0.04 33.97849+14.20359i
#> 4 33.13549 14.80573 0.06 0.06 33.13549+14.80573i
#> 5 32.38444 15.38917 0.08 0.08 32.38444+15.38917i
#> 6 31.57375 15.95658 0.10 0.10 31.57375+15.95658i
#> 7 30.82235 16.49214 0.12 0.12 30.82235+16.49214i
#> 8 29.98437 17.03978 0.14 0.14 29.98437+17.03978i
#> 9 29.19826 17.54542 0.16 0.16 29.19826+17.54542i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_2 Sim_10 TrajSim_2_10
#> 2 -0.8156331+0.2584425i Traj_2 Sim_10 TrajSim_2_10
#> 3 -0.7378760+0.4291521i Traj_2 Sim_10 TrajSim_2_10
#> 4 -0.8429989+0.6021322i Traj_2 Sim_10 TrajSim_2_10
#> 5 -0.7510518+0.5834402i Traj_2 Sim_10 TrajSim_2_10
#> 6 -0.8106918+0.5674149i Traj_2 Sim_10 TrajSim_2_10
#> 7 -0.7513968+0.5355565i Traj_2 Sim_10 TrajSim_2_10
#> 8 -0.8379804+0.5476404i Traj_2 Sim_10 TrajSim_2_10
#> 9 -0.7861138+0.5056369i Traj_2 Sim_10 TrajSim_2_10
#>
#> [[10]][[3]]
#> x y time displacementTime polar
#> 1 34.54800 14.10000 0.00 0.00 34.54800+14.10000i
#> 2 35.72716 14.32401 0.02 0.02 35.72716+14.32401i
#> 3 36.81818 14.42259 0.04 0.04 36.81818+14.42259i
#> 4 37.81175 14.54138 0.06 0.06 37.81175+14.54138i
#> 5 39.02649 14.72663 0.08 0.08 39.02649+14.72663i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.00000000i Traj_3 Sim_10 TrajSim_3_10
#> 2 1.1791583+0.22401356i Traj_3 Sim_10 TrajSim_3_10
#> 3 1.0910261+0.09857524i Traj_3 Sim_10 TrajSim_3_10
#> 4 0.9935684+0.11879304i Traj_3 Sim_10 TrajSim_3_10
#> 5 1.2147374+0.18525034i Traj_3 Sim_10 TrajSim_3_10
#>
#> [[10]][[4]]
#> x y time displacementTime polar
#> 1 32.26000 14.51800 0.00 0.00 32.26000+14.51800i
#> 2 33.11851 14.16969 0.02 0.02 33.11851+14.16969i
#> 3 33.90460 13.65767 0.04 0.04 33.90460+13.65767i
#> 4 34.80074 13.19069 0.06 0.06 34.80074+13.19069i
#> 5 35.62556 12.75472 0.08 0.08 35.62556+12.75472i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_4 Sim_10 TrajSim_4_10
#> 2 0.8585105-0.3483074i Traj_4 Sim_10 TrajSim_4_10
#> 3 0.7860935-0.5120212i Traj_4 Sim_10 TrajSim_4_10
#> 4 0.8961327-0.4669794i Traj_4 Sim_10 TrajSim_4_10
#> 5 0.8248231-0.4359733i Traj_4 Sim_10 TrajSim_4_10
#>
#> [[10]][[5]]
#> x y time displacementTime polar
#> 1 28.29000 13.57800 0.00 0.00 28.29000+13.57800i
#> 2 27.46236 13.51182 0.02 0.02 27.46236+13.51182i
#> 3 26.62187 13.51710 0.04 0.04 26.62187+13.51710i
#> 4 25.88383 13.51500 0.06 0.06 25.88383+13.51500i
#> 5 25.10592 13.54357 0.08 0.08 25.10592+13.54357i
#> 6 24.17814 13.42257 0.10 0.10 24.17814+13.42257i
#> 7 23.19984 13.33976 0.12 0.12 23.19984+13.33976i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.000000000i Traj_5 Sim_10 TrajSim_5_10
#> 2 -0.8276393-0.066179641i Traj_5 Sim_10 TrajSim_5_10
#> 3 -0.8404949+0.005280357i Traj_5 Sim_10 TrajSim_5_10
#> 4 -0.7380316-0.002097396i Traj_5 Sim_10 TrajSim_5_10
#> 5 -0.7779102+0.028570385i Traj_5 Sim_10 TrajSim_5_10
#> 6 -0.9277807-0.121005617i Traj_5 Sim_10 TrajSim_5_10
#> 7 -0.9783079-0.082803973i Traj_5 Sim_10 TrajSim_5_10
#>
#> [[10]][[6]]
#> x y time displacementTime polar
#> 1 26.19800 13.69800 0.00 0.00 26.19800+13.69800i
#> 2 25.28828 13.03044 0.02 0.02 25.28828+13.03044i
#> 3 24.21621 12.51950 0.04 0.04 24.21621+12.51950i
#> 4 23.09542 12.09358 0.06 0.06 23.09542+12.09358i
#> 5 22.05358 11.88234 0.08 0.08 22.05358+11.88234i
#> 6 21.04321 11.60520 0.10 0.10 21.04321+11.60520i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_6 Sim_10 TrajSim_6_10
#> 2 -0.9097157-0.6675626i Traj_6 Sim_10 TrajSim_6_10
#> 3 -1.0720763-0.5109359i Traj_6 Sim_10 TrajSim_6_10
#> 4 -1.1207926-0.4259249i Traj_6 Sim_10 TrajSim_6_10
#> 5 -1.0418345-0.2112377i Traj_6 Sim_10 TrajSim_6_10
#> 6 -1.0103681-0.2771380i Traj_6 Sim_10 TrajSim_6_10
#>
#> [[10]][[7]]
#> x y time displacementTime polar
#> 1 26.47200 15.49600 0.00 0.00 26.47200+15.49600i
#> 2 26.19503 16.78730 0.02 0.02 26.19503+16.78730i
#> 3 26.05602 17.73886 0.04 0.04 26.05602+17.73886i
#> 4 25.84796 18.85566 0.06 0.06 25.84796+18.85566i
#> 5 25.67285 19.94146 0.08 0.08 25.67285+19.94146i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_7 Sim_10 TrajSim_7_10
#> 2 -0.2769729+1.2912988i Traj_7 Sim_10 TrajSim_7_10
#> 3 -0.1390099+0.9515596i Traj_7 Sim_10 TrajSim_7_10
#> 4 -0.2080592+1.1168033i Traj_7 Sim_10 TrajSim_7_10
#> 5 -0.1751115+1.0858026i Traj_7 Sim_10 TrajSim_7_10
#>
#> [[10]][[8]]
#> x y time displacementTime polar
#> 1 13.21800 8.752000 0.00 0.00 13.21800+8.752000i
#> 2 13.65108 8.661898 0.02 0.02 13.65108+8.661898i
#> 3 14.09646 8.522600 0.04 0.04 14.09646+8.522600i
#> 4 14.48691 8.405852 0.06 0.06 14.48691+8.405852i
#> 5 14.90509 8.336996 0.08 0.08 14.90509+8.336996i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.00000000i Traj_8 Sim_10 TrajSim_8_10
#> 2 0.4330777-0.09010164i Traj_8 Sim_10 TrajSim_8_10
#> 3 0.4453788-0.13929871i Traj_8 Sim_10 TrajSim_8_10
#> 4 0.3904565-0.11674775i Traj_8 Sim_10 TrajSim_8_10
#> 5 0.4181802-0.06885589i Traj_8 Sim_10 TrajSim_8_10
#>
#> [[10]][[9]]
#> x y time displacementTime polar
#> 1 15.63800 8.164000 0.00 0.00 15.63800+8.164000i
#> 2 14.70969 7.627399 0.02 0.02 14.70969+7.627399i
#> 3 13.80300 7.041389 0.04 0.04 13.80300+7.041389i
#> 4 12.86669 6.497123 0.06 0.06 12.86669+6.497123i
#> 5 11.94873 5.955742 0.08 0.08 11.94873+5.955742i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_9 Sim_10 TrajSim_9_10
#> 2 -0.9283127-0.5366011i Traj_9 Sim_10 TrajSim_9_10
#> 3 -0.9066899-0.5860099i Traj_9 Sim_10 TrajSim_9_10
#> 4 -0.9363084-0.5442663i Traj_9 Sim_10 TrajSim_9_10
#> 5 -0.9179593-0.5413806i Traj_9 Sim_10 TrajSim_9_10
#>
#> [[10]][[10]]
#> x y time displacementTime polar
#> 1 14.69800 6.798000 0.00 0.00 14.69800+ 6.798000i
#> 2 14.11347 7.450844 0.02 0.02 14.11347+ 7.450844i
#> 3 13.44839 8.078428 0.04 0.04 13.44839+ 8.078428i
#> 4 12.81523 8.769051 0.06 0.06 12.81523+ 8.769051i
#> 5 12.23115 9.442454 0.08 0.08 12.23115+ 9.442454i
#> 6 11.68720 10.103197 0.10 0.10 11.68720+10.103197i
#> 7 11.14473 10.918745 0.12 0.12 11.14473+10.918745i
#> 8 10.61478 11.767438 0.14 0.14 10.61478+11.767438i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_10 Sim_10 TrajSim_10_10
#> 2 -0.5845274+0.6528443i Traj_10 Sim_10 TrajSim_10_10
#> 3 -0.6650780+0.6275834i Traj_10 Sim_10 TrajSim_10_10
#> 4 -0.6331642+0.6906231i Traj_10 Sim_10 TrajSim_10_10
#> 5 -0.5840836+0.6734035i Traj_10 Sim_10 TrajSim_10_10
#> 6 -0.5439492+0.6607430i Traj_10 Sim_10 TrajSim_10_10
#> 7 -0.5424664+0.8155480i Traj_10 Sim_10 TrajSim_10_10
#> 8 -0.5299472+0.8486923i Traj_10 Sim_10 TrajSim_10_10
#>
#> [[10]][[11]]
#> x y time displacementTime polar
#> 1 12.00600 7.316000 0.00 0.00 12.00600+ 7.316000i
#> 2 12.46898 8.187789 0.02 0.02 12.46898+ 8.187789i
#> 3 13.03315 9.153572 0.04 0.04 13.03315+ 9.153572i
#> 4 13.59474 10.090639 0.06 0.06 13.59474+10.090639i
#> 5 14.11447 11.016781 0.08 0.08 14.11447+11.016781i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_11 Sim_10 TrajSim_11_10
#> 2 0.4629776+0.8717895i Traj_11 Sim_10 TrajSim_11_10
#> 3 0.5641703+0.9657827i Traj_11 Sim_10 TrajSim_11_10
#> 4 0.5615914+0.9370666i Traj_11 Sim_10 TrajSim_11_10
#> 5 0.5197295+0.9261426i Traj_11 Sim_10 TrajSim_11_10
sim_directed_mount <- simulate_track(sbMountTom, nsim = 100, model = "Directed")
print(sim_directed_mount[1:10])#> [[1]]
#> [[1]][[1]]
#> x y time displacementTime polar
#> 1 36.88200 14.05600 0.00 0.00 36.88200+14.05600i
#> 2 36.35086 14.68156 0.02 0.02 36.35086+14.68156i
#> 3 35.69036 15.31312 0.04 0.04 35.69036+15.31312i
#> 4 35.08151 15.96721 0.06 0.06 35.08151+15.96721i
#> 5 34.50629 16.61834 0.08 0.08 34.50629+16.61834i
#> 6 33.87537 17.27341 0.10 0.10 33.87537+17.27341i
#> 7 33.24407 17.90479 0.12 0.12 33.24407+17.90479i
#> 8 32.60333 18.53624 0.14 0.14 32.60333+18.53624i
#> 9 32.00116 19.06803 0.16 0.16 32.00116+19.06803i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_1 Sim_1 TrajSim_1_1
#> 2 -0.5311423+0.6255562i Traj_1 Sim_1 TrajSim_1_1
#> 3 -0.6604980+0.6315633i Traj_1 Sim_1 TrajSim_1_1
#> 4 -0.6088508+0.6540876i Traj_1 Sim_1 TrajSim_1_1
#> 5 -0.5752147+0.6511306i Traj_1 Sim_1 TrajSim_1_1
#> 6 -0.6309248+0.6550693i Traj_1 Sim_1 TrajSim_1_1
#> 7 -0.6312946+0.6313797i Traj_1 Sim_1 TrajSim_1_1
#> 8 -0.6407468+0.6314499i Traj_1 Sim_1 TrajSim_1_1
#> 9 -0.6021662+0.5317929i Traj_1 Sim_1 TrajSim_1_1
#>
#> [[1]][[2]]
#> x y time displacementTime polar
#> 1 35.53200 13.51600 0.00 0.00 35.53200+13.51600i
#> 2 34.96558 14.21460 0.02 0.02 34.96558+14.21460i
#> 3 34.41207 14.99341 0.04 0.04 34.41207+14.99341i
#> 4 33.71222 15.76396 0.06 0.06 33.71222+15.76396i
#> 5 33.07700 16.57915 0.08 0.08 33.07700+16.57915i
#> 6 32.52100 17.23670 0.10 0.10 32.52100+17.23670i
#> 7 31.80774 17.93745 0.12 0.12 31.80774+17.93745i
#> 8 31.08549 18.62439 0.14 0.14 31.08549+18.62439i
#> 9 30.43664 19.25011 0.16 0.16 30.43664+19.25011i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_2 Sim_1 TrajSim_2_1
#> 2 -0.5664231+0.6986018i Traj_2 Sim_1 TrajSim_2_1
#> 3 -0.5535045+0.7788048i Traj_2 Sim_1 TrajSim_2_1
#> 4 -0.6998518+0.7705499i Traj_2 Sim_1 TrajSim_2_1
#> 5 -0.6352207+0.8151966i Traj_2 Sim_1 TrajSim_2_1
#> 6 -0.5559954+0.6575503i Traj_2 Sim_1 TrajSim_2_1
#> 7 -0.7132652+0.7007511i Traj_2 Sim_1 TrajSim_2_1
#> 8 -0.7222508+0.6869401i Traj_2 Sim_1 TrajSim_2_1
#> 9 -0.6488492+0.6257186i Traj_2 Sim_1 TrajSim_2_1
#>
#> [[1]][[3]]
#> x y time displacementTime polar
#> 1 34.54800 14.10000 0.00 0.00 34.54800+14.10000i
#> 2 33.59844 15.11395 0.02 0.02 33.59844+15.11395i
#> 3 32.73648 16.09824 0.04 0.04 32.73648+16.09824i
#> 4 31.98967 16.87394 0.06 0.06 31.98967+16.87394i
#> 5 31.27398 17.67208 0.08 0.08 31.27398+17.67208i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_3 Sim_1 TrajSim_3_1
#> 2 -0.9495637+1.0139509i Traj_3 Sim_1 TrajSim_3_1
#> 3 -0.8619561+0.9842890i Traj_3 Sim_1 TrajSim_3_1
#> 4 -0.7468066+0.7757026i Traj_3 Sim_1 TrajSim_3_1
#> 5 -0.7156937+0.7981402i Traj_3 Sim_1 TrajSim_3_1
#>
#> [[1]][[4]]
#> x y time displacementTime polar
#> 1 32.26000 14.51800 0.00 0.00 32.26000+14.51800i
#> 2 31.50830 15.23568 0.02 0.02 31.50830+15.23568i
#> 3 30.83483 16.17561 0.04 0.04 30.83483+16.17561i
#> 4 30.20735 16.92388 0.06 0.06 30.20735+16.92388i
#> 5 29.69604 17.75175 0.08 0.08 29.69604+17.75175i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_4 Sim_1 TrajSim_4_1
#> 2 -0.7517015+0.7176826i Traj_4 Sim_1 TrajSim_4_1
#> 3 -0.6734687+0.9399299i Traj_4 Sim_1 TrajSim_4_1
#> 4 -0.6274756+0.7482725i Traj_4 Sim_1 TrajSim_4_1
#> 5 -0.5113129+0.8278669i Traj_4 Sim_1 TrajSim_4_1
#>
#> [[1]][[5]]
#> x y time displacementTime polar
#> 1 28.29000 13.57800 0.00 0.00 28.29000+13.57800i
#> 2 27.69970 14.23018 0.02 0.02 27.69970+14.23018i
#> 3 27.22428 14.99944 0.04 0.04 27.22428+14.99944i
#> 4 26.71680 15.85385 0.06 0.06 26.71680+15.85385i
#> 5 26.40165 16.52556 0.08 0.08 26.40165+16.52556i
#> 6 25.78041 17.24407 0.10 0.10 25.78041+17.24407i
#> 7 25.38830 17.90210 0.12 0.12 25.38830+17.90210i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_5 Sim_1 TrajSim_5_1
#> 2 -0.5903018+0.6521848i Traj_5 Sim_1 TrajSim_5_1
#> 3 -0.4754214+0.7692524i Traj_5 Sim_1 TrajSim_5_1
#> 4 -0.5074811+0.8544091i Traj_5 Sim_1 TrajSim_5_1
#> 5 -0.3151445+0.6717124i Traj_5 Sim_1 TrajSim_5_1
#> 6 -0.6212388+0.7185125i Traj_5 Sim_1 TrajSim_5_1
#> 7 -0.3921078+0.6580273i Traj_5 Sim_1 TrajSim_5_1
#>
#> [[1]][[6]]
#> x y time displacementTime polar
#> 1 26.19800 13.69800 0.00 0.00 26.19800+13.69800i
#> 2 25.62405 14.54054 0.02 0.02 25.62405+14.54054i
#> 3 25.06322 15.47651 0.04 0.04 25.06322+15.47651i
#> 4 24.59030 16.44205 0.06 0.06 24.59030+16.44205i
#> 5 24.05927 17.32505 0.08 0.08 24.05927+17.32505i
#> 6 23.58379 18.44281 0.10 0.10 23.58379+18.44281i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_6 Sim_1 TrajSim_6_1
#> 2 -0.5739475+0.8425365i Traj_6 Sim_1 TrajSim_6_1
#> 3 -0.5608350+0.9359749i Traj_6 Sim_1 TrajSim_6_1
#> 4 -0.4729225+0.9655387i Traj_6 Sim_1 TrajSim_6_1
#> 5 -0.5310208+0.8829952i Traj_6 Sim_1 TrajSim_6_1
#> 6 -0.4754866+1.1177646i Traj_6 Sim_1 TrajSim_6_1
#>
#> [[1]][[7]]
#> x y time displacementTime polar
#> 1 26.47200 15.49600 0.00 0.00 26.47200+15.49600i
#> 2 27.52360 15.00106 0.02 0.02 27.52360+15.00106i
#> 3 28.58002 14.49177 0.04 0.04 28.58002+14.49177i
#> 4 29.57615 14.01123 0.06 0.06 29.57615+14.01123i
#> 5 30.72801 13.58350 0.08 0.08 30.72801+13.58350i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_7 Sim_1 TrajSim_7_1
#> 2 1.0516017-0.4949432i Traj_7 Sim_1 TrajSim_7_1
#> 3 1.0564147-0.5092906i Traj_7 Sim_1 TrajSim_7_1
#> 4 0.9961299-0.4805324i Traj_7 Sim_1 TrajSim_7_1
#> 5 1.1518619-0.4277318i Traj_7 Sim_1 TrajSim_7_1
#>
#> [[1]][[8]]
#> x y time displacementTime polar
#> 1 13.21800 8.752000 0.00 0.00 13.21800+8.752000i
#> 2 13.01953 8.431148 0.02 0.02 13.01953+8.431148i
#> 3 12.83132 8.097226 0.04 0.04 12.83132+8.097226i
#> 4 12.61696 7.782207 0.06 0.06 12.61696+7.782207i
#> 5 12.30530 7.452400 0.08 0.08 12.30530+7.452400i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_8 Sim_1 TrajSim_8_1
#> 2 -0.1984747-0.3208521i Traj_8 Sim_1 TrajSim_8_1
#> 3 -0.1882082-0.3339218i Traj_8 Sim_1 TrajSim_8_1
#> 4 -0.2143536-0.3150194i Traj_8 Sim_1 TrajSim_8_1
#> 5 -0.3116670-0.3298066i Traj_8 Sim_1 TrajSim_8_1
#>
#> [[1]][[9]]
#> x y time displacementTime polar
#> 1 15.63800 8.164000 0.00 0.00 15.63800+ 8.164000i
#> 2 15.05450 8.879814 0.02 0.02 15.05450+ 8.879814i
#> 3 14.62935 9.876047 0.04 0.04 14.62935+ 9.876047i
#> 4 14.15303 10.802202 0.06 0.06 14.15303+10.802202i
#> 5 13.78578 11.734624 0.08 0.08 13.78578+11.734624i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_9 Sim_1 TrajSim_9_1
#> 2 -0.5834960+0.7158143i Traj_9 Sim_1 TrajSim_9_1
#> 3 -0.4251541+0.9962330i Traj_9 Sim_1 TrajSim_9_1
#> 4 -0.4763239+0.9261551i Traj_9 Sim_1 TrajSim_9_1
#> 5 -0.3672440+0.9324213i Traj_9 Sim_1 TrajSim_9_1
#>
#> [[1]][[10]]
#> x y time displacementTime polar
#> 1 14.69800 6.798000 0.00 0.00 14.69800+ 6.798000i
#> 2 14.13696 7.639590 0.02 0.02 14.13696+ 7.639590i
#> 3 13.57786 8.355654 0.04 0.04 13.57786+ 8.355654i
#> 4 13.09078 9.105102 0.06 0.06 13.09078+ 9.105102i
#> 5 12.56150 9.749233 0.08 0.08 12.56150+ 9.749233i
#> 6 11.88545 10.352782 0.10 0.10 11.88545+10.352782i
#> 7 11.21658 11.102671 0.12 0.12 11.21658+11.102671i
#> 8 10.57860 11.717147 0.14 0.14 10.57860+11.717147i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_10 Sim_1 TrajSim_10_1
#> 2 -0.5610411+0.8415899i Traj_10 Sim_1 TrajSim_10_1
#> 3 -0.5591010+0.7160639i Traj_10 Sim_1 TrajSim_10_1
#> 4 -0.4870740+0.7494482i Traj_10 Sim_1 TrajSim_10_1
#> 5 -0.5292839+0.6441307i Traj_10 Sim_1 TrajSim_10_1
#> 6 -0.6760518+0.6035489i Traj_10 Sim_1 TrajSim_10_1
#> 7 -0.6688635+0.7498898i Traj_10 Sim_1 TrajSim_10_1
#> 8 -0.6379865+0.6144754i Traj_10 Sim_1 TrajSim_10_1
#>
#> [[1]][[11]]
#> x y time displacementTime polar
#> 1 12.00600 7.316000 0.00 0.00 12.00600+ 7.316000i
#> 2 11.68181 8.066235 0.02 0.02 11.68181+ 8.066235i
#> 3 11.32946 9.071432 0.04 0.04 11.32946+ 9.071432i
#> 4 10.95603 10.157634 0.06 0.06 10.95603+10.157634i
#> 5 10.49438 11.092497 0.08 0.08 10.49438+11.092497i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_11 Sim_1 TrajSim_11_1
#> 2 -0.3241855+0.7502354i Traj_11 Sim_1 TrajSim_11_1
#> 3 -0.3523569+1.0051968i Traj_11 Sim_1 TrajSim_11_1
#> 4 -0.3734282+1.0862014i Traj_11 Sim_1 TrajSim_11_1
#> 5 -0.4616519+0.9348632i Traj_11 Sim_1 TrajSim_11_1
#>
#>
#> [[2]]
#> [[2]][[1]]
#> x y time displacementTime polar
#> 1 36.88200 14.05600 0.00 0.00 36.88200+14.05600i
#> 2 36.24861 14.64823 0.02 0.02 36.24861+14.64823i
#> 3 35.61535 15.22132 0.04 0.04 35.61535+15.22132i
#> 4 35.00475 15.93942 0.06 0.06 35.00475+15.93942i
#> 5 34.41452 16.55241 0.08 0.08 34.41452+16.55241i
#> 6 33.80399 17.16300 0.10 0.10 33.80399+17.16300i
#> 7 33.19903 17.74525 0.12 0.12 33.19903+17.74525i
#> 8 32.43956 18.30022 0.14 0.14 32.43956+18.30022i
#> 9 31.82696 18.95666 0.16 0.16 31.82696+18.95666i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_1 Sim_2 TrajSim_1_2
#> 2 -0.6333903+0.5922318i Traj_1 Sim_2 TrajSim_1_2
#> 3 -0.6332562+0.5730870i Traj_1 Sim_2 TrajSim_1_2
#> 4 -0.6106065+0.7180993i Traj_1 Sim_2 TrajSim_1_2
#> 5 -0.5902266+0.6129933i Traj_1 Sim_2 TrajSim_1_2
#> 6 -0.6105321+0.6105892i Traj_1 Sim_2 TrajSim_1_2
#> 7 -0.6049620+0.5822542i Traj_1 Sim_2 TrajSim_1_2
#> 8 -0.7594696+0.5549697i Traj_1 Sim_2 TrajSim_1_2
#> 9 -0.6125939+0.6564366i Traj_1 Sim_2 TrajSim_1_2
#>
#> [[2]][[2]]
#> x y time displacementTime polar
#> 1 35.53200 13.51600 0.00 0.00 35.53200+13.51600i
#> 2 34.87769 14.41353 0.02 0.02 34.87769+14.41353i
#> 3 34.27214 15.24490 0.04 0.04 34.27214+15.24490i
#> 4 33.63856 15.89042 0.06 0.06 33.63856+15.89042i
#> 5 32.93691 16.69760 0.08 0.08 32.93691+16.69760i
#> 6 32.36746 17.48845 0.10 0.10 32.36746+17.48845i
#> 7 31.79830 18.26868 0.12 0.12 31.79830+18.26868i
#> 8 31.28253 18.97855 0.14 0.14 31.28253+18.97855i
#> 9 30.70475 19.75625 0.16 0.16 30.70475+19.75625i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_2 Sim_2 TrajSim_2_2
#> 2 -0.6543078+0.8975346i Traj_2 Sim_2 TrajSim_2_2
#> 3 -0.6055505+0.8313618i Traj_2 Sim_2 TrajSim_2_2
#> 4 -0.6335827+0.6455227i Traj_2 Sim_2 TrajSim_2_2
#> 5 -0.7016494+0.8071768i Traj_2 Sim_2 TrajSim_2_2
#> 6 -0.5694516+0.7908576i Traj_2 Sim_2 TrajSim_2_2
#> 7 -0.5691566+0.7802304i Traj_2 Sim_2 TrajSim_2_2
#> 8 -0.5157740+0.7098667i Traj_2 Sim_2 TrajSim_2_2
#> 9 -0.5777784+0.7777016i Traj_2 Sim_2 TrajSim_2_2
#>
#> [[2]][[3]]
#> x y time displacementTime polar
#> 1 34.54800 14.10000 0.00 0.00 34.54800+14.10000i
#> 2 33.85991 14.78351 0.02 0.02 33.85991+14.78351i
#> 3 33.00609 15.79061 0.04 0.04 33.00609+15.79061i
#> 4 32.25801 16.61245 0.06 0.06 32.25801+16.61245i
#> 5 31.59186 17.36516 0.08 0.08 31.59186+17.36516i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_3 Sim_2 TrajSim_3_2
#> 2 -0.6880856+0.6835103i Traj_3 Sim_2 TrajSim_3_2
#> 3 -0.8538218+1.0071016i Traj_3 Sim_2 TrajSim_3_2
#> 4 -0.7480826+0.8218393i Traj_3 Sim_2 TrajSim_3_2
#> 5 -0.6661530+0.7527108i Traj_3 Sim_2 TrajSim_3_2
#>
#> [[2]][[4]]
#> x y time displacementTime polar
#> 1 32.26000 14.51800 0.00 0.00 32.26000+14.51800i
#> 2 31.81084 15.34652 0.02 0.02 31.81084+15.34652i
#> 3 31.13848 16.27213 0.04 0.04 31.13848+16.27213i
#> 4 30.56744 17.11398 0.06 0.06 30.56744+17.11398i
#> 5 29.96759 17.98601 0.08 0.08 29.96759+17.98601i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_4 Sim_2 TrajSim_4_2
#> 2 -0.4491638+0.8285190i Traj_4 Sim_2 TrajSim_4_2
#> 3 -0.6723515+0.9256129i Traj_4 Sim_2 TrajSim_4_2
#> 4 -0.5710496+0.8418446i Traj_4 Sim_2 TrajSim_4_2
#> 5 -0.5998448+0.8720358i Traj_4 Sim_2 TrajSim_4_2
#>
#> [[2]][[5]]
#> x y time displacementTime polar
#> 1 28.29000 13.57800 0.00 0.00 28.29000+13.57800i
#> 2 27.81763 14.38661 0.02 0.02 27.81763+14.38661i
#> 3 27.35651 15.05846 0.04 0.04 27.35651+15.05846i
#> 4 26.87810 15.59121 0.06 0.06 26.87810+15.59121i
#> 5 26.51177 16.20312 0.08 0.08 26.51177+16.20312i
#> 6 26.11463 16.82642 0.10 0.10 26.11463+16.82642i
#> 7 25.97061 17.58796 0.12 0.12 25.97061+17.58796i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_5 Sim_2 TrajSim_5_2
#> 2 -0.4723670+0.8086065i Traj_5 Sim_2 TrajSim_5_2
#> 3 -0.4611216+0.6718516i Traj_5 Sim_2 TrajSim_5_2
#> 4 -0.4784130+0.5327527i Traj_5 Sim_2 TrajSim_5_2
#> 5 -0.3663259+0.6119130i Traj_5 Sim_2 TrajSim_5_2
#> 6 -0.3971463+0.6232918i Traj_5 Sim_2 TrajSim_5_2
#> 7 -0.1440133+0.7615400i Traj_5 Sim_2 TrajSim_5_2
#>
#> [[2]][[6]]
#> x y time displacementTime polar
#> 1 26.19800 13.69800 0.00 0.00 26.19800+13.69800i
#> 2 25.60325 14.62881 0.02 0.02 25.60325+14.62881i
#> 3 25.01321 15.50051 0.04 0.04 25.01321+15.50051i
#> 4 24.50399 16.42676 0.06 0.06 24.50399+16.42676i
#> 5 24.03406 17.28183 0.08 0.08 24.03406+17.28183i
#> 6 23.48890 18.32011 0.10 0.10 23.48890+18.32011i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_6 Sim_2 TrajSim_6_2
#> 2 -0.5947516+0.9308105i Traj_6 Sim_2 TrajSim_6_2
#> 3 -0.5900407+0.8716983i Traj_6 Sim_2 TrajSim_6_2
#> 4 -0.5092212+0.9262534i Traj_6 Sim_2 TrajSim_6_2
#> 5 -0.4699255+0.8550644i Traj_6 Sim_2 TrajSim_6_2
#> 6 -0.5451652+1.0382813i Traj_6 Sim_2 TrajSim_6_2
#>
#> [[2]][[7]]
#> x y time displacementTime polar
#> 1 26.47200 15.49600 0.00 0.00 26.47200+15.49600i
#> 2 27.42991 15.01735 0.02 0.02 27.42991+15.01735i
#> 3 28.33459 14.59219 0.04 0.04 28.33459+14.59219i
#> 4 29.49640 14.15867 0.06 0.06 29.49640+14.15867i
#> 5 30.59554 13.62583 0.08 0.08 30.59554+13.62583i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_7 Sim_2 TrajSim_7_2
#> 2 0.9579068-0.4786474i Traj_7 Sim_2 TrajSim_7_2
#> 3 0.9046798-0.4251604i Traj_7 Sim_2 TrajSim_7_2
#> 4 1.1618155-0.4335187i Traj_7 Sim_2 TrajSim_7_2
#> 5 1.0991405-0.5328392i Traj_7 Sim_2 TrajSim_7_2
#>
#> [[2]][[8]]
#> x y time displacementTime polar
#> 1 13.21800 8.752000 0.00 0.00 13.21800+8.752000i
#> 2 13.05593 8.364043 0.02 0.02 13.05593+8.364043i
#> 3 12.94156 8.021772 0.04 0.04 12.94156+8.021772i
#> 4 12.67280 7.734503 0.06 0.06 12.67280+7.734503i
#> 5 12.50356 7.362409 0.08 0.08 12.50356+7.362409i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_8 Sim_2 TrajSim_8_2
#> 2 -0.1620725-0.3879571i Traj_8 Sim_2 TrajSim_8_2
#> 3 -0.1143633-0.3422712i Traj_8 Sim_2 TrajSim_8_2
#> 4 -0.2687617-0.2872688i Traj_8 Sim_2 TrajSim_8_2
#> 5 -0.1692382-0.3720938i Traj_8 Sim_2 TrajSim_8_2
#>
#> [[2]][[9]]
#> x y time displacementTime polar
#> 1 15.63800 8.164000 0.00 0.00 15.63800+ 8.164000i
#> 2 15.18832 9.187561 0.02 0.02 15.18832+ 9.187561i
#> 3 14.66999 10.024323 0.04 0.04 14.66999+10.024323i
#> 4 14.22854 10.880939 0.06 0.06 14.22854+10.880939i
#> 5 13.75749 11.747573 0.08 0.08 13.75749+11.747573i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_9 Sim_2 TrajSim_9_2
#> 2 -0.4496793+1.0235611i Traj_9 Sim_2 TrajSim_9_2
#> 3 -0.5183350+0.8367617i Traj_9 Sim_2 TrajSim_9_2
#> 4 -0.4414438+0.8566162i Traj_9 Sim_2 TrajSim_9_2
#> 5 -0.4710517+0.8666337i Traj_9 Sim_2 TrajSim_9_2
#>
#> [[2]][[10]]
#> x y time displacementTime polar
#> 1 14.69800 6.798000 0.00 0.00 14.69800+ 6.798000i
#> 2 14.08137 7.426522 0.02 0.02 14.08137+ 7.426522i
#> 3 13.52744 8.212438 0.04 0.04 13.52744+ 8.212438i
#> 4 12.84327 8.900676 0.06 0.06 12.84327+ 8.900676i
#> 5 12.27658 9.682573 0.08 0.08 12.27658+ 9.682573i
#> 6 11.70699 10.424716 0.10 0.10 11.70699+10.424716i
#> 7 11.31013 11.194262 0.12 0.12 11.31013+11.194262i
#> 8 10.66569 11.965776 0.14 0.14 10.66569+11.965776i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_10 Sim_2 TrajSim_10_2
#> 2 -0.6166275+0.6285215i Traj_10 Sim_2 TrajSim_10_2
#> 3 -0.5539313+0.7859164i Traj_10 Sim_2 TrajSim_10_2
#> 4 -0.6841759+0.6882378i Traj_10 Sim_2 TrajSim_10_2
#> 5 -0.5666802+0.7818968i Traj_10 Sim_2 TrajSim_10_2
#> 6 -0.5695966+0.7421432i Traj_10 Sim_2 TrajSim_10_2
#> 7 -0.3968580+0.7695466i Traj_10 Sim_2 TrajSim_10_2
#> 8 -0.6444442+0.7715134i Traj_10 Sim_2 TrajSim_10_2
#>
#> [[2]][[11]]
#> x y time displacementTime polar
#> 1 12.00600 7.316000 0.00 0.00 12.00600+ 7.316000i
#> 2 11.60057 8.300159 0.02 0.02 11.60057+ 8.300159i
#> 3 11.19377 9.356871 0.04 0.04 11.19377+ 9.356871i
#> 4 10.91361 10.404312 0.06 0.06 10.91361+10.404312i
#> 5 10.51223 11.359930 0.08 0.08 10.51223+11.359930i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_11 Sim_2 TrajSim_11_2
#> 2 -0.4054284+0.9841593i Traj_11 Sim_2 TrajSim_11_2
#> 3 -0.4068002+1.0567116i Traj_11 Sim_2 TrajSim_11_2
#> 4 -0.2801564+1.0474409i Traj_11 Sim_2 TrajSim_11_2
#> 5 -0.4013804+0.9556187i Traj_11 Sim_2 TrajSim_11_2
#>
#>
#> [[3]]
#> [[3]][[1]]
#> x y time displacementTime polar
#> 1 36.88200 14.05600 0.00 0.00 36.88200+14.05600i
#> 2 36.18236 14.64727 0.02 0.02 36.18236+14.64727i
#> 3 35.52687 15.27251 0.04 0.04 35.52687+15.27251i
#> 4 34.94575 15.86193 0.06 0.06 34.94575+15.86193i
#> 5 34.27444 16.43341 0.08 0.08 34.27444+16.43341i
#> 6 33.66423 17.02306 0.10 0.10 33.66423+17.02306i
#> 7 33.09676 17.74553 0.12 0.12 33.09676+17.74553i
#> 8 32.45495 18.36273 0.14 0.14 32.45495+18.36273i
#> 9 31.79551 18.99080 0.16 0.16 31.79551+18.99080i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_1 Sim_3 TrajSim_1_3
#> 2 -0.6996385+0.5912672i Traj_1 Sim_3 TrajSim_1_3
#> 3 -0.6554957+0.6252425i Traj_1 Sim_3 TrajSim_1_3
#> 4 -0.5811171+0.5894243i Traj_1 Sim_3 TrajSim_1_3
#> 5 -0.6713082+0.5714724i Traj_1 Sim_3 TrajSim_1_3
#> 6 -0.6102098+0.5896494i Traj_1 Sim_3 TrajSim_1_3
#> 7 -0.5674735+0.7224706i Traj_1 Sim_3 TrajSim_1_3
#> 8 -0.6418053+0.6172067i Traj_1 Sim_3 TrajSim_1_3
#> 9 -0.6594394+0.6280621i Traj_1 Sim_3 TrajSim_1_3
#>
#> [[3]][[2]]
#> x y time displacementTime polar
#> 1 35.53200 13.51600 0.00 0.00 35.53200+13.51600i
#> 2 34.87843 14.14048 0.02 0.02 34.87843+14.14048i
#> 3 34.37084 14.94471 0.04 0.04 34.37084+14.94471i
#> 4 33.74124 15.55897 0.06 0.06 33.74124+15.55897i
#> 5 33.13655 16.30777 0.08 0.08 33.13655+16.30777i
#> 6 32.56055 17.10039 0.10 0.10 32.56055+17.10039i
#> 7 31.96014 17.74582 0.12 0.12 31.96014+17.74582i
#> 8 31.33358 18.44383 0.14 0.14 31.33358+18.44383i
#> 9 30.88540 19.25463 0.16 0.16 30.88540+19.25463i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_2 Sim_3 TrajSim_2_3
#> 2 -0.6535692+0.6244763i Traj_2 Sim_3 TrajSim_2_3
#> 3 -0.5075861+0.8042352i Traj_2 Sim_3 TrajSim_2_3
#> 4 -0.6296053+0.6142551i Traj_2 Sim_3 TrajSim_2_3
#> 5 -0.6046922+0.7488009i Traj_2 Sim_3 TrajSim_2_3
#> 6 -0.5759926+0.7926253i Traj_2 Sim_3 TrajSim_2_3
#> 7 -0.6004122+0.6454297i Traj_2 Sim_3 TrajSim_2_3
#> 8 -0.6265594+0.6980040i Traj_2 Sim_3 TrajSim_2_3
#> 9 -0.4481836+0.8108022i Traj_2 Sim_3 TrajSim_2_3
#>
#> [[3]][[3]]
#> x y time displacementTime polar
#> 1 34.54800 14.10000 0.00 0.00 34.54800+14.10000i
#> 2 33.62866 15.06518 0.02 0.02 33.62866+15.06518i
#> 3 32.87388 15.95469 0.04 0.04 32.87388+15.95469i
#> 4 32.12194 16.72450 0.06 0.06 32.12194+16.72450i
#> 5 31.23531 17.66244 0.08 0.08 31.23531+17.66244i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_3 Sim_3 TrajSim_3_3
#> 2 -0.9193353+0.9651776i Traj_3 Sim_3 TrajSim_3_3
#> 3 -0.7547838+0.8895104i Traj_3 Sim_3 TrajSim_3_3
#> 4 -0.7519435+0.7698109i Traj_3 Sim_3 TrajSim_3_3
#> 5 -0.8866268+0.9379459i Traj_3 Sim_3 TrajSim_3_3
#>
#> [[3]][[4]]
#> x y time displacementTime polar
#> 1 32.26000 14.51800 0.00 0.00 32.26000+14.51800i
#> 2 31.66525 15.30643 0.02 0.02 31.66525+15.30643i
#> 3 31.03768 16.18212 0.04 0.04 31.03768+16.18212i
#> 4 30.37878 17.08998 0.06 0.06 30.37878+17.08998i
#> 5 29.77412 17.96628 0.08 0.08 29.77412+17.96628i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_4 Sim_3 TrajSim_4_3
#> 2 -0.5947451+0.7884297i Traj_4 Sim_3 TrajSim_4_3
#> 3 -0.6275726+0.8756947i Traj_4 Sim_3 TrajSim_4_3
#> 4 -0.6589050+0.9078602i Traj_4 Sim_3 TrajSim_4_3
#> 5 -0.6046609+0.8763003i Traj_4 Sim_3 TrajSim_4_3
#>
#> [[3]][[5]]
#> x y time displacementTime polar
#> 1 28.29000 13.57800 0.00 0.00 28.29000+13.57800i
#> 2 27.98560 14.29665 0.02 0.02 27.98560+14.29665i
#> 3 27.72051 14.98556 0.04 0.04 27.72051+14.98556i
#> 4 27.30868 15.75631 0.06 0.06 27.30868+15.75631i
#> 5 26.82173 16.46570 0.08 0.08 26.82173+16.46570i
#> 6 26.39136 17.01916 0.10 0.10 26.39136+17.01916i
#> 7 25.89306 17.92044 0.12 0.12 25.89306+17.92044i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_5 Sim_3 TrajSim_5_3
#> 2 -0.3044049+0.7186529i Traj_5 Sim_3 TrajSim_5_3
#> 3 -0.2650835+0.6889089i Traj_5 Sim_3 TrajSim_5_3
#> 4 -0.4118341+0.7707466i Traj_5 Sim_3 TrajSim_5_3
#> 5 -0.4869436+0.7093894i Traj_5 Sim_3 TrajSim_5_3
#> 6 -0.4303788+0.5534626i Traj_5 Sim_3 TrajSim_5_3
#> 7 -0.4982942+0.9012777i Traj_5 Sim_3 TrajSim_5_3
#>
#> [[3]][[6]]
#> x y time displacementTime polar
#> 1 26.19800 13.69800 0.00 0.00 26.19800+13.69800i
#> 2 25.53172 14.67512 0.02 0.02 25.53172+14.67512i
#> 3 24.85384 15.68680 0.04 0.04 24.85384+15.68680i
#> 4 24.28772 16.61256 0.06 0.06 24.28772+16.61256i
#> 5 23.70117 17.60869 0.08 0.08 23.70117+17.60869i
#> 6 23.07935 18.46015 0.10 0.10 23.07935+18.46015i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_6 Sim_3 TrajSim_6_3
#> 2 -0.6662809+0.9771211i Traj_6 Sim_3 TrajSim_6_3
#> 3 -0.6778829+1.0116824i Traj_6 Sim_3 TrajSim_6_3
#> 4 -0.5661211+0.9257546i Traj_6 Sim_3 TrajSim_6_3
#> 5 -0.5865465+0.9961330i Traj_6 Sim_3 TrajSim_6_3
#> 6 -0.6218146+0.8514621i Traj_6 Sim_3 TrajSim_6_3
#>
#> [[3]][[7]]
#> x y time displacementTime polar
#> 1 26.47200 15.49600 0.00 0.00 26.47200+15.49600i
#> 2 27.61367 14.93954 0.02 0.02 27.61367+14.93954i
#> 3 28.65375 14.39540 0.04 0.04 28.65375+14.39540i
#> 4 29.81358 13.92057 0.06 0.06 29.81358+13.92057i
#> 5 30.80803 13.55660 0.08 0.08 30.80803+13.55660i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_7 Sim_3 TrajSim_7_3
#> 2 1.1416746-0.5564582i Traj_7 Sim_3 TrajSim_7_3
#> 3 1.0400767-0.5441393i Traj_7 Sim_3 TrajSim_7_3
#> 4 1.1598314-0.4748373i Traj_7 Sim_3 TrajSim_7_3
#> 5 0.9944482-0.3639680i Traj_7 Sim_3 TrajSim_7_3
#>
#> [[3]][[8]]
#> x y time displacementTime polar
#> 1 13.21800 8.752000 0.00 0.00 13.21800+8.752000i
#> 2 12.97987 8.429026 0.02 0.02 12.97987+8.429026i
#> 3 12.88885 7.973461 0.04 0.04 12.88885+7.973461i
#> 4 12.67894 7.586486 0.06 0.06 12.67894+7.586486i
#> 5 12.41274 7.296502 0.08 0.08 12.41274+7.296502i
#> displacement Trajectory Simulation TrajSim
#> 1 0.00000000+0.0000000i Traj_8 Sim_3 TrajSim_8_3
#> 2 -0.23813170-0.3229743i Traj_8 Sim_3 TrajSim_8_3
#> 3 -0.09101966-0.4555642i Traj_8 Sim_3 TrajSim_8_3
#> 4 -0.20990913-0.3869759i Traj_8 Sim_3 TrajSim_8_3
#> 5 -0.26619953-0.2899834i Traj_8 Sim_3 TrajSim_8_3
#>
#> [[3]][[9]]
#> x y time displacementTime polar
#> 1 15.63800 8.164000 0.00 0.00 15.63800+ 8.164000i
#> 2 15.21713 9.112660 0.02 0.02 15.21713+ 9.112660i
#> 3 14.65081 9.958626 0.04 0.04 14.65081+ 9.958626i
#> 4 14.28683 10.933085 0.06 0.06 14.28683+10.933085i
#> 5 13.87424 11.809764 0.08 0.08 13.87424+11.809764i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_9 Sim_3 TrajSim_9_3
#> 2 -0.4208738+0.9486602i Traj_9 Sim_3 TrajSim_9_3
#> 3 -0.5663177+0.8459660i Traj_9 Sim_3 TrajSim_9_3
#> 4 -0.3639792+0.9744589i Traj_9 Sim_3 TrajSim_9_3
#> 5 -0.4125931+0.8766794i Traj_9 Sim_3 TrajSim_9_3
#>
#> [[3]][[10]]
#> x y time displacementTime polar
#> 1 14.69800 6.798000 0.00 0.00 14.69800+ 6.798000i
#> 2 14.12760 7.508060 0.02 0.02 14.12760+ 7.508060i
#> 3 13.57375 8.271910 0.04 0.04 13.57375+ 8.271910i
#> 4 13.18558 9.032490 0.06 0.06 13.18558+ 9.032490i
#> 5 12.44212 9.677325 0.08 0.08 12.44212+ 9.677325i
#> 6 11.96278 10.357659 0.10 0.10 11.96278+10.357659i
#> 7 11.46259 11.174483 0.12 0.12 11.46259+11.174483i
#> 8 10.77192 11.897615 0.14 0.14 10.77192+11.897615i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_10 Sim_3 TrajSim_10_3
#> 2 -0.5703991+0.7100599i Traj_10 Sim_3 TrajSim_10_3
#> 3 -0.5538548+0.7638497i Traj_10 Sim_3 TrajSim_10_3
#> 4 -0.3881653+0.7605802i Traj_10 Sim_3 TrajSim_10_3
#> 5 -0.7434558+0.6448354i Traj_10 Sim_3 TrajSim_10_3
#> 6 -0.4793497+0.6803339i Traj_10 Sim_3 TrajSim_10_3
#> 7 -0.5001815+0.8168243i Traj_10 Sim_3 TrajSim_10_3
#> 8 -0.6906776+0.7231312i Traj_10 Sim_3 TrajSim_10_3
#>
#> [[3]][[11]]
#> x y time displacementTime polar
#> 1 12.00600 7.316000 0.00 0.00 12.00600+ 7.316000i
#> 2 11.62767 8.263001 0.02 0.02 11.62767+ 8.263001i
#> 3 11.27515 9.322749 0.04 0.04 11.27515+ 9.322749i
#> 4 10.93681 10.276484 0.06 0.06 10.93681+10.276484i
#> 5 10.53245 11.377548 0.08 0.08 10.53245+11.377548i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_11 Sim_3 TrajSim_11_3
#> 2 -0.3783305+0.9470009i Traj_11 Sim_3 TrajSim_11_3
#> 3 -0.3525170+1.0597485i Traj_11 Sim_3 TrajSim_11_3
#> 4 -0.3383471+0.9537349i Traj_11 Sim_3 TrajSim_11_3
#> 5 -0.4043545+1.1010633i Traj_11 Sim_3 TrajSim_11_3
#>
#>
#> [[4]]
#> [[4]][[1]]
#> x y time displacementTime polar
#> 1 36.88200 14.05600 0.00 0.00 36.88200+14.05600i
#> 2 36.19564 14.65429 0.02 0.02 36.19564+14.65429i
#> 3 35.54513 15.22261 0.04 0.04 35.54513+15.22261i
#> 4 34.89390 15.85890 0.06 0.06 34.89390+15.85890i
#> 5 34.27946 16.34205 0.08 0.08 34.27946+16.34205i
#> 6 33.62465 16.99530 0.10 0.10 33.62465+16.99530i
#> 7 33.03851 17.59949 0.12 0.12 33.03851+17.59949i
#> 8 32.35398 18.16640 0.14 0.14 32.35398+18.16640i
#> 9 31.74929 18.63998 0.16 0.16 31.74929+18.63998i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_1 Sim_4 TrajSim_1_4
#> 2 -0.6863648+0.5982931i Traj_1 Sim_4 TrajSim_1_4
#> 3 -0.6505093+0.5683205i Traj_1 Sim_4 TrajSim_1_4
#> 4 -0.6512296+0.6362855i Traj_1 Sim_4 TrajSim_1_4
#> 5 -0.6144341+0.4831520i Traj_1 Sim_4 TrajSim_1_4
#> 6 -0.6548089+0.6532481i Traj_1 Sim_4 TrajSim_1_4
#> 7 -0.5861398+0.6041891i Traj_1 Sim_4 TrajSim_1_4
#> 8 -0.6845374+0.5669108i Traj_1 Sim_4 TrajSim_1_4
#> 9 -0.6046870+0.4735777i Traj_1 Sim_4 TrajSim_1_4
#>
#> [[4]][[2]]
#> x y time displacementTime polar
#> 1 35.53200 13.51600 0.00 0.00 35.53200+13.51600i
#> 2 35.10299 14.31063 0.02 0.02 35.10299+14.31063i
#> 3 34.54936 15.18122 0.04 0.04 34.54936+15.18122i
#> 4 34.01168 16.03371 0.06 0.06 34.01168+16.03371i
#> 5 33.44078 16.66133 0.08 0.08 33.44078+16.66133i
#> 6 32.82108 17.38854 0.10 0.10 32.82108+17.38854i
#> 7 32.11256 18.24117 0.12 0.12 32.11256+18.24117i
#> 8 31.54872 18.99807 0.14 0.14 31.54872+18.99807i
#> 9 31.07972 19.72442 0.16 0.16 31.07972+19.72442i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_2 Sim_4 TrajSim_2_4
#> 2 -0.4290080+0.7946280i Traj_2 Sim_4 TrajSim_2_4
#> 3 -0.5536315+0.8705926i Traj_2 Sim_4 TrajSim_2_4
#> 4 -0.5376795+0.8524938i Traj_2 Sim_4 TrajSim_2_4
#> 5 -0.5709044+0.6276148i Traj_2 Sim_4 TrajSim_2_4
#> 6 -0.6196967+0.7272076i Traj_2 Sim_4 TrajSim_2_4
#> 7 -0.7085195+0.8526318i Traj_2 Sim_4 TrajSim_2_4
#> 8 -0.5638429+0.7568967i Traj_2 Sim_4 TrajSim_2_4
#> 9 -0.4689974+0.7263573i Traj_2 Sim_4 TrajSim_2_4
#>
#> [[4]][[3]]
#> x y time displacementTime polar
#> 1 34.54800 14.10000 0.00 0.00 34.54800+14.10000i
#> 2 33.75636 15.00287 0.02 0.02 33.75636+15.00287i
#> 3 33.03185 15.76350 0.04 0.04 33.03185+15.76350i
#> 4 32.30396 16.52185 0.06 0.06 32.30396+16.52185i
#> 5 31.60414 17.31885 0.08 0.08 31.60414+17.31885i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_3 Sim_4 TrajSim_3_4
#> 2 -0.7916368+0.9028671i Traj_3 Sim_4 TrajSim_3_4
#> 3 -0.7245089+0.7606321i Traj_3 Sim_4 TrajSim_3_4
#> 4 -0.7278903+0.7583540i Traj_3 Sim_4 TrajSim_3_4
#> 5 -0.6998244+0.7969952i Traj_3 Sim_4 TrajSim_3_4
#>
#> [[4]][[4]]
#> x y time displacementTime polar
#> 1 32.26000 14.51800 0.00 0.00 32.26000+14.51800i
#> 2 31.54336 15.36940 0.02 0.02 31.54336+15.36940i
#> 3 30.92055 16.22135 0.04 0.04 30.92055+16.22135i
#> 4 30.23640 17.04902 0.06 0.06 30.23640+17.04902i
#> 5 29.67429 17.89683 0.08 0.08 29.67429+17.89683i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_4 Sim_4 TrajSim_4_4
#> 2 -0.7166445+0.8513985i Traj_4 Sim_4 TrajSim_4_4
#> 3 -0.6228059+0.8519486i Traj_4 Sim_4 TrajSim_4_4
#> 4 -0.6841459+0.8276721i Traj_4 Sim_4 TrajSim_4_4
#> 5 -0.5621129+0.8478102i Traj_4 Sim_4 TrajSim_4_4
#>
#> [[4]][[5]]
#> x y time displacementTime polar
#> 1 28.29000 13.57800 0.00 0.00 28.29000+13.57800i
#> 2 27.76895 14.27666 0.02 0.02 27.76895+14.27666i
#> 3 27.20642 14.90312 0.04 0.04 27.20642+14.90312i
#> 4 26.63949 15.52450 0.06 0.06 26.63949+15.52450i
#> 5 26.08810 16.24483 0.08 0.08 26.08810+16.24483i
#> 6 25.83482 17.05966 0.10 0.10 25.83482+17.05966i
#> 7 25.33282 17.80283 0.12 0.12 25.33282+17.80283i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_5 Sim_4 TrajSim_5_4
#> 2 -0.5210494+0.6986561i Traj_5 Sim_4 TrajSim_5_4
#> 3 -0.5625257+0.6264665i Traj_5 Sim_4 TrajSim_5_4
#> 4 -0.5669398+0.6213736i Traj_5 Sim_4 TrajSim_5_4
#> 5 -0.5513837+0.7203329i Traj_5 Sim_4 TrajSim_5_4
#> 6 -0.2532855+0.8148336i Traj_5 Sim_4 TrajSim_5_4
#> 7 -0.5019924+0.7431672i Traj_5 Sim_4 TrajSim_5_4
#>
#> [[4]][[6]]
#> x y time displacementTime polar
#> 1 26.19800 13.69800 0.00 0.00 26.19800+13.69800i
#> 2 25.62950 14.66688 0.02 0.02 25.62950+14.66688i
#> 3 25.08295 15.58156 0.04 0.04 25.08295+15.58156i
#> 4 24.48168 16.54289 0.06 0.06 24.48168+16.54289i
#> 5 23.76063 17.44759 0.08 0.08 23.76063+17.44759i
#> 6 23.12611 18.42740 0.10 0.10 23.12611+18.42740i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_6 Sim_4 TrajSim_6_4
#> 2 -0.5684990+0.9688794i Traj_6 Sim_4 TrajSim_6_4
#> 3 -0.5465487+0.9146785i Traj_6 Sim_4 TrajSim_6_4
#> 4 -0.6012732+0.9613360i Traj_6 Sim_4 TrajSim_6_4
#> 5 -0.7210472+0.9046983i Traj_6 Sim_4 TrajSim_6_4
#> 6 -0.6345222+0.9798079i Traj_6 Sim_4 TrajSim_6_4
#>
#> [[4]][[7]]
#> x y time displacementTime polar
#> 1 26.47200 15.49600 0.00 0.00 26.47200+15.49600i
#> 2 27.51748 15.03061 0.02 0.02 27.51748+15.03061i
#> 3 28.61416 14.56892 0.04 0.04 28.61416+14.56892i
#> 4 29.70904 14.12146 0.06 0.06 29.70904+14.12146i
#> 5 30.82765 13.59815 0.08 0.08 30.82765+13.59815i
#> displacement Trajectory Simulation TrajSim
#> 1 0.000000+0.0000000i Traj_7 Sim_4 TrajSim_7_4
#> 2 1.045478-0.4653908i Traj_7 Sim_4 TrajSim_7_4
#> 3 1.096686-0.4616939i Traj_7 Sim_4 TrajSim_7_4
#> 4 1.094874-0.4474574i Traj_7 Sim_4 TrajSim_7_4
#> 5 1.118609-0.5233104i Traj_7 Sim_4 TrajSim_7_4
#>
#> [[4]][[8]]
#> x y time displacementTime polar
#> 1 13.21800 8.752000 0.00 0.00 13.21800+8.752000i
#> 2 12.83724 8.541028 0.02 0.02 12.83724+8.541028i
#> 3 12.56039 8.235235 0.04 0.04 12.56039+8.235235i
#> 4 12.32453 7.840580 0.06 0.06 12.32453+7.840580i
#> 5 12.11062 7.507642 0.08 0.08 12.11062+7.507642i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_8 Sim_4 TrajSim_8_4
#> 2 -0.3807614-0.2109725i Traj_8 Sim_4 TrajSim_8_4
#> 3 -0.2768437-0.3057925i Traj_8 Sim_4 TrajSim_8_4
#> 4 -0.2358639-0.3946548i Traj_8 Sim_4 TrajSim_8_4
#> 5 -0.2139142-0.3329380i Traj_8 Sim_4 TrajSim_8_4
#>
#> [[4]][[9]]
#> x y time displacementTime polar
#> 1 15.63800 8.164000 0.00 0.00 15.63800+ 8.164000i
#> 2 15.00767 9.091586 0.02 0.02 15.00767+ 9.091586i
#> 3 14.49697 9.932339 0.04 0.04 14.49697+ 9.932339i
#> 4 14.16841 10.838742 0.06 0.06 14.16841+10.838742i
#> 5 13.66303 11.753124 0.08 0.08 13.66303+11.753124i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_9 Sim_4 TrajSim_9_4
#> 2 -0.6303298+0.9275859i Traj_9 Sim_4 TrajSim_9_4
#> 3 -0.5106959+0.8407535i Traj_9 Sim_4 TrajSim_9_4
#> 4 -0.3285679+0.9064024i Traj_9 Sim_4 TrajSim_9_4
#> 5 -0.5053734+0.9143818i Traj_9 Sim_4 TrajSim_9_4
#>
#> [[4]][[10]]
#> x y time displacementTime polar
#> 1 14.69800 6.798000 0.00 0.00 14.69800+ 6.798000i
#> 2 14.16359 7.539877 0.02 0.02 14.16359+ 7.539877i
#> 3 13.59853 8.287853 0.04 0.04 13.59853+ 8.287853i
#> 4 13.01300 9.067979 0.06 0.06 13.01300+ 9.067979i
#> 5 12.68450 9.883318 0.08 0.08 12.68450+ 9.883318i
#> 6 12.07646 10.681503 0.10 0.10 12.07646+10.681503i
#> 7 11.69180 11.431208 0.12 0.12 11.69180+11.431208i
#> 8 11.09362 12.238543 0.14 0.14 11.09362+12.238543i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_10 Sim_4 TrajSim_10_4
#> 2 -0.5344071+0.7418769i Traj_10 Sim_4 TrajSim_10_4
#> 3 -0.5650673+0.7479762i Traj_10 Sim_4 TrajSim_10_4
#> 4 -0.5855302+0.7801259i Traj_10 Sim_4 TrajSim_10_4
#> 5 -0.3284986+0.8153388i Traj_10 Sim_4 TrajSim_10_4
#> 6 -0.6080365+0.7981855i Traj_10 Sim_4 TrajSim_10_4
#> 7 -0.3846599+0.7497045i Traj_10 Sim_4 TrajSim_10_4
#> 8 -0.5981807+0.8073347i Traj_10 Sim_4 TrajSim_10_4
#>
#> [[4]][[11]]
#> x y time displacementTime polar
#> 1 12.00600 7.316000 0.00 0.00 12.00600+ 7.316000i
#> 2 11.62001 8.255487 0.02 0.02 11.62001+ 8.255487i
#> 3 11.28149 9.282384 0.04 0.04 11.28149+ 9.282384i
#> 4 10.98821 10.225629 0.06 0.06 10.98821+10.225629i
#> 5 10.54005 11.387190 0.08 0.08 10.54005+11.387190i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_11 Sim_4 TrajSim_11_4
#> 2 -0.3859921+0.9394869i Traj_11 Sim_4 TrajSim_11_4
#> 3 -0.3385137+1.0268972i Traj_11 Sim_4 TrajSim_11_4
#> 4 -0.2932833+0.9432449i Traj_11 Sim_4 TrajSim_11_4
#> 5 -0.4481577+1.1615610i Traj_11 Sim_4 TrajSim_11_4
#>
#>
#> [[5]]
#> [[5]][[1]]
#> x y time displacementTime polar
#> 1 36.88200 14.05600 0.00 0.00 36.88200+14.05600i
#> 2 36.17180 14.66437 0.02 0.02 36.17180+14.66437i
#> 3 35.66618 15.26443 0.04 0.04 35.66618+15.26443i
#> 4 35.10818 15.75086 0.06 0.06 35.10818+15.75086i
#> 5 34.47605 16.31011 0.08 0.08 34.47605+16.31011i
#> 6 33.84395 16.97376 0.10 0.10 33.84395+16.97376i
#> 7 33.24008 17.56371 0.12 0.12 33.24008+17.56371i
#> 8 32.57714 18.18439 0.14 0.14 32.57714+18.18439i
#> 9 31.94948 18.83241 0.16 0.16 31.94948+18.83241i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_1 Sim_5 TrajSim_1_5
#> 2 -0.7101997+0.6083665i Traj_1 Sim_5 TrajSim_1_5
#> 3 -0.5056184+0.6000664i Traj_1 Sim_5 TrajSim_1_5
#> 4 -0.5580005+0.4864237i Traj_1 Sim_5 TrajSim_1_5
#> 5 -0.6321309+0.5592556i Traj_1 Sim_5 TrajSim_1_5
#> 6 -0.6321053+0.6636483i Traj_1 Sim_5 TrajSim_1_5
#> 7 -0.6038677+0.5899526i Traj_1 Sim_5 TrajSim_1_5
#> 8 -0.6629354+0.6206759i Traj_1 Sim_5 TrajSim_1_5
#> 9 -0.6276611+0.6480230i Traj_1 Sim_5 TrajSim_1_5
#>
#> [[5]][[2]]
#> x y time displacementTime polar
#> 1 35.53200 13.51600 0.00 0.00 35.53200+13.51600i
#> 2 34.75541 14.39211 0.02 0.02 34.75541+14.39211i
#> 3 34.25224 15.09577 0.04 0.04 34.25224+15.09577i
#> 4 33.72249 15.84871 0.06 0.06 33.72249+15.84871i
#> 5 33.13674 16.75715 0.08 0.08 33.13674+16.75715i
#> 6 32.58722 17.58409 0.10 0.10 32.58722+17.58409i
#> 7 31.99321 18.17063 0.12 0.12 31.99321+18.17063i
#> 8 31.37424 18.91736 0.14 0.14 31.37424+18.91736i
#> 9 30.81613 19.66847 0.16 0.16 30.81613+19.66847i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_2 Sim_5 TrajSim_2_5
#> 2 -0.7765882+0.8761052i Traj_2 Sim_5 TrajSim_2_5
#> 3 -0.5031698+0.7036629i Traj_2 Sim_5 TrajSim_2_5
#> 4 -0.5297555+0.7529435i Traj_2 Sim_5 TrajSim_2_5
#> 5 -0.5857484+0.9084427i Traj_2 Sim_5 TrajSim_2_5
#> 6 -0.5495191+0.8269328i Traj_2 Sim_5 TrajSim_2_5
#> 7 -0.5940103+0.5865398i Traj_2 Sim_5 TrajSim_2_5
#> 8 -0.6189728+0.7467326i Traj_2 Sim_5 TrajSim_2_5
#> 9 -0.5581020+0.7511120i Traj_2 Sim_5 TrajSim_2_5
#>
#> [[5]][[3]]
#> x y time displacementTime polar
#> 1 34.54800 14.10000 0.00 0.00 34.54800+14.10000i
#> 2 33.75384 14.97593 0.02 0.02 33.75384+14.97593i
#> 3 32.97670 15.89495 0.04 0.04 32.97670+15.89495i
#> 4 32.09940 16.91418 0.06 0.06 32.09940+16.91418i
#> 5 31.21691 17.79719 0.08 0.08 31.21691+17.79719i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_3 Sim_5 TrajSim_3_5
#> 2 -0.7941576+0.8759282i Traj_3 Sim_5 TrajSim_3_5
#> 3 -0.7771380+0.9190227i Traj_3 Sim_5 TrajSim_3_5
#> 4 -0.8773068+1.0192271i Traj_3 Sim_5 TrajSim_3_5
#> 5 -0.8824864+0.8830148i Traj_3 Sim_5 TrajSim_3_5
#>
#> [[5]][[4]]
#> x y time displacementTime polar
#> 1 32.26000 14.51800 0.00 0.00 32.26000+14.51800i
#> 2 31.59991 15.31051 0.02 0.02 31.59991+15.31051i
#> 3 30.99482 16.11190 0.04 0.04 30.99482+16.11190i
#> 4 30.30328 17.09333 0.06 0.06 30.30328+17.09333i
#> 5 29.65818 17.94407 0.08 0.08 29.65818+17.94407i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_4 Sim_5 TrajSim_4_5
#> 2 -0.6600878+0.7925059i Traj_4 Sim_5 TrajSim_4_5
#> 3 -0.6050937+0.8013935i Traj_4 Sim_5 TrajSim_4_5
#> 4 -0.6915336+0.9814352i Traj_4 Sim_5 TrajSim_4_5
#> 5 -0.6451043+0.8507357i Traj_4 Sim_5 TrajSim_4_5
#>
#> [[5]][[5]]
#> x y time displacementTime polar
#> 1 28.29000 13.57800 0.00 0.00 28.29000+13.57800i
#> 2 27.91541 14.15298 0.02 0.02 27.91541+14.15298i
#> 3 27.61132 14.99445 0.04 0.04 27.61132+14.99445i
#> 4 27.25623 15.68781 0.06 0.06 27.25623+15.68781i
#> 5 26.83729 16.50147 0.08 0.08 26.83729+16.50147i
#> 6 26.50743 17.28108 0.10 0.10 26.50743+17.28108i
#> 7 26.08370 17.89891 0.12 0.12 26.08370+17.89891i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_5 Sim_5 TrajSim_5_5
#> 2 -0.3745901+0.5749759i Traj_5 Sim_5 TrajSim_5_5
#> 3 -0.3040902+0.8414746i Traj_5 Sim_5 TrajSim_5_5
#> 4 -0.3550873+0.6933575i Traj_5 Sim_5 TrajSim_5_5
#> 5 -0.4189430+0.8136664i Traj_5 Sim_5 TrajSim_5_5
#> 6 -0.3298609+0.7796065i Traj_5 Sim_5 TrajSim_5_5
#> 7 -0.4237281+0.6178269i Traj_5 Sim_5 TrajSim_5_5
#>
#> [[5]][[6]]
#> x y time displacementTime polar
#> 1 26.19800 13.69800 0.00 0.00 26.19800+13.69800i
#> 2 25.67078 14.61055 0.02 0.02 25.67078+14.61055i
#> 3 25.05844 15.46317 0.04 0.04 25.05844+15.46317i
#> 4 24.43311 16.41612 0.06 0.06 24.43311+16.41612i
#> 5 23.88390 17.51117 0.08 0.08 23.88390+17.51117i
#> 6 23.35391 18.50341 0.10 0.10 23.35391+18.50341i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_6 Sim_5 TrajSim_6_5
#> 2 -0.5272213+0.9125471i Traj_6 Sim_5 TrajSim_6_5
#> 3 -0.6123376+0.8526237i Traj_6 Sim_5 TrajSim_6_5
#> 4 -0.6253272+0.9529464i Traj_6 Sim_5 TrajSim_6_5
#> 5 -0.5492162+1.0950507i Traj_6 Sim_5 TrajSim_6_5
#> 6 -0.5299858+0.9922427i Traj_6 Sim_5 TrajSim_6_5
#>
#> [[5]][[7]]
#> x y time displacementTime polar
#> 1 26.47200 15.49600 0.00 0.00 26.47200+15.49600i
#> 2 27.61298 15.12740 0.02 0.02 27.61298+15.12740i
#> 3 28.66002 14.72264 0.04 0.04 28.66002+14.72264i
#> 4 30.15375 14.25359 0.06 0.06 30.15375+14.25359i
#> 5 31.18867 13.77562 0.08 0.08 31.18867+13.77562i
#> displacement Trajectory Simulation TrajSim
#> 1 0.000000+0.0000000i Traj_7 Sim_5 TrajSim_7_5
#> 2 1.140984-0.3686041i Traj_7 Sim_5 TrajSim_7_5
#> 3 1.047035-0.4047609i Traj_7 Sim_5 TrajSim_7_5
#> 4 1.493728-0.4690439i Traj_7 Sim_5 TrajSim_7_5
#> 5 1.034927-0.4779700i Traj_7 Sim_5 TrajSim_7_5
#>
#> [[5]][[8]]
#> x y time displacementTime polar
#> 1 13.21800 8.752000 0.00 0.00 13.21800+8.752000i
#> 2 12.94281 8.505773 0.02 0.02 12.94281+8.505773i
#> 3 12.64223 8.261557 0.04 0.04 12.64223+8.261557i
#> 4 12.39116 7.987149 0.06 0.06 12.39116+7.987149i
#> 5 12.12433 7.664388 0.08 0.08 12.12433+7.664388i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_8 Sim_5 TrajSim_8_5
#> 2 -0.2751915-0.2462271i Traj_8 Sim_5 TrajSim_8_5
#> 3 -0.3005753-0.2442160i Traj_8 Sim_5 TrajSim_8_5
#> 4 -0.2510720-0.2744080i Traj_8 Sim_5 TrajSim_8_5
#> 5 -0.2668340-0.3227609i Traj_8 Sim_5 TrajSim_8_5
#>
#> [[5]][[9]]
#> x y time displacementTime polar
#> 1 15.63800 8.164000 0.00 0.00 15.63800+ 8.164000i
#> 2 15.13587 9.114345 0.02 0.02 15.13587+ 9.114345i
#> 3 14.69762 9.939939 0.04 0.04 14.69762+ 9.939939i
#> 4 14.38488 10.882033 0.06 0.06 14.38488+10.882033i
#> 5 14.07862 11.853352 0.08 0.08 14.07862+11.853352i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_9 Sim_5 TrajSim_9_5
#> 2 -0.5021255+0.9503447i Traj_9 Sim_5 TrajSim_9_5
#> 3 -0.4382568+0.8255940i Traj_9 Sim_5 TrajSim_9_5
#> 4 -0.3127353+0.9420948i Traj_9 Sim_5 TrajSim_9_5
#> 5 -0.3062641+0.9713183i Traj_9 Sim_5 TrajSim_9_5
#>
#> [[5]][[10]]
#> x y time displacementTime polar
#> 1 14.69800 6.798000 0.00 0.00 14.69800+ 6.798000i
#> 2 14.24125 7.513531 0.02 0.02 14.24125+ 7.513531i
#> 3 13.73091 8.338688 0.04 0.04 13.73091+ 8.338688i
#> 4 13.17828 8.898515 0.06 0.06 13.17828+ 8.898515i
#> 5 12.76215 9.606247 0.08 0.08 12.76215+ 9.606247i
#> 6 12.28855 10.352800 0.10 0.10 12.28855+10.352800i
#> 7 11.89074 11.108261 0.12 0.12 11.89074+11.108261i
#> 8 11.38085 11.931627 0.14 0.14 11.38085+11.931627i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_10 Sim_5 TrajSim_10_5
#> 2 -0.4567535+0.7155310i Traj_10 Sim_5 TrajSim_10_5
#> 3 -0.5103355+0.8251566i Traj_10 Sim_5 TrajSim_10_5
#> 4 -0.5526354+0.5598278i Traj_10 Sim_5 TrajSim_10_5
#> 5 -0.4161224+0.7077321i Traj_10 Sim_5 TrajSim_10_5
#> 6 -0.4736066+0.7465526i Traj_10 Sim_5 TrajSim_10_5
#> 7 -0.3978113+0.7554609i Traj_10 Sim_5 TrajSim_10_5
#> 8 -0.5098879+0.8233663i Traj_10 Sim_5 TrajSim_10_5
#>
#> [[5]][[11]]
#> x y time displacementTime polar
#> 1 12.00600 7.316000 0.00 0.00 12.00600+ 7.316000i
#> 2 11.51055 8.321650 0.02 0.02 11.51055+ 8.321650i
#> 3 11.06989 9.307127 0.04 0.04 11.06989+ 9.307127i
#> 4 10.64838 10.422110 0.06 0.06 10.64838+10.422110i
#> 5 10.25413 11.382987 0.08 0.08 10.25413+11.382987i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_11 Sim_5 TrajSim_11_5
#> 2 -0.4954520+1.0056498i Traj_11 Sim_5 TrajSim_11_5
#> 3 -0.4406560+0.9854771i Traj_11 Sim_5 TrajSim_11_5
#> 4 -0.4215080+1.1149827i Traj_11 Sim_5 TrajSim_11_5
#> 5 -0.3942564+0.9608774i Traj_11 Sim_5 TrajSim_11_5
#>
#>
#> [[6]]
#> [[6]][[1]]
#> x y time displacementTime polar
#> 1 36.88200 14.05600 0.00 0.00 36.88200+14.05600i
#> 2 36.11819 14.70909 0.02 0.02 36.11819+14.70909i
#> 3 35.53928 15.23567 0.04 0.04 35.53928+15.23567i
#> 4 34.84667 15.89950 0.06 0.06 34.84667+15.89950i
#> 5 34.24697 16.48063 0.08 0.08 34.24697+16.48063i
#> 6 33.75542 17.13172 0.10 0.10 33.75542+17.13172i
#> 7 33.12832 17.77825 0.12 0.12 33.12832+17.77825i
#> 8 32.45986 18.29357 0.14 0.14 32.45986+18.29357i
#> 9 31.80579 18.92646 0.16 0.16 31.80579+18.92646i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_1 Sim_6 TrajSim_1_6
#> 2 -0.7638066+0.6530940i Traj_1 Sim_6 TrajSim_1_6
#> 3 -0.5789100+0.5265781i Traj_1 Sim_6 TrajSim_1_6
#> 4 -0.6926171+0.6638272i Traj_1 Sim_6 TrajSim_1_6
#> 5 -0.5996954+0.5811336i Traj_1 Sim_6 TrajSim_1_6
#> 6 -0.4915479+0.6510884i Traj_1 Sim_6 TrajSim_1_6
#> 7 -0.6271033+0.6465331i Traj_1 Sim_6 TrajSim_1_6
#> 8 -0.6684585+0.5153184i Traj_1 Sim_6 TrajSim_1_6
#> 9 -0.6540738+0.6328849i Traj_1 Sim_6 TrajSim_1_6
#>
#> [[6]][[2]]
#> x y time displacementTime polar
#> 1 35.53200 13.51600 0.00 0.00 35.53200+13.51600i
#> 2 34.95967 14.14521 0.02 0.02 34.95967+14.14521i
#> 3 34.23776 14.76198 0.04 0.04 34.23776+14.76198i
#> 4 33.62608 15.45339 0.06 0.06 33.62608+15.45339i
#> 5 32.91950 16.25588 0.08 0.08 32.91950+16.25588i
#> 6 32.26923 16.99895 0.10 0.10 32.26923+16.99895i
#> 7 31.74742 17.73222 0.12 0.12 31.74742+17.73222i
#> 8 31.12649 18.46306 0.14 0.14 31.12649+18.46306i
#> 9 30.54114 19.10133 0.16 0.16 30.54114+19.10133i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_2 Sim_6 TrajSim_2_6
#> 2 -0.5723293+0.6292083i Traj_2 Sim_6 TrajSim_2_6
#> 3 -0.7219157+0.6167765i Traj_2 Sim_6 TrajSim_2_6
#> 4 -0.6116783+0.6914081i Traj_2 Sim_6 TrajSim_2_6
#> 5 -0.7065812+0.8024830i Traj_2 Sim_6 TrajSim_2_6
#> 6 -0.6502694+0.7430715i Traj_2 Sim_6 TrajSim_2_6
#> 7 -0.5218066+0.7332718i Traj_2 Sim_6 TrajSim_2_6
#> 8 -0.6209251+0.7308364i Traj_2 Sim_6 TrajSim_2_6
#> 9 -0.5853553+0.6382718i Traj_2 Sim_6 TrajSim_2_6
#>
#> [[6]][[3]]
#> x y time displacementTime polar
#> 1 34.54800 14.10000 0.00 0.00 34.54800+14.10000i
#> 2 33.83205 14.81816 0.02 0.02 33.83205+14.81816i
#> 3 33.14565 15.57834 0.04 0.04 33.14565+15.57834i
#> 4 32.37702 16.37127 0.06 0.06 32.37702+16.37127i
#> 5 31.56645 17.28079 0.08 0.08 31.56645+17.28079i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_3 Sim_6 TrajSim_3_6
#> 2 -0.7159521+0.7181580i Traj_3 Sim_6 TrajSim_3_6
#> 3 -0.6863939+0.7601777i Traj_3 Sim_6 TrajSim_3_6
#> 4 -0.7686377+0.7929350i Traj_3 Sim_6 TrajSim_3_6
#> 5 -0.8105637+0.9095210i Traj_3 Sim_6 TrajSim_3_6
#>
#> [[6]][[4]]
#> x y time displacementTime polar
#> 1 32.26000 14.51800 0.00 0.00 32.26000+14.51800i
#> 2 31.54921 15.35022 0.02 0.02 31.54921+15.35022i
#> 3 30.88574 16.05872 0.04 0.04 30.88574+16.05872i
#> 4 30.24491 17.01621 0.06 0.06 30.24491+17.01621i
#> 5 29.58190 17.80496 0.08 0.08 29.58190+17.80496i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_4 Sim_6 TrajSim_4_6
#> 2 -0.7107858+0.8322210i Traj_4 Sim_6 TrajSim_4_6
#> 3 -0.6634792+0.7084970i Traj_4 Sim_6 TrajSim_4_6
#> 4 -0.6408252+0.9574953i Traj_4 Sim_6 TrajSim_4_6
#> 5 -0.6630089+0.7887478i Traj_4 Sim_6 TrajSim_4_6
#>
#> [[6]][[5]]
#> x y time displacementTime polar
#> 1 28.29000 13.57800 0.00 0.00 28.29000+13.57800i
#> 2 27.81198 14.32895 0.02 0.02 27.81198+14.32895i
#> 3 27.40762 14.86050 0.04 0.04 27.40762+14.86050i
#> 4 27.03175 15.49091 0.06 0.06 27.03175+15.49091i
#> 5 26.56450 16.14424 0.08 0.08 26.56450+16.14424i
#> 6 26.26514 16.96626 0.10 0.10 26.26514+16.96626i
#> 7 25.84221 17.47308 0.12 0.12 25.84221+17.47308i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_5 Sim_6 TrajSim_5_6
#> 2 -0.4780245+0.7509549i Traj_5 Sim_6 TrajSim_5_6
#> 3 -0.4043593+0.5315462i Traj_5 Sim_6 TrajSim_5_6
#> 4 -0.3758681+0.6304135i Traj_5 Sim_6 TrajSim_5_6
#> 5 -0.4672471+0.6533271i Traj_5 Sim_6 TrajSim_5_6
#> 6 -0.2993622+0.8220204i Traj_5 Sim_6 TrajSim_5_6
#> 7 -0.4229258+0.5068129i Traj_5 Sim_6 TrajSim_5_6
#>
#> [[6]][[6]]
#> x y time displacementTime polar
#> 1 26.19800 13.69800 0.00 0.00 26.19800+13.69800i
#> 2 25.71843 14.68187 0.02 0.02 25.71843+14.68187i
#> 3 25.21269 15.74398 0.04 0.04 25.21269+15.74398i
#> 4 24.56802 16.67194 0.06 0.06 24.56802+16.67194i
#> 5 24.00002 17.63193 0.08 0.08 24.00002+17.63193i
#> 6 23.36348 18.51933 0.10 0.10 23.36348+18.51933i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_6 Sim_6 TrajSim_6_6
#> 2 -0.4795702+0.9838714i Traj_6 Sim_6 TrajSim_6_6
#> 3 -0.5057411+1.0621052i Traj_6 Sim_6 TrajSim_6_6
#> 4 -0.6446727+0.9279607i Traj_6 Sim_6 TrajSim_6_6
#> 5 -0.5679992+0.9599959i Traj_6 Sim_6 TrajSim_6_6
#> 6 -0.6365333+0.8873946i Traj_6 Sim_6 TrajSim_6_6
#>
#> [[6]][[7]]
#> x y time displacementTime polar
#> 1 26.47200 15.49600 0.00 0.00 26.47200+15.49600i
#> 2 27.65020 14.97689 0.02 0.02 27.65020+14.97689i
#> 3 28.97148 14.44366 0.04 0.04 28.97148+14.44366i
#> 4 29.89374 13.93015 0.06 0.06 29.89374+13.93015i
#> 5 31.01009 13.41081 0.08 0.08 31.01009+13.41081i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_7 Sim_6 TrajSim_7_6
#> 2 1.1781974-0.5191139i Traj_7 Sim_6 TrajSim_7_6
#> 3 1.3212833-0.5332250i Traj_7 Sim_6 TrajSim_7_6
#> 4 0.9222592-0.5135075i Traj_7 Sim_6 TrajSim_7_6
#> 5 1.1163466-0.5193415i Traj_7 Sim_6 TrajSim_7_6
#>
#> [[6]][[8]]
#> x y time displacementTime polar
#> 1 13.21800 8.752000 0.00 0.00 13.21800+8.752000i
#> 2 12.95737 8.460053 0.02 0.02 12.95737+8.460053i
#> 3 12.73240 8.130199 0.04 0.04 12.73240+8.130199i
#> 4 12.38750 7.861133 0.06 0.06 12.38750+7.861133i
#> 5 12.06313 7.629609 0.08 0.08 12.06313+7.629609i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_8 Sim_6 TrajSim_8_6
#> 2 -0.2606276-0.2919473i Traj_8 Sim_6 TrajSim_8_6
#> 3 -0.2249748-0.3298538i Traj_8 Sim_6 TrajSim_8_6
#> 4 -0.3448932-0.2690655i Traj_8 Sim_6 TrajSim_8_6
#> 5 -0.3243710-0.2315240i Traj_8 Sim_6 TrajSim_8_6
#>
#> [[6]][[9]]
#> x y time displacementTime polar
#> 1 15.63800 8.164000 0.00 0.00 15.63800+ 8.164000i
#> 2 15.14352 9.069738 0.02 0.02 15.14352+ 9.069738i
#> 3 14.82057 9.913260 0.04 0.04 14.82057+ 9.913260i
#> 4 14.40193 10.799955 0.06 0.06 14.40193+10.799955i
#> 5 13.97264 11.674253 0.08 0.08 13.97264+11.674253i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_9 Sim_6 TrajSim_9_6
#> 2 -0.4944810+0.9057377i Traj_9 Sim_6 TrajSim_9_6
#> 3 -0.3229445+0.8435228i Traj_9 Sim_6 TrajSim_9_6
#> 4 -0.4186436+0.8866946i Traj_9 Sim_6 TrajSim_9_6
#> 5 -0.4292900+0.8742980i Traj_9 Sim_6 TrajSim_9_6
#>
#> [[6]][[10]]
#> x y time displacementTime polar
#> 1 14.69800 6.798000 0.00 0.00 14.69800+ 6.798000i
#> 2 14.39904 7.662154 0.02 0.02 14.39904+ 7.662154i
#> 3 14.02847 8.432354 0.04 0.04 14.02847+ 8.432354i
#> 4 13.66220 9.169324 0.06 0.06 13.66220+ 9.169324i
#> 5 13.13953 10.023382 0.08 0.08 13.13953+10.023382i
#> 6 12.62430 10.752150 0.10 0.10 12.62430+10.752150i
#> 7 12.16171 11.642493 0.12 0.12 12.16171+11.642493i
#> 8 11.63509 12.447586 0.14 0.14 11.63509+12.447586i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_10 Sim_6 TrajSim_10_6
#> 2 -0.2989613+0.8641542i Traj_10 Sim_6 TrajSim_10_6
#> 3 -0.3705671+0.7701995i Traj_10 Sim_6 TrajSim_10_6
#> 4 -0.3662707+0.7369705i Traj_10 Sim_6 TrajSim_10_6
#> 5 -0.5226667+0.8540573i Traj_10 Sim_6 TrajSim_10_6
#> 6 -0.5152371+0.7287687i Traj_10 Sim_6 TrajSim_10_6
#> 7 -0.4625912+0.8903427i Traj_10 Sim_6 TrajSim_10_6
#> 8 -0.5266121+0.8050927i Traj_10 Sim_6 TrajSim_10_6
#>
#> [[6]][[11]]
#> x y time displacementTime polar
#> 1 12.00600 7.316000 0.00 0.00 12.00600+ 7.316000i
#> 2 11.64035 8.241127 0.02 0.02 11.64035+ 8.241127i
#> 3 11.21543 9.270483 0.04 0.04 11.21543+ 9.270483i
#> 4 10.83467 10.262522 0.06 0.06 10.83467+10.262522i
#> 5 10.46053 11.221164 0.08 0.08 10.46053+11.221164i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_11 Sim_6 TrajSim_11_6
#> 2 -0.3656505+0.9251273i Traj_11 Sim_6 TrajSim_11_6
#> 3 -0.4249188+1.0293556i Traj_11 Sim_6 TrajSim_11_6
#> 4 -0.3807582+0.9920388i Traj_11 Sim_6 TrajSim_11_6
#> 5 -0.3741409+0.9586420i Traj_11 Sim_6 TrajSim_11_6
#>
#>
#> [[7]]
#> [[7]][[1]]
#> x y time displacementTime polar
#> 1 36.88200 14.05600 0.00 0.00 36.88200+14.05600i
#> 2 36.21807 14.59219 0.02 0.02 36.21807+14.59219i
#> 3 35.67368 15.27678 0.04 0.04 35.67368+15.27678i
#> 4 35.06904 15.96989 0.06 0.06 35.06904+15.96989i
#> 5 34.49965 16.65460 0.08 0.08 34.49965+16.65460i
#> 6 33.81570 17.29370 0.10 0.10 33.81570+17.29370i
#> 7 33.11216 17.88659 0.12 0.12 33.11216+17.88659i
#> 8 32.52775 18.37966 0.14 0.14 32.52775+18.37966i
#> 9 31.82399 18.87311 0.16 0.16 31.82399+18.87311i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_1 Sim_7 TrajSim_1_7
#> 2 -0.6639322+0.5361910i Traj_1 Sim_7 TrajSim_1_7
#> 3 -0.5443920+0.6845880i Traj_1 Sim_7 TrajSim_1_7
#> 4 -0.6046374+0.6931096i Traj_1 Sim_7 TrajSim_1_7
#> 5 -0.5693837+0.6847140i Traj_1 Sim_7 TrajSim_1_7
#> 6 -0.6839548+0.6391022i Traj_1 Sim_7 TrajSim_1_7
#> 7 -0.7035393+0.5928856i Traj_1 Sim_7 TrajSim_1_7
#> 8 -0.5844067+0.4930687i Traj_1 Sim_7 TrajSim_1_7
#> 9 -0.7037643+0.4934524i Traj_1 Sim_7 TrajSim_1_7
#>
#> [[7]][[2]]
#> x y time displacementTime polar
#> 1 35.53200 13.51600 0.00 0.00 35.53200+13.51600i
#> 2 34.97669 14.31267 0.02 0.02 34.97669+14.31267i
#> 3 34.28119 15.07003 0.04 0.04 34.28119+15.07003i
#> 4 33.69559 15.69441 0.06 0.06 33.69559+15.69441i
#> 5 33.11556 16.43884 0.08 0.08 33.11556+16.43884i
#> 6 32.61502 17.25958 0.10 0.10 32.61502+17.25958i
#> 7 32.26142 18.10584 0.12 0.12 32.26142+18.10584i
#> 8 31.56442 18.84651 0.14 0.14 31.56442+18.84651i
#> 9 30.92582 19.54361 0.16 0.16 30.92582+19.54361i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_2 Sim_7 TrajSim_2_7
#> 2 -0.5553084+0.7966677i Traj_2 Sim_7 TrajSim_2_7
#> 3 -0.6955041+0.7573585i Traj_2 Sim_7 TrajSim_2_7
#> 4 -0.5855958+0.6243854i Traj_2 Sim_7 TrajSim_2_7
#> 5 -0.5800325+0.7444282i Traj_2 Sim_7 TrajSim_2_7
#> 6 -0.5005436+0.8207449i Traj_2 Sim_7 TrajSim_2_7
#> 7 -0.3535930+0.8462522i Traj_2 Sim_7 TrajSim_2_7
#> 8 -0.6969983+0.7406764i Traj_2 Sim_7 TrajSim_2_7
#> 9 -0.6386027+0.6971015i Traj_2 Sim_7 TrajSim_2_7
#>
#> [[7]][[3]]
#> x y time displacementTime polar
#> 1 34.54800 14.10000 0.00 0.00 34.54800+14.10000i
#> 2 33.80852 15.05512 0.02 0.02 33.80852+15.05512i
#> 3 32.99656 15.96440 0.04 0.04 32.99656+15.96440i
#> 4 32.16149 16.89227 0.06 0.06 32.16149+16.89227i
#> 5 31.36358 17.78241 0.08 0.08 31.36358+17.78241i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_3 Sim_7 TrajSim_3_7
#> 2 -0.7394817+0.9551182i Traj_3 Sim_7 TrajSim_3_7
#> 3 -0.8119627+0.9092815i Traj_3 Sim_7 TrajSim_3_7
#> 4 -0.8350627+0.9278745i Traj_3 Sim_7 TrajSim_3_7
#> 5 -0.7979168+0.8901310i Traj_3 Sim_7 TrajSim_3_7
#>
#> [[7]][[4]]
#> x y time displacementTime polar
#> 1 32.26000 14.51800 0.00 0.00 32.26000+14.51800i
#> 2 31.68613 15.46472 0.02 0.02 31.68613+15.46472i
#> 3 31.07522 16.28430 0.04 0.04 31.07522+16.28430i
#> 4 30.50092 17.25944 0.06 0.06 30.50092+17.25944i
#> 5 29.80760 18.14378 0.08 0.08 29.80760+18.14378i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_4 Sim_7 TrajSim_4_7
#> 2 -0.5738656+0.9467166i Traj_4 Sim_7 TrajSim_4_7
#> 3 -0.6109109+0.8195876i Traj_4 Sim_7 TrajSim_4_7
#> 4 -0.5742987+0.9751371i Traj_4 Sim_7 TrajSim_4_7
#> 5 -0.6933235+0.8843400i Traj_4 Sim_7 TrajSim_4_7
#>
#> [[7]][[5]]
#> x y time displacementTime polar
#> 1 28.29000 13.57800 0.00 0.00 28.29000+13.57800i
#> 2 27.71956 14.24249 0.02 0.02 27.71956+14.24249i
#> 3 27.30344 14.91045 0.04 0.04 27.30344+14.91045i
#> 4 26.90423 15.39689 0.06 0.06 26.90423+15.39689i
#> 5 26.39566 16.09809 0.08 0.08 26.39566+16.09809i
#> 6 25.92476 16.73605 0.10 0.10 25.92476+16.73605i
#> 7 25.53006 17.51461 0.12 0.12 25.53006+17.51461i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_5 Sim_7 TrajSim_5_7
#> 2 -0.5704416+0.6644854i Traj_5 Sim_7 TrajSim_5_7
#> 3 -0.4161201+0.6679691i Traj_5 Sim_7 TrajSim_5_7
#> 4 -0.3992121+0.4864311i Traj_5 Sim_7 TrajSim_5_7
#> 5 -0.5085620+0.7012053i Traj_5 Sim_7 TrajSim_5_7
#> 6 -0.4709059+0.6379547i Traj_5 Sim_7 TrajSim_5_7
#> 7 -0.3946974+0.7785664i Traj_5 Sim_7 TrajSim_5_7
#>
#> [[7]][[6]]
#> x y time displacementTime polar
#> 1 26.19800 13.69800 0.00 0.00 26.19800+13.69800i
#> 2 25.50170 14.71627 0.02 0.02 25.50170+14.71627i
#> 3 24.94302 15.59904 0.04 0.04 24.94302+15.59904i
#> 4 24.32816 16.55304 0.06 0.06 24.32816+16.55304i
#> 5 23.88682 17.46056 0.08 0.08 23.88682+17.46056i
#> 6 23.28158 18.44622 0.10 0.10 23.28158+18.44622i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_6 Sim_7 TrajSim_6_7
#> 2 -0.6962983+1.0182718i Traj_6 Sim_7 TrajSim_6_7
#> 3 -0.5586846+0.8827651i Traj_6 Sim_7 TrajSim_6_7
#> 4 -0.6148581+0.9540038i Traj_6 Sim_7 TrajSim_6_7
#> 5 -0.4413437+0.9075167i Traj_6 Sim_7 TrajSim_6_7
#> 6 -0.6052323+0.9856658i Traj_6 Sim_7 TrajSim_6_7
#>
#> [[7]][[7]]
#> x y time displacementTime polar
#> 1 26.47200 15.49600 0.00 0.00 26.47200+15.49600i
#> 2 27.63779 15.00256 0.02 0.02 27.63779+15.00256i
#> 3 28.59577 14.58060 0.04 0.04 28.59577+14.58060i
#> 4 29.88388 14.14874 0.06 0.06 29.88388+14.14874i
#> 5 31.07947 13.62273 0.08 0.08 31.07947+13.62273i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_7 Sim_7 TrajSim_7_7
#> 2 1.1657920-0.4934410i Traj_7 Sim_7 TrajSim_7_7
#> 3 0.9579752-0.4219623i Traj_7 Sim_7 TrajSim_7_7
#> 4 1.2881085-0.4318559i Traj_7 Sim_7 TrajSim_7_7
#> 5 1.1955991-0.5260104i Traj_7 Sim_7 TrajSim_7_7
#>
#> [[7]][[8]]
#> x y time displacementTime polar
#> 1 13.21800 8.752000 0.00 0.00 13.21800+8.752000i
#> 2 12.95245 8.421213 0.02 0.02 12.95245+8.421213i
#> 3 12.70529 8.144106 0.04 0.04 12.70529+8.144106i
#> 4 12.40344 7.924311 0.06 0.06 12.40344+7.924311i
#> 5 12.07912 7.655078 0.08 0.08 12.07912+7.655078i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_8 Sim_7 TrajSim_8_7
#> 2 -0.2655462-0.3307866i Traj_8 Sim_7 TrajSim_8_7
#> 3 -0.2471589-0.2771078i Traj_8 Sim_7 TrajSim_8_7
#> 4 -0.3018527-0.2197949i Traj_8 Sim_7 TrajSim_8_7
#> 5 -0.3243186-0.2692327i Traj_8 Sim_7 TrajSim_8_7
#>
#> [[7]][[9]]
#> x y time displacementTime polar
#> 1 15.63800 8.164000 0.00 0.00 15.63800+ 8.164000i
#> 2 15.23467 9.108452 0.02 0.02 15.23467+ 9.108452i
#> 3 14.68031 9.958619 0.04 0.04 14.68031+ 9.958619i
#> 4 14.20156 10.803668 0.06 0.06 14.20156+10.803668i
#> 5 13.63472 11.669404 0.08 0.08 13.63472+11.669404i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_9 Sim_7 TrajSim_9_7
#> 2 -0.4033252+0.9444520i Traj_9 Sim_7 TrajSim_9_7
#> 3 -0.5543612+0.8501669i Traj_9 Sim_7 TrajSim_9_7
#> 4 -0.4787495+0.8450486i Traj_9 Sim_7 TrajSim_9_7
#> 5 -0.5668432+0.8657368i Traj_9 Sim_7 TrajSim_9_7
#>
#> [[7]][[10]]
#> x y time displacementTime polar
#> 1 14.69800 6.798000 0.00 0.00 14.69800+ 6.798000i
#> 2 14.31376 7.513986 0.02 0.02 14.31376+ 7.513986i
#> 3 13.68572 8.262928 0.04 0.04 13.68572+ 8.262928i
#> 4 13.13290 9.017161 0.06 0.06 13.13290+ 9.017161i
#> 5 12.66224 9.735183 0.08 0.08 12.66224+ 9.735183i
#> 6 12.15334 10.423028 0.10 0.10 12.15334+10.423028i
#> 7 11.42653 11.090730 0.12 0.12 11.42653+11.090730i
#> 8 10.79780 11.709108 0.14 0.14 10.79780+11.709108i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_10 Sim_7 TrajSim_10_7
#> 2 -0.3842428+0.7159856i Traj_10 Sim_7 TrajSim_10_7
#> 3 -0.6280382+0.7489420i Traj_10 Sim_7 TrajSim_10_7
#> 4 -0.5528196+0.7542332i Traj_10 Sim_7 TrajSim_10_7
#> 5 -0.4706626+0.7180225i Traj_10 Sim_7 TrajSim_10_7
#> 6 -0.5088949+0.6878446i Traj_10 Sim_7 TrajSim_10_7
#> 7 -0.7268155+0.6677023i Traj_10 Sim_7 TrajSim_10_7
#> 8 -0.6287277+0.6183779i Traj_10 Sim_7 TrajSim_10_7
#>
#> [[7]][[11]]
#> x y time displacementTime polar
#> 1 12.00600 7.316000 0.00 0.00 12.00600+ 7.316000i
#> 2 11.60599 8.385218 0.02 0.02 11.60599+ 8.385218i
#> 3 11.14440 9.481190 0.04 0.04 11.14440+ 9.481190i
#> 4 10.75295 10.472521 0.06 0.06 10.75295+10.472521i
#> 5 10.41641 11.365069 0.08 0.08 10.41641+11.365069i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_11 Sim_7 TrajSim_11_7
#> 2 -0.4000087+1.0692176i Traj_11 Sim_7 TrajSim_11_7
#> 3 -0.4615939+1.0959721i Traj_11 Sim_7 TrajSim_11_7
#> 4 -0.3914437+0.9913314i Traj_11 Sim_7 TrajSim_11_7
#> 5 -0.3365452+0.8925475i Traj_11 Sim_7 TrajSim_11_7
#>
#>
#> [[8]]
#> [[8]][[1]]
#> x y time displacementTime polar
#> 1 36.88200 14.05600 0.00 0.00 36.88200+14.05600i
#> 2 36.16005 14.80141 0.02 0.02 36.16005+14.80141i
#> 3 35.51151 15.48503 0.04 0.04 35.51151+15.48503i
#> 4 34.98019 16.11669 0.06 0.06 34.98019+16.11669i
#> 5 34.32465 16.69521 0.08 0.08 34.32465+16.69521i
#> 6 33.54997 17.28749 0.10 0.10 33.54997+17.28749i
#> 7 32.90457 17.94798 0.12 0.12 32.90457+17.94798i
#> 8 32.34732 18.61825 0.14 0.14 32.34732+18.61825i
#> 9 31.79680 19.26478 0.16 0.16 31.79680+19.26478i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_1 Sim_8 TrajSim_1_8
#> 2 -0.7219493+0.7454096i Traj_1 Sim_8 TrajSim_1_8
#> 3 -0.6485384+0.6836223i Traj_1 Sim_8 TrajSim_1_8
#> 4 -0.5313212+0.6316610i Traj_1 Sim_8 TrajSim_1_8
#> 5 -0.6555440+0.5785136i Traj_1 Sim_8 TrajSim_1_8
#> 6 -0.7746722+0.5922864i Traj_1 Sim_8 TrajSim_1_8
#> 7 -0.6454008+0.6604875i Traj_1 Sim_8 TrajSim_1_8
#> 8 -0.5572577+0.6702683i Traj_1 Sim_8 TrajSim_1_8
#> 9 -0.5505135+0.6465274i Traj_1 Sim_8 TrajSim_1_8
#>
#> [[8]][[2]]
#> x y time displacementTime polar
#> 1 35.53200 13.51600 0.00 0.00 35.53200+13.51600i
#> 2 34.93753 14.27179 0.02 0.02 34.93753+14.27179i
#> 3 34.35094 15.15951 0.04 0.04 34.35094+15.15951i
#> 4 33.70222 15.95211 0.06 0.06 33.70222+15.95211i
#> 5 33.13375 16.56659 0.08 0.08 33.13375+16.56659i
#> 6 32.44639 17.24426 0.10 0.10 32.44639+17.24426i
#> 7 31.96311 17.88621 0.12 0.12 31.96311+17.88621i
#> 8 31.24917 18.51463 0.14 0.14 31.24917+18.51463i
#> 9 30.65820 19.30859 0.16 0.16 30.65820+19.30859i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_2 Sim_8 TrajSim_2_8
#> 2 -0.5944737+0.7557898i Traj_2 Sim_8 TrajSim_2_8
#> 3 -0.5865829+0.8877236i Traj_2 Sim_8 TrajSim_2_8
#> 4 -0.6487231+0.7925979i Traj_2 Sim_8 TrajSim_2_8
#> 5 -0.5684654+0.6144834i Traj_2 Sim_8 TrajSim_2_8
#> 6 -0.6873601+0.6776672i Traj_2 Sim_8 TrajSim_2_8
#> 7 -0.4832808+0.6419500i Traj_2 Sim_8 TrajSim_2_8
#> 8 -0.7139392+0.6284147i Traj_2 Sim_8 TrajSim_2_8
#> 9 -0.5909791+0.7939660i Traj_2 Sim_8 TrajSim_2_8
#>
#> [[8]][[3]]
#> x y time displacementTime polar
#> 1 34.54800 14.10000 0.00 0.00 34.54800+14.10000i
#> 2 33.76342 14.97145 0.02 0.02 33.76342+14.97145i
#> 3 33.09463 15.80108 0.04 0.04 33.09463+15.80108i
#> 4 32.32248 16.74615 0.06 0.06 32.32248+16.74615i
#> 5 31.57105 17.64337 0.08 0.08 31.57105+17.64337i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_3 Sim_8 TrajSim_3_8
#> 2 -0.7845779+0.8714489i Traj_3 Sim_8 TrajSim_3_8
#> 3 -0.6687915+0.8296333i Traj_3 Sim_8 TrajSim_3_8
#> 4 -0.7721506+0.9450646i Traj_3 Sim_8 TrajSim_3_8
#> 5 -0.7514318+0.8972247i Traj_3 Sim_8 TrajSim_3_8
#>
#> [[8]][[4]]
#> x y time displacementTime polar
#> 1 32.26000 14.51800 0.00 0.00 32.26000+14.51800i
#> 2 31.79910 15.40457 0.02 0.02 31.79910+15.40457i
#> 3 31.28433 16.29437 0.04 0.04 31.28433+16.29437i
#> 4 30.63832 17.20418 0.06 0.06 30.63832+17.20418i
#> 5 29.98550 17.95228 0.08 0.08 29.98550+17.95228i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_4 Sim_8 TrajSim_4_8
#> 2 -0.4608980+0.8865662i Traj_4 Sim_8 TrajSim_4_8
#> 3 -0.5147681+0.8898055i Traj_4 Sim_8 TrajSim_4_8
#> 4 -0.6460108+0.9098069i Traj_4 Sim_8 TrajSim_4_8
#> 5 -0.6528269+0.7481061i Traj_4 Sim_8 TrajSim_4_8
#>
#> [[8]][[5]]
#> x y time displacementTime polar
#> 1 28.29000 13.57800 0.00 0.00 28.29000+13.57800i
#> 2 27.83335 14.15986 0.02 0.02 27.83335+14.15986i
#> 3 27.64730 14.81237 0.04 0.04 27.64730+14.81237i
#> 4 27.20370 15.53694 0.06 0.06 27.20370+15.53694i
#> 5 26.78484 16.34751 0.08 0.08 26.78484+16.34751i
#> 6 26.20024 16.99117 0.10 0.10 26.20024+16.99117i
#> 7 25.94893 17.65504 0.12 0.12 25.94893+17.65504i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_5 Sim_8 TrajSim_5_8
#> 2 -0.4566486+0.5818582i Traj_5 Sim_8 TrajSim_5_8
#> 3 -0.1860494+0.6525159i Traj_5 Sim_8 TrajSim_5_8
#> 4 -0.4435994+0.7245696i Traj_5 Sim_8 TrajSim_5_8
#> 5 -0.4188656+0.8105653i Traj_5 Sim_8 TrajSim_5_8
#> 6 -0.5845972+0.6436631i Traj_5 Sim_8 TrajSim_5_8
#> 7 -0.2513057+0.6638634i Traj_5 Sim_8 TrajSim_5_8
#>
#> [[8]][[6]]
#> x y time displacementTime polar
#> 1 26.19800 13.69800 0.00 0.00 26.19800+13.69800i
#> 2 25.55489 14.60338 0.02 0.02 25.55489+14.60338i
#> 3 24.99167 15.67313 0.04 0.04 24.99167+15.67313i
#> 4 24.46885 16.57679 0.06 0.06 24.46885+16.57679i
#> 5 23.88380 17.53931 0.08 0.08 23.88380+17.53931i
#> 6 23.30444 18.50016 0.10 0.10 23.30444+18.50016i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_6 Sim_8 TrajSim_6_8
#> 2 -0.6431114+0.9053813i Traj_6 Sim_8 TrajSim_6_8
#> 3 -0.5632151+1.0697453i Traj_6 Sim_8 TrajSim_6_8
#> 4 -0.5228240+0.9036658i Traj_6 Sim_8 TrajSim_6_8
#> 5 -0.5850491+0.9625144i Traj_6 Sim_8 TrajSim_6_8
#> 6 -0.5793558+0.9608515i Traj_6 Sim_8 TrajSim_6_8
#>
#> [[8]][[7]]
#> x y time displacementTime polar
#> 1 26.47200 15.49600 0.00 0.00 26.47200+15.49600i
#> 2 27.76711 14.85215 0.02 0.02 27.76711+14.85215i
#> 3 28.73895 14.53375 0.04 0.04 28.73895+14.53375i
#> 4 29.94735 13.85537 0.06 0.06 29.94735+13.85537i
#> 5 31.15204 13.34913 0.08 0.08 31.15204+13.34913i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_7 Sim_8 TrajSim_7_8
#> 2 1.2951110-0.6438542i Traj_7 Sim_8 TrajSim_7_8
#> 3 0.9718417-0.3183950i Traj_7 Sim_8 TrajSim_7_8
#> 4 1.2083937-0.6783851i Traj_7 Sim_8 TrajSim_7_8
#> 5 1.2046986-0.5062323i Traj_7 Sim_8 TrajSim_7_8
#>
#> [[8]][[8]]
#> x y time displacementTime polar
#> 1 13.21800 8.752000 0.00 0.00 13.21800+8.752000i
#> 2 12.95097 8.467365 0.02 0.02 12.95097+8.467365i
#> 3 12.64593 8.242865 0.04 0.04 12.64593+8.242865i
#> 4 12.32552 7.990956 0.06 0.06 12.32552+7.990956i
#> 5 12.12167 7.690801 0.08 0.08 12.12167+7.690801i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_8 Sim_8 TrajSim_8_8
#> 2 -0.2670300-0.2846346i Traj_8 Sim_8 TrajSim_8_8
#> 3 -0.3050385-0.2245002i Traj_8 Sim_8 TrajSim_8_8
#> 4 -0.3204103-0.2519093i Traj_8 Sim_8 TrajSim_8_8
#> 5 -0.2038523-0.3001554i Traj_8 Sim_8 TrajSim_8_8
#>
#> [[8]][[9]]
#> x y time displacementTime polar
#> 1 15.63800 8.164000 0.00 0.00 15.63800+ 8.164000i
#> 2 15.22182 9.191309 0.02 0.02 15.22182+ 9.191309i
#> 3 14.75078 10.066487 0.04 0.04 14.75078+10.066487i
#> 4 14.25942 11.136908 0.06 0.06 14.25942+11.136908i
#> 5 13.84748 12.046462 0.08 0.08 13.84748+12.046462i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_9 Sim_8 TrajSim_9_8
#> 2 -0.4161765+1.0273091i Traj_9 Sim_8 TrajSim_9_8
#> 3 -0.4710393+0.8751778i Traj_9 Sim_8 TrajSim_9_8
#> 4 -0.4913668+1.0704208i Traj_9 Sim_8 TrajSim_9_8
#> 5 -0.4119340+0.9095546i Traj_9 Sim_8 TrajSim_9_8
#>
#> [[8]][[10]]
#> x y time displacementTime polar
#> 1 14.69800 6.798000 0.00 0.00 14.69800+ 6.798000i
#> 2 14.06247 7.513047 0.02 0.02 14.06247+ 7.513047i
#> 3 13.53776 8.345402 0.04 0.04 13.53776+ 8.345402i
#> 4 13.07251 9.104054 0.06 0.06 13.07251+ 9.104054i
#> 5 12.60539 9.883353 0.08 0.08 12.60539+ 9.883353i
#> 6 11.94392 10.710283 0.10 0.10 11.94392+10.710283i
#> 7 11.44044 11.452221 0.12 0.12 11.44044+11.452221i
#> 8 10.96321 12.251706 0.14 0.14 10.96321+12.251706i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_10 Sim_8 TrajSim_10_8
#> 2 -0.6355318+0.7150467i Traj_10 Sim_8 TrajSim_10_8
#> 3 -0.5247090+0.8323548i Traj_10 Sim_8 TrajSim_10_8
#> 4 -0.4652526+0.7586524i Traj_10 Sim_8 TrajSim_10_8
#> 5 -0.4671152+0.7792990i Traj_10 Sim_8 TrajSim_10_8
#> 6 -0.6614761+0.8269303i Traj_10 Sim_8 TrajSim_10_8
#> 7 -0.5034727+0.7419375i Traj_10 Sim_8 TrajSim_10_8
#> 8 -0.4772343+0.7994847i Traj_10 Sim_8 TrajSim_10_8
#>
#> [[8]][[11]]
#> x y time displacementTime polar
#> 1 12.00600 7.316000 0.00 0.00 12.00600+ 7.316000i
#> 2 11.74751 8.284508 0.02 0.02 11.74751+ 8.284508i
#> 3 11.38325 9.329565 0.04 0.04 11.38325+ 9.329565i
#> 4 10.87260 10.467840 0.06 0.06 10.87260+10.467840i
#> 5 10.45877 11.552544 0.08 0.08 10.45877+11.552544i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_11 Sim_8 TrajSim_11_8
#> 2 -0.2584906+0.9685084i Traj_11 Sim_8 TrajSim_11_8
#> 3 -0.3642564+1.0450566i Traj_11 Sim_8 TrajSim_11_8
#> 4 -0.5106568+1.1382751i Traj_11 Sim_8 TrajSim_11_8
#> 5 -0.4138305+1.0847040i Traj_11 Sim_8 TrajSim_11_8
#>
#>
#> [[9]]
#> [[9]][[1]]
#> x y time displacementTime polar
#> 1 36.88200 14.05600 0.00 0.00 36.88200+14.05600i
#> 2 36.29670 14.64367 0.02 0.02 36.29670+14.64367i
#> 3 35.60794 15.31225 0.04 0.04 35.60794+15.31225i
#> 4 35.07634 15.86261 0.06 0.06 35.07634+15.86261i
#> 5 34.52070 16.59384 0.08 0.08 34.52070+16.59384i
#> 6 33.89993 17.11313 0.10 0.10 33.89993+17.11313i
#> 7 33.09413 17.65816 0.12 0.12 33.09413+17.65816i
#> 8 32.53238 18.18410 0.14 0.14 32.53238+18.18410i
#> 9 31.87335 18.75877 0.16 0.16 31.87335+18.75877i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_1 Sim_9 TrajSim_1_9
#> 2 -0.5852996+0.5876655i Traj_1 Sim_9 TrajSim_1_9
#> 3 -0.6887564+0.6685882i Traj_1 Sim_9 TrajSim_1_9
#> 4 -0.5316044+0.5503565i Traj_1 Sim_9 TrajSim_1_9
#> 5 -0.5556439+0.7312304i Traj_1 Sim_9 TrajSim_1_9
#> 6 -0.6207620+0.5192867i Traj_1 Sim_9 TrajSim_1_9
#> 7 -0.8058029+0.5450333i Traj_1 Sim_9 TrajSim_1_9
#> 8 -0.5617517+0.5259421i Traj_1 Sim_9 TrajSim_1_9
#> 9 -0.6590283+0.5746636i Traj_1 Sim_9 TrajSim_1_9
#>
#> [[9]][[2]]
#> x y time displacementTime polar
#> 1 35.53200 13.51600 0.00 0.00 35.53200+13.51600i
#> 2 34.78939 14.23451 0.02 0.02 34.78939+14.23451i
#> 3 34.13209 14.91243 0.04 0.04 34.13209+14.91243i
#> 4 33.50584 15.54113 0.06 0.06 33.50584+15.54113i
#> 5 32.92392 16.31630 0.08 0.08 32.92392+16.31630i
#> 6 32.35457 16.99984 0.10 0.10 32.35457+16.99984i
#> 7 31.81292 17.72371 0.12 0.12 31.81292+17.72371i
#> 8 31.26982 18.46665 0.14 0.14 31.26982+18.46665i
#> 9 30.64765 19.26162 0.16 0.16 30.64765+19.26162i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_2 Sim_9 TrajSim_2_9
#> 2 -0.7426089+0.7185091i Traj_2 Sim_9 TrajSim_2_9
#> 3 -0.6573021+0.6779205i Traj_2 Sim_9 TrajSim_2_9
#> 4 -0.6262526+0.6286983i Traj_2 Sim_9 TrajSim_2_9
#> 5 -0.5819203+0.7751702i Traj_2 Sim_9 TrajSim_2_9
#> 6 -0.5693504+0.6835402i Traj_2 Sim_9 TrajSim_2_9
#> 7 -0.5416473+0.7238720i Traj_2 Sim_9 TrajSim_2_9
#> 8 -0.5431009+0.7429355i Traj_2 Sim_9 TrajSim_2_9
#> 9 -0.6221717+0.7949711i Traj_2 Sim_9 TrajSim_2_9
#>
#> [[9]][[3]]
#> x y time displacementTime polar
#> 1 34.54800 14.10000 0.00 0.00 34.54800+14.10000i
#> 2 33.74809 15.00940 0.02 0.02 33.74809+15.00940i
#> 3 32.74739 15.95585 0.04 0.04 32.74739+15.95585i
#> 4 32.18042 16.64266 0.06 0.06 32.18042+16.64266i
#> 5 31.44830 17.54669 0.08 0.08 31.44830+17.54669i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_3 Sim_9 TrajSim_3_9
#> 2 -0.7999063+0.9094031i Traj_3 Sim_9 TrajSim_3_9
#> 3 -1.0007065+0.9464484i Traj_3 Sim_9 TrajSim_3_9
#> 4 -0.5669631+0.6868073i Traj_3 Sim_9 TrajSim_3_9
#> 5 -0.7321204+0.9040272i Traj_3 Sim_9 TrajSim_3_9
#>
#> [[9]][[4]]
#> x y time displacementTime polar
#> 1 32.26000 14.51800 0.00 0.00 32.26000+14.51800i
#> 2 31.72083 15.25134 0.02 0.02 31.72083+15.25134i
#> 3 31.11708 16.05014 0.04 0.04 31.11708+16.05014i
#> 4 30.53145 16.96436 0.06 0.06 30.53145+16.96436i
#> 5 29.97449 17.77030 0.08 0.08 29.97449+17.77030i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_4 Sim_9 TrajSim_4_9
#> 2 -0.5391729+0.7333360i Traj_4 Sim_9 TrajSim_4_9
#> 3 -0.6037519+0.7987998i Traj_4 Sim_9 TrajSim_4_9
#> 4 -0.5856277+0.9142291i Traj_4 Sim_9 TrajSim_4_9
#> 5 -0.5569616+0.8059390i Traj_4 Sim_9 TrajSim_4_9
#>
#> [[9]][[5]]
#> x y time displacementTime polar
#> 1 28.29000 13.57800 0.00 0.00 28.29000+13.57800i
#> 2 28.00319 14.20424 0.02 0.02 28.00319+14.20424i
#> 3 27.63227 14.88811 0.04 0.04 27.63227+14.88811i
#> 4 27.38700 15.55552 0.06 0.06 27.38700+15.55552i
#> 5 27.11044 16.16450 0.08 0.08 27.11044+16.16450i
#> 6 26.79972 16.78097 0.10 0.10 26.79972+16.78097i
#> 7 26.17737 17.58073 0.12 0.12 26.17737+17.58073i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_5 Sim_9 TrajSim_5_9
#> 2 -0.2868111+0.6262392i Traj_5 Sim_9 TrajSim_5_9
#> 3 -0.3709197+0.6838718i Traj_5 Sim_9 TrajSim_5_9
#> 4 -0.2452660+0.6674052i Traj_5 Sim_9 TrajSim_5_9
#> 5 -0.2765635+0.6089872i Traj_5 Sim_9 TrajSim_5_9
#> 6 -0.3107196+0.6164677i Traj_5 Sim_9 TrajSim_5_9
#> 7 -0.6223499+0.7997636i Traj_5 Sim_9 TrajSim_5_9
#>
#> [[9]][[6]]
#> x y time displacementTime polar
#> 1 26.19800 13.69800 0.00 0.00 26.19800+13.69800i
#> 2 25.67155 14.60602 0.02 0.02 25.67155+14.60602i
#> 3 25.06466 15.52141 0.04 0.04 25.06466+15.52141i
#> 4 24.48895 16.30897 0.06 0.06 24.48895+16.30897i
#> 5 23.94633 17.28505 0.08 0.08 23.94633+17.28505i
#> 6 23.37747 18.07643 0.10 0.10 23.37747+18.07643i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_6 Sim_9 TrajSim_6_9
#> 2 -0.5264498+0.9080226i Traj_6 Sim_9 TrajSim_6_9
#> 3 -0.6068946+0.9153853i Traj_6 Sim_9 TrajSim_6_9
#> 4 -0.5757076+0.7875597i Traj_6 Sim_9 TrajSim_6_9
#> 5 -0.5426156+0.9760829i Traj_6 Sim_9 TrajSim_6_9
#> 6 -0.5688579+0.7913757i Traj_6 Sim_9 TrajSim_6_9
#>
#> [[9]][[7]]
#> x y time displacementTime polar
#> 1 26.47200 15.49600 0.00 0.00 26.47200+15.49600i
#> 2 27.53595 15.02956 0.02 0.02 27.53595+15.02956i
#> 3 28.72897 14.59559 0.04 0.04 28.72897+14.59559i
#> 4 29.91197 14.02230 0.06 0.06 29.91197+14.02230i
#> 5 30.98951 13.57299 0.08 0.08 30.98951+13.57299i
#> displacement Trajectory Simulation TrajSim
#> 1 0.000000+0.0000000i Traj_7 Sim_9 TrajSim_7_9
#> 2 1.063951-0.4664438i Traj_7 Sim_9 TrajSim_7_9
#> 3 1.193021-0.4339615i Traj_7 Sim_9 TrajSim_7_9
#> 4 1.182998-0.5732962i Traj_7 Sim_9 TrajSim_7_9
#> 5 1.077541-0.4493091i Traj_7 Sim_9 TrajSim_7_9
#>
#> [[9]][[8]]
#> x y time displacementTime polar
#> 1 13.21800 8.752000 0.00 0.00 13.21800+8.752000i
#> 2 12.86482 8.530979 0.02 0.02 12.86482+8.530979i
#> 3 12.59490 8.186213 0.04 0.04 12.59490+8.186213i
#> 4 12.40766 7.799013 0.06 0.06 12.40766+7.799013i
#> 5 12.17849 7.438475 0.08 0.08 12.17849+7.438475i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_8 Sim_9 TrajSim_8_9
#> 2 -0.3531804-0.2210212i Traj_8 Sim_9 TrajSim_8_9
#> 3 -0.2699208-0.3447663i Traj_8 Sim_9 TrajSim_8_9
#> 4 -0.1872402-0.3871991i Traj_8 Sim_9 TrajSim_8_9
#> 5 -0.2291648-0.3605383i Traj_8 Sim_9 TrajSim_8_9
#>
#> [[9]][[9]]
#> x y time displacementTime polar
#> 1 15.63800 8.164000 0.00 0.00 15.63800+ 8.164000i
#> 2 15.19531 9.006055 0.02 0.02 15.19531+ 9.006055i
#> 3 14.55630 9.815581 0.04 0.04 14.55630+ 9.815581i
#> 4 14.01310 10.695065 0.06 0.06 14.01310+10.695065i
#> 5 13.48281 11.575885 0.08 0.08 13.48281+11.575885i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_9 Sim_9 TrajSim_9_9
#> 2 -0.4426931+0.8420550i Traj_9 Sim_9 TrajSim_9_9
#> 3 -0.6390119+0.8095256i Traj_9 Sim_9 TrajSim_9_9
#> 4 -0.5431903+0.8794845i Traj_9 Sim_9 TrajSim_9_9
#> 5 -0.5302973+0.8808194i Traj_9 Sim_9 TrajSim_9_9
#>
#> [[9]][[10]]
#> x y time displacementTime polar
#> 1 14.69800 6.798000 0.00 0.00 14.69800+ 6.798000i
#> 2 14.43563 7.723599 0.02 0.02 14.43563+ 7.723599i
#> 3 13.86533 8.483953 0.04 0.04 13.86533+ 8.483953i
#> 4 13.28470 9.159932 0.06 0.06 13.28470+ 9.159932i
#> 5 12.66372 9.861669 0.08 0.08 12.66372+ 9.861669i
#> 6 12.21580 10.572421 0.10 0.10 12.21580+10.572421i
#> 7 11.53446 11.153088 0.12 0.12 11.53446+11.153088i
#> 8 11.04465 11.840148 0.14 0.14 11.04465+11.840148i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_10 Sim_9 TrajSim_10_9
#> 2 -0.2623722+0.9255993i Traj_10 Sim_9 TrajSim_10_9
#> 3 -0.5702989+0.7603532i Traj_10 Sim_9 TrajSim_10_9
#> 4 -0.5806301+0.6759793i Traj_10 Sim_9 TrajSim_10_9
#> 5 -0.6209829+0.7017368i Traj_10 Sim_9 TrajSim_10_9
#> 6 -0.4479154+0.7107526i Traj_10 Sim_9 TrajSim_10_9
#> 7 -0.6813411+0.5806669i Traj_10 Sim_9 TrajSim_10_9
#> 8 -0.4898062+0.6870603i Traj_10 Sim_9 TrajSim_10_9
#>
#> [[9]][[11]]
#> x y time displacementTime polar
#> 1 12.00600 7.316000 0.00 0.00 12.00600+ 7.316000i
#> 2 11.62366 8.322835 0.02 0.02 11.62366+ 8.322835i
#> 3 11.20923 9.341896 0.04 0.04 11.20923+ 9.341896i
#> 4 10.85213 10.399766 0.06 0.06 10.85213+10.399766i
#> 5 10.57350 11.549347 0.08 0.08 10.57350+11.549347i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.000000i Traj_11 Sim_9 TrajSim_11_9
#> 2 -0.3823440+1.006835i Traj_11 Sim_9 TrajSim_11_9
#> 3 -0.4144309+1.019062i Traj_11 Sim_9 TrajSim_11_9
#> 4 -0.3570967+1.057869i Traj_11 Sim_9 TrajSim_11_9
#> 5 -0.2786233+1.149581i Traj_11 Sim_9 TrajSim_11_9
#>
#>
#> [[10]]
#> [[10]][[1]]
#> x y time displacementTime polar
#> 1 36.88200 14.05600 0.00 0.00 36.88200+14.05600i
#> 2 36.04807 14.65395 0.02 0.02 36.04807+14.65395i
#> 3 35.41879 15.25806 0.04 0.04 35.41879+15.25806i
#> 4 34.82144 15.95585 0.06 0.06 34.82144+15.95585i
#> 5 34.22516 16.58776 0.08 0.08 34.22516+16.58776i
#> 6 33.57918 17.19974 0.10 0.10 33.57918+17.19974i
#> 7 32.79928 17.78331 0.12 0.12 32.79928+17.78331i
#> 8 32.06462 18.44949 0.14 0.14 32.06462+18.44949i
#> 9 31.41551 18.98844 0.16 0.16 31.41551+18.98844i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_1 Sim_10 TrajSim_1_10
#> 2 -0.8339265+0.5979513i Traj_1 Sim_10 TrajSim_1_10
#> 3 -0.6292875+0.6041087i Traj_1 Sim_10 TrajSim_1_10
#> 4 -0.5973453+0.6977879i Traj_1 Sim_10 TrajSim_1_10
#> 5 -0.5962771+0.6319141i Traj_1 Sim_10 TrajSim_1_10
#> 6 -0.6459796+0.6119812i Traj_1 Sim_10 TrajSim_1_10
#> 7 -0.7799054+0.5835688i Traj_1 Sim_10 TrajSim_1_10
#> 8 -0.7346561+0.6661770i Traj_1 Sim_10 TrajSim_1_10
#> 9 -0.6491132+0.5389541i Traj_1 Sim_10 TrajSim_1_10
#>
#> [[10]][[2]]
#> x y time displacementTime polar
#> 1 35.53200 13.51600 0.00 0.00 35.53200+13.51600i
#> 2 35.00062 14.29417 0.02 0.02 35.00062+14.29417i
#> 3 34.35913 14.89122 0.04 0.04 34.35913+14.89122i
#> 4 33.75963 15.66595 0.06 0.06 33.75963+15.66595i
#> 5 33.08975 16.25109 0.08 0.08 33.08975+16.25109i
#> 6 32.60578 16.97537 0.10 0.10 32.60578+16.97537i
#> 7 31.88525 17.78927 0.12 0.12 31.88525+17.78927i
#> 8 31.18457 18.49615 0.14 0.14 31.18457+18.49615i
#> 9 30.62757 19.22613 0.16 0.16 30.62757+19.22613i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_2 Sim_10 TrajSim_2_10
#> 2 -0.5313797+0.7781660i Traj_2 Sim_10 TrajSim_2_10
#> 3 -0.6414952+0.5970526i Traj_2 Sim_10 TrajSim_2_10
#> 4 -0.5994968+0.7747333i Traj_2 Sim_10 TrajSim_2_10
#> 5 -0.6698765+0.5851421i Traj_2 Sim_10 TrajSim_2_10
#> 6 -0.4839736+0.7242794i Traj_2 Sim_10 TrajSim_2_10
#> 7 -0.7205329+0.8138952i Traj_2 Sim_10 TrajSim_2_10
#> 8 -0.7006709+0.7068835i Traj_2 Sim_10 TrajSim_2_10
#> 9 -0.5570034+0.7299821i Traj_2 Sim_10 TrajSim_2_10
#>
#> [[10]][[3]]
#> x y time displacementTime polar
#> 1 34.54800 14.10000 0.00 0.00 34.54800+14.10000i
#> 2 33.74700 14.99175 0.02 0.02 33.74700+14.99175i
#> 3 33.09524 15.80340 0.04 0.04 33.09524+15.80340i
#> 4 32.30673 16.70720 0.06 0.06 32.30673+16.70720i
#> 5 31.47579 17.61430 0.08 0.08 31.47579+17.61430i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_3 Sim_10 TrajSim_3_10
#> 2 -0.8009988+0.8917499i Traj_3 Sim_10 TrajSim_3_10
#> 3 -0.6517576+0.8116493i Traj_3 Sim_10 TrajSim_3_10
#> 4 -0.7885132+0.9037971i Traj_3 Sim_10 TrajSim_3_10
#> 5 -0.8309430+0.9071030i Traj_3 Sim_10 TrajSim_3_10
#>
#> [[10]][[4]]
#> x y time displacementTime polar
#> 1 32.26000 14.51800 0.00 0.00 32.26000+14.51800i
#> 2 31.54327 15.40139 0.02 0.02 31.54327+15.40139i
#> 3 30.98488 16.16716 0.04 0.04 30.98488+16.16716i
#> 4 30.42242 17.00443 0.06 0.06 30.42242+17.00443i
#> 5 29.90972 17.76702 0.08 0.08 29.90972+17.76702i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_4 Sim_10 TrajSim_4_10
#> 2 -0.7167256+0.8833853i Traj_4 Sim_10 TrajSim_4_10
#> 3 -0.5583915+0.7657783i Traj_4 Sim_10 TrajSim_4_10
#> 4 -0.5624624+0.8372650i Traj_4 Sim_10 TrajSim_4_10
#> 5 -0.5126956+0.7625890i Traj_4 Sim_10 TrajSim_4_10
#>
#> [[10]][[5]]
#> x y time displacementTime polar
#> 1 28.29000 13.57800 0.00 0.00 28.29000+13.57800i
#> 2 27.72862 14.06663 0.02 0.02 27.72862+14.06663i
#> 3 27.39507 14.57510 0.04 0.04 27.39507+14.57510i
#> 4 26.93644 15.22270 0.06 0.06 26.93644+15.22270i
#> 5 26.44674 16.01623 0.08 0.08 26.44674+16.01623i
#> 6 26.15253 16.70659 0.10 0.10 26.15253+16.70659i
#> 7 25.72205 17.15773 0.12 0.12 25.72205+17.15773i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_5 Sim_10 TrajSim_5_10
#> 2 -0.5613824+0.4886336i Traj_5 Sim_10 TrajSim_5_10
#> 3 -0.3335479+0.5084687i Traj_5 Sim_10 TrajSim_5_10
#> 4 -0.4586338+0.6475991i Traj_5 Sim_10 TrajSim_5_10
#> 5 -0.4896958+0.7935335i Traj_5 Sim_10 TrajSim_5_10
#> 6 -0.2942122+0.6903523i Traj_5 Sim_10 TrajSim_5_10
#> 7 -0.4304815+0.4511468i Traj_5 Sim_10 TrajSim_5_10
#>
#> [[10]][[6]]
#> x y time displacementTime polar
#> 1 26.19800 13.69800 0.00 0.00 26.19800+13.69800i
#> 2 25.66063 14.66237 0.02 0.02 25.66063+14.66237i
#> 3 25.11143 15.50507 0.04 0.04 25.11143+15.50507i
#> 4 24.61646 16.31847 0.06 0.06 24.61646+16.31847i
#> 5 24.00011 17.22293 0.08 0.08 24.00011+17.22293i
#> 6 23.48608 18.08718 0.10 0.10 23.48608+18.08718i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_6 Sim_10 TrajSim_6_10
#> 2 -0.5373652+0.9643728i Traj_6 Sim_10 TrajSim_6_10
#> 3 -0.5492037+0.8427008i Traj_6 Sim_10 TrajSim_6_10
#> 4 -0.4949693+0.8133957i Traj_6 Sim_10 TrajSim_6_10
#> 5 -0.6163508+0.9044637i Traj_6 Sim_10 TrajSim_6_10
#> 6 -0.5140323+0.8642485i Traj_6 Sim_10 TrajSim_6_10
#>
#> [[10]][[7]]
#> x y time displacementTime polar
#> 1 26.47200 15.49600 0.00 0.00 26.47200+15.49600i
#> 2 27.50258 15.09730 0.02 0.02 27.50258+15.09730i
#> 3 28.73602 14.57530 0.04 0.04 28.73602+14.57530i
#> 4 29.95615 14.08560 0.06 0.06 29.95615+14.08560i
#> 5 31.08649 13.67815 0.08 0.08 31.08649+13.67815i
#> displacement Trajectory Simulation TrajSim
#> 1 0.000000+0.0000000i Traj_7 Sim_10 TrajSim_7_10
#> 2 1.030576-0.3987047i Traj_7 Sim_10 TrajSim_7_10
#> 3 1.233449-0.5219925i Traj_7 Sim_10 TrajSim_7_10
#> 4 1.220130-0.4897025i Traj_7 Sim_10 TrajSim_7_10
#> 5 1.130337-0.4074499i Traj_7 Sim_10 TrajSim_7_10
#>
#> [[10]][[8]]
#> x y time displacementTime polar
#> 1 13.21800 8.752000 0.00 0.00 13.21800+8.752000i
#> 2 12.97665 8.380473 0.02 0.02 12.97665+8.380473i
#> 3 12.80549 8.021363 0.04 0.04 12.80549+8.021363i
#> 4 12.45936 7.749821 0.06 0.06 12.45936+7.749821i
#> 5 12.22633 7.408041 0.08 0.08 12.22633+7.408041i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_8 Sim_10 TrajSim_8_10
#> 2 -0.2413543-0.3715266i Traj_8 Sim_10 TrajSim_8_10
#> 3 -0.1711597-0.3591100i Traj_8 Sim_10 TrajSim_8_10
#> 4 -0.3461232-0.2715427i Traj_8 Sim_10 TrajSim_8_10
#> 5 -0.2330317-0.3417794i Traj_8 Sim_10 TrajSim_8_10
#>
#> [[10]][[9]]
#> x y time displacementTime polar
#> 1 15.63800 8.164000 0.00 0.00 15.63800+ 8.164000i
#> 2 15.11892 8.955104 0.02 0.02 15.11892+ 8.955104i
#> 3 14.71854 9.909477 0.04 0.04 14.71854+ 9.909477i
#> 4 14.24447 10.812904 0.06 0.06 14.24447+10.812904i
#> 5 13.77281 11.733598 0.08 0.08 13.77281+11.733598i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_9 Sim_10 TrajSim_9_10
#> 2 -0.5190779+0.7911036i Traj_9 Sim_10 TrajSim_9_10
#> 3 -0.4003851+0.9543731i Traj_9 Sim_10 TrajSim_9_10
#> 4 -0.4740676+0.9034277i Traj_9 Sim_10 TrajSim_9_10
#> 5 -0.4716567+0.9206941i Traj_9 Sim_10 TrajSim_9_10
#>
#> [[10]][[10]]
#> x y time displacementTime polar
#> 1 14.69800 6.798000 0.00 0.00 14.69800+ 6.798000i
#> 2 14.10321 7.462628 0.02 0.02 14.10321+ 7.462628i
#> 3 13.46781 8.213721 0.04 0.04 13.46781+ 8.213721i
#> 4 12.85432 8.946931 0.06 0.06 12.85432+ 8.946931i
#> 5 12.53110 9.792059 0.08 0.08 12.53110+ 9.792059i
#> 6 11.92132 10.579520 0.10 0.10 11.92132+10.579520i
#> 7 11.45475 11.340102 0.12 0.12 11.45475+11.340102i
#> 8 10.86484 12.095058 0.14 0.14 10.86484+12.095058i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_10 Sim_10 TrajSim_10_10
#> 2 -0.5947934+0.6646280i Traj_10 Sim_10 TrajSim_10_10
#> 3 -0.6353941+0.7510929i Traj_10 Sim_10 TrajSim_10_10
#> 4 -0.6134875+0.7332096i Traj_10 Sim_10 TrajSim_10_10
#> 5 -0.3232234+0.8451283i Traj_10 Sim_10 TrajSim_10_10
#> 6 -0.6097841+0.7874613i Traj_10 Sim_10 TrajSim_10_10
#> 7 -0.4665674+0.7605816i Traj_10 Sim_10 TrajSim_10_10
#> 8 -0.5899109+0.7549564i Traj_10 Sim_10 TrajSim_10_10
#>
#> [[10]][[11]]
#> x y time displacementTime polar
#> 1 12.00600 7.316000 0.00 0.00 12.00600+ 7.316000i
#> 2 11.58396 8.268404 0.02 0.02 11.58396+ 8.268404i
#> 3 11.20675 9.284509 0.04 0.04 11.20675+ 9.284509i
#> 4 10.82124 10.259576 0.06 0.06 10.82124+10.259576i
#> 5 10.41150 11.204923 0.08 0.08 10.41150+11.204923i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_11 Sim_10 TrajSim_11_10
#> 2 -0.4220375+0.9524042i Traj_11 Sim_10 TrajSim_11_10
#> 3 -0.3772146+1.0161046i Traj_11 Sim_10 TrajSim_11_10
#> 4 -0.3855031+0.9750675i Traj_11 Sim_10 TrajSim_11_10
#> 5 -0.4097417+0.9453464i Traj_11 Sim_10 TrajSim_11_10
sim_constrained_mount <- simulate_track(sbMountTom, nsim = 100, model = "Constrained")
print(sim_constrained_mount[1:10])#> [[1]]
#> [[1]][[1]]
#> x y time displacementTime polar
#> 1 36.88200 14.05600 0.00 0.00 36.88200+14.05600i
#> 2 36.22828 14.58083 0.02 0.02 36.22828+14.58083i
#> 3 35.58632 15.16571 0.04 0.04 35.58632+15.16571i
#> 4 34.91863 15.81737 0.06 0.06 34.91863+15.81737i
#> 5 34.30602 16.43623 0.08 0.08 34.30602+16.43623i
#> 6 33.63828 17.01028 0.10 0.10 33.63828+17.01028i
#> 7 33.10329 17.65247 0.12 0.12 33.10329+17.65247i
#> 8 32.72339 18.33480 0.14 0.14 32.72339+18.33480i
#> 9 32.44050 19.03276 0.16 0.16 32.44050+19.03276i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_1 Sim_1 TrajSim_1_1
#> 2 -0.6537242+0.5248279i Traj_1 Sim_1 TrajSim_1_1
#> 3 -0.6419595+0.5848814i Traj_1 Sim_1 TrajSim_1_1
#> 4 -0.6676864+0.6516607i Traj_1 Sim_1 TrajSim_1_1
#> 5 -0.6126126+0.6188622i Traj_1 Sim_1 TrajSim_1_1
#> 6 -0.6677348+0.5740520i Traj_1 Sim_1 TrajSim_1_1
#> 7 -0.5349932+0.6421837i Traj_1 Sim_1 TrajSim_1_1
#> 8 -0.3798966+0.6823349i Traj_1 Sim_1 TrajSim_1_1
#> 9 -0.2828953+0.6979533i Traj_1 Sim_1 TrajSim_1_1
#>
#> [[1]][[2]]
#> x y time displacementTime polar
#> 1 35.53200 13.51600 0.00 0.00 35.53200+13.51600i
#> 2 34.95994 14.32372 0.02 0.02 34.95994+14.32372i
#> 3 34.51481 15.01780 0.04 0.04 34.51481+15.01780i
#> 4 33.84030 15.89817 0.06 0.06 33.84030+15.89817i
#> 5 33.21776 16.55317 0.08 0.08 33.21776+16.55317i
#> 6 32.67701 17.16547 0.10 0.10 32.67701+17.16547i
#> 7 32.00101 17.92328 0.12 0.12 32.00101+17.92328i
#> 8 31.34266 18.61650 0.14 0.14 31.34266+18.61650i
#> 9 30.74210 19.32719 0.16 0.16 30.74210+19.32719i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_2 Sim_1 TrajSim_2_1
#> 2 -0.5720557+0.8077209i Traj_2 Sim_1 TrajSim_2_1
#> 3 -0.4451379+0.6940798i Traj_2 Sim_1 TrajSim_2_1
#> 4 -0.6745105+0.8803720i Traj_2 Sim_1 TrajSim_2_1
#> 5 -0.6225371+0.6550021i Traj_2 Sim_1 TrajSim_2_1
#> 6 -0.5407467+0.6122915i Traj_2 Sim_1 TrajSim_2_1
#> 7 -0.6760070+0.7578121i Traj_2 Sim_1 TrajSim_2_1
#> 8 -0.6583420+0.6932221i Traj_2 Sim_1 TrajSim_2_1
#> 9 -0.6005628+0.7106907i Traj_2 Sim_1 TrajSim_2_1
#>
#> [[1]][[3]]
#> x y time displacementTime polar
#> 1 34.54800 14.10000 0.00 0.00 34.54800+14.10000i
#> 2 33.71853 15.05627 0.02 0.02 33.71853+15.05627i
#> 3 32.94707 15.97256 0.04 0.04 32.94707+15.97256i
#> 4 32.23929 16.78081 0.06 0.06 32.23929+16.78081i
#> 5 31.50740 17.63912 0.08 0.08 31.50740+17.63912i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_3 Sim_1 TrajSim_3_1
#> 2 -0.8294724+0.9562711i Traj_3 Sim_1 TrajSim_3_1
#> 3 -0.7714533+0.9162861i Traj_3 Sim_1 TrajSim_3_1
#> 4 -0.7077869+0.8082488i Traj_3 Sim_1 TrajSim_3_1
#> 5 -0.7318841+0.8583180i Traj_3 Sim_1 TrajSim_3_1
#>
#> [[1]][[4]]
#> x y time displacementTime polar
#> 1 32.26000 14.51800 0.00 0.00 32.26000+14.51800i
#> 2 31.60972 15.25388 0.02 0.02 31.60972+15.25388i
#> 3 31.03471 16.04731 0.04 0.04 31.03471+16.04731i
#> 4 30.37948 17.01940 0.06 0.06 30.37948+17.01940i
#> 5 29.83503 17.73170 0.08 0.08 29.83503+17.73170i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_4 Sim_1 TrajSim_4_1
#> 2 -0.6502771+0.7358793i Traj_4 Sim_1 TrajSim_4_1
#> 3 -0.5750159+0.7934265i Traj_4 Sim_1 TrajSim_4_1
#> 4 -0.6552276+0.9720929i Traj_4 Sim_1 TrajSim_4_1
#> 5 -0.5444520+0.7122999i Traj_4 Sim_1 TrajSim_4_1
#>
#> [[1]][[5]]
#> x y time displacementTime polar
#> 1 28.29000 13.57800 0.00 0.00 28.29000+13.57800i
#> 2 27.99146 14.11980 0.02 0.02 27.99146+14.11980i
#> 3 27.62550 14.75321 0.04 0.04 27.62550+14.75321i
#> 4 27.23154 15.33150 0.06 0.06 27.23154+15.33150i
#> 5 26.62338 16.12972 0.08 0.08 26.62338+16.12972i
#> 6 25.91981 16.65892 0.10 0.10 25.91981+16.65892i
#> 7 25.27247 17.16576 0.12 0.12 25.27247+17.16576i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_5 Sim_1 TrajSim_5_1
#> 2 -0.2985350+0.5418032i Traj_5 Sim_1 TrajSim_5_1
#> 3 -0.3659686+0.6334080i Traj_5 Sim_1 TrajSim_5_1
#> 4 -0.3939612+0.5782849i Traj_5 Sim_1 TrajSim_5_1
#> 5 -0.6081591+0.7982225i Traj_5 Sim_1 TrajSim_5_1
#> 6 -0.7035705+0.5292020i Traj_5 Sim_1 TrajSim_5_1
#> 7 -0.6473358+0.5068429i Traj_5 Sim_1 TrajSim_5_1
#>
#> [[1]][[6]]
#> x y time displacementTime polar
#> 1 26.19800 13.69800 0.00 0.00 26.19800+13.69800i
#> 2 25.65791 14.55278 0.02 0.02 25.65791+14.55278i
#> 3 25.07142 15.59119 0.04 0.04 25.07142+15.59119i
#> 4 24.54879 16.56873 0.06 0.06 24.54879+16.56873i
#> 5 24.19553 17.55995 0.08 0.08 24.19553+17.55995i
#> 6 23.80927 18.60023 0.10 0.10 23.80927+18.60023i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_6 Sim_1 TrajSim_6_1
#> 2 -0.5400928+0.8547847i Traj_6 Sim_1 TrajSim_6_1
#> 3 -0.5864869+1.0384014i Traj_6 Sim_1 TrajSim_6_1
#> 4 -0.5226305+0.9775481i Traj_6 Sim_1 TrajSim_6_1
#> 5 -0.3532586+0.9912123i Traj_6 Sim_1 TrajSim_6_1
#> 6 -0.3862612+1.0402788i Traj_6 Sim_1 TrajSim_6_1
#>
#> [[1]][[7]]
#> x y time displacementTime polar
#> 1 26.47200 15.49600 0.00 0.00 26.47200+15.49600i
#> 2 27.67841 15.08155 0.02 0.02 27.67841+15.08155i
#> 3 28.85926 14.64610 0.04 0.04 28.85926+14.64610i
#> 4 29.92786 14.26624 0.06 0.06 29.92786+14.26624i
#> 5 31.15573 13.82991 0.08 0.08 31.15573+13.82991i
#> displacement Trajectory Simulation TrajSim
#> 1 0.000000+0.0000000i Traj_7 Sim_1 TrajSim_7_1
#> 2 1.206414-0.4144501i Traj_7 Sim_1 TrajSim_7_1
#> 3 1.180849-0.4354511i Traj_7 Sim_1 TrajSim_7_1
#> 4 1.068599-0.3798577i Traj_7 Sim_1 TrajSim_7_1
#> 5 1.227867-0.4363362i Traj_7 Sim_1 TrajSim_7_1
#>
#> [[1]][[8]]
#> x y time displacementTime polar
#> 1 13.21800 8.752000 0.00 0.00 13.21800+8.752000i
#> 2 12.97970 8.471337 0.02 0.02 12.97970+8.471337i
#> 3 12.71963 8.144372 0.04 0.04 12.71963+8.144372i
#> 4 12.54573 7.808060 0.06 0.06 12.54573+7.808060i
#> 5 12.36222 7.408451 0.08 0.08 12.36222+7.408451i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_8 Sim_1 TrajSim_8_1
#> 2 -0.2383035-0.2806626i Traj_8 Sim_1 TrajSim_8_1
#> 3 -0.2600700-0.3269653i Traj_8 Sim_1 TrajSim_8_1
#> 4 -0.1738973-0.3363118i Traj_8 Sim_1 TrajSim_8_1
#> 5 -0.1835074-0.3996090i Traj_8 Sim_1 TrajSim_8_1
#>
#> [[1]][[9]]
#> x y time displacementTime polar
#> 1 15.63800 8.164000 0.00 0.00 15.63800+ 8.164000i
#> 2 15.04400 9.050677 0.02 0.02 15.04400+ 9.050677i
#> 3 14.44098 9.893285 0.04 0.04 14.44098+ 9.893285i
#> 4 13.72047 10.707361 0.06 0.06 13.72047+10.707361i
#> 5 12.96004 11.455234 0.08 0.08 12.96004+11.455234i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_9 Sim_1 TrajSim_9_1
#> 2 -0.5939970+0.8866774i Traj_9 Sim_1 TrajSim_9_1
#> 3 -0.6030265+0.8426075i Traj_9 Sim_1 TrajSim_9_1
#> 4 -0.7205057+0.8140764i Traj_9 Sim_1 TrajSim_9_1
#> 5 -0.7604346+0.7478724i Traj_9 Sim_1 TrajSim_9_1
#>
#> [[1]][[10]]
#> x y time displacementTime polar
#> 1 14.69800 6.798000 0.00 0.00 14.69800+ 6.798000i
#> 2 14.18385 7.578408 0.02 0.02 14.18385+ 7.578408i
#> 3 13.84146 8.275994 0.04 0.04 13.84146+ 8.275994i
#> 4 13.45154 9.123002 0.06 0.06 13.45154+ 9.123002i
#> 5 13.04152 9.908130 0.08 0.08 13.04152+ 9.908130i
#> 6 12.62467 10.687601 0.10 0.10 12.62467+10.687601i
#> 7 12.22256 11.377085 0.12 0.12 12.22256+11.377085i
#> 8 11.73190 12.127906 0.14 0.14 11.73190+12.127906i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_10 Sim_1 TrajSim_10_1
#> 2 -0.5141538+0.7804077i Traj_10 Sim_1 TrajSim_10_1
#> 3 -0.3423820+0.6975864i Traj_10 Sim_1 TrajSim_10_1
#> 4 -0.3899253+0.8470079i Traj_10 Sim_1 TrajSim_10_1
#> 5 -0.4100154+0.7851285i Traj_10 Sim_1 TrajSim_10_1
#> 6 -0.4168530+0.7794702i Traj_10 Sim_1 TrajSim_10_1
#> 7 -0.4021092+0.6894842i Traj_10 Sim_1 TrajSim_10_1
#> 8 -0.4906614+0.7508210i Traj_10 Sim_1 TrajSim_10_1
#>
#> [[1]][[11]]
#> x y time displacementTime polar
#> 1 12.00600 7.316000 0.00 0.00 12.00600+ 7.316000i
#> 2 11.56983 8.265959 0.02 0.02 11.56983+ 8.265959i
#> 3 11.15331 9.254561 0.04 0.04 11.15331+ 9.254561i
#> 4 10.71025 10.336132 0.06 0.06 10.71025+10.336132i
#> 5 10.34078 11.284384 0.08 0.08 10.34078+11.284384i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_11 Sim_1 TrajSim_11_1
#> 2 -0.4361698+0.9499594i Traj_11 Sim_1 TrajSim_11_1
#> 3 -0.4165176+0.9886015i Traj_11 Sim_1 TrajSim_11_1
#> 4 -0.4430636+1.0815712i Traj_11 Sim_1 TrajSim_11_1
#> 5 -0.3694726+0.9482520i Traj_11 Sim_1 TrajSim_11_1
#>
#>
#> [[2]]
#> [[2]][[1]]
#> x y time displacementTime polar
#> 1 36.88200 14.05600 0.00 0.00 36.88200+14.05600i
#> 2 36.27988 14.72322 0.02 0.02 36.27988+14.72322i
#> 3 35.67927 15.38152 0.04 0.04 35.67927+15.38152i
#> 4 35.01381 16.01482 0.06 0.06 35.01381+16.01482i
#> 5 34.37438 16.65304 0.08 0.08 34.37438+16.65304i
#> 6 33.64515 17.19706 0.10 0.10 33.64515+17.19706i
#> 7 32.79449 17.59413 0.12 0.12 32.79449+17.59413i
#> 8 32.05660 18.06156 0.14 0.14 32.05660+18.06156i
#> 9 31.36772 18.57834 0.16 0.16 31.36772+18.57834i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_1 Sim_2 TrajSim_1_2
#> 2 -0.6021182+0.6672172i Traj_1 Sim_2 TrajSim_1_2
#> 3 -0.6006103+0.6583064i Traj_1 Sim_2 TrajSim_1_2
#> 4 -0.6654641+0.6333004i Traj_1 Sim_2 TrajSim_1_2
#> 5 -0.6394320+0.6382131i Traj_1 Sim_2 TrajSim_1_2
#> 6 -0.7292219+0.5440208i Traj_1 Sim_2 TrajSim_1_2
#> 7 -0.8506663+0.3970764i Traj_1 Sim_2 TrajSim_1_2
#> 8 -0.7378850+0.4674225i Traj_1 Sim_2 TrajSim_1_2
#> 9 -0.6888852+0.5167783i Traj_1 Sim_2 TrajSim_1_2
#>
#> [[2]][[2]]
#> x y time displacementTime polar
#> 1 35.53200 13.51600 0.00 0.00 35.53200+13.51600i
#> 2 34.89484 14.11324 0.02 0.02 34.89484+14.11324i
#> 3 34.10746 14.69987 0.04 0.04 34.10746+14.69987i
#> 4 33.38110 15.23348 0.06 0.06 33.38110+15.23348i
#> 5 32.56105 15.91332 0.08 0.08 32.56105+15.91332i
#> 6 31.77919 16.47515 0.10 0.10 31.77919+16.47515i
#> 7 30.98554 17.20547 0.12 0.12 30.98554+17.20547i
#> 8 30.17434 17.99548 0.14 0.14 30.17434+17.99548i
#> 9 29.51222 18.73786 0.16 0.16 29.51222+18.73786i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_2 Sim_2 TrajSim_2_2
#> 2 -0.6371587+0.5972433i Traj_2 Sim_2 TrajSim_2_2
#> 3 -0.7873853+0.5866285i Traj_2 Sim_2 TrajSim_2_2
#> 4 -0.7263526+0.5336117i Traj_2 Sim_2 TrajSim_2_2
#> 5 -0.8200541+0.6798366i Traj_2 Sim_2 TrajSim_2_2
#> 6 -0.7818633+0.5618344i Traj_2 Sim_2 TrajSim_2_2
#> 7 -0.7936510+0.7303163i Traj_2 Sim_2 TrajSim_2_2
#> 8 -0.8111916+0.7900054i Traj_2 Sim_2 TrajSim_2_2
#> 9 -0.6621240+0.7423887i Traj_2 Sim_2 TrajSim_2_2
#>
#> [[2]][[3]]
#> x y time displacementTime polar
#> 1 34.54800 14.10000 0.00 0.00 34.54800+14.10000i
#> 2 33.74837 14.94334 0.02 0.02 33.74837+14.94334i
#> 3 33.11251 15.74669 0.04 0.04 33.11251+15.74669i
#> 4 32.55195 16.67988 0.06 0.06 32.55195+16.67988i
#> 5 31.92493 17.76337 0.08 0.08 31.92493+17.76337i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_3 Sim_2 TrajSim_3_2
#> 2 -0.7996330+0.8433399i Traj_3 Sim_2 TrajSim_3_2
#> 3 -0.6358537+0.8033519i Traj_3 Sim_2 TrajSim_3_2
#> 4 -0.5605647+0.9331863i Traj_3 Sim_2 TrajSim_3_2
#> 5 -0.6270234+1.0834965i Traj_3 Sim_2 TrajSim_3_2
#>
#> [[2]][[4]]
#> x y time displacementTime polar
#> 1 32.26000 14.51800 0.00 0.00 32.26000+14.51800i
#> 2 31.61696 15.36637 0.02 0.02 31.61696+15.36637i
#> 3 31.08778 16.14472 0.04 0.04 31.08778+16.14472i
#> 4 30.50012 16.99291 0.06 0.06 30.50012+16.99291i
#> 5 29.85420 17.80095 0.08 0.08 29.85420+17.80095i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_4 Sim_2 TrajSim_4_2
#> 2 -0.6430378+0.8483678i Traj_4 Sim_2 TrajSim_4_2
#> 3 -0.5291793+0.7783498i Traj_4 Sim_2 TrajSim_4_2
#> 4 -0.5876663+0.8481905i Traj_4 Sim_2 TrajSim_4_2
#> 5 -0.6459139+0.8080388i Traj_4 Sim_2 TrajSim_4_2
#>
#> [[2]][[5]]
#> x y time displacementTime polar
#> 1 28.29000 13.57800 0.00 0.00 28.29000+13.57800i
#> 2 27.62979 14.30142 0.02 0.02 27.62979+14.30142i
#> 3 27.00006 14.76503 0.04 0.04 27.00006+14.76503i
#> 4 26.55803 15.09059 0.06 0.06 26.55803+15.09059i
#> 5 25.90905 15.45458 0.08 0.08 25.90905+15.45458i
#> 6 25.10305 15.98761 0.10 0.10 25.10305+15.98761i
#> 7 24.54228 16.35000 0.12 0.12 24.54228+16.35000i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_5 Sim_2 TrajSim_5_2
#> 2 -0.6602129+0.7234215i Traj_5 Sim_2 TrajSim_5_2
#> 3 -0.6297291+0.4636113i Traj_5 Sim_2 TrajSim_5_2
#> 4 -0.4420288+0.3255614i Traj_5 Sim_2 TrajSim_5_2
#> 5 -0.6489774+0.3639904i Traj_5 Sim_2 TrajSim_5_2
#> 6 -0.8060058+0.5330298i Traj_5 Sim_2 TrajSim_5_2
#> 7 -0.5607647+0.3623824i Traj_5 Sim_2 TrajSim_5_2
#>
#> [[2]][[6]]
#> x y time displacementTime polar
#> 1 26.19800 13.69800 0.00 0.00 26.19800+13.69800i
#> 2 25.60039 14.52949 0.02 0.02 25.60039+14.52949i
#> 3 25.06789 15.47807 0.04 0.04 25.06789+15.47807i
#> 4 24.50774 16.33881 0.06 0.06 24.50774+16.33881i
#> 5 23.79948 17.18787 0.08 0.08 23.79948+17.18787i
#> 6 23.17802 17.89326 0.10 0.10 23.17802+17.89326i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_6 Sim_2 TrajSim_6_2
#> 2 -0.5976071+0.8314934i Traj_6 Sim_2 TrajSim_6_2
#> 3 -0.5325078+0.9485793i Traj_6 Sim_2 TrajSim_6_2
#> 4 -0.5601443+0.8607413i Traj_6 Sim_2 TrajSim_6_2
#> 5 -0.7082580+0.8490529i Traj_6 Sim_2 TrajSim_6_2
#> 6 -0.6214661+0.7053919i Traj_6 Sim_2 TrajSim_6_2
#>
#> [[2]][[7]]
#> x y time displacementTime polar
#> 1 26.47200 15.49600 0.00 0.00 26.47200+15.49600i
#> 2 27.56570 15.20750 0.02 0.02 27.56570+15.20750i
#> 3 28.88482 14.79019 0.04 0.04 28.88482+14.79019i
#> 4 30.08441 14.38866 0.06 0.06 30.08441+14.38866i
#> 5 31.11601 14.00634 0.08 0.08 31.11601+14.00634i
#> displacement Trajectory Simulation TrajSim
#> 1 0.000000+0.0000000i Traj_7 Sim_2 TrajSim_7_2
#> 2 1.093705-0.2885018i Traj_7 Sim_2 TrajSim_7_2
#> 3 1.319116-0.4173123i Traj_7 Sim_2 TrajSim_7_2
#> 4 1.199593-0.4015240i Traj_7 Sim_2 TrajSim_7_2
#> 5 1.031601-0.3823201i Traj_7 Sim_2 TrajSim_7_2
#>
#> [[2]][[8]]
#> x y time displacementTime polar
#> 1 13.21800 8.752000 0.00 0.00 13.21800+8.752000i
#> 2 12.96556 8.396405 0.02 0.02 12.96556+8.396405i
#> 3 12.67861 8.079443 0.04 0.04 12.67861+8.079443i
#> 4 12.42171 7.795845 0.06 0.06 12.42171+7.795845i
#> 5 12.06338 7.562844 0.08 0.08 12.06338+7.562844i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_8 Sim_2 TrajSim_8_2
#> 2 -0.2524383-0.3555954i Traj_8 Sim_2 TrajSim_8_2
#> 3 -0.2869510-0.3169615i Traj_8 Sim_2 TrajSim_8_2
#> 4 -0.2569007-0.2835984i Traj_8 Sim_2 TrajSim_8_2
#> 5 -0.3583328-0.2330012i Traj_8 Sim_2 TrajSim_8_2
#>
#> [[2]][[9]]
#> x y time displacementTime polar
#> 1 15.63800 8.164000 0.00 0.00 15.63800+ 8.164000i
#> 2 15.15243 9.090094 0.02 0.02 15.15243+ 9.090094i
#> 3 14.62995 10.028643 0.04 0.04 14.62995+10.028643i
#> 4 14.12488 10.991672 0.06 0.06 14.12488+10.991672i
#> 5 13.63124 11.970767 0.08 0.08 13.63124+11.970767i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_9 Sim_2 TrajSim_9_2
#> 2 -0.4855731+0.9260941i Traj_9 Sim_2 TrajSim_9_2
#> 3 -0.5224770+0.9385491i Traj_9 Sim_2 TrajSim_9_2
#> 4 -0.5050684+0.9630288i Traj_9 Sim_2 TrajSim_9_2
#> 5 -0.4936391+0.9790944i Traj_9 Sim_2 TrajSim_9_2
#>
#> [[2]][[10]]
#> x y time displacementTime polar
#> 1 14.69800 6.798000 0.00 0.00 14.69800+ 6.798000i
#> 2 14.20955 7.512851 0.02 0.02 14.20955+ 7.512851i
#> 3 13.70914 8.328175 0.04 0.04 13.70914+ 8.328175i
#> 4 13.26332 9.138676 0.06 0.06 13.26332+ 9.138676i
#> 5 12.63014 9.840556 0.08 0.08 12.63014+ 9.840556i
#> 6 12.08312 10.501358 0.10 0.10 12.08312+10.501358i
#> 7 11.43608 11.196707 0.12 0.12 11.43608+11.196707i
#> 8 10.91380 11.770601 0.14 0.14 10.91380+11.770601i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_10 Sim_2 TrajSim_10_2
#> 2 -0.4884497+0.7148512i Traj_10 Sim_2 TrajSim_10_2
#> 3 -0.5004121+0.8153236i Traj_10 Sim_2 TrajSim_10_2
#> 4 -0.4458192+0.8105014i Traj_10 Sim_2 TrajSim_10_2
#> 5 -0.6331811+0.7018802i Traj_10 Sim_2 TrajSim_10_2
#> 6 -0.5470214+0.6608020i Traj_10 Sim_2 TrajSim_10_2
#> 7 -0.6470317+0.6953483i Traj_10 Sim_2 TrajSim_10_2
#> 8 -0.5222822+0.5738940i Traj_10 Sim_2 TrajSim_10_2
#>
#> [[2]][[11]]
#> x y time displacementTime polar
#> 1 12.00600 7.316000 0.00 0.00 12.00600+ 7.316000i
#> 2 11.58329 8.455312 0.02 0.02 11.58329+ 8.455312i
#> 3 11.23118 9.297590 0.04 0.04 11.23118+ 9.297590i
#> 4 10.84062 10.239873 0.06 0.06 10.84062+10.239873i
#> 5 10.38931 11.241667 0.08 0.08 10.38931+11.241667i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_11 Sim_2 TrajSim_11_2
#> 2 -0.4227098+1.1393122i Traj_11 Sim_2 TrajSim_11_2
#> 3 -0.3521073+0.8422779i Traj_11 Sim_2 TrajSim_11_2
#> 4 -0.3905598+0.9422834i Traj_11 Sim_2 TrajSim_11_2
#> 5 -0.4513119+1.0017931i Traj_11 Sim_2 TrajSim_11_2
#>
#>
#> [[3]]
#> [[3]][[1]]
#> x y time displacementTime polar
#> 1 36.88200 14.05600 0.00 0.00 36.88200+14.05600i
#> 2 36.27616 14.68067 0.02 0.02 36.27616+14.68067i
#> 3 35.68733 15.36164 0.04 0.04 35.68733+15.36164i
#> 4 35.03638 16.09030 0.06 0.06 35.03638+16.09030i
#> 5 34.45233 16.86029 0.08 0.08 34.45233+16.86029i
#> 6 33.77211 17.51940 0.10 0.10 33.77211+17.51940i
#> 7 33.19824 18.06719 0.12 0.12 33.19824+18.06719i
#> 8 32.62013 18.75175 0.14 0.14 32.62013+18.75175i
#> 9 32.14838 19.52537 0.16 0.16 32.14838+19.52537i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_1 Sim_3 TrajSim_1_3
#> 2 -0.6058443+0.6246675i Traj_1 Sim_3 TrajSim_1_3
#> 3 -0.5888257+0.6809688i Traj_1 Sim_3 TrajSim_1_3
#> 4 -0.6509473+0.7286642i Traj_1 Sim_3 TrajSim_1_3
#> 5 -0.5840573+0.7699909i Traj_1 Sim_3 TrajSim_1_3
#> 6 -0.6802203+0.6591038i Traj_1 Sim_3 TrajSim_1_3
#> 7 -0.5738653+0.5477967i Traj_1 Sim_3 TrajSim_1_3
#> 8 -0.5781078+0.6845559i Traj_1 Sim_3 TrajSim_1_3
#> 9 -0.4717532+0.7736249i Traj_1 Sim_3 TrajSim_1_3
#>
#> [[3]][[2]]
#> x y time displacementTime polar
#> 1 35.53200 13.51600 0.00 0.00 35.53200+13.51600i
#> 2 34.90401 14.13278 0.02 0.02 34.90401+14.13278i
#> 3 34.15104 14.61194 0.04 0.04 34.15104+14.61194i
#> 4 33.28462 15.14701 0.06 0.06 33.28462+15.14701i
#> 5 32.46192 15.70477 0.08 0.08 32.46192+15.70477i
#> 6 31.68531 16.11097 0.10 0.10 31.68531+16.11097i
#> 7 30.82100 16.57211 0.12 0.12 30.82100+16.57211i
#> 8 30.10743 17.14231 0.14 0.14 30.10743+17.14231i
#> 9 29.48998 17.88895 0.16 0.16 29.48998+17.88895i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_2 Sim_3 TrajSim_2_3
#> 2 -0.6279949+0.6167798i Traj_2 Sim_3 TrajSim_2_3
#> 3 -0.7529661+0.4791644i Traj_2 Sim_3 TrajSim_2_3
#> 4 -0.8664229+0.5350705i Traj_2 Sim_3 TrajSim_2_3
#> 5 -0.8226927+0.5577504i Traj_2 Sim_3 TrajSim_2_3
#> 6 -0.7766165+0.4062008i Traj_2 Sim_3 TrajSim_2_3
#> 7 -0.8643076+0.4611418i Traj_2 Sim_3 TrajSim_2_3
#> 8 -0.7135696+0.5702038i Traj_2 Sim_3 TrajSim_2_3
#> 9 -0.6174542+0.7466347i Traj_2 Sim_3 TrajSim_2_3
#>
#> [[3]][[3]]
#> x y time displacementTime polar
#> 1 34.54800 14.10000 0.00 0.00 34.54800+14.10000i
#> 2 33.68385 15.09214 0.02 0.02 33.68385+15.09214i
#> 3 32.85744 16.11740 0.04 0.04 32.85744+16.11740i
#> 4 32.17193 16.98998 0.06 0.06 32.17193+16.98998i
#> 5 31.41999 17.94310 0.08 0.08 31.41999+17.94310i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_3 Sim_3 TrajSim_3_3
#> 2 -0.8641524+0.9921427i Traj_3 Sim_3 TrajSim_3_3
#> 3 -0.8264122+1.0252535i Traj_3 Sim_3 TrajSim_3_3
#> 4 -0.6855038+0.8725832i Traj_3 Sim_3 TrajSim_3_3
#> 5 -0.7519417+0.9531177i Traj_3 Sim_3 TrajSim_3_3
#>
#> [[3]][[4]]
#> x y time displacementTime polar
#> 1 32.26000 14.51800 0.00 0.00 32.26000+14.51800i
#> 2 31.63739 15.29634 0.02 0.02 31.63739+15.29634i
#> 3 31.14081 16.01008 0.04 0.04 31.14081+16.01008i
#> 4 30.60290 16.88488 0.06 0.06 30.60290+16.88488i
#> 5 30.25478 17.84541 0.08 0.08 30.25478+17.84541i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_4 Sim_3 TrajSim_4_3
#> 2 -0.6226081+0.7783354i Traj_4 Sim_3 TrajSim_4_3
#> 3 -0.4965848+0.7137453i Traj_4 Sim_3 TrajSim_4_3
#> 4 -0.5379047+0.8748031i Traj_4 Sim_3 TrajSim_4_3
#> 5 -0.3481241+0.9605281i Traj_4 Sim_3 TrajSim_4_3
#>
#> [[3]][[5]]
#> x y time displacementTime polar
#> 1 28.29000 13.57800 0.00 0.00 28.29000+13.57800i
#> 2 27.82177 14.44950 0.02 0.02 27.82177+14.44950i
#> 3 27.44520 15.10955 0.04 0.04 27.44520+15.10955i
#> 4 27.11370 15.80066 0.06 0.06 27.11370+15.80066i
#> 5 26.51154 16.54633 0.08 0.08 26.51154+16.54633i
#> 6 26.11124 17.07747 0.10 0.10 26.11124+17.07747i
#> 7 25.71738 17.71592 0.12 0.12 25.71738+17.71592i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_5 Sim_3 TrajSim_5_3
#> 2 -0.4682324+0.8715012i Traj_5 Sim_3 TrajSim_5_3
#> 3 -0.3765677+0.6600448i Traj_5 Sim_3 TrajSim_5_3
#> 4 -0.3314988+0.6911109i Traj_5 Sim_3 TrajSim_5_3
#> 5 -0.6021621+0.7456718i Traj_5 Sim_3 TrajSim_5_3
#> 6 -0.4003009+0.5311453i Traj_5 Sim_3 TrajSim_5_3
#> 7 -0.3938615+0.6384489i Traj_5 Sim_3 TrajSim_5_3
#>
#> [[3]][[6]]
#> x y time displacementTime polar
#> 1 26.19800 13.69800 0.00 0.00 26.19800+13.69800i
#> 2 25.61110 14.46879 0.02 0.02 25.61110+14.46879i
#> 3 24.90232 15.37495 0.04 0.04 24.90232+15.37495i
#> 4 24.18287 16.33449 0.06 0.06 24.18287+16.33449i
#> 5 23.59936 17.14314 0.08 0.08 23.59936+17.14314i
#> 6 22.88993 17.97103 0.10 0.10 22.88993+17.97103i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_6 Sim_3 TrajSim_6_3
#> 2 -0.5869038+0.7707920i Traj_6 Sim_3 TrajSim_6_3
#> 3 -0.7087805+0.9061619i Traj_6 Sim_3 TrajSim_6_3
#> 4 -0.7194422+0.9595314i Traj_6 Sim_3 TrajSim_6_3
#> 5 -0.5835103+0.8086504i Traj_6 Sim_3 TrajSim_6_3
#> 6 -0.7094330+0.8278992i Traj_6 Sim_3 TrajSim_6_3
#>
#> [[3]][[7]]
#> x y time displacementTime polar
#> 1 26.47200 15.49600 0.00 0.00 26.47200+15.49600i
#> 2 27.44328 15.15152 0.02 0.02 27.44328+15.15152i
#> 3 28.66874 14.59248 0.04 0.04 28.66874+14.59248i
#> 4 29.63240 14.15684 0.06 0.06 29.63240+14.15684i
#> 5 30.67327 13.60560 0.08 0.08 30.67327+13.60560i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_7 Sim_3 TrajSim_7_3
#> 2 0.9712845-0.3444786i Traj_7 Sim_3 TrajSim_7_3
#> 3 1.2254601-0.5590373i Traj_7 Sim_3 TrajSim_7_3
#> 4 0.9636567-0.4356450i Traj_7 Sim_3 TrajSim_7_3
#> 5 1.0408738-0.5512432i Traj_7 Sim_3 TrajSim_7_3
#>
#> [[3]][[8]]
#> x y time displacementTime polar
#> 1 13.21800 8.752000 0.00 0.00 13.21800+8.752000i
#> 2 12.96765 8.403903 0.02 0.02 12.96765+8.403903i
#> 3 12.65358 8.030849 0.04 0.04 12.65358+8.030849i
#> 4 12.35243 7.739454 0.06 0.06 12.35243+7.739454i
#> 5 12.09928 7.479757 0.08 0.08 12.09928+7.479757i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_8 Sim_3 TrajSim_8_3
#> 2 -0.2503456-0.3480965i Traj_8 Sim_3 TrajSim_8_3
#> 3 -0.3140738-0.3730543i Traj_8 Sim_3 TrajSim_8_3
#> 4 -0.3011515-0.2913957i Traj_8 Sim_3 TrajSim_8_3
#> 5 -0.2531526-0.2596967i Traj_8 Sim_3 TrajSim_8_3
#>
#> [[3]][[9]]
#> x y time displacementTime polar
#> 1 15.63800 8.164000 0.00 0.00 15.63800+ 8.164000i
#> 2 15.06062 8.966079 0.02 0.02 15.06062+ 8.966079i
#> 3 14.44366 9.716938 0.04 0.04 14.44366+ 9.716938i
#> 4 13.85107 10.544700 0.06 0.06 13.85107+10.544700i
#> 5 13.16738 11.324615 0.08 0.08 13.16738+11.324615i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_9 Sim_3 TrajSim_9_3
#> 2 -0.5773844+0.8020792i Traj_9 Sim_3 TrajSim_9_3
#> 3 -0.6169588+0.7508587i Traj_9 Sim_3 TrajSim_9_3
#> 4 -0.5925867+0.8277624i Traj_9 Sim_3 TrajSim_9_3
#> 5 -0.6836863+0.7799144i Traj_9 Sim_3 TrajSim_9_3
#>
#> [[3]][[10]]
#> x y time displacementTime polar
#> 1 14.69800 6.798000 0.00 0.00 14.69800+ 6.798000i
#> 2 14.13234 7.562666 0.02 0.02 14.13234+ 7.562666i
#> 3 13.59435 8.378026 0.04 0.04 13.59435+ 8.378026i
#> 4 13.05700 9.081235 0.06 0.06 13.05700+ 9.081235i
#> 5 12.46054 9.843208 0.08 0.08 12.46054+ 9.843208i
#> 6 11.82804 10.479935 0.10 0.10 11.82804+10.479935i
#> 7 11.26964 11.146212 0.12 0.12 11.26964+11.146212i
#> 8 10.62583 11.693407 0.14 0.14 10.62583+11.693407i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_10 Sim_3 TrajSim_10_3
#> 2 -0.5656615+0.7646659i Traj_10 Sim_3 TrajSim_10_3
#> 3 -0.5379837+0.8153603i Traj_10 Sim_3 TrajSim_10_3
#> 4 -0.5373570+0.7032085i Traj_10 Sim_3 TrajSim_10_3
#> 5 -0.5964593+0.7619733i Traj_10 Sim_3 TrajSim_10_3
#> 6 -0.6324970+0.6367273i Traj_10 Sim_3 TrajSim_10_3
#> 7 -0.5584024+0.6662772i Traj_10 Sim_3 TrajSim_10_3
#> 8 -0.6438124+0.5471945i Traj_10 Sim_3 TrajSim_10_3
#>
#> [[3]][[11]]
#> x y time displacementTime polar
#> 1 12.00600 7.316000 0.00 0.00 12.00600+ 7.316000i
#> 2 11.72055 8.378391 0.02 0.02 11.72055+ 8.378391i
#> 3 11.41417 9.414454 0.04 0.04 11.41417+ 9.414454i
#> 4 11.14248 10.467225 0.06 0.06 11.14248+10.467225i
#> 5 10.97440 11.329395 0.08 0.08 10.97440+11.329395i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_11 Sim_3 TrajSim_11_3
#> 2 -0.2854460+1.0623906i Traj_11 Sim_3 TrajSim_11_3
#> 3 -0.3063865+1.0360630i Traj_11 Sim_3 TrajSim_11_3
#> 4 -0.2716840+1.0527708i Traj_11 Sim_3 TrajSim_11_3
#> 5 -0.1680789+0.8621704i Traj_11 Sim_3 TrajSim_11_3
#>
#>
#> [[4]]
#> [[4]][[1]]
#> x y time displacementTime polar
#> 1 36.88200 14.05600 0.00 0.00 36.88200+14.05600i
#> 2 36.20427 14.69305 0.02 0.02 36.20427+14.69305i
#> 3 35.63676 15.33888 0.04 0.04 35.63676+15.33888i
#> 4 35.01468 15.98367 0.06 0.06 35.01468+15.98367i
#> 5 34.44061 16.64985 0.08 0.08 34.44061+16.64985i
#> 6 33.95353 17.35944 0.10 0.10 33.95353+17.35944i
#> 7 33.49708 18.04285 0.12 0.12 33.49708+18.04285i
#> 8 33.14928 18.81461 0.14 0.14 33.14928+18.81461i
#> 9 32.90525 19.71151 0.16 0.16 32.90525+19.71151i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_1 Sim_4 TrajSim_1_4
#> 2 -0.6777289+0.6370452i Traj_1 Sim_4 TrajSim_1_4
#> 3 -0.5675079+0.6458386i Traj_1 Sim_4 TrajSim_1_4
#> 4 -0.6220823+0.6447868i Traj_1 Sim_4 TrajSim_1_4
#> 5 -0.5740713+0.6661769i Traj_1 Sim_4 TrajSim_1_4
#> 6 -0.4870816+0.7095920i Traj_1 Sim_4 TrajSim_1_4
#> 7 -0.4564491+0.6834077i Traj_1 Sim_4 TrajSim_1_4
#> 8 -0.3478000+0.7717628i Traj_1 Sim_4 TrajSim_1_4
#> 9 -0.2440263+0.8968975i Traj_1 Sim_4 TrajSim_1_4
#>
#> [[4]][[2]]
#> x y time displacementTime polar
#> 1 35.53200 13.51600 0.00 0.00 35.53200+13.51600i
#> 2 34.95493 14.18116 0.02 0.02 34.95493+14.18116i
#> 3 34.32626 14.78068 0.04 0.04 34.32626+14.78068i
#> 4 33.66179 15.42311 0.06 0.06 33.66179+15.42311i
#> 5 32.87671 16.02556 0.08 0.08 32.87671+16.02556i
#> 6 31.99690 16.68303 0.10 0.10 31.99690+16.68303i
#> 7 31.15287 17.17798 0.12 0.12 31.15287+17.17798i
#> 8 30.26213 17.74184 0.14 0.14 30.26213+17.74184i
#> 9 29.37189 18.24164 0.16 0.16 29.37189+18.24164i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_2 Sim_4 TrajSim_2_4
#> 2 -0.5770657+0.6651637i Traj_2 Sim_4 TrajSim_2_4
#> 3 -0.6286742+0.5995159i Traj_2 Sim_4 TrajSim_2_4
#> 4 -0.6644659+0.6424272i Traj_2 Sim_4 TrajSim_2_4
#> 5 -0.7850816+0.6024569i Traj_2 Sim_4 TrajSim_2_4
#> 6 -0.8798119+0.6574677i Traj_2 Sim_4 TrajSim_2_4
#> 7 -0.8440276+0.4949514i Traj_2 Sim_4 TrajSim_2_4
#> 8 -0.8907387+0.5638566i Traj_2 Sim_4 TrajSim_2_4
#> 9 -0.8902448+0.4997983i Traj_2 Sim_4 TrajSim_2_4
#>
#> [[4]][[3]]
#> x y time displacementTime polar
#> 1 34.54800 14.10000 0.00 0.00 34.54800+14.10000i
#> 2 33.71504 15.10016 0.02 0.02 33.71504+15.10016i
#> 3 32.97883 15.97203 0.04 0.04 32.97883+15.97203i
#> 4 32.09808 16.97314 0.06 0.06 32.09808+16.97314i
#> 5 31.34685 17.93705 0.08 0.08 31.34685+17.93705i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_3 Sim_4 TrajSim_3_4
#> 2 -0.8329580+1.0001612i Traj_3 Sim_4 TrajSim_3_4
#> 3 -0.7362110+0.8718640i Traj_3 Sim_4 TrajSim_3_4
#> 4 -0.8807520+1.0011104i Traj_3 Sim_4 TrajSim_3_4
#> 5 -0.7512292+0.9639192i Traj_3 Sim_4 TrajSim_3_4
#>
#> [[4]][[4]]
#> x y time displacementTime polar
#> 1 32.26000 14.51800 0.00 0.00 32.26000+14.51800i
#> 2 31.61183 15.35158 0.02 0.02 31.61183+15.35158i
#> 3 30.95906 16.07192 0.04 0.04 30.95906+16.07192i
#> 4 30.26291 16.92914 0.06 0.06 30.26291+16.92914i
#> 5 29.58762 17.69048 0.08 0.08 29.58762+17.69048i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_4 Sim_4 TrajSim_4_4
#> 2 -0.6481652+0.8335754i Traj_4 Sim_4 TrajSim_4_4
#> 3 -0.6527726+0.7203427i Traj_4 Sim_4 TrajSim_4_4
#> 4 -0.6961553+0.8572224i Traj_4 Sim_4 TrajSim_4_4
#> 5 -0.6752880+0.7613382i Traj_4 Sim_4 TrajSim_4_4
#>
#> [[4]][[5]]
#> x y time displacementTime polar
#> 1 28.29000 13.57800 0.00 0.00 28.29000+13.57800i
#> 2 27.98073 14.30243 0.02 0.02 27.98073+14.30243i
#> 3 27.70746 15.06142 0.04 0.04 27.70746+15.06142i
#> 4 27.45003 15.54097 0.06 0.06 27.45003+15.54097i
#> 5 27.15894 16.25564 0.08 0.08 27.15894+16.25564i
#> 6 26.72124 17.13453 0.10 0.10 26.72124+17.13453i
#> 7 26.33400 17.94328 0.12 0.12 26.33400+17.94328i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_5 Sim_4 TrajSim_5_4
#> 2 -0.3092718+0.7244327i Traj_5 Sim_4 TrajSim_5_4
#> 3 -0.2732686+0.7589844i Traj_5 Sim_4 TrajSim_5_4
#> 4 -0.2574269+0.4795534i Traj_5 Sim_4 TrajSim_5_4
#> 5 -0.2910891+0.7146735i Traj_5 Sim_4 TrajSim_5_4
#> 6 -0.4377045+0.8788881i Traj_5 Sim_4 TrajSim_5_4
#> 7 -0.3872413+0.8087463i Traj_5 Sim_4 TrajSim_5_4
#>
#> [[4]][[6]]
#> x y time displacementTime polar
#> 1 26.19800 13.69800 0.00 0.00 26.19800+13.69800i
#> 2 25.64138 14.63724 0.02 0.02 25.64138+14.63724i
#> 3 25.24446 15.61664 0.04 0.04 25.24446+15.61664i
#> 4 24.94331 16.75831 0.06 0.06 24.94331+16.75831i
#> 5 24.76486 17.85640 0.08 0.08 24.76486+17.85640i
#> 6 24.71990 18.77387 0.10 0.10 24.71990+18.77387i
#> displacement Trajectory Simulation TrajSim
#> 1 0.00000000+0.0000000i Traj_6 Sim_4 TrajSim_6_4
#> 2 -0.55662382+0.9392430i Traj_6 Sim_4 TrajSim_6_4
#> 3 -0.39692096+0.9794017i Traj_6 Sim_4 TrajSim_6_4
#> 4 -0.30114132+1.1416638i Traj_6 Sim_4 TrajSim_6_4
#> 5 -0.17845589+1.0980911i Traj_6 Sim_4 TrajSim_6_4
#> 6 -0.04495667+0.9174679i Traj_6 Sim_4 TrajSim_6_4
#>
#> [[4]][[7]]
#> x y time displacementTime polar
#> 1 26.47200 15.49600 0.00 0.00 26.47200+15.49600i
#> 2 27.83863 15.04815 0.02 0.02 27.83863+15.04815i
#> 3 29.13387 14.57129 0.04 0.04 29.13387+14.57129i
#> 4 30.24025 14.23913 0.06 0.06 30.24025+14.23913i
#> 5 31.61117 13.95253 0.08 0.08 31.61117+13.95253i
#> displacement Trajectory Simulation TrajSim
#> 1 0.000000+0.0000000i Traj_7 Sim_4 TrajSim_7_4
#> 2 1.366626-0.4478476i Traj_7 Sim_4 TrajSim_7_4
#> 3 1.295247-0.4768601i Traj_7 Sim_4 TrajSim_7_4
#> 4 1.106375-0.3321580i Traj_7 Sim_4 TrajSim_7_4
#> 5 1.370926-0.2866019i Traj_7 Sim_4 TrajSim_7_4
#>
#> [[4]][[8]]
#> x y time displacementTime polar
#> 1 13.21800 8.752000 0.00 0.00 13.21800+8.752000i
#> 2 12.90586 8.563151 0.02 0.02 12.90586+8.563151i
#> 3 12.51341 8.339444 0.04 0.04 12.51341+8.339444i
#> 4 12.21014 8.147946 0.06 0.06 12.21014+8.147946i
#> 5 11.82401 8.035527 0.08 0.08 11.82401+8.035527i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_8 Sim_4 TrajSim_8_4
#> 2 -0.3121433-0.1888488i Traj_8 Sim_4 TrajSim_8_4
#> 3 -0.3924482-0.2237072i Traj_8 Sim_4 TrajSim_8_4
#> 4 -0.3032727-0.1914980i Traj_8 Sim_4 TrajSim_8_4
#> 5 -0.3861228-0.1124191i Traj_8 Sim_4 TrajSim_8_4
#>
#> [[4]][[9]]
#> x y time displacementTime polar
#> 1 15.63800 8.164000 0.00 0.00 15.63800+ 8.164000i
#> 2 15.14642 8.993346 0.02 0.02 15.14642+ 8.993346i
#> 3 14.42222 9.660446 0.04 0.04 14.42222+ 9.660446i
#> 4 13.62485 10.421953 0.06 0.06 13.62485+10.421953i
#> 5 12.98819 11.145904 0.08 0.08 12.98819+11.145904i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_9 Sim_4 TrajSim_9_4
#> 2 -0.4915838+0.8293462i Traj_9 Sim_4 TrajSim_9_4
#> 3 -0.7241935+0.6671003i Traj_9 Sim_4 TrajSim_9_4
#> 4 -0.7973692+0.7615065i Traj_9 Sim_4 TrajSim_9_4
#> 5 -0.6366658+0.7239508i Traj_9 Sim_4 TrajSim_9_4
#>
#> [[4]][[10]]
#> x y time displacementTime polar
#> 1 14.69800 6.798000 0.00 0.00 14.69800+ 6.798000i
#> 2 14.10480 7.577182 0.02 0.02 14.10480+ 7.577182i
#> 3 13.45931 8.344540 0.04 0.04 13.45931+ 8.344540i
#> 4 12.92110 9.042973 0.06 0.06 12.92110+ 9.042973i
#> 5 12.42094 9.775489 0.08 0.08 12.42094+ 9.775489i
#> 6 11.90427 10.615059 0.10 0.10 11.90427+10.615059i
#> 7 11.37476 11.277303 0.12 0.12 11.37476+11.277303i
#> 8 10.66859 11.941374 0.14 0.14 10.66859+11.941374i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_10 Sim_4 TrajSim_10_4
#> 2 -0.5932041+0.7791817i Traj_10 Sim_4 TrajSim_10_4
#> 3 -0.6454865+0.7673580i Traj_10 Sim_4 TrajSim_10_4
#> 4 -0.5382139+0.6984337i Traj_10 Sim_4 TrajSim_10_4
#> 5 -0.5001596+0.7325157i Traj_10 Sim_4 TrajSim_10_4
#> 6 -0.5166661+0.8395699i Traj_10 Sim_4 TrajSim_10_4
#> 7 -0.5295141+0.6622441i Traj_10 Sim_4 TrajSim_10_4
#> 8 -0.7061630+0.6640709i Traj_10 Sim_4 TrajSim_10_4
#>
#> [[4]][[11]]
#> x y time displacementTime polar
#> 1 12.00600 7.316000 0.00 0.00 12.00600+ 7.316000i
#> 2 11.66392 8.124436 0.02 0.02 11.66392+ 8.124436i
#> 3 11.27291 9.077281 0.04 0.04 11.27291+ 9.077281i
#> 4 10.81394 10.046393 0.06 0.06 10.81394+10.046393i
#> 5 10.35899 11.148103 0.08 0.08 10.35899+11.148103i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_11 Sim_4 TrajSim_11_4
#> 2 -0.3420793+0.8084365i Traj_11 Sim_4 TrajSim_11_4
#> 3 -0.3910073+0.9528441i Traj_11 Sim_4 TrajSim_11_4
#> 4 -0.4589732+0.9691126i Traj_11 Sim_4 TrajSim_11_4
#> 5 -0.4549547+1.1017093i Traj_11 Sim_4 TrajSim_11_4
#>
#>
#> [[5]]
#> [[5]][[1]]
#> x y time displacementTime polar
#> 1 36.88200 14.05600 0.00 0.00 36.88200+14.05600i
#> 2 36.25218 14.54095 0.02 0.02 36.25218+14.54095i
#> 3 35.56150 15.11934 0.04 0.04 35.56150+15.11934i
#> 4 34.91719 15.73913 0.06 0.06 34.91719+15.73913i
#> 5 34.23663 16.33664 0.08 0.08 34.23663+16.33664i
#> 6 33.52513 16.93279 0.10 0.10 33.52513+16.93279i
#> 7 32.85497 17.38433 0.12 0.12 32.85497+17.38433i
#> 8 32.19746 17.95977 0.14 0.14 32.19746+17.95977i
#> 9 31.46620 18.31029 0.16 0.16 31.46620+18.31029i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_1 Sim_5 TrajSim_1_5
#> 2 -0.6298166+0.4849538i Traj_1 Sim_5 TrajSim_1_5
#> 3 -0.6906868+0.5783863i Traj_1 Sim_5 TrajSim_1_5
#> 4 -0.6443034+0.6197885i Traj_1 Sim_5 TrajSim_1_5
#> 5 -0.6805633+0.5975126i Traj_1 Sim_5 TrajSim_1_5
#> 6 -0.7114998+0.5961455i Traj_1 Sim_5 TrajSim_1_5
#> 7 -0.6701614+0.4515405i Traj_1 Sim_5 TrajSim_1_5
#> 8 -0.6575044+0.5754382i Traj_1 Sim_5 TrajSim_1_5
#> 9 -0.7312668+0.3505266i Traj_1 Sim_5 TrajSim_1_5
#>
#> [[5]][[2]]
#> x y time displacementTime polar
#> 1 35.53200 13.51600 0.00 0.00 35.53200+13.51600i
#> 2 34.95239 14.27283 0.02 0.02 34.95239+14.27283i
#> 3 34.38950 14.98166 0.04 0.04 34.38950+14.98166i
#> 4 33.84835 15.73825 0.06 0.06 33.84835+15.73825i
#> 5 33.16017 16.46235 0.08 0.08 33.16017+16.46235i
#> 6 32.52830 17.13804 0.10 0.10 32.52830+17.13804i
#> 7 31.76087 17.82443 0.12 0.12 31.76087+17.82443i
#> 8 30.93654 18.32084 0.14 0.14 30.93654+18.32084i
#> 9 29.88502 18.81188 0.16 0.16 29.88502+18.81188i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_2 Sim_5 TrajSim_2_5
#> 2 -0.5796146+0.7568305i Traj_2 Sim_5 TrajSim_2_5
#> 3 -0.5628894+0.7088247i Traj_2 Sim_5 TrajSim_2_5
#> 4 -0.5411470+0.7565967i Traj_2 Sim_5 TrajSim_2_5
#> 5 -0.6881803+0.7240936i Traj_2 Sim_5 TrajSim_2_5
#> 6 -0.6318713+0.6756977i Traj_2 Sim_5 TrajSim_2_5
#> 7 -0.7674321+0.6863834i Traj_2 Sim_5 TrajSim_2_5
#> 8 -0.8243216+0.4964157i Traj_2 Sim_5 TrajSim_2_5
#> 9 -1.0515236+0.4910363i Traj_2 Sim_5 TrajSim_2_5
#>
#> [[5]][[3]]
#> x y time displacementTime polar
#> 1 34.54800 14.10000 0.00 0.00 34.54800+14.10000i
#> 2 33.84034 14.83581 0.02 0.02 33.84034+14.83581i
#> 3 33.04427 15.54049 0.04 0.04 33.04427+15.54049i
#> 4 32.13904 16.36861 0.06 0.06 32.13904+16.36861i
#> 5 31.34935 17.01535 0.08 0.08 31.34935+17.01535i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_3 Sim_5 TrajSim_3_5
#> 2 -0.7076638+0.7358113i Traj_3 Sim_5 TrajSim_3_5
#> 3 -0.7960708+0.7046749i Traj_3 Sim_5 TrajSim_3_5
#> 4 -0.9052252+0.8281262i Traj_3 Sim_5 TrajSim_3_5
#> 5 -0.7896898+0.6467326i Traj_3 Sim_5 TrajSim_3_5
#>
#> [[5]][[4]]
#> x y time displacementTime polar
#> 1 32.26000 14.51800 0.00 0.00 32.26000+14.51800i
#> 2 31.72982 15.27829 0.02 0.02 31.72982+15.27829i
#> 3 31.32983 16.31308 0.04 0.04 31.32983+16.31308i
#> 4 31.02981 17.33445 0.06 0.06 31.02981+17.33445i
#> 5 30.74322 18.20846 0.08 0.08 30.74322+18.20846i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_4 Sim_5 TrajSim_4_5
#> 2 -0.5301850+0.7602913i Traj_4 Sim_5 TrajSim_4_5
#> 3 -0.3999850+1.0347920i Traj_4 Sim_5 TrajSim_4_5
#> 4 -0.3000221+1.0213646i Traj_4 Sim_5 TrajSim_4_5
#> 5 -0.2865907+0.8740094i Traj_4 Sim_5 TrajSim_4_5
#>
#> [[5]][[5]]
#> x y time displacementTime polar
#> 1 28.29000 13.57800 0.00 0.00 28.29000+13.57800i
#> 2 27.88996 14.22843 0.02 0.02 27.88996+14.22843i
#> 3 27.52709 14.92063 0.04 0.04 27.52709+14.92063i
#> 4 27.13742 15.77631 0.06 0.06 27.13742+15.77631i
#> 5 26.81074 16.45792 0.08 0.08 26.81074+16.45792i
#> 6 26.39919 17.02731 0.10 0.10 26.39919+17.02731i
#> 7 25.94763 17.63140 0.12 0.12 25.94763+17.63140i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_5 Sim_5 TrajSim_5_5
#> 2 -0.4000422+0.6504308i Traj_5 Sim_5 TrajSim_5_5
#> 3 -0.3628728+0.6922027i Traj_5 Sim_5 TrajSim_5_5
#> 4 -0.3896615+0.8556747i Traj_5 Sim_5 TrajSim_5_5
#> 5 -0.3266805+0.6816114i Traj_5 Sim_5 TrajSim_5_5
#> 6 -0.4115491+0.5693925i Traj_5 Sim_5 TrajSim_5_5
#> 7 -0.4515656+0.6040844i Traj_5 Sim_5 TrajSim_5_5
#>
#> [[5]][[6]]
#> x y time displacementTime polar
#> 1 26.19800 13.69800 0.00 0.00 26.19800+13.69800i
#> 2 25.60101 14.53389 0.02 0.02 25.60101+14.53389i
#> 3 25.04462 15.33496 0.04 0.04 25.04462+15.33496i
#> 4 24.50825 16.34274 0.06 0.06 24.50825+16.34274i
#> 5 24.09678 17.36169 0.08 0.08 24.09678+17.36169i
#> 6 23.63984 18.29807 0.10 0.10 23.63984+18.29807i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_6 Sim_5 TrajSim_6_5
#> 2 -0.5969916+0.8358941i Traj_6 Sim_5 TrajSim_6_5
#> 3 -0.5563836+0.8010684i Traj_6 Sim_5 TrajSim_6_5
#> 4 -0.5363797+1.0077816i Traj_6 Sim_5 TrajSim_6_5
#> 5 -0.4114651+1.0189440i Traj_6 Sim_5 TrajSim_6_5
#> 6 -0.4569446+0.9363815i Traj_6 Sim_5 TrajSim_6_5
#>
#> [[5]][[7]]
#> x y time displacementTime polar
#> 1 26.47200 15.49600 0.00 0.00 26.47200+15.49600i
#> 2 27.50691 15.08541 0.02 0.02 27.50691+15.08541i
#> 3 28.76501 14.50188 0.04 0.04 28.76501+14.50188i
#> 4 29.80210 14.04122 0.06 0.06 29.80210+14.04122i
#> 5 31.00715 13.59421 0.08 0.08 31.00715+13.59421i
#> displacement Trajectory Simulation TrajSim
#> 1 0.000000+0.0000000i Traj_7 Sim_5 TrajSim_7_5
#> 2 1.034910-0.4105950i Traj_7 Sim_5 TrajSim_7_5
#> 3 1.258098-0.5835264i Traj_7 Sim_5 TrajSim_7_5
#> 4 1.037089-0.4606575i Traj_7 Sim_5 TrajSim_7_5
#> 5 1.205049-0.4470126i Traj_7 Sim_5 TrajSim_7_5
#>
#> [[5]][[8]]
#> x y time displacementTime polar
#> 1 13.21800 8.752000 0.00 0.00 13.21800+8.752000i
#> 2 12.95158 8.349261 0.02 0.02 12.95158+8.349261i
#> 3 12.69758 8.035373 0.04 0.04 12.69758+8.035373i
#> 4 12.43855 7.691362 0.06 0.06 12.43855+7.691362i
#> 5 12.16145 7.427285 0.08 0.08 12.16145+7.427285i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_8 Sim_5 TrajSim_8_5
#> 2 -0.2664164-0.4027394i Traj_8 Sim_5 TrajSim_8_5
#> 3 -0.2540073-0.3138878i Traj_8 Sim_5 TrajSim_8_5
#> 4 -0.2590227-0.3440104i Traj_8 Sim_5 TrajSim_8_5
#> 5 -0.2771045-0.2640778i Traj_8 Sim_5 TrajSim_8_5
#>
#> [[5]][[9]]
#> x y time displacementTime polar
#> 1 15.63800 8.164000 0.00 0.00 15.63800+ 8.164000i
#> 2 15.23164 9.078201 0.02 0.02 15.23164+ 9.078201i
#> 3 14.90225 10.006548 0.04 0.04 14.90225+10.006548i
#> 4 14.68691 10.959796 0.06 0.06 14.68691+10.959796i
#> 5 14.41770 11.979611 0.08 0.08 14.41770+11.979611i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_9 Sim_5 TrajSim_9_5
#> 2 -0.4063639+0.9142008i Traj_9 Sim_5 TrajSim_9_5
#> 3 -0.3293813+0.9283475i Traj_9 Sim_5 TrajSim_9_5
#> 4 -0.2153434+0.9532479i Traj_9 Sim_5 TrajSim_9_5
#> 5 -0.2692129+1.0198149i Traj_9 Sim_5 TrajSim_9_5
#>
#> [[5]][[10]]
#> x y time displacementTime polar
#> 1 14.69800 6.798000 0.00 0.00 14.69800+ 6.798000i
#> 2 14.13181 7.464298 0.02 0.02 14.13181+ 7.464298i
#> 3 13.61544 8.089145 0.04 0.04 13.61544+ 8.089145i
#> 4 12.96675 8.715000 0.06 0.06 12.96675+ 8.715000i
#> 5 12.34582 9.248404 0.08 0.08 12.34582+ 9.248404i
#> 6 11.67085 9.838793 0.10 0.10 11.67085+ 9.838793i
#> 7 11.07237 10.469352 0.12 0.12 11.07237+10.469352i
#> 8 10.46312 11.064647 0.14 0.14 10.46312+11.064647i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_10 Sim_5 TrajSim_10_5
#> 2 -0.5661886+0.6662979i Traj_10 Sim_5 TrajSim_10_5
#> 3 -0.5163762+0.6248472i Traj_10 Sim_5 TrajSim_10_5
#> 4 -0.6486830+0.6258549i Traj_10 Sim_5 TrajSim_10_5
#> 5 -0.6209338+0.5334041i Traj_10 Sim_5 TrajSim_10_5
#> 6 -0.6749700+0.5903888i Traj_10 Sim_5 TrajSim_10_5
#> 7 -0.5984821+0.6305594i Traj_10 Sim_5 TrajSim_10_5
#> 8 -0.6092420+0.5952951i Traj_10 Sim_5 TrajSim_10_5
#>
#> [[5]][[11]]
#> x y time displacementTime polar
#> 1 12.00600 7.316000 0.00 0.00 12.00600+ 7.316000i
#> 2 11.57769 8.399799 0.02 0.02 11.57769+ 8.399799i
#> 3 11.06339 9.391720 0.04 0.04 11.06339+ 9.391720i
#> 4 10.52276 10.409895 0.06 0.06 10.52276+10.409895i
#> 5 10.06674 11.269222 0.08 0.08 10.06674+11.269222i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_11 Sim_5 TrajSim_11_5
#> 2 -0.4283140+1.0837993i Traj_11 Sim_5 TrajSim_11_5
#> 3 -0.5142972+0.9919210i Traj_11 Sim_5 TrajSim_11_5
#> 4 -0.5406256+1.0181744i Traj_11 Sim_5 TrajSim_11_5
#> 5 -0.4560239+0.8593273i Traj_11 Sim_5 TrajSim_11_5
#>
#>
#> [[6]]
#> [[6]][[1]]
#> x y time displacementTime polar
#> 1 36.88200 14.05600 0.00 0.00 36.88200+14.05600i
#> 2 36.26689 14.57475 0.02 0.02 36.26689+14.57475i
#> 3 35.65650 15.01058 0.04 0.04 35.65650+15.01058i
#> 4 34.91193 15.49908 0.06 0.06 34.91193+15.49908i
#> 5 34.08756 15.84688 0.08 0.08 34.08756+15.84688i
#> 6 33.34486 16.15563 0.10 0.10 33.34486+16.15563i
#> 7 32.53223 16.50857 0.12 0.12 32.53223+16.50857i
#> 8 31.67584 16.84878 0.14 0.14 31.67584+16.84878i
#> 9 30.92538 17.37820 0.16 0.16 30.92538+17.37820i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_1 Sim_6 TrajSim_1_6
#> 2 -0.6151101+0.5187472i Traj_1 Sim_6 TrajSim_1_6
#> 3 -0.6103887+0.4358349i Traj_1 Sim_6 TrajSim_1_6
#> 4 -0.7445672+0.4884946i Traj_1 Sim_6 TrajSim_1_6
#> 5 -0.8243726+0.3478038i Traj_1 Sim_6 TrajSim_1_6
#> 6 -0.7427052+0.3087453i Traj_1 Sim_6 TrajSim_1_6
#> 7 -0.8126275+0.3529431i Traj_1 Sim_6 TrajSim_1_6
#> 8 -0.8563875+0.3402160i Traj_1 Sim_6 TrajSim_1_6
#> 9 -0.7504655+0.5294198i Traj_1 Sim_6 TrajSim_1_6
#>
#> [[6]][[2]]
#> x y time displacementTime polar
#> 1 35.53200 13.51600 0.00 0.00 35.53200+13.51600i
#> 2 34.90627 14.21011 0.02 0.02 34.90627+14.21011i
#> 3 34.23091 14.88856 0.04 0.04 34.23091+14.88856i
#> 4 33.64026 15.63854 0.06 0.06 33.64026+15.63854i
#> 5 33.23290 16.41839 0.08 0.08 33.23290+16.41839i
#> 6 32.80498 17.31224 0.10 0.10 32.80498+17.31224i
#> 7 32.42508 18.25173 0.12 0.12 32.42508+18.25173i
#> 8 32.01707 19.14632 0.14 0.14 32.01707+19.14632i
#> 9 31.51268 20.06452 0.16 0.16 31.51268+20.06452i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_2 Sim_6 TrajSim_2_6
#> 2 -0.6257287+0.6941146i Traj_2 Sim_6 TrajSim_2_6
#> 3 -0.6753661+0.6784414i Traj_2 Sim_6 TrajSim_2_6
#> 4 -0.5906455+0.7499850i Traj_2 Sim_6 TrajSim_2_6
#> 5 -0.4073562+0.7798470i Traj_2 Sim_6 TrajSim_2_6
#> 6 -0.4279283+0.8938558i Traj_2 Sim_6 TrajSim_2_6
#> 7 -0.3798992+0.9394813i Traj_2 Sim_6 TrajSim_2_6
#> 8 -0.4080030+0.8945901i Traj_2 Sim_6 TrajSim_2_6
#> 9 -0.5043919+0.9182096i Traj_2 Sim_6 TrajSim_2_6
#>
#> [[6]][[3]]
#> x y time displacementTime polar
#> 1 34.54800 14.10000 0.00 0.00 34.54800+14.10000i
#> 2 33.71033 15.04659 0.02 0.02 33.71033+15.04659i
#> 3 32.83500 15.91161 0.04 0.04 32.83500+15.91161i
#> 4 32.00265 16.73277 0.06 0.06 32.00265+16.73277i
#> 5 31.30958 17.48385 0.08 0.08 31.30958+17.48385i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_3 Sim_6 TrajSim_3_6
#> 2 -0.8376718+0.9465876i Traj_3 Sim_6 TrajSim_3_6
#> 3 -0.8753302+0.8650203i Traj_3 Sim_6 TrajSim_3_6
#> 4 -0.8323459+0.8211631i Traj_3 Sim_6 TrajSim_3_6
#> 5 -0.6930749+0.7510800i Traj_3 Sim_6 TrajSim_3_6
#>
#> [[6]][[4]]
#> x y time displacementTime polar
#> 1 32.26000 14.51800 0.00 0.00 32.26000+14.51800i
#> 2 31.57310 15.29516 0.02 0.02 31.57310+15.29516i
#> 3 30.89623 16.00744 0.04 0.04 30.89623+16.00744i
#> 4 30.16432 16.78392 0.06 0.06 30.16432+16.78392i
#> 5 29.37035 17.52520 0.08 0.08 29.37035+17.52520i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_4 Sim_6 TrajSim_4_6
#> 2 -0.6868996+0.7771559i Traj_4 Sim_6 TrajSim_4_6
#> 3 -0.6768667+0.7122813i Traj_4 Sim_6 TrajSim_4_6
#> 4 -0.7319185+0.7764789i Traj_4 Sim_6 TrajSim_4_6
#> 5 -0.7939665+0.7412831i Traj_4 Sim_6 TrajSim_4_6
#>
#> [[6]][[5]]
#> x y time displacementTime polar
#> 1 28.29000 13.57800 0.00 0.00 28.29000+13.57800i
#> 2 27.84002 14.40143 0.02 0.02 27.84002+14.40143i
#> 3 27.52205 15.01308 0.04 0.04 27.52205+15.01308i
#> 4 27.17573 15.86634 0.06 0.06 27.17573+15.86634i
#> 5 26.70331 16.56700 0.08 0.08 26.70331+16.56700i
#> 6 26.23792 17.06673 0.10 0.10 26.23792+17.06673i
#> 7 25.72292 17.61256 0.12 0.12 25.72292+17.61256i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_5 Sim_6 TrajSim_5_6
#> 2 -0.4499774+0.8234326i Traj_5 Sim_6 TrajSim_5_6
#> 3 -0.3179686+0.6116457i Traj_5 Sim_6 TrajSim_5_6
#> 4 -0.3463221+0.8532578i Traj_5 Sim_6 TrajSim_5_6
#> 5 -0.4724253+0.7006651i Traj_5 Sim_6 TrajSim_5_6
#> 6 -0.4653853+0.4997306i Traj_5 Sim_6 TrajSim_5_6
#> 7 -0.5150039+0.5458249i Traj_5 Sim_6 TrajSim_5_6
#>
#> [[6]][[6]]
#> x y time displacementTime polar
#> 1 26.19800 13.69800 0.00 0.00 26.19800+13.69800i
#> 2 25.68867 14.78619 0.02 0.02 25.68867+14.78619i
#> 3 25.17543 15.81702 0.04 0.04 25.17543+15.81702i
#> 4 24.57746 16.71745 0.06 0.06 24.57746+16.71745i
#> 5 23.99572 17.68691 0.08 0.08 23.99572+17.68691i
#> 6 23.54903 18.57414 0.10 0.10 23.54903+18.57414i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_6 Sim_6 TrajSim_6_6
#> 2 -0.5093347+1.0881875i Traj_6 Sim_6 TrajSim_6_6
#> 3 -0.5132394+1.0308366i Traj_6 Sim_6 TrajSim_6_6
#> 4 -0.5979676+0.9004243i Traj_6 Sim_6 TrajSim_6_6
#> 5 -0.5817404+0.9694606i Traj_6 Sim_6 TrajSim_6_6
#> 6 -0.4466914+0.8872348i Traj_6 Sim_6 TrajSim_6_6
#>
#> [[6]][[7]]
#> x y time displacementTime polar
#> 1 26.47200 15.49600 0.00 0.00 26.47200+15.49600i
#> 2 27.57570 15.09637 0.02 0.02 27.57570+15.09637i
#> 3 28.85011 14.58009 0.04 0.04 28.85011+14.58009i
#> 4 30.10343 14.19567 0.06 0.06 30.10343+14.19567i
#> 5 31.23276 13.91941 0.08 0.08 31.23276+13.91941i
#> displacement Trajectory Simulation TrajSim
#> 1 0.000000+0.0000000i Traj_7 Sim_6 TrajSim_7_6
#> 2 1.103701-0.3996338i Traj_7 Sim_6 TrajSim_7_6
#> 3 1.274405-0.5162760i Traj_7 Sim_6 TrajSim_7_6
#> 4 1.253322-0.3844157i Traj_7 Sim_6 TrajSim_7_6
#> 5 1.129328-0.2762597i Traj_7 Sim_6 TrajSim_7_6
#>
#> [[6]][[8]]
#> x y time displacementTime polar
#> 1 13.21800 8.752000 0.00 0.00 13.21800+8.752000i
#> 2 13.00430 8.388302 0.02 0.02 13.00430+8.388302i
#> 3 12.84269 7.962447 0.04 0.04 12.84269+7.962447i
#> 4 12.60229 7.553189 0.06 0.06 12.60229+7.553189i
#> 5 12.42317 7.169302 0.08 0.08 12.42317+7.169302i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_8 Sim_6 TrajSim_8_6
#> 2 -0.2137001-0.3636983i Traj_8 Sim_6 TrajSim_8_6
#> 3 -0.1616080-0.4258551i Traj_8 Sim_6 TrajSim_8_6
#> 4 -0.2403994-0.4092573i Traj_8 Sim_6 TrajSim_8_6
#> 5 -0.1791225-0.3838875i Traj_8 Sim_6 TrajSim_8_6
#>
#> [[6]][[9]]
#> x y time displacementTime polar
#> 1 15.63800 8.164000 0.00 0.00 15.63800+ 8.164000i
#> 2 15.28597 9.124702 0.02 0.02 15.28597+ 9.124702i
#> 3 14.99714 10.166010 0.04 0.04 14.99714+10.166010i
#> 4 14.57067 11.131589 0.06 0.06 14.57067+11.131589i
#> 5 14.14631 12.003943 0.08 0.08 14.14631+12.003943i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_9 Sim_6 TrajSim_9_6
#> 2 -0.3520340+0.9607015i Traj_9 Sim_6 TrajSim_9_6
#> 3 -0.2888253+1.0413081i Traj_9 Sim_6 TrajSim_9_6
#> 4 -0.4264735+0.9655789i Traj_9 Sim_6 TrajSim_9_6
#> 5 -0.4243596+0.8723543i Traj_9 Sim_6 TrajSim_9_6
#>
#> [[6]][[10]]
#> x y time displacementTime polar
#> 1 14.69800 6.798000 0.00 0.00 14.69800+ 6.798000i
#> 2 14.21498 7.558251 0.02 0.02 14.21498+ 7.558251i
#> 3 13.77950 8.247078 0.04 0.04 13.77950+ 8.247078i
#> 4 13.32947 8.968783 0.06 0.06 13.32947+ 8.968783i
#> 5 12.92799 9.808881 0.08 0.08 12.92799+ 9.808881i
#> 6 12.52050 10.615763 0.10 0.10 12.52050+10.615763i
#> 7 12.06790 11.389453 0.12 0.12 12.06790+11.389453i
#> 8 11.56957 12.129620 0.14 0.14 11.56957+12.129620i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_10 Sim_6 TrajSim_10_6
#> 2 -0.4830215+0.7602513i Traj_10 Sim_6 TrajSim_10_6
#> 3 -0.4354765+0.6888271i Traj_10 Sim_6 TrajSim_10_6
#> 4 -0.4500319+0.7217050i Traj_10 Sim_6 TrajSim_10_6
#> 5 -0.4014816+0.8400973i Traj_10 Sim_6 TrajSim_10_6
#> 6 -0.4074882+0.8068822i Traj_10 Sim_6 TrajSim_10_6
#> 7 -0.4525967+0.7736905i Traj_10 Sim_6 TrajSim_10_6
#> 8 -0.4983376+0.7401670i Traj_10 Sim_6 TrajSim_10_6
#>
#> [[6]][[11]]
#> x y time displacementTime polar
#> 1 12.00600 7.316000 0.00 0.00 12.00600+ 7.316000i
#> 2 11.65369 8.427778 0.02 0.02 11.65369+ 8.427778i
#> 3 11.36696 9.381321 0.04 0.04 11.36696+ 9.381321i
#> 4 11.03077 10.333844 0.06 0.06 11.03077+10.333844i
#> 5 10.65547 11.334495 0.08 0.08 10.65547+11.334495i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_11 Sim_6 TrajSim_11_6
#> 2 -0.3523126+1.1117781i Traj_11 Sim_6 TrajSim_11_6
#> 3 -0.2867289+0.9535424i Traj_11 Sim_6 TrajSim_11_6
#> 4 -0.3361848+0.9525238i Traj_11 Sim_6 TrajSim_11_6
#> 5 -0.3753031+1.0006503i Traj_11 Sim_6 TrajSim_11_6
#>
#>
#> [[7]]
#> [[7]][[1]]
#> x y time displacementTime polar
#> 1 36.88200 14.05600 0.00 0.00 36.88200+14.05600i
#> 2 36.24283 14.73887 0.02 0.02 36.24283+14.73887i
#> 3 35.64979 15.48800 0.04 0.04 35.64979+15.48800i
#> 4 34.96479 16.22785 0.06 0.06 34.96479+16.22785i
#> 5 34.40415 16.75646 0.08 0.08 34.40415+16.75646i
#> 6 33.71690 17.44266 0.10 0.10 33.71690+17.44266i
#> 7 32.95309 17.91655 0.12 0.12 32.95309+17.91655i
#> 8 32.15659 18.40205 0.14 0.14 32.15659+18.40205i
#> 9 31.40066 18.92729 0.16 0.16 31.40066+18.92729i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_1 Sim_7 TrajSim_1_7
#> 2 -0.6391749+0.6828747i Traj_1 Sim_7 TrajSim_1_7
#> 3 -0.5930384+0.7491204i Traj_1 Sim_7 TrajSim_1_7
#> 4 -0.6849957+0.7398527i Traj_1 Sim_7 TrajSim_1_7
#> 5 -0.5606372+0.5286140i Traj_1 Sim_7 TrajSim_1_7
#> 6 -0.6872510+0.6862032i Traj_1 Sim_7 TrajSim_1_7
#> 7 -0.7638156+0.4738864i Traj_1 Sim_7 TrajSim_1_7
#> 8 -0.7964946+0.4855009i Traj_1 Sim_7 TrajSim_1_7
#> 9 -0.7559301+0.5252386i Traj_1 Sim_7 TrajSim_1_7
#>
#> [[7]][[2]]
#> x y time displacementTime polar
#> 1 35.53200 13.51600 0.00 0.00 35.53200+13.51600i
#> 2 34.71033 14.27859 0.02 0.02 34.71033+14.27859i
#> 3 34.05215 14.85665 0.04 0.04 34.05215+14.85665i
#> 4 33.39432 15.48190 0.06 0.06 33.39432+15.48190i
#> 5 32.84173 16.26401 0.08 0.08 32.84173+16.26401i
#> 6 32.34297 17.31589 0.10 0.10 32.34297+17.31589i
#> 7 31.93691 18.13380 0.12 0.12 31.93691+18.13380i
#> 8 31.65331 19.14008 0.14 0.14 31.65331+19.14008i
#> 9 31.40238 20.05236 0.16 0.16 31.40238+20.05236i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_2 Sim_7 TrajSim_2_7
#> 2 -0.8216717+0.7625935i Traj_2 Sim_7 TrajSim_2_7
#> 3 -0.6581768+0.5780559i Traj_2 Sim_7 TrajSim_2_7
#> 4 -0.6578340+0.6252463i Traj_2 Sim_7 TrajSim_2_7
#> 5 -0.5525864+0.7821178i Traj_2 Sim_7 TrajSim_2_7
#> 6 -0.4987642+1.0518749i Traj_2 Sim_7 TrajSim_2_7
#> 7 -0.4060587+0.8179143i Traj_2 Sim_7 TrajSim_2_7
#> 8 -0.2836015+1.0062726i Traj_2 Sim_7 TrajSim_2_7
#> 9 -0.2509248+0.9122846i Traj_2 Sim_7 TrajSim_2_7
#>
#> [[7]][[3]]
#> x y time displacementTime polar
#> 1 34.54800 14.10000 0.00 0.00 34.54800+14.10000i
#> 2 33.66744 14.98666 0.02 0.02 33.66744+14.98666i
#> 3 32.82588 15.75807 0.04 0.04 32.82588+15.75807i
#> 4 31.74065 16.60227 0.06 0.06 31.74065+16.60227i
#> 5 31.00098 17.28143 0.08 0.08 31.00098+17.28143i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_3 Sim_7 TrajSim_3_7
#> 2 -0.8805580+0.8866573i Traj_3 Sim_7 TrajSim_3_7
#> 3 -0.8415619+0.7714130i Traj_3 Sim_7 TrajSim_3_7
#> 4 -1.0852282+0.8442023i Traj_3 Sim_7 TrajSim_3_7
#> 5 -0.7396753+0.6791547i Traj_3 Sim_7 TrajSim_3_7
#>
#> [[7]][[4]]
#> x y time displacementTime polar
#> 1 32.26000 14.51800 0.00 0.00 32.26000+14.51800i
#> 2 31.67478 15.31767 0.02 0.02 31.67478+15.31767i
#> 3 31.10309 16.04427 0.04 0.04 31.10309+16.04427i
#> 4 30.46558 16.80685 0.06 0.06 30.46558+16.80685i
#> 5 29.85352 17.58356 0.08 0.08 29.85352+17.58356i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_4 Sim_7 TrajSim_4_7
#> 2 -0.5852227+0.7996682i Traj_4 Sim_7 TrajSim_4_7
#> 3 -0.5716905+0.7265978i Traj_4 Sim_7 TrajSim_4_7
#> 4 -0.6375031+0.7625825i Traj_4 Sim_7 TrajSim_4_7
#> 5 -0.6120673+0.7767090i Traj_4 Sim_7 TrajSim_4_7
#>
#> [[7]][[5]]
#> x y time displacementTime polar
#> 1 28.29000 13.57800 0.00 0.00 28.29000+13.57800i
#> 2 27.93946 14.18286 0.02 0.02 27.93946+14.18286i
#> 3 27.37044 14.78723 0.04 0.04 27.37044+14.78723i
#> 4 26.95791 15.37632 0.06 0.06 26.95791+15.37632i
#> 5 26.44996 15.84576 0.08 0.08 26.44996+15.84576i
#> 6 25.60071 16.36765 0.10 0.10 25.60071+16.36765i
#> 7 24.81911 16.65188 0.12 0.12 24.81911+16.65188i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_5 Sim_7 TrajSim_5_7
#> 2 -0.3505403+0.6048644i Traj_5 Sim_7 TrajSim_5_7
#> 3 -0.5690155+0.6043651i Traj_5 Sim_7 TrajSim_5_7
#> 4 -0.4125378+0.5890925i Traj_5 Sim_7 TrajSim_5_7
#> 5 -0.5079462+0.4694359i Traj_5 Sim_7 TrajSim_5_7
#> 6 -0.8492512+0.5218886i Traj_5 Sim_7 TrajSim_5_7
#> 7 -0.7816020+0.2842350i Traj_5 Sim_7 TrajSim_5_7
#>
#> [[7]][[6]]
#> x y time displacementTime polar
#> 1 26.19800 13.69800 0.00 0.00 26.19800+13.69800i
#> 2 25.64595 14.63445 0.02 0.02 25.64595+14.63445i
#> 3 24.99705 15.61650 0.04 0.04 24.99705+15.61650i
#> 4 24.37504 16.47129 0.06 0.06 24.37504+16.47129i
#> 5 23.63417 17.25977 0.08 0.08 23.63417+17.25977i
#> 6 22.76234 18.01859 0.10 0.10 22.76234+18.01859i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_6 Sim_7 TrajSim_6_7
#> 2 -0.5520500+0.9364490i Traj_6 Sim_7 TrajSim_6_7
#> 3 -0.6489045+0.9820483i Traj_6 Sim_7 TrajSim_6_7
#> 4 -0.6220098+0.8547951i Traj_6 Sim_7 TrajSim_6_7
#> 5 -0.7408639+0.7884785i Traj_6 Sim_7 TrajSim_6_7
#> 6 -0.8718300+0.7588181i Traj_6 Sim_7 TrajSim_6_7
#>
#> [[7]][[7]]
#> x y time displacementTime polar
#> 1 26.47200 15.49600 0.00 0.00 26.47200+15.49600i
#> 2 27.34960 15.10569 0.02 0.02 27.34960+15.10569i
#> 3 28.41832 14.60831 0.04 0.04 28.41832+14.60831i
#> 4 29.43166 14.15290 0.06 0.06 29.43166+14.15290i
#> 5 30.47011 13.68507 0.08 0.08 30.47011+13.68507i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_7 Sim_7 TrajSim_7_7
#> 2 0.8775959-0.3903123i Traj_7 Sim_7 TrajSim_7_7
#> 3 1.0687218-0.4973793i Traj_7 Sim_7 TrajSim_7_7
#> 4 1.0133425-0.4554097i Traj_7 Sim_7 TrajSim_7_7
#> 5 1.0384520-0.4678326i Traj_7 Sim_7 TrajSim_7_7
#>
#> [[7]][[8]]
#> x y time displacementTime polar
#> 1 13.21800 8.752000 0.00 0.00 13.21800+8.752000i
#> 2 12.91831 8.516993 0.02 0.02 12.91831+8.516993i
#> 3 12.60025 8.292168 0.04 0.04 12.60025+8.292168i
#> 4 12.28650 8.025915 0.06 0.06 12.28650+8.025915i
#> 5 11.90691 7.842248 0.08 0.08 11.90691+7.842248i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_8 Sim_7 TrajSim_8_7
#> 2 -0.2996936-0.2350071i Traj_8 Sim_7 TrajSim_8_7
#> 3 -0.3180556-0.2248251i Traj_8 Sim_7 TrajSim_8_7
#> 4 -0.3137540-0.2662532i Traj_8 Sim_7 TrajSim_8_7
#> 5 -0.3795864-0.1836666i Traj_8 Sim_7 TrajSim_8_7
#>
#> [[7]][[9]]
#> x y time displacementTime polar
#> 1 15.63800 8.164000 0.00 0.00 15.63800+ 8.164000i
#> 2 15.28226 9.169693 0.02 0.02 15.28226+ 9.169693i
#> 3 14.83689 10.123582 0.04 0.04 14.83689+10.123582i
#> 4 14.46161 11.132483 0.06 0.06 14.46161+11.132483i
#> 5 13.98832 11.989449 0.08 0.08 13.98832+11.989449i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_9 Sim_7 TrajSim_9_7
#> 2 -0.3557408+1.0056931i Traj_9 Sim_7 TrajSim_9_7
#> 3 -0.4453657+0.9538887i Traj_9 Sim_7 TrajSim_9_7
#> 4 -0.3752856+1.0089014i Traj_9 Sim_7 TrajSim_9_7
#> 5 -0.4732858+0.8569654i Traj_9 Sim_7 TrajSim_9_7
#>
#> [[7]][[10]]
#> x y time displacementTime polar
#> 1 14.69800 6.798000 0.00 0.00 14.69800+ 6.798000i
#> 2 14.15031 7.488072 0.02 0.02 14.15031+ 7.488072i
#> 3 13.62407 8.173715 0.04 0.04 13.62407+ 8.173715i
#> 4 13.13813 8.895695 0.06 0.06 13.13813+ 8.895695i
#> 5 12.52693 9.620935 0.08 0.08 12.52693+ 9.620935i
#> 6 11.95231 10.395372 0.10 0.10 11.95231+10.395372i
#> 7 11.46804 11.074244 0.12 0.12 11.46804+11.074244i
#> 8 10.91179 11.844391 0.14 0.14 10.91179+11.844391i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_10 Sim_7 TrajSim_10_7
#> 2 -0.5476940+0.6900718i Traj_10 Sim_7 TrajSim_10_7
#> 3 -0.5262334+0.6856433i Traj_10 Sim_7 TrajSim_10_7
#> 4 -0.4859384+0.7219795i Traj_10 Sim_7 TrajSim_10_7
#> 5 -0.6112015+0.7252405i Traj_10 Sim_7 TrajSim_10_7
#> 6 -0.5746182+0.7744365i Traj_10 Sim_7 TrajSim_10_7
#> 7 -0.4842781+0.6788719i Traj_10 Sim_7 TrajSim_10_7
#> 8 -0.5562510+0.7701476i Traj_10 Sim_7 TrajSim_10_7
#>
#> [[7]][[11]]
#> x y time displacementTime polar
#> 1 12.00600 7.316000 0.00 0.00 12.00600+ 7.316000i
#> 2 11.62995 8.254431 0.02 0.02 11.62995+ 8.254431i
#> 3 11.14568 9.250607 0.04 0.04 11.14568+ 9.250607i
#> 4 10.68043 10.114592 0.06 0.06 10.68043+10.114592i
#> 5 10.14751 11.015540 0.08 0.08 10.14751+11.015540i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_11 Sim_7 TrajSim_11_7
#> 2 -0.3760461+0.9384312i Traj_11 Sim_7 TrajSim_11_7
#> 3 -0.4842691+0.9961758i Traj_11 Sim_7 TrajSim_11_7
#> 4 -0.4652593+0.8639846i Traj_11 Sim_7 TrajSim_11_7
#> 5 -0.5329106+0.9009483i Traj_11 Sim_7 TrajSim_11_7
#>
#>
#> [[8]]
#> [[8]][[1]]
#> x y time displacementTime polar
#> 1 36.88200 14.05600 0.00 0.00 36.88200+14.05600i
#> 2 36.18238 14.52256 0.02 0.02 36.18238+14.52256i
#> 3 35.45337 15.02457 0.04 0.04 35.45337+15.02457i
#> 4 34.68105 15.51696 0.06 0.06 34.68105+15.51696i
#> 5 34.08772 15.98008 0.08 0.08 34.08772+15.98008i
#> 6 33.46948 16.65255 0.10 0.10 33.46948+16.65255i
#> 7 32.85426 17.39518 0.12 0.12 32.85426+17.39518i
#> 8 32.30207 17.98654 0.14 0.14 32.30207+17.98654i
#> 9 31.80023 18.59330 0.16 0.16 31.80023+18.59330i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_1 Sim_8 TrajSim_1_8
#> 2 -0.6996237+0.4665601i Traj_1 Sim_8 TrajSim_1_8
#> 3 -0.7290022+0.5020102i Traj_1 Sim_8 TrajSim_1_8
#> 4 -0.7723209+0.4923898i Traj_1 Sim_8 TrajSim_1_8
#> 5 -0.5933354+0.4631170i Traj_1 Sim_8 TrajSim_1_8
#> 6 -0.6182337+0.6724764i Traj_1 Sim_8 TrajSim_1_8
#> 7 -0.6152256+0.7426287i Traj_1 Sim_8 TrajSim_1_8
#> 8 -0.5521885+0.5913582i Traj_1 Sim_8 TrajSim_1_8
#> 9 -0.5018390+0.6067606i Traj_1 Sim_8 TrajSim_1_8
#>
#> [[8]][[2]]
#> x y time displacementTime polar
#> 1 35.53200 13.51600 0.00 0.00 35.53200+13.51600i
#> 2 34.96194 14.18884 0.02 0.02 34.96194+14.18884i
#> 3 34.40982 14.97430 0.04 0.04 34.40982+14.97430i
#> 4 33.73040 15.73051 0.06 0.06 33.73040+15.73051i
#> 5 33.00529 16.44880 0.08 0.08 33.00529+16.44880i
#> 6 32.15069 17.15292 0.10 0.10 32.15069+17.15292i
#> 7 31.34136 17.71612 0.12 0.12 31.34136+17.71612i
#> 8 30.55152 18.18794 0.14 0.14 30.55152+18.18794i
#> 9 29.74839 18.58194 0.16 0.16 29.74839+18.58194i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_2 Sim_8 TrajSim_2_8
#> 2 -0.5700595+0.6728418i Traj_2 Sim_8 TrajSim_2_8
#> 3 -0.5521157+0.7854552i Traj_2 Sim_8 TrajSim_2_8
#> 4 -0.6794296+0.7562125i Traj_2 Sim_8 TrajSim_2_8
#> 5 -0.7251034+0.7182933i Traj_2 Sim_8 TrajSim_2_8
#> 6 -0.8545998+0.7041147i Traj_2 Sim_8 TrajSim_2_8
#> 7 -0.8093275+0.5632001i Traj_2 Sim_8 TrajSim_2_8
#> 8 -0.7898488+0.4718198i Traj_2 Sim_8 TrajSim_2_8
#> 9 -0.8031259+0.3940050i Traj_2 Sim_8 TrajSim_2_8
#>
#> [[8]][[3]]
#> x y time displacementTime polar
#> 1 34.54800 14.10000 0.00 0.00 34.54800+14.10000i
#> 2 33.74589 14.85041 0.02 0.02 33.74589+14.85041i
#> 3 32.85923 15.51301 0.04 0.04 32.85923+15.51301i
#> 4 31.88504 16.23706 0.06 0.06 31.88504+16.23706i
#> 5 31.01203 16.86988 0.08 0.08 31.01203+16.86988i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_3 Sim_8 TrajSim_3_8
#> 2 -0.8021115+0.7504101i Traj_3 Sim_8 TrajSim_3_8
#> 3 -0.8866586+0.6625962i Traj_3 Sim_8 TrajSim_3_8
#> 4 -0.9741859+0.7240492i Traj_3 Sim_8 TrajSim_3_8
#> 5 -0.8730189+0.6328283i Traj_3 Sim_8 TrajSim_3_8
#>
#> [[8]][[4]]
#> x y time displacementTime polar
#> 1 32.26000 14.51800 0.00 0.00 32.26000+14.51800i
#> 2 31.76174 15.41429 0.02 0.02 31.76174+15.41429i
#> 3 31.22618 16.37944 0.04 0.04 31.22618+16.37944i
#> 4 30.68672 17.27398 0.06 0.06 30.68672+17.27398i
#> 5 30.15606 18.05165 0.08 0.08 30.15606+18.05165i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_4 Sim_8 TrajSim_4_8
#> 2 -0.4982626+0.8962900i Traj_4 Sim_8 TrajSim_4_8
#> 3 -0.5355606+0.9651470i Traj_4 Sim_8 TrajSim_4_8
#> 4 -0.5394560+0.8945442i Traj_4 Sim_8 TrajSim_4_8
#> 5 -0.5306575+0.7776663i Traj_4 Sim_8 TrajSim_4_8
#>
#> [[8]][[5]]
#> x y time displacementTime polar
#> 1 28.29000 13.57800 0.00 0.00 28.29000+13.57800i
#> 2 27.90725 14.27862 0.02 0.02 27.90725+14.27862i
#> 3 27.63122 15.01512 0.04 0.04 27.63122+15.01512i
#> 4 27.40112 15.77308 0.06 0.06 27.40112+15.77308i
#> 5 27.23513 16.52880 0.08 0.08 27.23513+16.52880i
#> 6 27.02040 17.36967 0.10 0.10 27.02040+17.36967i
#> 7 26.99619 18.07981 0.12 0.12 26.99619+18.07981i
#> displacement Trajectory Simulation TrajSim
#> 1 0.00000000+0.0000000i Traj_5 Sim_8 TrajSim_5_8
#> 2 -0.38275304+0.7006195i Traj_5 Sim_8 TrajSim_5_8
#> 3 -0.27602802+0.7365031i Traj_5 Sim_8 TrajSim_5_8
#> 4 -0.23010312+0.7579548i Traj_5 Sim_8 TrajSim_5_8
#> 5 -0.16598532+0.7557245i Traj_5 Sim_8 TrajSim_5_8
#> 6 -0.21473180+0.8408692i Traj_5 Sim_8 TrajSim_5_8
#> 7 -0.02421043+0.7101394i Traj_5 Sim_8 TrajSim_5_8
#>
#> [[8]][[6]]
#> x y time displacementTime polar
#> 1 26.19800 13.69800 0.00 0.00 26.19800+13.69800i
#> 2 25.65766 14.59359 0.02 0.02 25.65766+14.59359i
#> 3 25.02451 15.49893 0.04 0.04 25.02451+15.49893i
#> 4 24.36447 16.14105 0.06 0.06 24.36447+16.14105i
#> 5 23.68725 16.92297 0.08 0.08 23.68725+16.92297i
#> 6 22.96466 17.62504 0.10 0.10 22.96466+17.62504i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_6 Sim_8 TrajSim_6_8
#> 2 -0.5403436+0.8955893i Traj_6 Sim_8 TrajSim_6_8
#> 3 -0.6331453+0.9053449i Traj_6 Sim_8 TrajSim_6_8
#> 4 -0.6600418+0.6421171i Traj_6 Sim_8 TrajSim_6_8
#> 5 -0.6772161+0.7819234i Traj_6 Sim_8 TrajSim_6_8
#> 6 -0.7225888+0.7020673i Traj_6 Sim_8 TrajSim_6_8
#>
#> [[8]][[7]]
#> x y time displacementTime polar
#> 1 26.47200 15.49600 0.00 0.00 26.47200+15.49600i
#> 2 27.63894 14.96444 0.02 0.02 27.63894+14.96444i
#> 3 28.56495 14.51934 0.04 0.04 28.56495+14.51934i
#> 4 29.55401 13.94101 0.06 0.06 29.55401+13.94101i
#> 5 30.77842 13.29632 0.08 0.08 30.77842+13.29632i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_7 Sim_8 TrajSim_7_8
#> 2 1.1669415-0.5315554i Traj_7 Sim_8 TrajSim_7_8
#> 3 0.9260069-0.4451042i Traj_7 Sim_8 TrajSim_7_8
#> 4 0.9890578-0.5783300i Traj_7 Sim_8 TrajSim_7_8
#> 5 1.2244175-0.6446875i Traj_7 Sim_8 TrajSim_7_8
#>
#> [[8]][[8]]
#> x y time displacementTime polar
#> 1 13.21800 8.752000 0.00 0.00 13.21800+8.752000i
#> 2 12.90008 8.495625 0.02 0.02 12.90008+8.495625i
#> 3 12.70119 8.110504 0.04 0.04 12.70119+8.110504i
#> 4 12.44513 7.838397 0.06 0.06 12.44513+7.838397i
#> 5 12.14762 7.510670 0.08 0.08 12.14762+7.510670i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_8 Sim_8 TrajSim_8_8
#> 2 -0.3179248-0.2563746i Traj_8 Sim_8 TrajSim_8_8
#> 3 -0.1988841-0.3851212i Traj_8 Sim_8 TrajSim_8_8
#> 4 -0.2560639-0.2721074i Traj_8 Sim_8 TrajSim_8_8
#> 5 -0.2975050-0.3277272i Traj_8 Sim_8 TrajSim_8_8
#>
#> [[8]][[9]]
#> x y time displacementTime polar
#> 1 15.63800 8.16400 0.00 0.00 15.63800+ 8.16400i
#> 2 15.34409 9.21531 0.02 0.02 15.34409+ 9.21531i
#> 3 15.11253 10.12242 0.04 0.04 15.11253+10.12242i
#> 4 14.74796 11.11808 0.06 0.06 14.74796+11.11808i
#> 5 14.39065 12.08639 0.08 0.08 14.39065+12.08639i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_9 Sim_8 TrajSim_9_8
#> 2 -0.2939121+1.0513104i Traj_9 Sim_8 TrajSim_9_8
#> 3 -0.2315578+0.9071102i Traj_9 Sim_8 TrajSim_9_8
#> 4 -0.3645691+0.9956552i Traj_9 Sim_8 TrajSim_9_8
#> 5 -0.3573127+0.9683106i Traj_9 Sim_8 TrajSim_9_8
#>
#> [[8]][[10]]
#> x y time displacementTime polar
#> 1 14.69800 6.798000 0.00 0.00 14.69800+ 6.798000i
#> 2 14.05637 7.594147 0.02 0.02 14.05637+ 7.594147i
#> 3 13.52461 8.374802 0.04 0.04 13.52461+ 8.374802i
#> 4 13.00554 9.172719 0.06 0.06 13.00554+ 9.172719i
#> 5 12.43654 9.835022 0.08 0.08 12.43654+ 9.835022i
#> 6 11.86434 10.490402 0.10 0.10 11.86434+10.490402i
#> 7 11.27261 11.134935 0.12 0.12 11.27261+11.134935i
#> 8 10.57988 11.872553 0.14 0.14 10.57988+11.872553i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_10 Sim_8 TrajSim_10_8
#> 2 -0.6416343+0.7961469i Traj_10 Sim_8 TrajSim_10_8
#> 3 -0.5317550+0.7806550i Traj_10 Sim_8 TrajSim_10_8
#> 4 -0.5190670+0.7979172i Traj_10 Sim_8 TrajSim_10_8
#> 5 -0.5690066+0.6623026i Traj_10 Sim_8 TrajSim_10_8
#> 6 -0.5721996+0.6553801i Traj_10 Sim_8 TrajSim_10_8
#> 7 -0.5917291+0.6445335i Traj_10 Sim_8 TrajSim_10_8
#> 8 -0.6927245+0.7376182i Traj_10 Sim_8 TrajSim_10_8
#>
#> [[8]][[11]]
#> x y time displacementTime polar
#> 1 12.00600 7.316000 0.00 0.00 12.00600+ 7.316000i
#> 2 11.65672 8.289461 0.02 0.02 11.65672+ 8.289461i
#> 3 11.36235 9.368277 0.04 0.04 11.36235+ 9.368277i
#> 4 11.02568 10.553081 0.06 0.06 11.02568+10.553081i
#> 5 10.75117 11.613467 0.08 0.08 10.75117+11.613467i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_11 Sim_8 TrajSim_11_8
#> 2 -0.3492790+0.9734607i Traj_11 Sim_8 TrajSim_11_8
#> 3 -0.2943722+1.0788166i Traj_11 Sim_8 TrajSim_11_8
#> 4 -0.3366645+1.1848037i Traj_11 Sim_8 TrajSim_11_8
#> 5 -0.2745179+1.0603857i Traj_11 Sim_8 TrajSim_11_8
#>
#>
#> [[9]]
#> [[9]][[1]]
#> x y time displacementTime polar
#> 1 36.88200 14.05600 0.00 0.00 36.88200+14.05600i
#> 2 36.13666 14.72731 0.02 0.02 36.13666+14.72731i
#> 3 35.47906 15.17759 0.04 0.04 35.47906+15.17759i
#> 4 34.73670 15.63562 0.06 0.06 34.73670+15.63562i
#> 5 33.95975 16.18250 0.08 0.08 33.95975+16.18250i
#> 6 33.25510 16.72740 0.10 0.10 33.25510+16.72740i
#> 7 32.55175 17.17479 0.12 0.12 32.55175+17.17479i
#> 8 31.87075 17.81797 0.14 0.14 31.87075+17.81797i
#> 9 31.20488 18.36246 0.16 0.16 31.20488+18.36246i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_1 Sim_9 TrajSim_1_9
#> 2 -0.7453364+0.6713075i Traj_1 Sim_9 TrajSim_1_9
#> 3 -0.6576039+0.4502823i Traj_1 Sim_9 TrajSim_1_9
#> 4 -0.7423575+0.4580261i Traj_1 Sim_9 TrajSim_1_9
#> 5 -0.7769546+0.5468824i Traj_1 Sim_9 TrajSim_1_9
#> 6 -0.7046460+0.5448986i Traj_1 Sim_9 TrajSim_1_9
#> 7 -0.7033515+0.4473923i Traj_1 Sim_9 TrajSim_1_9
#> 8 -0.6809963+0.6431815i Traj_1 Sim_9 TrajSim_1_9
#> 9 -0.6658695+0.5444937i Traj_1 Sim_9 TrajSim_1_9
#>
#> [[9]][[2]]
#> x y time displacementTime polar
#> 1 35.53200 13.51600 0.00 0.00 35.53200+13.51600i
#> 2 35.14201 14.13095 0.02 0.02 35.14201+14.13095i
#> 3 34.59500 14.96538 0.04 0.04 34.59500+14.96538i
#> 4 33.93774 15.69042 0.06 0.06 33.93774+15.69042i
#> 5 33.29537 16.39898 0.08 0.08 33.29537+16.39898i
#> 6 32.56256 17.08197 0.10 0.10 32.56256+17.08197i
#> 7 31.88716 17.58259 0.12 0.12 31.88716+17.58259i
#> 8 31.17890 18.07006 0.14 0.14 31.17890+18.07006i
#> 9 30.35973 18.57289 0.16 0.16 30.35973+18.57289i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_2 Sim_9 TrajSim_2_9
#> 2 -0.3899911+0.6149481i Traj_2 Sim_9 TrajSim_2_9
#> 3 -0.5470058+0.8344302i Traj_2 Sim_9 TrajSim_2_9
#> 4 -0.6572588+0.7250396i Traj_2 Sim_9 TrajSim_2_9
#> 5 -0.6423710+0.7085660i Traj_2 Sim_9 TrajSim_2_9
#> 6 -0.7328167+0.6829887i Traj_2 Sim_9 TrajSim_2_9
#> 7 -0.6754001+0.5006214i Traj_2 Sim_9 TrajSim_2_9
#> 8 -0.7082517+0.4874628i Traj_2 Sim_9 TrajSim_2_9
#> 9 -0.8191716+0.5028365i Traj_2 Sim_9 TrajSim_2_9
#>
#> [[9]][[3]]
#> x y time displacementTime polar
#> 1 34.54800 14.10000 0.00 0.00 34.54800+14.10000i
#> 2 33.64949 14.85754 0.02 0.02 33.64949+14.85754i
#> 3 32.79869 15.53972 0.04 0.04 32.79869+15.53972i
#> 4 31.84547 16.23302 0.06 0.06 31.84547+16.23302i
#> 5 30.96742 16.83215 0.08 0.08 30.96742+16.83215i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_3 Sim_9 TrajSim_3_9
#> 2 -0.8985098+0.7575431i Traj_3 Sim_9 TrajSim_3_9
#> 3 -0.8507985+0.6821740i Traj_3 Sim_9 TrajSim_3_9
#> 4 -0.9532226+0.6933021i Traj_3 Sim_9 TrajSim_3_9
#> 5 -0.8780521+0.5991304i Traj_3 Sim_9 TrajSim_3_9
#>
#> [[9]][[4]]
#> x y time displacementTime polar
#> 1 32.26000 14.51800 0.00 0.00 32.26000+14.51800i
#> 2 31.76839 15.28432 0.02 0.02 31.76839+15.28432i
#> 3 31.29390 16.12625 0.04 0.04 31.29390+16.12625i
#> 4 30.84892 17.05858 0.06 0.06 30.84892+17.05858i
#> 5 30.29460 18.05124 0.08 0.08 30.29460+18.05124i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_4 Sim_9 TrajSim_4_9
#> 2 -0.4916118+0.7663179i Traj_4 Sim_9 TrajSim_4_9
#> 3 -0.4744905+0.8419301i Traj_4 Sim_9 TrajSim_4_9
#> 4 -0.4449776+0.9323363i Traj_4 Sim_9 TrajSim_4_9
#> 5 -0.5543153+0.9926576i Traj_4 Sim_9 TrajSim_4_9
#>
#> [[9]][[5]]
#> x y time displacementTime polar
#> 1 28.29000 13.57800 0.00 0.00 28.29000+13.57800i
#> 2 28.05342 14.25315 0.02 0.02 28.05342+14.25315i
#> 3 27.76428 14.94731 0.04 0.04 27.76428+14.94731i
#> 4 27.50423 15.64005 0.06 0.06 27.50423+15.64005i
#> 5 27.22528 16.49181 0.08 0.08 27.22528+16.49181i
#> 6 26.95411 17.27260 0.10 0.10 26.95411+17.27260i
#> 7 26.53355 18.05933 0.12 0.12 26.53355+18.05933i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_5 Sim_9 TrajSim_5_9
#> 2 -0.2365765+0.6751495i Traj_5 Sim_9 TrajSim_5_9
#> 3 -0.2891459+0.6941624i Traj_5 Sim_9 TrajSim_5_9
#> 4 -0.2600512+0.6927393i Traj_5 Sim_9 TrajSim_5_9
#> 5 -0.2789442+0.8517581i Traj_5 Sim_9 TrajSim_5_9
#> 6 -0.2711673+0.7807889i Traj_5 Sim_9 TrajSim_5_9
#> 7 -0.4205665+0.7867322i Traj_5 Sim_9 TrajSim_5_9
#>
#> [[9]][[6]]
#> x y time displacementTime polar
#> 1 26.19800 13.69800 0.00 0.00 26.19800+13.69800i
#> 2 25.54200 14.47383 0.02 0.02 25.54200+14.47383i
#> 3 24.96338 15.16092 0.04 0.04 24.96338+15.16092i
#> 4 24.19227 16.03463 0.06 0.06 24.19227+16.03463i
#> 5 23.39715 16.85142 0.08 0.08 23.39715+16.85142i
#> 6 22.65165 17.52497 0.10 0.10 22.65165+17.52497i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_6 Sim_9 TrajSim_6_9
#> 2 -0.6559969+0.7758296i Traj_6 Sim_9 TrajSim_6_9
#> 3 -0.5786204+0.6870910i Traj_6 Sim_9 TrajSim_6_9
#> 4 -0.7711122+0.8737067i Traj_6 Sim_9 TrajSim_6_9
#> 5 -0.7951158+0.8167879i Traj_6 Sim_9 TrajSim_6_9
#> 6 -0.7455046+0.6735519i Traj_6 Sim_9 TrajSim_6_9
#>
#> [[9]][[7]]
#> x y time displacementTime polar
#> 1 26.47200 15.49600 0.00 0.00 26.47200+15.49600i
#> 2 27.60477 15.08961 0.02 0.02 27.60477+15.08961i
#> 3 28.81759 14.65588 0.04 0.04 28.81759+14.65588i
#> 4 30.01135 14.19824 0.06 0.06 30.01135+14.19824i
#> 5 30.99458 13.83726 0.08 0.08 30.99458+13.83726i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_7 Sim_9 TrajSim_7_9
#> 2 1.1327720-0.4063922i Traj_7 Sim_9 TrajSim_7_9
#> 3 1.2128214-0.4337269i Traj_7 Sim_9 TrajSim_7_9
#> 4 1.1937597-0.4576422i Traj_7 Sim_9 TrajSim_7_9
#> 5 0.9832282-0.3609788i Traj_7 Sim_9 TrajSim_7_9
#>
#> [[9]][[8]]
#> x y time displacementTime polar
#> 1 13.21800 8.752000 0.00 0.00 13.21800+8.752000i
#> 2 13.04153 8.368473 0.02 0.02 13.04153+8.368473i
#> 3 12.86876 8.005217 0.04 0.04 12.86876+8.005217i
#> 4 12.67483 7.627727 0.06 0.06 12.67483+7.627727i
#> 5 12.37153 7.295370 0.08 0.08 12.37153+7.295370i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_8 Sim_9 TrajSim_8_9
#> 2 -0.1764658-0.3835272i Traj_8 Sim_9 TrajSim_8_9
#> 3 -0.1727698-0.3632561i Traj_8 Sim_9 TrajSim_8_9
#> 4 -0.1939391-0.3774898i Traj_8 Sim_9 TrajSim_8_9
#> 5 -0.3032935-0.3323566i Traj_8 Sim_9 TrajSim_8_9
#>
#> [[9]][[9]]
#> x y time displacementTime polar
#> 1 15.63800 8.164000 0.00 0.00 15.63800+ 8.164000i
#> 2 15.21165 9.091647 0.02 0.02 15.21165+ 9.091647i
#> 3 14.94248 10.070800 0.04 0.04 14.94248+10.070800i
#> 4 14.70624 11.092421 0.06 0.06 14.70624+11.092421i
#> 5 14.46788 12.212002 0.08 0.08 14.46788+12.212002i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_9 Sim_9 TrajSim_9_9
#> 2 -0.4263545+0.9276475i Traj_9 Sim_9 TrajSim_9_9
#> 3 -0.2691665+0.9791525i Traj_9 Sim_9 TrajSim_9_9
#> 4 -0.2362432+1.0216211i Traj_9 Sim_9 TrajSim_9_9
#> 5 -0.2383604+1.1195812i Traj_9 Sim_9 TrajSim_9_9
#>
#> [[9]][[10]]
#> x y time displacementTime polar
#> 1 14.69800 6.798000 0.00 0.00 14.69800+ 6.798000i
#> 2 14.17064 7.563308 0.02 0.02 14.17064+ 7.563308i
#> 3 13.60337 8.423738 0.04 0.04 13.60337+ 8.423738i
#> 4 13.00962 9.205885 0.06 0.06 13.00962+ 9.205885i
#> 5 12.41977 9.948970 0.08 0.08 12.41977+ 9.948970i
#> 6 11.88854 10.706973 0.10 0.10 11.88854+10.706973i
#> 7 11.33974 11.560450 0.12 0.12 11.33974+11.560450i
#> 8 10.73859 12.266667 0.14 0.14 10.73859+12.266667i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_10 Sim_9 TrajSim_10_9
#> 2 -0.5273605+0.7653076i Traj_10 Sim_9 TrajSim_10_9
#> 3 -0.5672725+0.8604305i Traj_10 Sim_9 TrajSim_10_9
#> 4 -0.5937512+0.7821467i Traj_10 Sim_9 TrajSim_10_9
#> 5 -0.5898443+0.7430851i Traj_10 Sim_9 TrajSim_10_9
#> 6 -0.5312273+0.7580033i Traj_10 Sim_9 TrajSim_10_9
#> 7 -0.5487997+0.8534770i Traj_10 Sim_9 TrajSim_10_9
#> 8 -0.6011497+0.7062166i Traj_10 Sim_9 TrajSim_10_9
#>
#> [[9]][[11]]
#> x y time displacementTime polar
#> 1 12.00600 7.316000 0.00 0.00 12.00600+ 7.316000i
#> 2 11.56347 8.431770 0.02 0.02 11.56347+ 8.431770i
#> 3 11.18610 9.334409 0.04 0.04 11.18610+ 9.334409i
#> 4 10.67688 10.271237 0.06 0.06 10.67688+10.271237i
#> 5 10.17386 11.230785 0.08 0.08 10.17386+11.230785i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_11 Sim_9 TrajSim_11_9
#> 2 -0.4425342+1.1157703i Traj_11 Sim_9 TrajSim_11_9
#> 3 -0.3773702+0.9026391i Traj_11 Sim_9 TrajSim_11_9
#> 4 -0.5092184+0.9368276i Traj_11 Sim_9 TrajSim_11_9
#> 5 -0.5030136+0.9595484i Traj_11 Sim_9 TrajSim_11_9
#>
#>
#> [[10]]
#> [[10]][[1]]
#> x y time displacementTime polar
#> 1 36.88200 14.05600 0.00 0.00 36.88200+14.05600i
#> 2 36.09288 14.53935 0.02 0.02 36.09288+14.53935i
#> 3 35.49103 15.14199 0.04 0.04 35.49103+15.14199i
#> 4 34.86827 15.87515 0.06 0.06 34.86827+15.87515i
#> 5 34.22633 16.37292 0.08 0.08 34.22633+16.37292i
#> 6 33.52331 16.99975 0.10 0.10 33.52331+16.99975i
#> 7 32.91045 17.57703 0.12 0.12 32.91045+17.57703i
#> 8 32.23988 18.16994 0.14 0.14 32.23988+18.16994i
#> 9 31.67142 18.73370 0.16 0.16 31.67142+18.73370i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_1 Sim_10 TrajSim_1_10
#> 2 -0.7891179+0.4833542i Traj_1 Sim_10 TrajSim_1_10
#> 3 -0.6018472+0.6026348i Traj_1 Sim_10 TrajSim_1_10
#> 4 -0.6227608+0.7331648i Traj_1 Sim_10 TrajSim_1_10
#> 5 -0.6419403+0.4977634i Traj_1 Sim_10 TrajSim_1_10
#> 6 -0.7030289+0.6268314i Traj_1 Sim_10 TrajSim_1_10
#> 7 -0.6128564+0.5772841i Traj_1 Sim_10 TrajSim_1_10
#> 8 -0.6705674+0.5929093i Traj_1 Sim_10 TrajSim_1_10
#> 9 -0.5684611+0.5637567i Traj_1 Sim_10 TrajSim_1_10
#>
#> [[10]][[2]]
#> x y time displacementTime polar
#> 1 35.53200 13.51600 0.00 0.00 35.53200+13.51600i
#> 2 34.84675 14.10344 0.02 0.02 34.84675+14.10344i
#> 3 34.12633 14.79742 0.04 0.04 34.12633+14.79742i
#> 4 33.35377 15.44286 0.06 0.06 33.35377+15.44286i
#> 5 32.63475 16.08870 0.08 0.08 32.63475+16.08870i
#> 6 31.78581 16.71140 0.10 0.10 31.78581+16.71140i
#> 7 31.09874 17.29225 0.12 0.12 31.09874+17.29225i
#> 8 30.39790 17.85426 0.14 0.14 30.39790+17.85426i
#> 9 29.71171 18.56574 0.16 0.16 29.71171+18.56574i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_2 Sim_10 TrajSim_2_10
#> 2 -0.6852527+0.5874374i Traj_2 Sim_10 TrajSim_2_10
#> 3 -0.7204165+0.6939814i Traj_2 Sim_10 TrajSim_2_10
#> 4 -0.7725604+0.6454396i Traj_2 Sim_10 TrajSim_2_10
#> 5 -0.7190204+0.6458374i Traj_2 Sim_10 TrajSim_2_10
#> 6 -0.8489405+0.6227082i Traj_2 Sim_10 TrajSim_2_10
#> 7 -0.6870662+0.5808444i Traj_2 Sim_10 TrajSim_2_10
#> 8 -0.7008419+0.5620109i Traj_2 Sim_10 TrajSim_2_10
#> 9 -0.6861949+0.7114805i Traj_2 Sim_10 TrajSim_2_10
#>
#> [[10]][[3]]
#> x y time displacementTime polar
#> 1 34.54800 14.10000 0.00 0.00 34.54800+14.10000i
#> 2 33.77976 14.87121 0.02 0.02 33.77976+14.87121i
#> 3 33.05566 15.76211 0.04 0.04 33.05566+15.76211i
#> 4 32.36946 16.64333 0.06 0.06 32.36946+16.64333i
#> 5 31.56426 17.53404 0.08 0.08 31.56426+17.53404i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_3 Sim_10 TrajSim_3_10
#> 2 -0.7682435+0.7712059i Traj_3 Sim_10 TrajSim_3_10
#> 3 -0.7240963+0.8909010i Traj_3 Sim_10 TrajSim_3_10
#> 4 -0.6862030+0.8812239i Traj_3 Sim_10 TrajSim_3_10
#> 5 -0.8052020+0.8907115i Traj_3 Sim_10 TrajSim_3_10
#>
#> [[10]][[4]]
#> x y time displacementTime polar
#> 1 32.26000 14.51800 0.00 0.00 32.26000+14.51800i
#> 2 31.58047 15.06138 0.02 0.02 31.58047+15.06138i
#> 3 30.71753 15.60820 0.04 0.04 30.71753+15.60820i
#> 4 29.93677 16.20145 0.06 0.06 29.93677+16.20145i
#> 5 29.20354 16.94732 0.08 0.08 29.20354+16.94732i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_4 Sim_10 TrajSim_4_10
#> 2 -0.6795340+0.5433847i Traj_4 Sim_10 TrajSim_4_10
#> 3 -0.8629349+0.5468171i Traj_4 Sim_10 TrajSim_4_10
#> 4 -0.7807609+0.5932501i Traj_4 Sim_10 TrajSim_4_10
#> 5 -0.7332284+0.7458643i Traj_4 Sim_10 TrajSim_4_10
#>
#> [[10]][[5]]
#> x y time displacementTime polar
#> 1 28.29000 13.57800 0.00 0.00 28.29000+13.57800i
#> 2 27.89063 14.27007 0.02 0.02 27.89063+14.27007i
#> 3 27.68187 15.11877 0.04 0.04 27.68187+15.11877i
#> 4 27.39416 15.83986 0.06 0.06 27.39416+15.83986i
#> 5 27.12861 16.47165 0.08 0.08 27.12861+16.47165i
#> 6 26.71858 17.28372 0.10 0.10 26.71858+17.28372i
#> 7 26.29904 18.12154 0.12 0.12 26.29904+18.12154i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_5 Sim_10 TrajSim_5_10
#> 2 -0.3993700+0.6920695i Traj_5 Sim_10 TrajSim_5_10
#> 3 -0.2087645+0.8487023i Traj_5 Sim_10 TrajSim_5_10
#> 4 -0.2877071+0.7210855i Traj_5 Sim_10 TrajSim_5_10
#> 5 -0.2655512+0.6317915i Traj_5 Sim_10 TrajSim_5_10
#> 6 -0.4100224+0.8120700i Traj_5 Sim_10 TrajSim_5_10
#> 7 -0.4195486+0.8378185i Traj_5 Sim_10 TrajSim_5_10
#>
#> [[10]][[6]]
#> x y time displacementTime polar
#> 1 26.19800 13.69800 0.00 0.00 26.19800+13.69800i
#> 2 25.69636 14.61200 0.02 0.02 25.69636+14.61200i
#> 3 25.14193 15.57835 0.04 0.04 25.14193+15.57835i
#> 4 24.56452 16.44844 0.06 0.06 24.56452+16.44844i
#> 5 23.98749 17.45725 0.08 0.08 23.98749+17.45725i
#> 6 23.33738 18.37515 0.10 0.10 23.33738+18.37515i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_6 Sim_10 TrajSim_6_10
#> 2 -0.5016426+0.9140030i Traj_6 Sim_10 TrajSim_6_10
#> 3 -0.5544260+0.9663478i Traj_6 Sim_10 TrajSim_6_10
#> 4 -0.5774141+0.8700926i Traj_6 Sim_10 TrajSim_6_10
#> 5 -0.5770261+1.0088032i Traj_6 Sim_10 TrajSim_6_10
#> 6 -0.6501073+0.9179049i Traj_6 Sim_10 TrajSim_6_10
#>
#> [[10]][[7]]
#> x y time displacementTime polar
#> 1 26.47200 15.49600 0.00 0.00 26.47200+15.49600i
#> 2 27.54471 15.03589 0.02 0.02 27.54471+15.03589i
#> 3 28.89484 14.45001 0.04 0.04 28.89484+14.45001i
#> 4 30.06915 13.98273 0.06 0.06 30.06915+13.98273i
#> 5 30.95753 13.46944 0.08 0.08 30.95753+13.46944i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_7 Sim_10 TrajSim_7_10
#> 2 1.0727138-0.4601052i Traj_7 Sim_10 TrajSim_7_10
#> 3 1.3501221-0.5858817i Traj_7 Sim_10 TrajSim_7_10
#> 4 1.1743175-0.4672862i Traj_7 Sim_10 TrajSim_7_10
#> 5 0.8883806-0.5132903i Traj_7 Sim_10 TrajSim_7_10
#>
#> [[10]][[8]]
#> x y time displacementTime polar
#> 1 13.21800 8.752000 0.00 0.00 13.21800+8.752000i
#> 2 12.90750 8.500768 0.02 0.02 12.90750+8.500768i
#> 3 12.49242 8.323159 0.04 0.04 12.49242+8.323159i
#> 4 12.07928 8.297601 0.06 0.06 12.07928+8.297601i
#> 5 11.70588 8.332358 0.08 0.08 11.70588+8.332358i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.00000000i Traj_8 Sim_10 TrajSim_8_10
#> 2 -0.3105044-0.25123226i Traj_8 Sim_10 TrajSim_8_10
#> 3 -0.4150791-0.17760879i Traj_8 Sim_10 TrajSim_8_10
#> 4 -0.4131321-0.02555783i Traj_8 Sim_10 TrajSim_8_10
#> 5 -0.3734083+0.03475692i Traj_8 Sim_10 TrajSim_8_10
#>
#> [[10]][[9]]
#> x y time displacementTime polar
#> 1 15.63800 8.164000 0.00 0.00 15.63800+ 8.164000i
#> 2 15.11956 9.101016 0.02 0.02 15.11956+ 9.101016i
#> 3 14.73234 10.028989 0.04 0.04 14.73234+10.028989i
#> 4 14.32683 11.028708 0.06 0.06 14.32683+11.028708i
#> 5 13.88788 12.059419 0.08 0.08 13.88788+12.059419i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_9 Sim_10 TrajSim_9_10
#> 2 -0.5184370+0.9370155i Traj_9 Sim_10 TrajSim_9_10
#> 3 -0.3872183+0.9279734i Traj_9 Sim_10 TrajSim_9_10
#> 4 -0.4055171+0.9997189i Traj_9 Sim_10 TrajSim_9_10
#> 5 -0.4389508+1.0307110i Traj_9 Sim_10 TrajSim_9_10
#>
#> [[10]][[10]]
#> x y time displacementTime polar
#> 1 14.69800 6.798000 0.00 0.00 14.69800+ 6.798000i
#> 2 14.18047 7.561005 0.02 0.02 14.18047+ 7.561005i
#> 3 13.68797 8.319933 0.04 0.04 13.68797+ 8.319933i
#> 4 13.21748 9.044428 0.06 0.06 13.21748+ 9.044428i
#> 5 12.71969 9.723468 0.08 0.08 12.71969+ 9.723468i
#> 6 12.22598 10.340588 0.10 0.10 12.22598+10.340588i
#> 7 11.73256 11.028097 0.12 0.12 11.73256+11.028097i
#> 8 11.26892 11.818682 0.14 0.14 11.26892+11.818682i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_10 Sim_10 TrajSim_10_10
#> 2 -0.5175272+0.7630054i Traj_10 Sim_10 TrajSim_10_10
#> 3 -0.4925049+0.7589276i Traj_10 Sim_10 TrajSim_10_10
#> 4 -0.4704848+0.7244953i Traj_10 Sim_10 TrajSim_10_10
#> 5 -0.4977936+0.6790402i Traj_10 Sim_10 TrajSim_10_10
#> 6 -0.4937055+0.6171194i Traj_10 Sim_10 TrajSim_10_10
#> 7 -0.4934216+0.6875091i Traj_10 Sim_10 TrajSim_10_10
#> 8 -0.4636383+0.7905847i Traj_10 Sim_10 TrajSim_10_10
#>
#> [[10]][[11]]
#> x y time displacementTime polar
#> 1 12.00600 7.316000 0.00 0.00 12.00600+ 7.316000i
#> 2 11.64173 8.273527 0.02 0.02 11.64173+ 8.273527i
#> 3 11.28950 9.260285 0.04 0.04 11.28950+ 9.260285i
#> 4 11.02572 10.141263 0.06 0.06 11.02572+10.141263i
#> 5 10.69353 11.228142 0.08 0.08 10.69353+11.228142i
#> displacement Trajectory Simulation TrajSim
#> 1 0.0000000+0.0000000i Traj_11 Sim_10 TrajSim_11_10
#> 2 -0.3642750+0.9575272i Traj_11 Sim_10 TrajSim_11_10
#> 3 -0.3522230+0.9867575i Traj_11 Sim_10 TrajSim_11_10
#> 4 -0.2637851+0.8809781i Traj_11 Sim_10 TrajSim_11_10
#> 5 -0.3321900+1.0868790i Traj_11 Sim_10 TrajSim_11_10Plotting Simulated and Actual Tracks
The plot_sim() function provides a
visual comparison between simulated movement
trajectories and the actual observed tracks,
allowing users to evaluate how closely the simulations replicate
real movement patterns. The function requires two main
inputs: a track R object representing the
original track data and a track simulation R
object generated by the
simulate_track() function, which contains
the simulated trajectories to be compared against the original
tracks.
The function relies on the ggplot2
package to create plots with two primary components: simulated
and actual trajectories. Simulated
trajectories are displayed with paths colored according to the
user-specified colors via the colours_sim
argument. The user can also adjust transparency and
line width through the
alpha_sim and
lwd_sim arguments. The default color for
simulated tracks is black, and the default transparency
level is set to a low value (0.1) to avoid
visual clutter when many simulated tracks are plotted. The
original trajectories are plotted on top of the
simulated trajectories using the colors specified by the
colours_act argument. Users can also
adjust transparency
(alpha_act) and line
width (lwd_act) to enhance
visibility. This overlay helps in visually comparing the
similarity between actual and simulated tracks.
The function returns a ggplot R object
that overlays the original and simulated tracks, allowing for further
customization using additional ggplot2
functions if desired. This visualization tool is essential for assessing
whether the chosen simulation model (Directed,
Constrained, or Unconstrained)
adequately captures the movement dynamics represented
by the original tracks and for comparing how well a specific model
replicates the original track patterns under various conditions.
Examples of Usage
Visualizing the Unconstrained simulation for the Paluxy River
dataset using default settings.
This plot provides a basic comparison of the simulated tracks over the
original tracks.
plot_sim(PaluxyRiver, sim_unconstrained_paluxy)
Visualizing the Directed simulation for the Paluxy River dataset with customized colors, transparency, and line width. Simulated tracks are plotted using light blue and orange colors with moderate transparency, making them easily distinguishable from the actual tracks plotted in black.
plot_sim(PaluxyRiver, sim_directed_paluxy,
colours_sim = c("#E69F00", "#56B4E9"),
alpha_sim = 0.4, lwd_sim = 1,
colours_act = c("black", "black"), alpha_act = 0.7, lwd_act = 2
)
Visualizing the Constrained simulation for the Paluxy River dataset with enhanced transparency and a reduced line width for the simulated tracks. This approach highlights the actual tracks more clearly, emphasizing the contrast between real and simulated data.
plot_sim(PaluxyRiver, sim_constrained_paluxy,
colours_sim = c("#E69F00", "#56B4E9"),
alpha_sim = 0.6, lwd_sim = 0.1,
alpha_act = 0.5, lwd_act = 2
)
Visualizing the Unconstrained simulation for the MountTom
dataset using default settings.
This plot provides a straightforward comparison of the simulated tracks
over the actual tracks without any customization.
plot_sim(sbMountTom, sim_unconstrained_mount)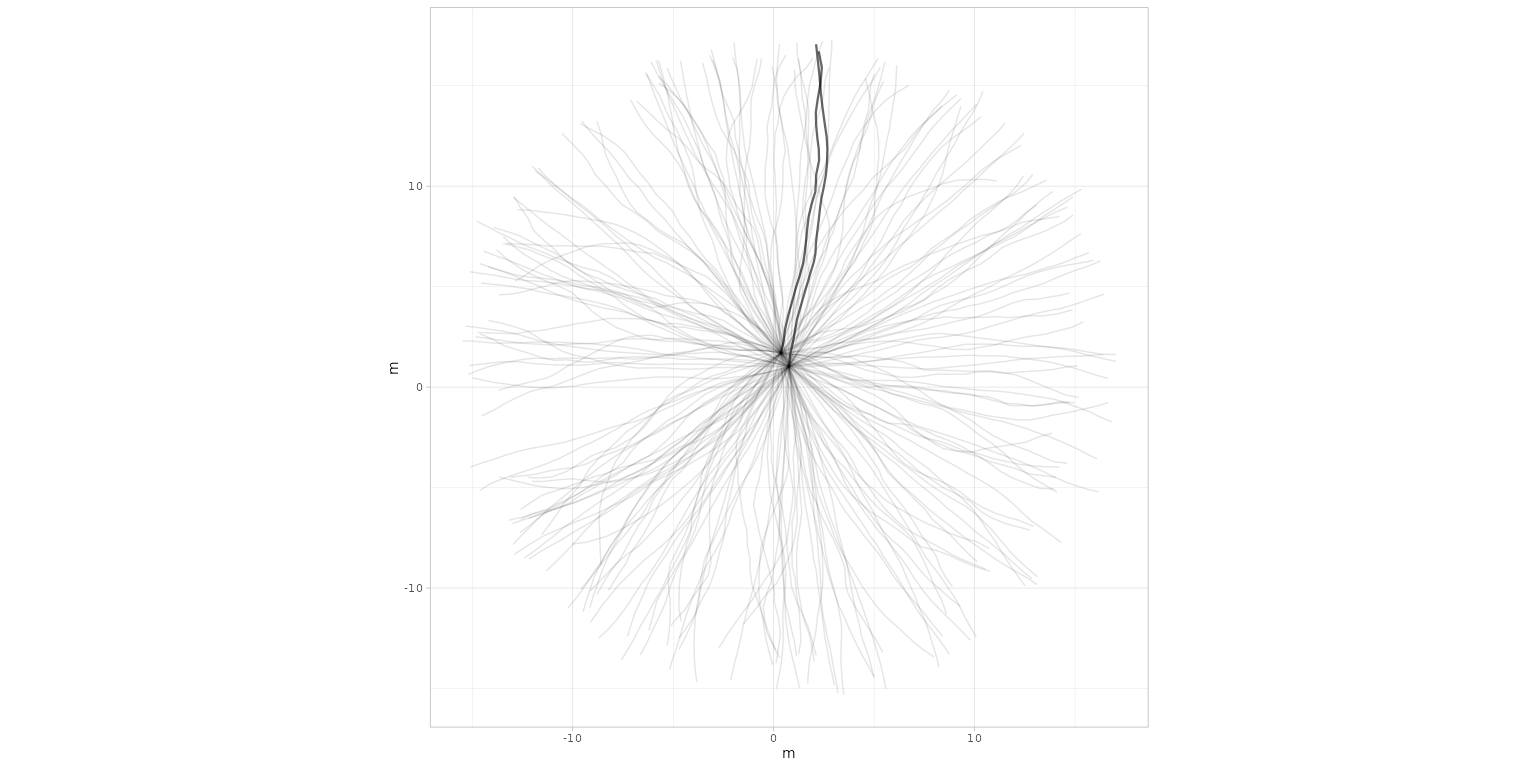
Visualizing the Directed simulation for the MountTom dataset with a custom color palette, higher transparency, and thicker lines for simulated tracks. This setup allows for better differentiation between the various simulated tracks and the original ones.
plot_sim(sbMountTom, sim_directed_mount,
colours_sim = c("#6BAED6", "#FF7F00", "#1F77B4", "#D62728",
"#2CA02C", "#9467BD", "#8C564B", "#E377C2",
"#7F7F7F", "#BCBD22", "#17BECF"),
alpha_sim = 0.3, lwd_sim = 1.5,
alpha_act = 0.8, lwd_act = 2
)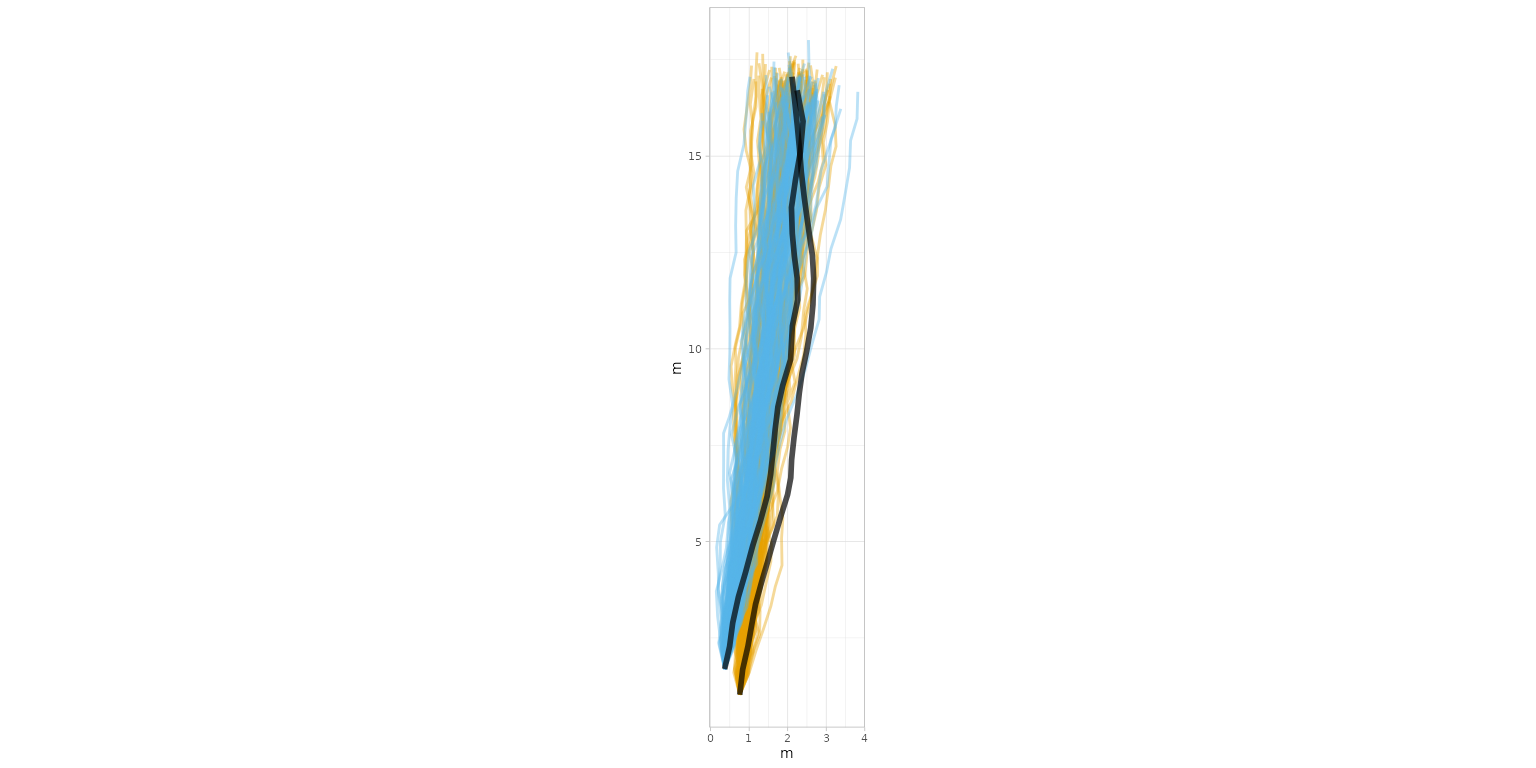
Visualizing the Constrained simulation for the MountTom dataset with a diverse color palette and thinner simulated tracks for better clarity. The high transparency of simulated tracks ensures the original tracks remain clearly visible.
plot_sim(sbMountTom, sim_constrained_mount,
colours_sim = c("#6BAED6", "#FF7F00", "#1F77B4", "#D62728",
"#2CA02C", "#9467BD", "#8C564B", "#E377C2",
"#7F7F7F", "#BCBD22", "#17BECF"),
alpha_sim = 0.5, lwd_sim = 0.2,
alpha_act = 0.6, lwd_act = 2
)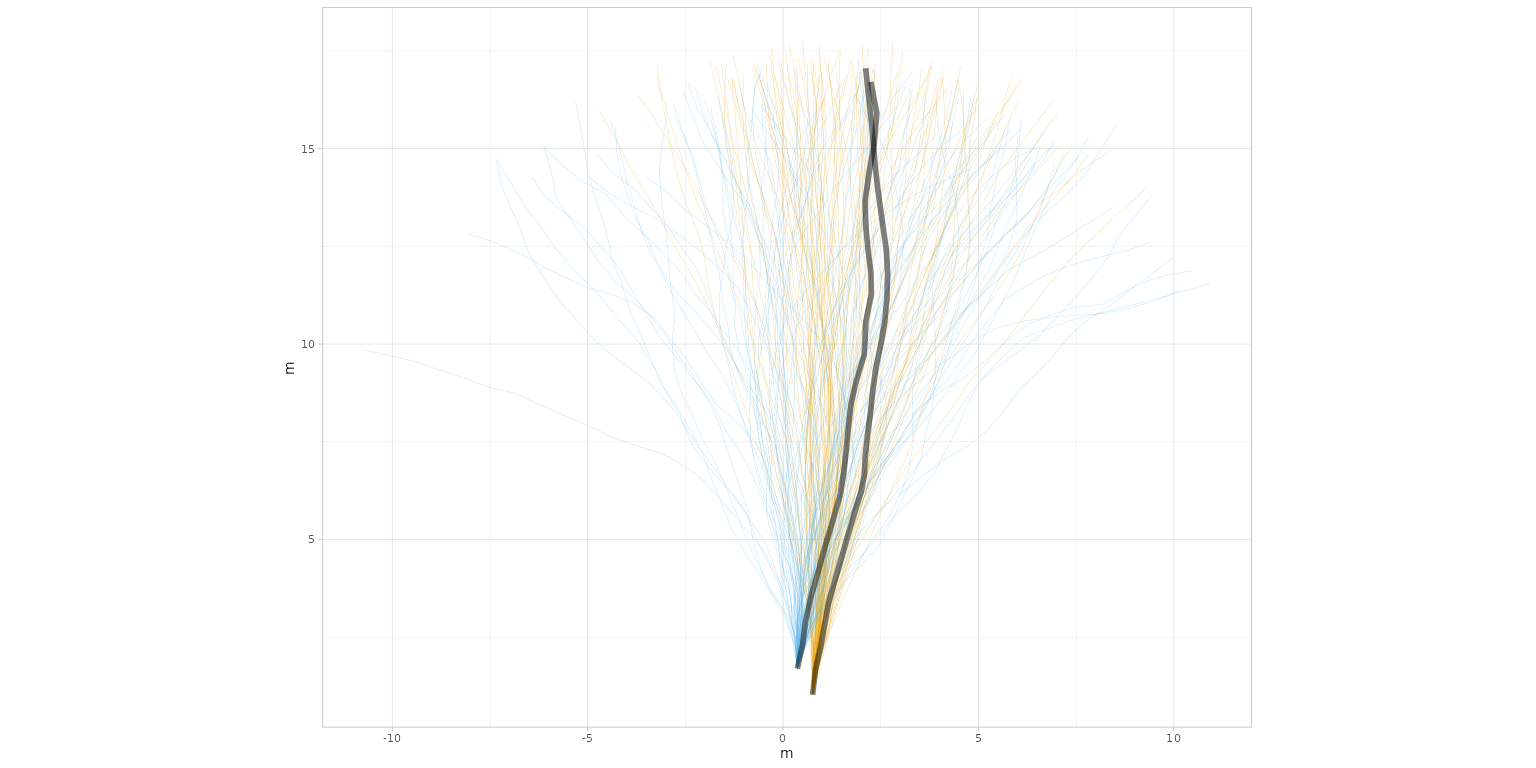
Similarity Metric Calculation using Dynamic Time Warping (DTW) and Fréchet Distance
The simil_DTW_metric() and
simil_Frechet_metric() functions provide
robust tools for comparing movement trajectories by
quantifying their similarity through distinct mathematical approaches.
Both functions operate on a track R
object, allowing users to evaluate whether observed patterns
deviate from random expectations by comparing real tracks to simulated
ones.
The simil_DTW_metric() function applies
the Dynamic Time Warping (DTW) algorithm, which is
especially suitable for analyzing animal movement
patterns with temporal distortions or varying
lengths. By minimizing the cumulative distance between
corresponding points, it effectively aligns sequences even when
timing or pacing differs between trajectories. The calculation uses the
dtw::dtw() function from the
dtw package, employing Euclidean
distance to compute local distances between points. This method
excels at assessing how well simulated tracks replicate real movements,
although it can be sensitive to noise and outliers, particularly when
comparing trajectories of different lengths.
In contrast, the simil_Frechet_metric()
function calculates similarity based on the Fréchet
distance, a metric that evaluates the overall shape of
trajectories by considering both the order and location
of points. Unlike DTW, which focuses on pointwise alignment,
the Fréchet distance measures similarity by assessing how closely two
paths follow each other over their entire length. This approach is often
illustrated by the analogy of a person walking a dog on a
leash, where both can adjust their speed independently but must
remain connected. It is particularly effective for comparing
trajectories where the overall path shape matters, such as
migration routes, travel paths, or animal tracks.
However, because the Fréchet distance evaluates all points along the
path, this method is particularly sensitive to noise
and may return an invalid measurement (-1) when
comparing highly disparate tracks, especially those generated under
fully Unconstrained models. It is essential for users
to check for the presence of -1 values in the resulting
track similarity R object, as these
invalid measurements cannot be used in further analyses. Ignoring this
warning may lead to incorrect conclusions or errors when processing the
results.
Both functions include the
superposition argument, which provides
options for aligning trajectories before calculating similarity metrics:
"None",
"Centroid", and
"Origin". The
"None" option compares trajectories as
they are, while "Centroid" alignment
shifts trajectories to their centroids, eliminating positional
differences while preserving shape. The
"Origin" option aligns trajectories to
their starting points, making comparisons independent of absolute
positions. These alignment methods ensure comparisons are based on
movement patterns rather than arbitrary spatial
differences.
Statistical testing is supported when
test = TRUE, requiring a
track simulation R object to be provided
through the sim argument. This allows
users to compare similarity metrics between real tracks and simulated
trajectories, determining whether observed similarities are
significantly greater than those expected under random conditions. The
functions provide two types of p-values:
pairwise p-values, which represent the
proportion of simulated distances smaller than the observed distance for
each trajectory pair, and combined p-values,
which reflect the overall proportion of simulations where all observed
distances are smaller than the simulated ones. This statistical
framework offers a comprehensive approach for evaluating similarity
metrics and testing hypotheses about track similarity.
The simil_DTW_metric() and
simil_Frechet_metric() functions return a
track similarity R object, which contains
valuable information about the similarity between trajectories. This
object includes a matrix called
DTW_distance_metric (for the DTW metric)
or Frechet_distance_metric (for the
Fréchet metric), which stores the pairwise distances calculated between
all trajectories. If the test argument is
set to TRUE, additional components are
included in the output. Specifically, a matrix of
DTW_distance_metric_p_values or
Frechet_distance_metric_p_values is
provided, containing the p-values for the pairwise distances
obtained by comparing the observed tracks to those generated through
simulations. The
DTW_metric_p_values_combined and
Frechet_metric_p_values_combined elements
report the overall p-value, summarizing the significance of the
similarity between all tracks when considering the simulated datasets.
Moreover, the output includes
DTW_distance_metric_simulations or
Frechet_distance_metric_simulations, a
list of matrices with the similarity metrics calculated from each
simulated dataset. This comprehensive output structure allows users to
thoroughly evaluate whether the observed similarity between trajectories
is greater than expected under random conditions, providing robust
statistical support for their analyses.
The combination of flexible alignment options, statistical testing, and compatibility with simulated datasets makes these functions highly valuable for investigating animal movement patterns, testing hypotheses about track similarity, and assessing the accuracy of simulations.
Examples of Usage
Comparing Paluxy River tracks against Directed model simulations using Centroid superposition.
simil_dtw_directed_paluxy <- simil_DTW_metric(PaluxyRiver, test = TRUE,
sim = sim_directed_paluxy,
superposition = "Centroid")#> $DTW_distance_metric
#> Trackway_1 Trackway_2
#> Trackway_1 NA 7.060018
#> Trackway_2 7.060018 NA
#>
#> $DTW_distance_metric_p_values
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.1584158
#> Trackway_2 0.1584158 NA
#>
#> $DTW_distance_metric_p_values_BH
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.1584158
#> Trackway_2 0.1584158 NA
#>
#> $DTW_metric_p_values_combined
#> [1] 0.15
#>
#> $DTW_distance_metric_simulations
#> $DTW_distance_metric_simulations[[1]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 12.70263
#> Trackway_2 12.70263 NA
#>
#> $DTW_distance_metric_simulations[[2]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 9.233379
#> Trackway_2 9.233379 NA
#>
#> $DTW_distance_metric_simulations[[3]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 11.10348
#> Trackway_2 11.10348 NA
#>
#> $DTW_distance_metric_simulations[[4]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 10.49878
#> Trackway_2 10.49878 NA
#>
#> $DTW_distance_metric_simulations[[5]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 7.471062
#> Trackway_2 7.471062 NA
#>
#> $DTW_distance_metric_simulations[[6]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 8.472645
#> Trackway_2 8.472645 NA
#>
#> $DTW_distance_metric_simulations[[7]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 8.081452
#> Trackway_2 8.081452 NA
#>
#> $DTW_distance_metric_simulations[[8]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 11.47983
#> Trackway_2 11.47983 NA
#>
#> $DTW_distance_metric_simulations[[9]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 6.832365
#> Trackway_2 6.832365 NA
#>
#> $DTW_distance_metric_simulations[[10]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 7.926633
#> Trackway_2 7.926633 NA
#>
#> $DTW_distance_metric_simulations[[11]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 7.266971
#> Trackway_2 7.266971 NA
#>
#> $DTW_distance_metric_simulations[[12]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 7.450125
#> Trackway_2 7.450125 NA
#>
#> $DTW_distance_metric_simulations[[13]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 14.84276
#> Trackway_2 14.84276 NA
#>
#> $DTW_distance_metric_simulations[[14]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 5.203299
#> Trackway_2 5.203299 NA
#>
#> $DTW_distance_metric_simulations[[15]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 12.24169
#> Trackway_2 12.24169 NA
#>
#> $DTW_distance_metric_simulations[[16]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 8.803208
#> Trackway_2 8.803208 NA
#>
#> $DTW_distance_metric_simulations[[17]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 14.40755
#> Trackway_2 14.40755 NA
#>
#> $DTW_distance_metric_simulations[[18]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 8.838549
#> Trackway_2 8.838549 NA
#>
#> $DTW_distance_metric_simulations[[19]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 7.247482
#> Trackway_2 7.247482 NA
#>
#> $DTW_distance_metric_simulations[[20]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 8.408338
#> Trackway_2 8.408338 NA
#>
#> $DTW_distance_metric_simulations[[21]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 8.033847
#> Trackway_2 8.033847 NA
#>
#> $DTW_distance_metric_simulations[[22]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 11.97456
#> Trackway_2 11.97456 NA
#>
#> $DTW_distance_metric_simulations[[23]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 6.924495
#> Trackway_2 6.924495 NA
#>
#> $DTW_distance_metric_simulations[[24]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 7.783489
#> Trackway_2 7.783489 NA
#>
#> $DTW_distance_metric_simulations[[25]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 6.741306
#> Trackway_2 6.741306 NA
#>
#> $DTW_distance_metric_simulations[[26]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 7.683001
#> Trackway_2 7.683001 NA
#>
#> $DTW_distance_metric_simulations[[27]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 7.121962
#> Trackway_2 7.121962 NA
#>
#> $DTW_distance_metric_simulations[[28]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 9.132016
#> Trackway_2 9.132016 NA
#>
#> $DTW_distance_metric_simulations[[29]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 9.195486
#> Trackway_2 9.195486 NA
#>
#> $DTW_distance_metric_simulations[[30]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 5.775831
#> Trackway_2 5.775831 NA
#>
#> $DTW_distance_metric_simulations[[31]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 6.696432
#> Trackway_2 6.696432 NA
#>
#> $DTW_distance_metric_simulations[[32]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 8.461733
#> Trackway_2 8.461733 NA
#>
#> $DTW_distance_metric_simulations[[33]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 13.7823
#> Trackway_2 13.7823 NA
#>
#> $DTW_distance_metric_simulations[[34]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 6.295806
#> Trackway_2 6.295806 NA
#>
#> $DTW_distance_metric_simulations[[35]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 7.721686
#> Trackway_2 7.721686 NA
#>
#> $DTW_distance_metric_simulations[[36]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 8.618914
#> Trackway_2 8.618914 NA
#>
#> $DTW_distance_metric_simulations[[37]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 12.42471
#> Trackway_2 12.42471 NA
#>
#> $DTW_distance_metric_simulations[[38]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 10.05827
#> Trackway_2 10.05827 NA
#>
#> $DTW_distance_metric_simulations[[39]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 13.08326
#> Trackway_2 13.08326 NA
#>
#> $DTW_distance_metric_simulations[[40]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 11.5959
#> Trackway_2 11.5959 NA
#>
#> $DTW_distance_metric_simulations[[41]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 7.888192
#> Trackway_2 7.888192 NA
#>
#> $DTW_distance_metric_simulations[[42]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 10.11984
#> Trackway_2 10.11984 NA
#>
#> $DTW_distance_metric_simulations[[43]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 7.996868
#> Trackway_2 7.996868 NA
#>
#> $DTW_distance_metric_simulations[[44]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 6.534561
#> Trackway_2 6.534561 NA
#>
#> $DTW_distance_metric_simulations[[45]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 6.845402
#> Trackway_2 6.845402 NA
#>
#> $DTW_distance_metric_simulations[[46]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 11.6924
#> Trackway_2 11.6924 NA
#>
#> $DTW_distance_metric_simulations[[47]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 9.500664
#> Trackway_2 9.500664 NA
#>
#> $DTW_distance_metric_simulations[[48]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 6.944077
#> Trackway_2 6.944077 NA
#>
#> $DTW_distance_metric_simulations[[49]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 8.879863
#> Trackway_2 8.879863 NA
#>
#> $DTW_distance_metric_simulations[[50]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 9.316639
#> Trackway_2 9.316639 NA
#>
#> $DTW_distance_metric_simulations[[51]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 8.492826
#> Trackway_2 8.492826 NA
#>
#> $DTW_distance_metric_simulations[[52]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 10.84308
#> Trackway_2 10.84308 NA
#>
#> $DTW_distance_metric_simulations[[53]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 8.402731
#> Trackway_2 8.402731 NA
#>
#> $DTW_distance_metric_simulations[[54]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 7.323275
#> Trackway_2 7.323275 NA
#>
#> $DTW_distance_metric_simulations[[55]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 15.44575
#> Trackway_2 15.44575 NA
#>
#> $DTW_distance_metric_simulations[[56]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 7.192298
#> Trackway_2 7.192298 NA
#>
#> $DTW_distance_metric_simulations[[57]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 11.13226
#> Trackway_2 11.13226 NA
#>
#> $DTW_distance_metric_simulations[[58]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 14.65892
#> Trackway_2 14.65892 NA
#>
#> $DTW_distance_metric_simulations[[59]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 10.17895
#> Trackway_2 10.17895 NA
#>
#> $DTW_distance_metric_simulations[[60]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 14.44872
#> Trackway_2 14.44872 NA
#>
#> $DTW_distance_metric_simulations[[61]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 9.23964
#> Trackway_2 9.23964 NA
#>
#> $DTW_distance_metric_simulations[[62]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 8.534246
#> Trackway_2 8.534246 NA
#>
#> $DTW_distance_metric_simulations[[63]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 24.02733
#> Trackway_2 24.02733 NA
#>
#> $DTW_distance_metric_simulations[[64]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 8.218288
#> Trackway_2 8.218288 NA
#>
#> $DTW_distance_metric_simulations[[65]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 7.797672
#> Trackway_2 7.797672 NA
#>
#> $DTW_distance_metric_simulations[[66]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 11.69146
#> Trackway_2 11.69146 NA
#>
#> $DTW_distance_metric_simulations[[67]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 13.86343
#> Trackway_2 13.86343 NA
#>
#> $DTW_distance_metric_simulations[[68]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 9.900959
#> Trackway_2 9.900959 NA
#>
#> $DTW_distance_metric_simulations[[69]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 8.385225
#> Trackway_2 8.385225 NA
#>
#> $DTW_distance_metric_simulations[[70]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 8.263558
#> Trackway_2 8.263558 NA
#>
#> $DTW_distance_metric_simulations[[71]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 8.484855
#> Trackway_2 8.484855 NA
#>
#> $DTW_distance_metric_simulations[[72]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 10.39251
#> Trackway_2 10.39251 NA
#>
#> $DTW_distance_metric_simulations[[73]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 9.251219
#> Trackway_2 9.251219 NA
#>
#> $DTW_distance_metric_simulations[[74]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 7.299127
#> Trackway_2 7.299127 NA
#>
#> $DTW_distance_metric_simulations[[75]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 7.946392
#> Trackway_2 7.946392 NA
#>
#> $DTW_distance_metric_simulations[[76]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 6.977214
#> Trackway_2 6.977214 NA
#>
#> $DTW_distance_metric_simulations[[77]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 10.59017
#> Trackway_2 10.59017 NA
#>
#> $DTW_distance_metric_simulations[[78]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 8.378536
#> Trackway_2 8.378536 NA
#>
#> $DTW_distance_metric_simulations[[79]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 8.772803
#> Trackway_2 8.772803 NA
#>
#> $DTW_distance_metric_simulations[[80]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 13.63827
#> Trackway_2 13.63827 NA
#>
#> $DTW_distance_metric_simulations[[81]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 7.638815
#> Trackway_2 7.638815 NA
#>
#> $DTW_distance_metric_simulations[[82]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 6.298097
#> Trackway_2 6.298097 NA
#>
#> $DTW_distance_metric_simulations[[83]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 7.113214
#> Trackway_2 7.113214 NA
#>
#> $DTW_distance_metric_simulations[[84]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 10.24538
#> Trackway_2 10.24538 NA
#>
#> $DTW_distance_metric_simulations[[85]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 7.694775
#> Trackway_2 7.694775 NA
#>
#> $DTW_distance_metric_simulations[[86]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 10.57176
#> Trackway_2 10.57176 NA
#>
#> $DTW_distance_metric_simulations[[87]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 8.89937
#> Trackway_2 8.89937 NA
#>
#> $DTW_distance_metric_simulations[[88]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 14.298
#> Trackway_2 14.298 NA
#>
#> $DTW_distance_metric_simulations[[89]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 5.69897
#> Trackway_2 5.69897 NA
#>
#> $DTW_distance_metric_simulations[[90]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 11.08674
#> Trackway_2 11.08674 NA
#>
#> $DTW_distance_metric_simulations[[91]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 7.641014
#> Trackway_2 7.641014 NA
#>
#> $DTW_distance_metric_simulations[[92]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 7.229382
#> Trackway_2 7.229382 NA
#>
#> $DTW_distance_metric_simulations[[93]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 11.13141
#> Trackway_2 11.13141 NA
#>
#> $DTW_distance_metric_simulations[[94]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 6.116763
#> Trackway_2 6.116763 NA
#>
#> $DTW_distance_metric_simulations[[95]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 6.292158
#> Trackway_2 6.292158 NA
#>
#> $DTW_distance_metric_simulations[[96]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 10.31642
#> Trackway_2 10.31642 NA
#>
#> $DTW_distance_metric_simulations[[97]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 8.250661
#> Trackway_2 8.250661 NA
#>
#> $DTW_distance_metric_simulations[[98]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 7.163862
#> Trackway_2 7.163862 NA
#>
#> $DTW_distance_metric_simulations[[99]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 14.30575
#> Trackway_2 14.30575 NA
#>
#> $DTW_distance_metric_simulations[[100]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 10.04254
#> Trackway_2 10.04254 NA
simil_frechet_directed_paluxy <- simil_Frechet_metric(PaluxyRiver, test = TRUE,
sim = sim_directed_paluxy,
superposition = "Centroid")#> $Frechet_distance_metric
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.6067683
#> Trackway_2 0.6067683 NA
#>
#> $Frechet_distance_metric_p_values
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.2772277
#> Trackway_2 0.2772277 NA
#>
#> $Frechet_distance_metric_p_values_BH
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.2772277
#> Trackway_2 0.2772277 NA
#>
#> $Frechet_metric_p_values_combined
#> [1] 0.27
#>
#> $Frechet_distance_metric_simulations
#> $Frechet_distance_metric_simulations[[1]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.9594242
#> Trackway_2 0.9594242 NA
#>
#> $Frechet_distance_metric_simulations[[2]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.8532692
#> Trackway_2 0.8532692 NA
#>
#> $Frechet_distance_metric_simulations[[3]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.9142107
#> Trackway_2 0.9142107 NA
#>
#> $Frechet_distance_metric_simulations[[4]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.9651208
#> Trackway_2 0.9651208 NA
#>
#> $Frechet_distance_metric_simulations[[5]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.3807016
#> Trackway_2 0.3807016 NA
#>
#> $Frechet_distance_metric_simulations[[6]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.8954306
#> Trackway_2 0.8954306 NA
#>
#> $Frechet_distance_metric_simulations[[7]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.8166024
#> Trackway_2 0.8166024 NA
#>
#> $Frechet_distance_metric_simulations[[8]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.982561
#> Trackway_2 0.982561 NA
#>
#> $Frechet_distance_metric_simulations[[9]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.453864
#> Trackway_2 0.453864 NA
#>
#> $Frechet_distance_metric_simulations[[10]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.4873859
#> Trackway_2 0.4873859 NA
#>
#> $Frechet_distance_metric_simulations[[11]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.731644
#> Trackway_2 0.731644 NA
#>
#> $Frechet_distance_metric_simulations[[12]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.74581
#> Trackway_2 0.74581 NA
#>
#> $Frechet_distance_metric_simulations[[13]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.9933482
#> Trackway_2 0.9933482 NA
#>
#> $Frechet_distance_metric_simulations[[14]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.6250835
#> Trackway_2 0.6250835 NA
#>
#> $Frechet_distance_metric_simulations[[15]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.6652312
#> Trackway_2 0.6652312 NA
#>
#> $Frechet_distance_metric_simulations[[16]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.7340924
#> Trackway_2 0.7340924 NA
#>
#> $Frechet_distance_metric_simulations[[17]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 1.149257
#> Trackway_2 1.149257 NA
#>
#> $Frechet_distance_metric_simulations[[18]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.8707353
#> Trackway_2 0.8707353 NA
#>
#> $Frechet_distance_metric_simulations[[19]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.9413291
#> Trackway_2 0.9413291 NA
#>
#> $Frechet_distance_metric_simulations[[20]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 1.060765
#> Trackway_2 1.060765 NA
#>
#> $Frechet_distance_metric_simulations[[21]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.7237103
#> Trackway_2 0.7237103 NA
#>
#> $Frechet_distance_metric_simulations[[22]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 1.008842
#> Trackway_2 1.008842 NA
#>
#> $Frechet_distance_metric_simulations[[23]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.7712149
#> Trackway_2 0.7712149 NA
#>
#> $Frechet_distance_metric_simulations[[24]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.8563253
#> Trackway_2 0.8563253 NA
#>
#> $Frechet_distance_metric_simulations[[25]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.61941
#> Trackway_2 0.61941 NA
#>
#> $Frechet_distance_metric_simulations[[26]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.9917619
#> Trackway_2 0.9917619 NA
#>
#> $Frechet_distance_metric_simulations[[27]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.4124516
#> Trackway_2 0.4124516 NA
#>
#> $Frechet_distance_metric_simulations[[28]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.8310718
#> Trackway_2 0.8310718 NA
#>
#> $Frechet_distance_metric_simulations[[29]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.5684632
#> Trackway_2 0.5684632 NA
#>
#> $Frechet_distance_metric_simulations[[30]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.4810913
#> Trackway_2 0.4810913 NA
#>
#> $Frechet_distance_metric_simulations[[31]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.5954206
#> Trackway_2 0.5954206 NA
#>
#> $Frechet_distance_metric_simulations[[32]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.7165004
#> Trackway_2 0.7165004 NA
#>
#> $Frechet_distance_metric_simulations[[33]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.969535
#> Trackway_2 0.969535 NA
#>
#> $Frechet_distance_metric_simulations[[34]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.4480011
#> Trackway_2 0.4480011 NA
#>
#> $Frechet_distance_metric_simulations[[35]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.6066617
#> Trackway_2 0.6066617 NA
#>
#> $Frechet_distance_metric_simulations[[36]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.8321303
#> Trackway_2 0.8321303 NA
#>
#> $Frechet_distance_metric_simulations[[37]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.9325197
#> Trackway_2 0.9325197 NA
#>
#> $Frechet_distance_metric_simulations[[38]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.759643
#> Trackway_2 0.759643 NA
#>
#> $Frechet_distance_metric_simulations[[39]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.7658709
#> Trackway_2 0.7658709 NA
#>
#> $Frechet_distance_metric_simulations[[40]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.909121
#> Trackway_2 0.909121 NA
#>
#> $Frechet_distance_metric_simulations[[41]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.601396
#> Trackway_2 0.601396 NA
#>
#> $Frechet_distance_metric_simulations[[42]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 1.086054
#> Trackway_2 1.086054 NA
#>
#> $Frechet_distance_metric_simulations[[43]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.7169235
#> Trackway_2 0.7169235 NA
#>
#> $Frechet_distance_metric_simulations[[44]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.461591
#> Trackway_2 0.461591 NA
#>
#> $Frechet_distance_metric_simulations[[45]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.6626232
#> Trackway_2 0.6626232 NA
#>
#> $Frechet_distance_metric_simulations[[46]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 1.057266
#> Trackway_2 1.057266 NA
#>
#> $Frechet_distance_metric_simulations[[47]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.6818472
#> Trackway_2 0.6818472 NA
#>
#> $Frechet_distance_metric_simulations[[48]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.4829024
#> Trackway_2 0.4829024 NA
#>
#> $Frechet_distance_metric_simulations[[49]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.8029955
#> Trackway_2 0.8029955 NA
#>
#> $Frechet_distance_metric_simulations[[50]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.7211881
#> Trackway_2 0.7211881 NA
#>
#> $Frechet_distance_metric_simulations[[51]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.6686309
#> Trackway_2 0.6686309 NA
#>
#> $Frechet_distance_metric_simulations[[52]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.711767
#> Trackway_2 0.711767 NA
#>
#> $Frechet_distance_metric_simulations[[53]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.4329328
#> Trackway_2 0.4329328 NA
#>
#> $Frechet_distance_metric_simulations[[54]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.4272865
#> Trackway_2 0.4272865 NA
#>
#> $Frechet_distance_metric_simulations[[55]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 1.145588
#> Trackway_2 1.145588 NA
#>
#> $Frechet_distance_metric_simulations[[56]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.4836612
#> Trackway_2 0.4836612 NA
#>
#> $Frechet_distance_metric_simulations[[57]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 1.168087
#> Trackway_2 1.168087 NA
#>
#> $Frechet_distance_metric_simulations[[58]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.9088763
#> Trackway_2 0.9088763 NA
#>
#> $Frechet_distance_metric_simulations[[59]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.889594
#> Trackway_2 0.889594 NA
#>
#> $Frechet_distance_metric_simulations[[60]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 1.02766
#> Trackway_2 1.02766 NA
#>
#> $Frechet_distance_metric_simulations[[61]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.5990698
#> Trackway_2 0.5990698 NA
#>
#> $Frechet_distance_metric_simulations[[62]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 1.007118
#> Trackway_2 1.007118 NA
#>
#> $Frechet_distance_metric_simulations[[63]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 1.750963
#> Trackway_2 1.750963 NA
#>
#> $Frechet_distance_metric_simulations[[64]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.7158945
#> Trackway_2 0.7158945 NA
#>
#> $Frechet_distance_metric_simulations[[65]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.996137
#> Trackway_2 0.996137 NA
#>
#> $Frechet_distance_metric_simulations[[66]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.6764692
#> Trackway_2 0.6764692 NA
#>
#> $Frechet_distance_metric_simulations[[67]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 1.228326
#> Trackway_2 1.228326 NA
#>
#> $Frechet_distance_metric_simulations[[68]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.7487315
#> Trackway_2 0.7487315 NA
#>
#> $Frechet_distance_metric_simulations[[69]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.5333364
#> Trackway_2 0.5333364 NA
#>
#> $Frechet_distance_metric_simulations[[70]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.6524142
#> Trackway_2 0.6524142 NA
#>
#> $Frechet_distance_metric_simulations[[71]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.6897595
#> Trackway_2 0.6897595 NA
#>
#> $Frechet_distance_metric_simulations[[72]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 1.018857
#> Trackway_2 1.018857 NA
#>
#> $Frechet_distance_metric_simulations[[73]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.789176
#> Trackway_2 0.789176 NA
#>
#> $Frechet_distance_metric_simulations[[74]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.6078843
#> Trackway_2 0.6078843 NA
#>
#> $Frechet_distance_metric_simulations[[75]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.5800645
#> Trackway_2 0.5800645 NA
#>
#> $Frechet_distance_metric_simulations[[76]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.3252825
#> Trackway_2 0.3252825 NA
#>
#> $Frechet_distance_metric_simulations[[77]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 1.280775
#> Trackway_2 1.280775 NA
#>
#> $Frechet_distance_metric_simulations[[78]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.918491
#> Trackway_2 0.918491 NA
#>
#> $Frechet_distance_metric_simulations[[79]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.7598167
#> Trackway_2 0.7598167 NA
#>
#> $Frechet_distance_metric_simulations[[80]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 1.160987
#> Trackway_2 1.160987 NA
#>
#> $Frechet_distance_metric_simulations[[81]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.9467812
#> Trackway_2 0.9467812 NA
#>
#> $Frechet_distance_metric_simulations[[82]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.5682953
#> Trackway_2 0.5682953 NA
#>
#> $Frechet_distance_metric_simulations[[83]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.7770467
#> Trackway_2 0.7770467 NA
#>
#> $Frechet_distance_metric_simulations[[84]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.9267091
#> Trackway_2 0.9267091 NA
#>
#> $Frechet_distance_metric_simulations[[85]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.7436739
#> Trackway_2 0.7436739 NA
#>
#> $Frechet_distance_metric_simulations[[86]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.774653
#> Trackway_2 0.774653 NA
#>
#> $Frechet_distance_metric_simulations[[87]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.4729342
#> Trackway_2 0.4729342 NA
#>
#> $Frechet_distance_metric_simulations[[88]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 1.085641
#> Trackway_2 1.085641 NA
#>
#> $Frechet_distance_metric_simulations[[89]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.4017891
#> Trackway_2 0.4017891 NA
#>
#> $Frechet_distance_metric_simulations[[90]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.5996832
#> Trackway_2 0.5996832 NA
#>
#> $Frechet_distance_metric_simulations[[91]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.6873784
#> Trackway_2 0.6873784 NA
#>
#> $Frechet_distance_metric_simulations[[92]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.4181764
#> Trackway_2 0.4181764 NA
#>
#> $Frechet_distance_metric_simulations[[93]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.9504715
#> Trackway_2 0.9504715 NA
#>
#> $Frechet_distance_metric_simulations[[94]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.2896453
#> Trackway_2 0.2896453 NA
#>
#> $Frechet_distance_metric_simulations[[95]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.3756861
#> Trackway_2 0.3756861 NA
#>
#> $Frechet_distance_metric_simulations[[96]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.7996827
#> Trackway_2 0.7996827 NA
#>
#> $Frechet_distance_metric_simulations[[97]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.6093757
#> Trackway_2 0.6093757 NA
#>
#> $Frechet_distance_metric_simulations[[98]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.4623654
#> Trackway_2 0.4623654 NA
#>
#> $Frechet_distance_metric_simulations[[99]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.8680033
#> Trackway_2 0.8680033 NA
#>
#> $Frechet_distance_metric_simulations[[100]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.6634359
#> Trackway_2 0.6634359 NAComparing MountTom tracks (after subsetting) against Constrained model simulations using Origin superposition.
simil_dtw_constrained_mount <- simil_DTW_metric(sbMountTom, test = TRUE,
sim = sim_constrained_mount,
superposition = "Origin")#> $DTW_distance_metric
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 3.876534 6.429059 9.885858 11.307932
#> Trackway_02 3.876534 NA 7.846891 10.534176 10.426349
#> Trackway_03 6.429059 7.846891 NA 1.939701 4.956831
#> Trackway_04 9.885858 10.534176 1.939701 NA 3.092768
#> Trackway_07 11.307932 10.426349 4.956831 3.092768 NA
#> Trackway_08 8.723210 7.628799 3.380235 2.122137 2.598978
#> Trackway_09 44.872996 45.542538 23.858272 22.402666 27.585159
#> Trackway_13 33.004458 34.588263 12.530114 11.987635 18.011211
#> Trackway_15 13.301452 12.848699 3.628313 1.888562 1.928924
#> Trackway_16 7.506771 5.093868 6.520839 6.256540 4.535128
#> Trackway_18 15.251042 14.217558 4.517740 2.899849 2.940807
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 8.723210 44.87300 33.00446 13.301452 7.506771
#> Trackway_02 7.628799 45.54254 34.58826 12.848699 5.093868
#> Trackway_03 3.380235 23.85827 12.53011 3.628313 6.520839
#> Trackway_04 2.122137 22.40267 11.98763 1.888562 6.256540
#> Trackway_07 2.598978 27.58516 18.01121 1.928924 4.535128
#> Trackway_08 NA 27.90917 17.88413 2.906114 3.233682
#> Trackway_09 27.909168 NA 14.81310 21.574939 36.831213
#> Trackway_13 17.884132 14.81310 NA 12.398830 26.638818
#> Trackway_15 2.906114 21.57494 12.39883 NA 6.149675
#> Trackway_16 3.233682 36.83121 26.63882 6.149675 NA
#> Trackway_18 3.834832 21.93954 13.44764 1.262213 7.245713
#> Trackway_18
#> Trackway_01 15.251042
#> Trackway_02 14.217558
#> Trackway_03 4.517740
#> Trackway_04 2.899849
#> Trackway_07 2.940807
#> Trackway_08 3.834832
#> Trackway_09 21.939540
#> Trackway_13 13.447642
#> Trackway_15 1.262213
#> Trackway_16 7.245713
#> Trackway_18 NA
#>
#> $DTW_distance_metric_p_values
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0.20792079 0.00990099 0.81188119 0.88118812
#> Trackway_02 0.20792079 NA 0.48514851 0.92079208 0.99009901
#> Trackway_03 0.00990099 0.48514851 NA 0.00990099 0.70297030
#> Trackway_04 0.81188119 0.92079208 0.00990099 NA 0.00990099
#> Trackway_07 0.88118812 0.99009901 0.70297030 0.00990099 NA
#> Trackway_08 0.28712871 0.80198020 0.56435644 0.00990099 0.69306931
#> Trackway_09 1.00000000 1.00000000 1.00000000 1.00000000 1.00000000
#> Trackway_13 1.00000000 1.00000000 1.00000000 0.86138614 1.00000000
#> Trackway_15 0.00990099 0.00990099 0.00990099 0.00990099 0.00990099
#> Trackway_16 0.00990099 0.00990099 0.00990099 0.00990099 0.00990099
#> Trackway_18 0.73267327 0.98019802 0.99009901 0.00990099 0.37623762
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0.28712871 1.00000000 1.00000000 0.00990099 0.00990099
#> Trackway_02 0.80198020 1.00000000 1.00000000 0.00990099 0.00990099
#> Trackway_03 0.56435644 1.00000000 1.00000000 0.00990099 0.00990099
#> Trackway_04 0.00990099 1.00000000 0.86138614 0.00990099 0.00990099
#> Trackway_07 0.69306931 1.00000000 1.00000000 0.00990099 0.00990099
#> Trackway_08 NA 1.00000000 1.00000000 0.00990099 0.00990099
#> Trackway_09 1.00000000 NA 1.00000000 0.00990099 1.00000000
#> Trackway_13 1.00000000 1.00000000 NA 0.00990099 1.00000000
#> Trackway_15 0.00990099 0.00990099 0.00990099 NA 0.00990099
#> Trackway_16 0.00990099 1.00000000 1.00000000 0.00990099 NA
#> Trackway_18 0.86138614 1.00000000 1.00000000 0.00990099 0.00990099
#> Trackway_18
#> Trackway_01 0.73267327
#> Trackway_02 0.98019802
#> Trackway_03 0.99009901
#> Trackway_04 0.00990099
#> Trackway_07 0.37623762
#> Trackway_08 0.86138614
#> Trackway_09 1.00000000
#> Trackway_13 1.00000000
#> Trackway_15 0.00990099
#> Trackway_16 0.00990099
#> Trackway_18 NA
#>
#> $DTW_distance_metric_p_values_BH
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0.49720189 0.02475248 1.00000000 1.00000000
#> Trackway_02 0.49720189 NA 1.00000000 1.00000000 1.00000000
#> Trackway_03 0.02475248 1.00000000 NA 0.02475248 1.00000000
#> Trackway_04 1.00000000 1.00000000 0.02475248 NA 0.02475248
#> Trackway_07 1.00000000 1.00000000 1.00000000 0.02475248 NA
#> Trackway_08 0.65800330 1.00000000 1.00000000 0.02475248 1.00000000
#> Trackway_09 1.00000000 1.00000000 1.00000000 1.00000000 1.00000000
#> Trackway_13 1.00000000 1.00000000 1.00000000 1.00000000 1.00000000
#> Trackway_15 0.02475248 0.02475248 0.02475248 0.02475248 0.02475248
#> Trackway_16 0.02475248 0.02475248 0.02475248 0.02475248 0.02475248
#> Trackway_18 1.00000000 1.00000000 1.00000000 0.02475248 0.82772277
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0.65800330 1.00000000 1.00000000 0.02475248 0.02475248
#> Trackway_02 1.00000000 1.00000000 1.00000000 0.02475248 0.02475248
#> Trackway_03 1.00000000 1.00000000 1.00000000 0.02475248 0.02475248
#> Trackway_04 0.02475248 1.00000000 1.00000000 0.02475248 0.02475248
#> Trackway_07 1.00000000 1.00000000 1.00000000 0.02475248 0.02475248
#> Trackway_08 NA 1.00000000 1.00000000 0.02475248 0.02475248
#> Trackway_09 1.00000000 NA 1.00000000 0.02475248 1.00000000
#> Trackway_13 1.00000000 1.00000000 NA 0.02475248 1.00000000
#> Trackway_15 0.02475248 0.02475248 0.02475248 NA 0.02475248
#> Trackway_16 0.02475248 1.00000000 1.00000000 0.02475248 NA
#> Trackway_18 1.00000000 1.00000000 1.00000000 0.02475248 0.02475248
#> Trackway_18
#> Trackway_01 1.00000000
#> Trackway_02 1.00000000
#> Trackway_03 1.00000000
#> Trackway_04 0.02475248
#> Trackway_07 0.82772277
#> Trackway_08 1.00000000
#> Trackway_09 1.00000000
#> Trackway_13 1.00000000
#> Trackway_15 0.02475248
#> Trackway_16 0.02475248
#> Trackway_18 NA
#>
#> $DTW_metric_p_values_combined
#> [1] 0
#>
#> $DTW_distance_metric_simulations
#> $DTW_distance_metric_simulations[[1]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 9.187369 13.396274 5.530992 6.445323
#> Trackway_02 9.187369 NA 4.884035 6.355086 6.243826
#> Trackway_03 13.396274 4.884035 NA 11.975355 3.653586
#> Trackway_04 5.530992 6.355086 11.975355 NA 7.767087
#> Trackway_07 6.445323 6.243826 3.653586 7.767087 NA
#> Trackway_08 9.066059 6.134841 2.708803 9.083288 1.953493
#> Trackway_09 7.787610 5.574484 4.106705 7.155740 2.561692
#> Trackway_13 10.306361 2.390865 2.337244 8.141656 4.065875
#> Trackway_15 42.557728 34.998552 21.273532 45.200024 23.563450
#> Trackway_16 31.983350 26.530403 13.203206 35.284111 13.411377
#> Trackway_18 8.459534 5.991137 2.574782 8.542745 1.527995
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 9.0660592 7.787610 10.306361 42.55773 31.98335
#> Trackway_02 6.1348412 5.574484 2.390865 34.99855 26.53040
#> Trackway_03 2.7088030 4.106705 2.337244 21.27353 13.20321
#> Trackway_04 9.0832879 7.155740 8.141656 45.20002 35.28411
#> Trackway_07 1.9534934 2.561692 4.065875 23.56345 13.41138
#> Trackway_08 NA 2.184863 3.437625 21.64363 11.82494
#> Trackway_09 2.1848632 NA 3.534375 26.96597 17.28305
#> Trackway_13 3.4376254 3.534375 NA 26.89881 18.44097
#> Trackway_15 21.6436331 26.965972 26.898814 NA 14.03359
#> Trackway_16 11.8249378 17.283053 18.440971 14.03359 NA
#> Trackway_18 0.6834821 1.966439 3.185374 22.07819 12.34252
#> Trackway_18
#> Trackway_01 8.4595343
#> Trackway_02 5.9911374
#> Trackway_03 2.5747817
#> Trackway_04 8.5427449
#> Trackway_07 1.5279947
#> Trackway_08 0.6834821
#> Trackway_09 1.9664392
#> Trackway_13 3.1853743
#> Trackway_15 22.0781854
#> Trackway_16 12.3425219
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[2]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 6.862711 15.217277 3.695047 9.227246
#> Trackway_02 6.862711 NA 7.623380 9.530813 4.641496
#> Trackway_03 15.217277 7.623380 NA 18.523296 3.159032
#> Trackway_04 3.695047 9.530813 18.523296 NA 12.314352
#> Trackway_07 9.227246 4.641496 3.159032 12.314352 NA
#> Trackway_08 10.124901 5.234490 2.660464 13.514578 1.117252
#> Trackway_09 7.138671 8.028774 8.527088 8.300780 4.431242
#> Trackway_13 8.640580 3.102516 3.682887 11.738376 1.794842
#> Trackway_15 43.962768 36.140870 20.781186 46.528351 22.336889
#> Trackway_16 32.685749 26.723550 13.202337 35.183541 12.608127
#> Trackway_18 12.645388 5.764721 1.251793 15.988789 1.980149
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 10.124901 7.138671 8.640580 43.96277 32.68575
#> Trackway_02 5.234490 8.028774 3.102516 36.14087 26.72355
#> Trackway_03 2.660464 8.527088 3.682887 20.78119 13.20234
#> Trackway_04 13.514578 8.300780 11.738376 46.52835 35.18354
#> Trackway_07 1.117252 4.431242 1.794842 22.33689 12.60813
#> Trackway_08 NA 4.622570 1.694254 21.32328 11.85814
#> Trackway_09 4.622570 NA 5.363707 28.59530 17.12308
#> Trackway_13 1.694254 5.363707 NA 26.46565 17.26479
#> Trackway_15 21.323279 28.595298 26.465647 NA 14.51792
#> Trackway_16 11.858144 17.123077 17.264794 14.51792 NA
#> Trackway_18 1.553674 6.844458 2.141646 21.23519 12.80204
#> Trackway_18
#> Trackway_01 12.645388
#> Trackway_02 5.764721
#> Trackway_03 1.251793
#> Trackway_04 15.988789
#> Trackway_07 1.980149
#> Trackway_08 1.553674
#> Trackway_09 6.844458
#> Trackway_13 2.141646
#> Trackway_15 21.235191
#> Trackway_16 12.802045
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[3]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 2.963747 16.424815 7.589836 5.826530
#> Trackway_02 2.963747 NA 11.034670 9.977935 3.794308
#> Trackway_03 16.424815 11.034670 NA 22.055493 5.322940
#> Trackway_04 7.589836 9.977935 22.055493 NA 11.111577
#> Trackway_07 5.826530 3.794308 5.322940 11.111577 NA
#> Trackway_08 10.444989 5.878909 3.551279 15.307513 3.043926
#> Trackway_09 8.433319 4.618045 5.218715 14.392430 3.379505
#> Trackway_13 5.478790 2.704518 6.459360 11.161642 2.381441
#> Trackway_15 43.484610 36.595603 19.902396 44.720485 23.405328
#> Trackway_16 33.821854 27.372912 13.680789 33.441234 14.115627
#> Trackway_18 8.917921 5.112900 4.079307 13.199998 2.604961
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 10.4449890 8.433319 5.478790 43.48461 33.82185
#> Trackway_02 5.8789091 4.618045 2.704518 36.59560 27.37291
#> Trackway_03 3.5512794 5.218715 6.459360 19.90240 13.68079
#> Trackway_04 15.3075130 14.392430 11.161642 44.72049 33.44123
#> Trackway_07 3.0439258 3.379505 2.381441 23.40533 14.11563
#> Trackway_08 NA 2.617941 2.955099 20.22691 11.62325
#> Trackway_09 2.6179408 NA 2.766727 27.90795 19.65628
#> Trackway_13 2.9550985 2.766727 NA 26.70998 17.64992
#> Trackway_15 20.2269127 27.907946 26.709979 NA 13.38381
#> Trackway_16 11.6232456 19.656282 17.649920 13.38381 NA
#> Trackway_18 0.7727263 3.127832 2.240048 20.67222 11.70602
#> Trackway_18
#> Trackway_01 8.9179206
#> Trackway_02 5.1129001
#> Trackway_03 4.0793067
#> Trackway_04 13.1999979
#> Trackway_07 2.6049613
#> Trackway_08 0.7727263
#> Trackway_09 3.1278323
#> Trackway_13 2.2400480
#> Trackway_15 20.6722212
#> Trackway_16 11.7060169
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[4]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 3.204397 11.755142 6.066368 5.354684
#> Trackway_02 3.204397 NA 8.287012 7.386542 4.027148
#> Trackway_03 11.755142 8.287012 NA 16.491297 4.190454
#> Trackway_04 6.066368 7.386542 16.491297 NA 8.733268
#> Trackway_07 5.354684 4.027148 4.190454 8.733268 NA
#> Trackway_08 7.538838 5.365387 2.996883 10.929362 2.161076
#> Trackway_09 10.490523 7.804882 1.617819 15.563958 5.255685
#> Trackway_13 11.706444 8.416486 2.503268 17.200311 5.871141
#> Trackway_15 43.687542 38.522048 21.471340 46.939245 25.095273
#> Trackway_16 31.002832 26.242081 11.066897 31.954304 12.404159
#> Trackway_18 8.020840 5.831336 2.963534 10.850873 2.669368
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 7.5388376 10.490523 11.706444 43.68754 31.002832
#> Trackway_02 5.3653874 7.804882 8.416486 38.52205 26.242081
#> Trackway_03 2.9968832 1.617819 2.503268 21.47134 11.066897
#> Trackway_04 10.9293625 15.563958 17.200311 46.93925 31.954304
#> Trackway_07 2.1610760 5.255685 5.871141 25.09527 12.404159
#> Trackway_08 NA 5.091517 5.460329 23.01987 10.398139
#> Trackway_09 5.0915167 NA 2.869762 27.30089 17.027444
#> Trackway_13 5.4603285 2.869762 NA 26.86172 17.385243
#> Trackway_15 23.0198739 27.300891 26.861719 NA 16.509646
#> Trackway_16 10.3981385 17.027444 17.385243 16.50965 NA
#> Trackway_18 0.6053104 5.191516 5.820770 22.60042 9.949348
#> Trackway_18
#> Trackway_01 8.0208395
#> Trackway_02 5.8313360
#> Trackway_03 2.9635343
#> Trackway_04 10.8508728
#> Trackway_07 2.6693675
#> Trackway_08 0.6053104
#> Trackway_09 5.1915160
#> Trackway_13 5.8207705
#> Trackway_15 22.6004194
#> Trackway_16 9.9493478
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[5]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 3.845975 14.232221 5.854210 6.902862
#> Trackway_02 3.845975 NA 8.458270 4.711719 4.106597
#> Trackway_03 14.232221 8.458270 NA 12.371887 4.165945
#> Trackway_04 5.854210 4.711719 12.371887 NA 9.901224
#> Trackway_07 6.902862 4.106597 4.165945 9.901224 NA
#> Trackway_08 15.338739 9.149218 1.493119 13.853840 4.005222
#> Trackway_09 12.014595 6.557922 2.236068 10.517537 5.590088
#> Trackway_13 11.326032 6.098275 2.507950 8.785677 4.493186
#> Trackway_15 43.055056 35.615863 21.903438 45.713393 22.548550
#> Trackway_16 31.826153 25.147002 13.884378 35.288171 12.048814
#> Trackway_18 17.286554 10.811440 1.824687 15.724289 4.940834
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 15.3387393 12.014595 11.326032 43.05506 31.82615
#> Trackway_02 9.1492178 6.557922 6.098275 35.61586 25.14700
#> Trackway_03 1.4931187 2.236068 2.507950 21.90344 13.88438
#> Trackway_04 13.8538402 10.517537 8.785677 45.71339 35.28817
#> Trackway_07 4.0052223 5.590088 4.493186 22.54855 12.04881
#> Trackway_08 NA 2.717072 2.832774 20.70533 12.67692
#> Trackway_09 2.7170724 NA 2.524571 27.38017 18.95243
#> Trackway_13 2.8327742 2.524571 NA 26.50426 17.82820
#> Trackway_15 20.7053251 27.380170 26.504257 NA 13.87823
#> Trackway_16 12.6769243 18.952428 17.828205 13.87823 NA
#> Trackway_18 0.9993497 3.758358 3.870337 20.25282 12.89576
#> Trackway_18
#> Trackway_01 17.2865540
#> Trackway_02 10.8114396
#> Trackway_03 1.8246870
#> Trackway_04 15.7242888
#> Trackway_07 4.9408344
#> Trackway_08 0.9993497
#> Trackway_09 3.7583575
#> Trackway_13 3.8703371
#> Trackway_15 20.2528232
#> Trackway_16 12.8957592
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[6]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 14.442212 19.987081 14.047506 9.546935
#> Trackway_02 14.442212 NA 7.029204 4.657725 6.719124
#> Trackway_03 19.987081 7.029204 NA 13.707917 5.224586
#> Trackway_04 14.047506 4.657725 13.707917 NA 9.193684
#> Trackway_07 9.546935 6.719124 5.224586 9.193684 NA
#> Trackway_08 10.359936 7.167072 4.589887 10.046353 1.795601
#> Trackway_09 14.711235 3.013143 4.063866 8.653524 4.611133
#> Trackway_13 15.824944 2.493656 3.599766 7.113811 4.920092
#> Trackway_15 42.437558 35.296018 20.940017 44.846705 24.014495
#> Trackway_16 30.588815 27.274098 14.209648 36.561798 14.201433
#> Trackway_18 19.068619 6.573928 0.546952 13.197859 4.895519
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 10.359936 14.711235 15.824944 42.43756 30.58881
#> Trackway_02 7.167072 3.013143 2.493656 35.29602 27.27410
#> Trackway_03 4.589887 4.063866 3.599766 20.94002 14.20965
#> Trackway_04 10.046353 8.653524 7.113811 44.84670 36.56180
#> Trackway_07 1.795601 4.611133 4.920092 24.01449 14.20143
#> Trackway_08 NA 4.603846 5.047875 22.25618 12.53214
#> Trackway_09 4.603846 NA 2.309888 28.27739 20.12762
#> Trackway_13 5.047875 2.309888 NA 27.80812 19.96465
#> Trackway_15 22.256181 28.277386 27.808115 NA 13.87814
#> Trackway_16 12.532135 20.127624 19.964654 13.87814 NA
#> Trackway_18 4.140176 3.576900 3.436780 20.81109 13.79381
#> Trackway_18
#> Trackway_01 19.068619
#> Trackway_02 6.573928
#> Trackway_03 0.546952
#> Trackway_04 13.197859
#> Trackway_07 4.895519
#> Trackway_08 4.140176
#> Trackway_09 3.576900
#> Trackway_13 3.436780
#> Trackway_15 20.811094
#> Trackway_16 13.793809
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[7]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 5.113327 13.1771457 5.901685 7.227539
#> Trackway_02 5.113327 NA 7.1968661 4.909546 6.016505
#> Trackway_03 13.177146 7.196866 NA 13.487183 4.689598
#> Trackway_04 5.901685 4.909546 13.4871827 NA 9.347986
#> Trackway_07 7.227539 6.016505 4.6895980 9.347986 NA
#> Trackway_08 9.547036 5.437365 2.2862723 11.364049 3.069833
#> Trackway_09 7.246346 5.497875 5.1337433 10.335455 2.403099
#> Trackway_13 6.732578 2.758404 3.4287847 7.264582 4.134672
#> Trackway_15 43.632791 34.894413 19.8081256 44.931257 22.616918
#> Trackway_16 32.865219 25.361908 11.7709340 35.591147 12.047777
#> Trackway_18 14.476010 8.013968 0.6044453 14.489001 5.207206
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 9.547036 7.246346 6.732578 43.63279 32.86522
#> Trackway_02 5.437365 5.497875 2.758404 34.89441 25.36191
#> Trackway_03 2.286272 5.133743 3.428785 19.80813 11.77093
#> Trackway_04 11.364049 10.335455 7.264582 44.93126 35.59115
#> Trackway_07 3.069833 2.403099 4.134672 22.61692 12.04778
#> Trackway_08 NA 2.534429 3.164343 19.84973 10.39079
#> Trackway_09 2.534429 NA 3.558847 26.18105 15.94973
#> Trackway_13 3.164343 3.558847 NA 26.47135 17.10543
#> Trackway_15 19.849726 26.181046 26.471345 NA 13.11193
#> Trackway_16 10.390788 15.949726 17.105429 13.11193 NA
#> Trackway_18 2.860161 5.958079 4.090273 19.77325 12.11828
#> Trackway_18
#> Trackway_01 14.4760098
#> Trackway_02 8.0139682
#> Trackway_03 0.6044453
#> Trackway_04 14.4890010
#> Trackway_07 5.2072062
#> Trackway_08 2.8601612
#> Trackway_09 5.9580791
#> Trackway_13 4.0902731
#> Trackway_15 19.7732482
#> Trackway_16 12.1182835
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[8]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 8.005978 18.1444540 5.888264 6.455588
#> Trackway_02 8.005978 NA 10.2762521 4.695581 7.762268
#> Trackway_03 18.144454 10.276252 NA 17.383104 6.485602
#> Trackway_04 5.888264 4.695581 17.3831038 NA 10.484924
#> Trackway_07 6.455588 7.762268 6.4856024 10.484924 NA
#> Trackway_08 13.312264 6.241609 2.5078140 12.521358 4.006971
#> Trackway_09 17.003700 9.429197 2.1260047 16.283666 8.902138
#> Trackway_13 8.849324 3.200153 5.5016429 7.108057 4.122979
#> Trackway_15 42.614898 37.549239 21.0528870 46.379676 22.936485
#> Trackway_16 31.031443 27.537837 13.6247250 35.346320 11.779547
#> Trackway_18 18.357910 10.432556 0.9186575 17.633479 6.389960
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 13.312264 17.003700 8.849324 42.61490 31.03144
#> Trackway_02 6.241609 9.429197 3.200153 37.54924 27.53784
#> Trackway_03 2.507814 2.126005 5.501643 21.05289 13.62473
#> Trackway_04 12.521358 16.283666 7.108057 46.37968 35.34632
#> Trackway_07 4.006971 8.902138 4.122979 22.93648 11.77955
#> Trackway_08 NA 3.844661 2.307914 21.36127 12.36388
#> Trackway_09 3.844661 NA 5.608065 26.45448 19.00762
#> Trackway_13 2.307914 5.608065 NA 26.62939 16.71929
#> Trackway_15 21.361272 26.454477 26.629391 NA 13.51075
#> Trackway_16 12.363878 19.007616 16.719294 13.51075 NA
#> Trackway_18 2.426064 2.205207 5.460481 20.36216 12.94404
#> Trackway_18
#> Trackway_01 18.3579103
#> Trackway_02 10.4325562
#> Trackway_03 0.9186575
#> Trackway_04 17.6334794
#> Trackway_07 6.3899603
#> Trackway_08 2.4260639
#> Trackway_09 2.2052073
#> Trackway_13 5.4604808
#> Trackway_15 20.3621573
#> Trackway_16 12.9440381
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[9]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 10.135708 16.543076 6.975391 6.590337
#> Trackway_02 10.135708 NA 7.736503 4.370765 9.336760
#> Trackway_03 16.543076 7.736503 NA 11.924206 5.386271
#> Trackway_04 6.975391 4.370765 11.924206 NA 10.020964
#> Trackway_07 6.590337 9.336760 5.386271 10.020964 NA
#> Trackway_08 14.789770 6.527298 1.615139 10.371693 4.365298
#> Trackway_09 17.559613 8.572872 2.190739 12.206009 8.758206
#> Trackway_13 7.891359 4.580170 4.959965 5.473747 3.465967
#> Trackway_15 44.258419 38.028457 21.372853 43.871781 23.366848
#> Trackway_16 33.375862 29.326122 13.943319 34.127094 12.856835
#> Trackway_18 19.404492 10.039727 1.429479 14.763293 6.341962
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 14.789770 17.559613 7.891359 44.25842 33.37586
#> Trackway_02 6.527298 8.572872 4.580170 38.02846 29.32612
#> Trackway_03 1.615139 2.190739 4.959965 21.37285 13.94332
#> Trackway_04 10.371693 12.206009 5.473747 43.87178 34.12709
#> Trackway_07 4.365298 8.758206 3.465967 23.36685 12.85683
#> Trackway_08 NA 3.390064 3.624383 20.69576 12.50674
#> Trackway_09 3.390064 NA 6.358967 26.14033 19.32328
#> Trackway_13 3.624383 6.358967 NA 26.92374 17.41470
#> Trackway_15 20.695762 26.140333 26.923743 NA 13.46495
#> Trackway_16 12.506742 19.323282 17.414704 13.46495 NA
#> Trackway_18 2.140853 2.201327 6.446300 20.36299 13.59628
#> Trackway_18
#> Trackway_01 19.404492
#> Trackway_02 10.039727
#> Trackway_03 1.429479
#> Trackway_04 14.763293
#> Trackway_07 6.341962
#> Trackway_08 2.140853
#> Trackway_09 2.201327
#> Trackway_13 6.446300
#> Trackway_15 20.362991
#> Trackway_16 13.596278
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[10]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 8.192139 16.985225 3.136036 7.898002
#> Trackway_02 8.192139 NA 7.819659 9.542481 4.736305
#> Trackway_03 16.985225 7.819659 NA 18.996736 4.239722
#> Trackway_04 3.136036 9.542481 18.996736 NA 9.813283
#> Trackway_07 7.898002 4.736305 4.239722 9.813283 NA
#> Trackway_08 8.479128 8.837138 5.760523 10.364092 2.697902
#> Trackway_09 14.231551 5.396669 2.501862 16.040080 5.885192
#> Trackway_13 10.679847 2.889589 3.784906 12.061759 3.461365
#> Trackway_15 44.139522 36.024054 20.960648 47.030205 23.285712
#> Trackway_16 28.222247 23.807046 11.202966 30.959005 10.645390
#> Trackway_18 14.544032 5.928768 1.131828 16.487188 3.162671
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 8.479128 14.231551 10.679847 44.13952 28.222247
#> Trackway_02 8.837138 5.396669 2.889589 36.02405 23.807046
#> Trackway_03 5.760523 2.501862 3.784906 20.96065 11.202966
#> Trackway_04 10.364092 16.040080 12.061759 47.03021 30.959005
#> Trackway_07 2.697902 5.885192 3.461365 23.28571 10.645390
#> Trackway_08 NA 8.658724 6.442011 22.01159 8.285563
#> Trackway_09 8.658724 NA 3.234774 27.71157 17.555570
#> Trackway_13 6.442011 3.234774 NA 27.55130 16.227190
#> Trackway_15 22.011587 27.711572 27.551298 NA 15.669229
#> Trackway_16 8.285563 17.555570 16.227190 15.66923 NA
#> Trackway_18 4.947406 2.213972 2.359802 21.71603 11.152394
#> Trackway_18
#> Trackway_01 14.544032
#> Trackway_02 5.928768
#> Trackway_03 1.131828
#> Trackway_04 16.487188
#> Trackway_07 3.162671
#> Trackway_08 4.947406
#> Trackway_09 2.213972
#> Trackway_13 2.359802
#> Trackway_15 21.716033
#> Trackway_16 11.152394
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[11]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 4.522058 12.388404 5.837063 6.1083878
#> Trackway_02 4.522058 NA 7.085690 3.821806 4.8626875
#> Trackway_03 12.388404 7.085690 NA 11.402467 3.9871843
#> Trackway_04 5.837063 3.821806 11.402467 NA 8.5448397
#> Trackway_07 6.108388 4.862687 3.987184 8.544840 NA
#> Trackway_08 6.836002 5.594269 4.070062 9.786927 0.6618041
#> Trackway_09 8.553785 3.764424 2.927546 8.244786 4.5104493
#> Trackway_13 5.142124 2.992155 4.772614 5.879914 1.8241641
#> Trackway_15 42.187392 34.739797 21.057605 44.526343 22.5496106
#> Trackway_16 30.612202 24.570830 12.797660 34.502853 11.6044907
#> Trackway_18 6.942701 5.482251 3.736882 9.604752 0.8191585
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 6.8360021 8.553785 5.142124 42.18739 30.61220
#> Trackway_02 5.5942691 3.764424 2.992155 34.73980 24.57083
#> Trackway_03 4.0700621 2.927546 4.772614 21.05760 12.79766
#> Trackway_04 9.7869269 8.244786 5.879914 44.52634 34.50285
#> Trackway_07 0.6618041 4.510449 1.824164 22.54961 11.60449
#> Trackway_08 NA 4.671033 2.112791 21.97792 10.94704
#> Trackway_09 4.6710331 NA 3.513479 27.42301 18.26875
#> Trackway_13 2.1127909 3.513479 NA 26.99689 16.44731
#> Trackway_15 21.9779201 27.423014 26.996893 NA 14.65011
#> Trackway_16 10.9470366 18.268752 16.447310 14.65011 NA
#> Trackway_18 0.4732025 4.329697 1.740602 21.85754 11.03941
#> Trackway_18
#> Trackway_01 6.9427014
#> Trackway_02 5.4822511
#> Trackway_03 3.7368820
#> Trackway_04 9.6047520
#> Trackway_07 0.8191585
#> Trackway_08 0.4732025
#> Trackway_09 4.3296970
#> Trackway_13 1.7406017
#> Trackway_15 21.8575419
#> Trackway_16 11.0394078
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[12]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 19.591208 22.230839 20.304183 14.169489
#> Trackway_02 19.59121 NA 5.241607 3.416566 7.183263
#> Trackway_03 22.23084 5.241607 NA 9.013443 3.803165
#> Trackway_04 20.30418 3.416566 9.013443 NA 9.681082
#> Trackway_07 14.16949 7.183263 3.803165 9.681082 NA
#> Trackway_08 12.75373 9.675689 4.831250 13.212705 1.965665
#> Trackway_09 11.80835 9.017314 6.911850 12.939967 2.466075
#> Trackway_13 18.08183 3.880797 3.352349 4.671439 3.140402
#> Trackway_15 44.60371 35.705816 21.943818 44.860065 23.163183
#> Trackway_16 29.35453 26.936173 13.661767 35.705577 12.338286
#> Trackway_18 19.38141 6.074562 2.256291 8.985720 2.732911
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 12.753728 11.808350 18.081834 44.60371 29.35453
#> Trackway_02 9.675689 9.017314 3.880797 35.70582 26.93617
#> Trackway_03 4.831250 6.911850 3.352349 21.94382 13.66177
#> Trackway_04 13.212705 12.939967 4.671439 44.86006 35.70558
#> Trackway_07 1.965665 2.466075 3.140402 23.16318 12.33829
#> Trackway_08 NA 1.678761 4.414012 21.76553 10.40092
#> Trackway_09 1.678761 NA 4.781240 27.79884 16.33552
#> Trackway_13 4.414012 4.781240 NA 26.59774 17.03808
#> Trackway_15 21.765528 27.798841 26.597737 NA 14.95238
#> Trackway_16 10.400920 16.335521 17.038082 14.95238 NA
#> Trackway_18 2.890978 4.863493 2.131491 20.88519 11.53284
#> Trackway_18
#> Trackway_01 19.381405
#> Trackway_02 6.074562
#> Trackway_03 2.256291
#> Trackway_04 8.985720
#> Trackway_07 2.732911
#> Trackway_08 2.890978
#> Trackway_09 4.863493
#> Trackway_13 2.131491
#> Trackway_15 20.885186
#> Trackway_16 11.532838
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[13]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 5.937343 15.154774 2.668076 6.765797
#> Trackway_02 5.937343 NA 8.094923 4.232583 4.427835
#> Trackway_03 15.154774 8.094923 NA 13.761844 4.441043
#> Trackway_04 2.668076 4.232583 13.761844 NA 6.485890
#> Trackway_07 6.765797 4.427835 4.441043 6.485890 NA
#> Trackway_08 8.828028 5.695750 3.625538 8.550262 2.180289
#> Trackway_09 10.307701 4.611327 3.953755 9.245655 3.411146
#> Trackway_13 6.247345 3.613020 5.169105 5.231089 2.140536
#> Trackway_15 44.203863 37.039765 22.038748 44.448268 24.586132
#> Trackway_16 32.008463 26.087264 13.074582 32.574586 13.092266
#> Trackway_18 13.055351 6.613538 1.185672 11.881158 3.488445
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 8.828028 10.307701 6.247345 44.20386 32.00846
#> Trackway_02 5.695750 4.611327 3.613020 37.03977 26.08726
#> Trackway_03 3.625538 3.953755 5.169105 22.03875 13.07458
#> Trackway_04 8.550262 9.245655 5.231089 44.44827 32.57459
#> Trackway_07 2.180289 3.411146 2.140536 24.58613 13.09227
#> Trackway_08 NA 2.963318 1.703440 22.42316 11.18029
#> Trackway_09 2.963318 NA 3.333141 27.58239 17.06160
#> Trackway_13 1.703440 3.333141 NA 27.99560 16.66381
#> Trackway_15 22.423157 27.582387 27.995597 NA 14.66510
#> Trackway_16 11.180291 17.061605 16.663805 14.66510 NA
#> Trackway_18 2.445556 2.680052 3.697912 22.05592 12.33676
#> Trackway_18
#> Trackway_01 13.055351
#> Trackway_02 6.613538
#> Trackway_03 1.185672
#> Trackway_04 11.881158
#> Trackway_07 3.488445
#> Trackway_08 2.445556
#> Trackway_09 2.680052
#> Trackway_13 3.697912
#> Trackway_15 22.055916
#> Trackway_16 12.336762
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[14]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 5.114269 16.5080800 7.218923 9.504735
#> Trackway_02 5.114269 NA 9.8419877 2.910220 4.590420
#> Trackway_03 16.508080 9.841988 NA 12.157608 3.398454
#> Trackway_04 7.218923 2.910220 12.1576082 NA 6.543682
#> Trackway_07 9.504735 4.590420 3.3984538 6.543682 NA
#> Trackway_08 9.642335 5.425364 3.9577437 9.879886 2.149422
#> Trackway_09 9.932172 4.871879 4.6545051 6.775517 2.045878
#> Trackway_13 10.663430 4.953967 3.6011366 5.747614 2.350804
#> Trackway_15 44.432621 36.680283 20.9466591 43.381025 22.910554
#> Trackway_16 32.213980 25.770076 12.5594434 32.866544 12.546963
#> Trackway_18 15.867104 9.354312 0.7321135 11.950417 3.255533
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 9.642335 9.932172 10.663430 44.43262 32.21398
#> Trackway_02 5.425364 4.871879 4.953967 36.68028 25.77008
#> Trackway_03 3.957744 4.654505 3.601137 20.94666 12.55944
#> Trackway_04 9.879886 6.775517 5.747614 43.38103 32.86654
#> Trackway_07 2.149422 2.045878 2.350804 22.91055 12.54696
#> Trackway_08 NA 3.075928 4.178817 21.25424 10.43168
#> Trackway_09 3.075928 NA 2.816400 27.78271 17.56083
#> Trackway_13 4.178817 2.816400 NA 27.22867 17.48540
#> Trackway_15 21.254239 27.782709 27.228667 NA 13.84129
#> Trackway_16 10.431683 17.560827 17.485404 13.84129 NA
#> Trackway_18 3.488779 4.187928 3.525044 20.52936 11.91776
#> Trackway_18
#> Trackway_01 15.8671044
#> Trackway_02 9.3543123
#> Trackway_03 0.7321135
#> Trackway_04 11.9504170
#> Trackway_07 3.2555325
#> Trackway_08 3.4887794
#> Trackway_09 4.1879277
#> Trackway_13 3.5250439
#> Trackway_15 20.5293566
#> Trackway_16 11.9177648
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[15]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 2.992705 7.4229118 7.994620 8.375054
#> Trackway_02 2.992705 NA 6.0941597 6.241451 5.896429
#> Trackway_03 7.422912 6.094160 NA 12.855549 2.956051
#> Trackway_04 7.994620 6.241451 12.8555494 NA 8.412094
#> Trackway_07 8.375054 5.896429 2.9560508 8.412094 NA
#> Trackway_08 11.739419 8.532349 3.8868388 9.627448 1.681190
#> Trackway_09 4.964766 4.372667 1.9359603 10.766807 4.328691
#> Trackway_13 4.640279 3.693262 1.7925453 9.437575 3.417957
#> Trackway_15 40.987857 36.135942 20.9394006 45.348129 22.548759
#> Trackway_16 33.822028 28.220471 13.6730327 36.107435 13.468211
#> Trackway_18 8.056427 5.921769 0.9572341 12.541105 2.813758
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 11.739419 4.964766 4.640279 40.98786 33.82203
#> Trackway_02 8.532349 4.372667 3.693262 36.13594 28.22047
#> Trackway_03 3.886839 1.935960 1.792545 20.93940 13.67303
#> Trackway_04 9.627448 10.766807 9.437575 45.34813 36.10744
#> Trackway_07 1.681190 4.328691 3.417957 22.54876 13.46821
#> Trackway_08 NA 6.040070 4.918507 21.75745 11.99969
#> Trackway_09 6.040070 NA 1.851198 27.17780 19.77531
#> Trackway_13 4.918507 1.851198 NA 25.83977 18.18380
#> Trackway_15 21.757450 27.177802 25.839772 NA 13.71888
#> Trackway_16 11.999687 19.775311 18.183803 13.71888 NA
#> Trackway_18 3.354840 2.380904 1.687783 20.30577 12.73083
#> Trackway_18
#> Trackway_01 8.0564268
#> Trackway_02 5.9217690
#> Trackway_03 0.9572341
#> Trackway_04 12.5411053
#> Trackway_07 2.8137584
#> Trackway_08 3.3548398
#> Trackway_09 2.3809041
#> Trackway_13 1.6877828
#> Trackway_15 20.3057727
#> Trackway_16 12.7308342
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[16]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 3.572518 11.580198 4.621271 6.512345
#> Trackway_02 3.572518 NA 11.123159 6.131658 3.658235
#> Trackway_03 11.580198 11.123159 NA 13.139612 5.186187
#> Trackway_04 4.621271 6.131658 13.139612 NA 9.663862
#> Trackway_07 6.512345 3.658235 5.186187 9.663862 NA
#> Trackway_08 7.105084 6.796868 2.715253 9.515161 2.763853
#> Trackway_09 9.981093 10.191976 2.193831 11.537660 7.753606
#> Trackway_13 4.605469 3.664654 5.731323 6.986909 2.279079
#> Trackway_15 42.560655 37.531365 22.294147 47.348099 24.321498
#> Trackway_16 32.253625 26.887627 14.440283 37.486428 13.753479
#> Trackway_18 13.506367 12.494454 1.451946 15.399294 5.751248
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 7.105084 9.981093 4.605469 42.56065 32.25362
#> Trackway_02 6.796868 10.191976 3.664654 37.53136 26.88763
#> Trackway_03 2.715253 2.193831 5.731323 22.29415 14.44028
#> Trackway_04 9.515161 11.537660 6.986909 47.34810 37.48643
#> Trackway_07 2.763853 7.753606 2.279079 24.32150 13.75348
#> Trackway_08 NA 4.923649 2.354403 22.45785 13.08132
#> Trackway_09 4.923649 NA 6.283726 28.25520 20.41587
#> Trackway_13 2.354403 6.283726 NA 27.23175 17.07127
#> Trackway_15 22.457846 28.255196 27.231749 NA 13.37242
#> Trackway_16 13.081324 20.415873 17.071267 13.37242 NA
#> Trackway_18 3.065512 3.092768 6.334568 20.87643 13.30939
#> Trackway_18
#> Trackway_01 13.506367
#> Trackway_02 12.494454
#> Trackway_03 1.451946
#> Trackway_04 15.399294
#> Trackway_07 5.751248
#> Trackway_08 3.065512
#> Trackway_09 3.092768
#> Trackway_13 6.334568
#> Trackway_15 20.876427
#> Trackway_16 13.309386
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[17]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 6.130006 16.543759 4.506131 9.632925
#> Trackway_02 6.130006 NA 8.879853 2.454377 4.682949
#> Trackway_03 16.543759 8.879853 NA 13.565009 3.690808
#> Trackway_04 4.506131 2.454377 13.565009 NA 7.950453
#> Trackway_07 9.632925 4.682949 3.690808 7.950453 NA
#> Trackway_08 11.364018 5.216176 2.956710 9.330001 1.002614
#> Trackway_09 13.031341 6.056982 3.136967 10.459940 2.926592
#> Trackway_13 10.273952 4.102472 4.210744 7.117733 3.445801
#> Trackway_15 41.777883 34.682384 19.813266 42.153438 19.900833
#> Trackway_16 32.597960 26.495822 13.728814 33.734573 11.852910
#> Trackway_18 14.358510 7.041929 1.572771 11.758943 2.288459
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 11.364018 13.031341 10.273952 41.77788 32.59796
#> Trackway_02 5.216176 6.056982 4.102472 34.68238 26.49582
#> Trackway_03 2.956710 3.136967 4.210744 19.81327 13.72881
#> Trackway_04 9.330001 10.459940 7.117733 42.15344 33.73457
#> Trackway_07 1.002614 2.926592 3.445801 19.90083 11.85291
#> Trackway_08 NA 2.208494 2.483699 19.97660 12.28299
#> Trackway_09 2.208494 NA 3.650059 23.32215 16.12124
#> Trackway_13 2.483699 3.650059 NA 26.23892 18.82894
#> Trackway_15 19.976603 23.322147 26.238918 NA 11.33825
#> Trackway_16 12.282989 16.121244 18.828941 11.33825 NA
#> Trackway_18 1.616602 2.040509 3.450456 19.24091 12.44105
#> Trackway_18
#> Trackway_01 14.358510
#> Trackway_02 7.041929
#> Trackway_03 1.572771
#> Trackway_04 11.758943
#> Trackway_07 2.288459
#> Trackway_08 1.616602
#> Trackway_09 2.040509
#> Trackway_13 3.450456
#> Trackway_15 19.240909
#> Trackway_16 12.441046
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[18]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 4.955040 16.402238 2.352949 6.870986
#> Trackway_02 4.955040 NA 9.731826 4.384121 5.592648
#> Trackway_03 16.402238 9.731826 NA 15.536460 5.326263
#> Trackway_04 2.352949 4.384121 15.536460 NA 6.481233
#> Trackway_07 6.870986 5.592648 5.326263 6.481233 NA
#> Trackway_08 13.846023 7.696573 2.010124 12.853198 3.957416
#> Trackway_09 9.165145 4.398841 4.827554 8.114171 4.407716
#> Trackway_13 7.857621 3.356610 5.069516 7.374554 3.435479
#> Trackway_15 42.988147 35.676959 19.647486 42.714424 22.426591
#> Trackway_16 34.445358 27.951485 14.098113 33.984219 13.831871
#> Trackway_18 12.497539 6.722894 2.602286 11.625531 3.243000
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 13.8460228 9.165145 7.857621 42.98815 34.44536
#> Trackway_02 7.6965727 4.398841 3.356610 35.67696 27.95149
#> Trackway_03 2.0101243 4.827554 5.069516 19.64749 14.09811
#> Trackway_04 12.8531978 8.114171 7.374554 42.71442 33.98422
#> Trackway_07 3.9574159 4.407716 3.435479 22.42659 13.83187
#> Trackway_08 NA 3.125198 3.250697 19.29852 12.58390
#> Trackway_09 3.1251977 NA 2.124167 26.93423 19.68015
#> Trackway_13 3.2506968 2.124167 NA 25.51764 17.96799
#> Trackway_15 19.2985200 26.934230 25.517641 NA 12.42680
#> Trackway_16 12.5839044 19.680153 17.967991 12.42680 NA
#> Trackway_18 0.7461104 2.814354 2.430196 19.73573 12.56304
#> Trackway_18
#> Trackway_01 12.4975393
#> Trackway_02 6.7228939
#> Trackway_03 2.6022856
#> Trackway_04 11.6255315
#> Trackway_07 3.2429995
#> Trackway_08 0.7461104
#> Trackway_09 2.8143539
#> Trackway_13 2.4301962
#> Trackway_15 19.7357287
#> Trackway_16 12.5630361
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[19]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 9.419986 23.504012 20.476280 12.7731286
#> Trackway_02 9.419986 NA 14.505908 11.459182 5.9007183
#> Trackway_03 23.504012 14.505908 NA 10.183156 5.2784432
#> Trackway_04 20.476280 11.459182 10.183156 NA 12.2416464
#> Trackway_07 12.773129 5.900718 5.278443 12.241646 NA
#> Trackway_08 13.907830 5.995106 4.616974 11.201692 0.8045769
#> Trackway_09 14.716832 6.615423 6.454890 8.467617 3.3073752
#> Trackway_13 17.219064 7.825154 4.553334 5.577998 3.8313989
#> Trackway_15 43.328117 38.338086 21.199306 43.378215 21.9207702
#> Trackway_16 30.502013 27.221915 14.160060 35.040232 11.6486825
#> Trackway_18 25.166890 16.166275 1.330347 12.256198 5.8342650
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 13.9078296 14.716832 17.219064 43.32812 30.50201
#> Trackway_02 5.9951063 6.615423 7.825154 38.33809 27.22191
#> Trackway_03 4.6169736 6.454890 4.553334 21.19931 14.16006
#> Trackway_04 11.2016922 8.467617 5.577998 43.37822 35.04023
#> Trackway_07 0.8045769 3.307375 3.831399 21.92077 11.64868
#> Trackway_08 NA 2.467463 3.097487 21.46149 11.60799
#> Trackway_09 2.4674628 NA 2.645729 28.43056 18.77005
#> Trackway_13 3.0974869 2.645729 NA 26.44668 17.48376
#> Trackway_15 21.4614888 28.430563 26.446683 NA 13.58895
#> Trackway_16 11.6079855 18.770048 17.483756 13.58895 NA
#> Trackway_18 5.0780020 7.651106 5.559061 19.95907 13.50405
#> Trackway_18
#> Trackway_01 25.166890
#> Trackway_02 16.166275
#> Trackway_03 1.330347
#> Trackway_04 12.256198
#> Trackway_07 5.834265
#> Trackway_08 5.078002
#> Trackway_09 7.651106
#> Trackway_13 5.559061
#> Trackway_15 19.959068
#> Trackway_16 13.504046
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[20]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 6.004025 18.722710 8.738940 11.470902
#> Trackway_02 6.004025 NA 11.702096 3.764282 6.201409
#> Trackway_03 18.722710 11.702096 NA 14.902181 3.241153
#> Trackway_04 8.738940 3.764282 14.902181 NA 8.361481
#> Trackway_07 11.470902 6.201409 3.241153 8.361481 NA
#> Trackway_08 9.873421 5.754971 3.977966 9.517032 1.489012
#> Trackway_09 9.610022 4.913376 5.649145 8.059114 2.774220
#> Trackway_13 19.817642 12.515146 1.983593 15.524597 6.062406
#> Trackway_15 43.524980 37.479866 20.933515 46.224243 22.388126
#> Trackway_16 32.143528 27.133779 13.268289 36.228406 12.928457
#> Trackway_18 15.146513 8.764181 1.577905 11.173530 1.687291
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 9.873421 9.610022 19.817642 43.52498 32.14353
#> Trackway_02 5.754971 4.913376 12.515146 37.47987 27.13378
#> Trackway_03 3.977966 5.649145 1.983593 20.93351 13.26829
#> Trackway_04 9.517032 8.059114 15.524597 46.22424 36.22841
#> Trackway_07 1.489012 2.774220 6.062406 22.38813 12.92846
#> Trackway_08 NA 2.458557 7.326083 21.52110 11.63223
#> Trackway_09 2.458557 NA 7.035948 27.91494 18.08055
#> Trackway_13 7.326083 7.035948 NA 25.70074 18.89077
#> Trackway_15 21.521105 27.914943 25.700743 NA 12.86024
#> Trackway_16 11.632225 18.080546 18.890769 12.86024 NA
#> Trackway_18 2.566118 3.818073 3.780170 21.58019 13.01033
#> Trackway_18
#> Trackway_01 15.146513
#> Trackway_02 8.764181
#> Trackway_03 1.577905
#> Trackway_04 11.173530
#> Trackway_07 1.687291
#> Trackway_08 2.566118
#> Trackway_09 3.818073
#> Trackway_13 3.780170
#> Trackway_15 21.580193
#> Trackway_16 13.010329
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[21]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 7.253878 16.348847 8.604736 7.904649
#> Trackway_02 7.253878 NA 8.889241 2.951874 8.642072
#> Trackway_03 16.348847 8.889241 NA 13.550754 5.657554
#> Trackway_04 8.604736 2.951874 13.550754 NA 13.678916
#> Trackway_07 7.904649 8.642072 5.657554 13.678916 NA
#> Trackway_08 8.435104 6.061064 3.919751 10.781013 1.824128
#> Trackway_09 7.546816 4.523586 5.975266 8.129003 4.410524
#> Trackway_13 7.460651 2.960649 5.326561 6.448344 4.543007
#> Trackway_15 43.185360 36.537178 20.151368 45.359079 22.455722
#> Trackway_16 32.267888 27.332237 12.800588 36.506708 11.377799
#> Trackway_18 18.994019 11.174961 1.292918 16.061386 6.934557
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 8.435104 7.546816 7.460651 43.18536 32.26789
#> Trackway_02 6.061064 4.523586 2.960649 36.53718 27.33224
#> Trackway_03 3.919751 5.975266 5.326561 20.15137 12.80059
#> Trackway_04 10.781013 8.129003 6.448344 45.35908 36.50671
#> Trackway_07 1.824128 4.410524 4.543007 22.45572 11.37780
#> Trackway_08 NA 2.606533 2.481338 21.95486 11.93206
#> Trackway_09 2.606533 NA 2.489289 27.74810 18.13600
#> Trackway_13 2.481338 2.489289 NA 27.54993 18.03330
#> Trackway_15 21.954863 27.748104 27.549927 NA 14.12637
#> Trackway_16 11.932059 18.135999 18.033295 14.12637 NA
#> Trackway_18 5.199613 7.701405 6.992046 19.65431 13.29140
#> Trackway_18
#> Trackway_01 18.994019
#> Trackway_02 11.174961
#> Trackway_03 1.292918
#> Trackway_04 16.061386
#> Trackway_07 6.934557
#> Trackway_08 5.199613
#> Trackway_09 7.701405
#> Trackway_13 6.992046
#> Trackway_15 19.654306
#> Trackway_16 13.291400
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[22]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 3.479576 15.691464 12.280886 6.385295
#> Trackway_02 3.479576 NA 10.616500 9.588555 5.022007
#> Trackway_03 15.691464 10.616500 NA 11.224209 4.809532
#> Trackway_04 12.280886 9.588555 11.224209 NA 14.426621
#> Trackway_07 6.385295 5.022007 4.809532 14.426621 NA
#> Trackway_08 9.545323 6.104670 3.976932 14.083861 1.761963
#> Trackway_09 13.902719 8.960478 2.540730 7.835192 7.734936
#> Trackway_13 7.293691 4.173141 4.650768 9.504503 3.128402
#> Trackway_15 45.183626 38.983476 22.443185 47.930252 24.413894
#> Trackway_16 33.082448 27.406207 13.729187 38.585037 12.600868
#> Trackway_18 14.276200 9.606424 0.933988 10.773219 4.246739
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 9.545323 13.902719 7.293691 45.18363 33.08245
#> Trackway_02 6.104670 8.960478 4.173141 38.98348 27.40621
#> Trackway_03 3.976932 2.540730 4.650768 22.44318 13.72919
#> Trackway_04 14.083861 7.835192 9.504503 47.93025 38.58504
#> Trackway_07 1.761963 7.734936 3.128402 24.41389 12.60087
#> Trackway_08 NA 6.537570 3.040271 22.76309 11.40509
#> Trackway_09 6.537570 NA 4.970325 30.07707 21.38556
#> Trackway_13 3.040271 4.970325 NA 28.46964 17.61688
#> Trackway_15 22.763094 30.077068 28.469644 NA 15.43824
#> Trackway_16 11.405091 21.385562 17.616876 15.43824 NA
#> Trackway_18 3.416643 2.885472 3.753665 22.60470 13.49121
#> Trackway_18
#> Trackway_01 14.276200
#> Trackway_02 9.606424
#> Trackway_03 0.933988
#> Trackway_04 10.773219
#> Trackway_07 4.246739
#> Trackway_08 3.416643
#> Trackway_09 2.885472
#> Trackway_13 3.753665
#> Trackway_15 22.604698
#> Trackway_16 13.491210
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[23]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 3.162741 16.1693667 5.776717 8.091271
#> Trackway_02 3.162741 NA 13.1717321 6.665239 6.172684
#> Trackway_03 16.169367 13.171732 NA 13.140205 3.789404
#> Trackway_04 5.776717 6.665239 13.1402046 NA 6.554334
#> Trackway_07 8.091271 6.172684 3.7894044 6.554334 NA
#> Trackway_08 8.685301 5.686147 4.0765070 8.992404 2.058529
#> Trackway_09 10.954208 8.806023 3.9139158 7.899136 2.709491
#> Trackway_13 7.805963 6.366800 4.8588261 5.051352 1.772198
#> Trackway_15 42.121304 37.301559 19.8516751 42.305884 22.401120
#> Trackway_16 29.137618 24.537091 11.8239235 31.644836 11.697525
#> Trackway_18 15.811758 12.716509 0.4920941 12.857788 3.419863
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 8.685301 10.954208 7.805963 42.12130 29.137618
#> Trackway_02 5.686147 8.806023 6.366800 37.30156 24.537091
#> Trackway_03 4.076507 3.913916 4.858826 19.85168 11.823923
#> Trackway_04 8.992404 7.899136 5.051352 42.30588 31.644836
#> Trackway_07 2.058529 2.709491 1.772198 22.40112 11.697525
#> Trackway_08 NA 3.924602 3.266318 20.86237 9.671248
#> Trackway_09 3.924602 NA 2.409757 26.84784 17.215847
#> Trackway_13 3.266318 2.409757 NA 26.63709 16.215789
#> Trackway_15 20.862366 26.847840 26.637087 NA 15.150087
#> Trackway_16 9.671248 17.215847 16.215789 15.15009 NA
#> Trackway_18 3.707979 3.591762 4.537724 19.99415 11.643750
#> Trackway_18
#> Trackway_01 15.8117580
#> Trackway_02 12.7165085
#> Trackway_03 0.4920941
#> Trackway_04 12.8577883
#> Trackway_07 3.4198627
#> Trackway_08 3.7079785
#> Trackway_09 3.5917617
#> Trackway_13 4.5377241
#> Trackway_15 19.9941537
#> Trackway_16 11.6437496
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[24]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 2.950488 15.125458 2.316519 7.712631
#> Trackway_02 2.950488 NA 10.021663 2.392284 4.464802
#> Trackway_03 15.125458 10.021663 NA 14.603893 4.192813
#> Trackway_04 2.316519 2.392284 14.603893 NA 8.056773
#> Trackway_07 7.712631 4.464802 4.192813 8.056773 NA
#> Trackway_08 8.267911 6.305140 5.268072 9.712951 1.824935
#> Trackway_09 13.947257 9.132409 1.830639 13.412821 6.073247
#> Trackway_13 6.118230 5.342728 8.423052 7.983206 3.119975
#> Trackway_15 44.233244 37.129090 21.378763 45.225877 22.924040
#> Trackway_16 32.839763 26.100064 13.177630 34.284929 11.904379
#> Trackway_18 9.639336 5.468407 2.875938 9.523425 1.350070
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 8.267911 13.947257 6.118230 44.23324 32.83976
#> Trackway_02 6.305140 9.132409 5.342728 37.12909 26.10006
#> Trackway_03 5.268072 1.830639 8.423052 21.37876 13.17763
#> Trackway_04 9.712951 13.412821 7.983206 45.22588 34.28493
#> Trackway_07 1.824935 6.073247 3.119975 22.92404 11.90438
#> Trackway_08 NA 7.622723 2.788313 21.97496 10.29717
#> Trackway_09 7.622723 NA 8.726318 26.63431 18.54706
#> Trackway_13 2.788313 8.726318 NA 28.59482 16.36618
#> Trackway_15 21.974964 26.634311 28.594817 NA 14.84213
#> Trackway_16 10.297167 18.547055 16.366177 14.84213 NA
#> Trackway_18 2.590835 4.349590 4.731263 22.23291 12.03521
#> Trackway_18
#> Trackway_01 9.639336
#> Trackway_02 5.468407
#> Trackway_03 2.875938
#> Trackway_04 9.523425
#> Trackway_07 1.350070
#> Trackway_08 2.590835
#> Trackway_09 4.349590
#> Trackway_13 4.731263
#> Trackway_15 22.232907
#> Trackway_16 12.035207
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[25]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 12.163622 18.203123 3.823303 6.599540
#> Trackway_02 12.163622 NA 7.730917 9.531102 9.137839
#> Trackway_03 18.203123 7.730917 NA 16.610462 5.674712
#> Trackway_04 3.823303 9.531102 16.610462 NA 7.695416
#> Trackway_07 6.599540 9.137839 5.674712 7.695416 NA
#> Trackway_08 11.801996 6.204465 2.829541 10.582503 2.875794
#> Trackway_09 21.639006 10.394691 3.461069 20.120108 10.244046
#> Trackway_13 11.676344 3.191546 3.598391 9.464581 4.587840
#> Trackway_15 45.394368 38.098419 21.327862 46.422719 24.856924
#> Trackway_16 27.709688 25.784254 10.607074 30.071714 10.439220
#> Trackway_18 13.730651 5.585701 2.106114 12.451662 3.591327
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 11.8019957 21.639006 11.676344 45.39437 27.70969
#> Trackway_02 6.2044648 10.394691 3.191546 38.09842 25.78425
#> Trackway_03 2.8295413 3.461069 3.598391 21.32786 10.60707
#> Trackway_04 10.5825025 20.120108 9.464581 46.42272 30.07171
#> Trackway_07 2.8757943 10.244046 4.587840 24.85692 10.43922
#> Trackway_08 NA 7.099738 1.902083 22.74339 9.84504
#> Trackway_09 7.0997376 NA 6.548760 25.72277 16.84029
#> Trackway_13 1.9020832 6.548760 NA 27.17870 14.66972
#> Trackway_15 22.7433950 25.722772 27.178696 NA 16.63768
#> Trackway_16 9.8450404 16.840291 14.669725 16.63768 NA
#> Trackway_18 0.9693445 6.052835 1.598469 22.66930 10.36859
#> Trackway_18
#> Trackway_01 13.7306505
#> Trackway_02 5.5857006
#> Trackway_03 2.1061142
#> Trackway_04 12.4516623
#> Trackway_07 3.5913265
#> Trackway_08 0.9693445
#> Trackway_09 6.0528348
#> Trackway_13 1.5984695
#> Trackway_15 22.6692963
#> Trackway_16 10.3685900
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[26]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 7.320864 8.9833885 3.544028 12.374682
#> Trackway_02 7.320864 NA 9.5304866 6.001407 5.193286
#> Trackway_03 8.983389 9.530487 NA 12.097381 4.991902
#> Trackway_04 3.544028 6.001407 12.0973812 NA 11.642776
#> Trackway_07 12.374682 5.193286 4.9919015 11.642776 NA
#> Trackway_08 9.727519 6.054045 3.0159433 9.678160 2.153059
#> Trackway_09 12.145676 5.197943 7.2667914 11.945121 1.888070
#> Trackway_13 5.295931 7.083983 2.1117817 7.861680 5.836633
#> Trackway_15 43.310993 36.967206 21.3530871 45.748770 23.765855
#> Trackway_16 34.186901 25.716582 12.9249212 36.068264 11.925150
#> Trackway_18 8.397022 8.311089 0.8660092 10.913137 4.280330
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 9.727519 12.145676 5.295931 43.31099 34.18690
#> Trackway_02 6.054045 5.197943 7.083983 36.96721 25.71658
#> Trackway_03 3.015943 7.266791 2.111782 21.35309 12.92492
#> Trackway_04 9.678160 11.945121 7.861680 45.74877 36.06826
#> Trackway_07 2.153059 1.888070 5.836633 23.76585 11.92515
#> Trackway_08 NA 3.309389 3.269349 22.12085 11.46984
#> Trackway_09 3.309389 NA 6.142223 28.49435 16.57637
#> Trackway_13 3.269349 6.142223 NA 26.31321 17.37106
#> Trackway_15 22.120845 28.494348 26.313209 NA 15.47380
#> Trackway_16 11.469844 16.576366 17.371058 15.47380 NA
#> Trackway_18 2.241185 6.284433 1.443074 21.33014 12.33224
#> Trackway_18
#> Trackway_01 8.3970217
#> Trackway_02 8.3110890
#> Trackway_03 0.8660092
#> Trackway_04 10.9131368
#> Trackway_07 4.2803303
#> Trackway_08 2.2411852
#> Trackway_09 6.2844329
#> Trackway_13 1.4430737
#> Trackway_15 21.3301449
#> Trackway_16 12.3322364
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[27]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 2.472449 13.587278 5.175909 7.2121907
#> Trackway_02 2.472449 NA 11.012118 4.390502 5.5563925
#> Trackway_03 13.587278 11.012118 NA 13.679774 3.7699518
#> Trackway_04 5.175909 4.390502 13.679774 NA 9.5088249
#> Trackway_07 7.212191 5.556393 3.769952 9.508825 NA
#> Trackway_08 7.874385 5.990716 3.511829 9.766273 0.6595516
#> Trackway_09 11.839604 9.418100 2.306407 11.677104 5.4015019
#> Trackway_13 6.206071 4.703327 4.627044 5.971983 1.9449438
#> Trackway_15 42.609324 37.790765 22.026265 47.041855 22.2253175
#> Trackway_16 31.099124 26.438962 13.635272 36.030020 11.5428783
#> Trackway_18 15.011488 12.192596 1.558818 15.451087 3.8347657
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 7.8743848 11.839604 6.206071 42.60932 31.09912
#> Trackway_02 5.9907157 9.418100 4.703327 37.79077 26.43896
#> Trackway_03 3.5118295 2.306407 4.627044 22.02626 13.63527
#> Trackway_04 9.7662730 11.677104 5.971983 47.04185 36.03002
#> Trackway_07 0.6595516 5.401502 1.944944 22.22532 11.54288
#> Trackway_08 NA 5.236897 1.962723 21.99766 11.48758
#> Trackway_09 5.2368967 NA 4.529735 28.40977 19.79496
#> Trackway_13 1.9627235 4.529735 NA 27.58054 17.24149
#> Trackway_15 21.9976606 28.409766 27.580539 NA 14.28900
#> Trackway_16 11.4875811 19.794960 17.241490 14.28900 NA
#> Trackway_18 3.5369243 2.713739 5.268253 20.49740 12.35536
#> Trackway_18
#> Trackway_01 15.011488
#> Trackway_02 12.192596
#> Trackway_03 1.558818
#> Trackway_04 15.451087
#> Trackway_07 3.834766
#> Trackway_08 3.536924
#> Trackway_09 2.713739
#> Trackway_13 5.268253
#> Trackway_15 20.497399
#> Trackway_16 12.355360
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[28]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 7.094400 17.0131176 5.781565 5.890225
#> Trackway_02 7.094400 NA 9.6891364 3.523966 5.990409
#> Trackway_03 17.013118 9.689136 NA 15.233454 5.798457
#> Trackway_04 5.781565 3.523966 15.2334542 NA 7.739836
#> Trackway_07 5.890225 5.990409 5.7984566 7.739836 NA
#> Trackway_08 6.698805 8.133486 6.1092265 10.359035 1.545656
#> Trackway_09 10.528805 5.170200 4.5722051 9.400041 4.929126
#> Trackway_13 9.499605 3.753541 4.6750014 7.471554 3.912957
#> Trackway_15 42.360679 37.012248 20.3958108 44.135883 23.641350
#> Trackway_16 32.227085 28.031027 13.4500655 35.218767 13.851991
#> Trackway_18 16.241522 9.053065 0.4883435 14.427074 5.469165
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 6.698805 10.528805 9.499605 42.36068 32.22708
#> Trackway_02 8.133486 5.170200 3.753541 37.01225 28.03103
#> Trackway_03 6.109226 4.572205 4.675001 20.39581 13.45007
#> Trackway_04 10.359035 9.400041 7.471554 44.13588 35.21877
#> Trackway_07 1.545656 4.929126 3.912957 23.64135 13.85199
#> Trackway_08 NA 5.961402 4.950128 22.64563 12.50569
#> Trackway_09 5.961402 NA 2.273227 27.16837 18.80395
#> Trackway_13 4.950128 2.273227 NA 26.78223 18.25165
#> Trackway_15 22.645630 27.168366 26.782230 NA 12.38059
#> Trackway_16 12.505694 18.803955 18.251653 12.38059 NA
#> Trackway_18 5.849775 4.248547 4.187699 20.77865 13.66628
#> Trackway_18
#> Trackway_01 16.2415223
#> Trackway_02 9.0530654
#> Trackway_03 0.4883435
#> Trackway_04 14.4270735
#> Trackway_07 5.4691650
#> Trackway_08 5.8497749
#> Trackway_09 4.2485472
#> Trackway_13 4.1876986
#> Trackway_15 20.7786521
#> Trackway_16 13.6662822
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[29]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 5.515664 13.511131 7.065352 6.572452
#> Trackway_02 5.515664 NA 7.784207 2.554528 6.045044
#> Trackway_03 13.511131 7.784207 NA 10.720757 4.162414
#> Trackway_04 7.065352 2.554528 10.720757 NA 9.559877
#> Trackway_07 6.572452 6.045044 4.162414 9.559877 NA
#> Trackway_08 8.214689 5.057700 2.968336 8.292664 1.226804
#> Trackway_09 5.393493 5.981420 7.084255 9.524441 1.783489
#> Trackway_13 9.468649 4.150329 2.390948 6.515432 4.246294
#> Trackway_15 43.164635 36.920333 21.299781 43.755457 22.946134
#> Trackway_16 31.861377 27.041769 13.066940 34.736694 11.896029
#> Trackway_18 11.684967 6.327803 1.123029 9.697158 3.151614
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 8.214689 5.393493 9.468649 43.16463 31.86138
#> Trackway_02 5.057700 5.981420 4.150329 36.92033 27.04177
#> Trackway_03 2.968336 7.084255 2.390948 21.29978 13.06694
#> Trackway_04 8.292664 9.524441 6.515432 43.75546 34.73669
#> Trackway_07 1.226804 1.783489 4.246294 22.94613 11.89603
#> Trackway_08 NA 3.086842 2.764420 22.50157 12.20381
#> Trackway_09 3.086842 NA 5.104775 28.71884 17.45557
#> Trackway_13 2.764420 5.104775 NA 25.98601 16.88802
#> Trackway_15 22.501565 28.718843 25.986006 NA 14.90319
#> Trackway_16 12.203813 17.455571 16.888015 14.90319 NA
#> Trackway_18 2.005839 5.548417 1.320881 21.25450 12.27308
#> Trackway_18
#> Trackway_01 11.684967
#> Trackway_02 6.327803
#> Trackway_03 1.123029
#> Trackway_04 9.697158
#> Trackway_07 3.151614
#> Trackway_08 2.005839
#> Trackway_09 5.548417
#> Trackway_13 1.320881
#> Trackway_15 21.254498
#> Trackway_16 12.273083
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[30]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 7.154087 15.421039 11.302156 7.456817
#> Trackway_02 7.154087 NA 7.326361 5.675580 7.022475
#> Trackway_03 15.421039 7.326361 NA 10.908465 4.661310
#> Trackway_04 11.302156 5.675580 10.908465 NA 14.163816
#> Trackway_07 7.456817 7.022475 4.661310 14.163816 NA
#> Trackway_08 11.594659 5.292011 1.942641 10.191760 2.742867
#> Trackway_09 13.863693 5.745003 2.305460 9.067772 7.179278
#> Trackway_13 9.634046 2.958629 4.324328 5.871221 5.170783
#> Trackway_15 43.763691 35.239215 19.873590 44.652333 22.246871
#> Trackway_16 33.685871 26.858814 12.841943 37.492912 12.326686
#> Trackway_18 8.571639 5.598801 3.289192 12.123592 1.426157
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 11.594659 13.863693 9.634046 43.76369 33.68587
#> Trackway_02 5.292011 5.745003 2.958629 35.23921 26.85881
#> Trackway_03 1.942641 2.305460 4.324328 19.87359 12.84194
#> Trackway_04 10.191760 9.067772 5.871221 44.65233 37.49291
#> Trackway_07 2.742867 7.179278 5.170783 22.24687 12.32669
#> Trackway_08 NA 3.484515 3.476967 20.62810 12.28305
#> Trackway_09 3.484515 NA 3.757069 26.66407 19.88396
#> Trackway_13 3.476967 3.757069 NA 27.59442 19.61787
#> Trackway_15 20.628104 26.664071 27.594424 NA 13.44630
#> Trackway_16 12.283055 19.883965 19.617867 13.44630 NA
#> Trackway_18 1.398100 5.453897 3.915225 21.48757 12.35569
#> Trackway_18
#> Trackway_01 8.571639
#> Trackway_02 5.598801
#> Trackway_03 3.289192
#> Trackway_04 12.123592
#> Trackway_07 1.426157
#> Trackway_08 1.398100
#> Trackway_09 5.453897
#> Trackway_13 3.915225
#> Trackway_15 21.487572
#> Trackway_16 12.355686
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[31]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 4.540646 9.781910 8.534517 6.845039
#> Trackway_02 4.540646 NA 6.319492 7.247235 5.054665
#> Trackway_03 9.781910 6.319492 NA 13.781448 4.084046
#> Trackway_04 8.534517 7.247235 13.781448 NA 6.845376
#> Trackway_07 6.845039 5.054665 4.084046 6.845376 NA
#> Trackway_08 8.789787 5.533532 1.000123 12.407847 3.197932
#> Trackway_09 9.535070 7.331469 7.733091 6.344312 3.319156
#> Trackway_13 5.491463 2.919371 3.270779 10.044615 3.663580
#> Trackway_15 40.354575 34.731486 20.284790 43.453975 23.538702
#> Trackway_16 32.481236 25.970155 12.492203 32.751316 13.606221
#> Trackway_18 7.747582 4.610568 1.789815 10.522929 2.445578
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 8.7897865 9.535070 5.491463 40.35458 32.48124
#> Trackway_02 5.5335315 7.331469 2.919371 34.73149 25.97016
#> Trackway_03 1.0001233 7.733091 3.270779 20.28479 12.49220
#> Trackway_04 12.4078472 6.344312 10.044615 43.45397 32.75132
#> Trackway_07 3.1979316 3.319156 3.663580 23.53870 13.60622
#> Trackway_08 NA 6.482748 2.727387 20.79558 12.34495
#> Trackway_09 6.4827483 NA 6.664416 28.53604 17.57301
#> Trackway_13 2.7273874 6.664416 NA 27.31341 18.95225
#> Trackway_15 20.7955767 28.536038 27.313413 NA 13.92592
#> Trackway_16 12.3449499 17.573007 18.952249 13.92592 NA
#> Trackway_18 0.8471441 5.309367 2.591455 21.28449 12.29540
#> Trackway_18
#> Trackway_01 7.7475823
#> Trackway_02 4.6105679
#> Trackway_03 1.7898153
#> Trackway_04 10.5229290
#> Trackway_07 2.4455782
#> Trackway_08 0.8471441
#> Trackway_09 5.3093674
#> Trackway_13 2.5914554
#> Trackway_15 21.2844945
#> Trackway_16 12.2953984
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[32]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 4.968477 15.8892982 7.985243 7.406004
#> Trackway_02 4.968477 NA 10.0667264 11.268742 5.426593
#> Trackway_03 15.889298 10.066726 NA 21.460112 4.644905
#> Trackway_04 7.985243 11.268742 21.4601117 NA 11.080721
#> Trackway_07 7.406004 5.426593 4.6449052 11.080721 NA
#> Trackway_08 8.457521 6.058630 4.4923194 10.828730 1.188102
#> Trackway_09 5.707013 5.987733 8.1428291 8.929799 2.185211
#> Trackway_13 6.782449 2.756162 5.4540752 12.635208 2.449094
#> Trackway_15 42.018947 36.697253 19.7792385 44.301987 21.638303
#> Trackway_16 33.227793 28.442742 13.6759047 33.796038 12.955530
#> Trackway_18 14.934484 9.156485 0.8998597 20.151497 4.005502
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 8.457521 5.707013 6.782449 42.01895 33.22779
#> Trackway_02 6.058630 5.987733 2.756162 36.69725 28.44274
#> Trackway_03 4.492319 8.142829 5.454075 19.77924 13.67590
#> Trackway_04 10.828730 8.929799 12.635208 44.30199 33.79604
#> Trackway_07 1.188102 2.185211 2.449094 21.63830 12.95553
#> Trackway_08 NA 2.152194 3.173841 20.53403 11.84865
#> Trackway_09 2.152194 NA 3.839362 27.64077 18.58361
#> Trackway_13 3.173841 3.839362 NA 26.60948 18.59742
#> Trackway_15 20.534027 27.640769 26.609480 NA 11.93518
#> Trackway_16 11.848646 18.583606 18.597419 11.93518 NA
#> Trackway_18 3.714852 7.230117 4.783280 19.45288 12.92217
#> Trackway_18
#> Trackway_01 14.9344838
#> Trackway_02 9.1564851
#> Trackway_03 0.8998597
#> Trackway_04 20.1514975
#> Trackway_07 4.0055019
#> Trackway_08 3.7148517
#> Trackway_09 7.2301166
#> Trackway_13 4.7832804
#> Trackway_15 19.4528828
#> Trackway_16 12.9221722
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[33]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 15.837237 19.954670 15.654050 11.227729
#> Trackway_02 15.83724 NA 6.996308 2.405122 7.016207
#> Trackway_03 19.95467 6.996308 NA 10.006923 4.170151
#> Trackway_04 15.65405 2.405122 10.006923 NA 8.095774
#> Trackway_07 11.22773 7.016207 4.170151 8.095774 NA
#> Trackway_08 8.94210 11.197948 5.333947 13.486589 2.307835
#> Trackway_09 12.16631 6.238808 5.341912 7.703802 1.985774
#> Trackway_13 16.01186 3.186138 2.897341 4.873863 3.823752
#> Trackway_15 44.03836 38.088074 22.109640 44.042360 24.196850
#> Trackway_16 28.11007 27.207107 12.356087 33.049761 11.747534
#> Trackway_18 14.74192 5.954578 2.437809 8.133941 1.908652
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 8.942100 12.166311 16.011861 44.03836 28.110073
#> Trackway_02 11.197948 6.238808 3.186138 38.08807 27.207107
#> Trackway_03 5.333947 5.341912 2.897341 22.10964 12.356087
#> Trackway_04 13.486589 7.703802 4.873863 44.04236 33.049761
#> Trackway_07 2.307835 1.985774 3.823752 24.19685 11.747534
#> Trackway_08 NA 3.996902 6.032502 22.94649 9.675891
#> Trackway_09 3.996902 NA 3.348190 28.56936 16.408449
#> Trackway_13 6.032502 3.348190 NA 27.58292 16.648909
#> Trackway_15 22.946486 28.569362 27.582918 NA 15.757747
#> Trackway_16 9.675891 16.408449 16.648909 15.75775 NA
#> Trackway_18 2.974419 2.172669 2.144792 22.76556 11.284582
#> Trackway_18
#> Trackway_01 14.741924
#> Trackway_02 5.954578
#> Trackway_03 2.437809
#> Trackway_04 8.133941
#> Trackway_07 1.908652
#> Trackway_08 2.974419
#> Trackway_09 2.172669
#> Trackway_13 2.144792
#> Trackway_15 22.765565
#> Trackway_16 11.284582
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[34]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 4.200481 10.969534 7.524685 6.711260
#> Trackway_02 4.200481 NA 7.248312 5.592976 6.161610
#> Trackway_03 10.969534 7.248312 NA 8.800236 3.695888
#> Trackway_04 7.524685 5.592976 8.800236 NA 11.911243
#> Trackway_07 6.711260 6.161610 3.695888 11.911243 NA
#> Trackway_08 7.762657 5.236471 2.023620 9.500833 1.716258
#> Trackway_09 5.906935 3.893370 4.642623 9.327723 2.611953
#> Trackway_13 9.934643 6.743650 2.768053 5.304029 6.613033
#> Trackway_15 40.359757 35.572216 19.732999 42.227553 21.734931
#> Trackway_16 30.761943 25.844952 11.538338 34.182014 11.059715
#> Trackway_18 14.268508 10.291627 1.747442 11.299087 5.289402
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 7.762657 5.906935 9.934643 40.35976 30.76194
#> Trackway_02 5.236471 3.893370 6.743650 35.57222 25.84495
#> Trackway_03 2.023620 4.642623 2.768053 19.73300 11.53834
#> Trackway_04 9.500833 9.327723 5.304029 42.22755 34.18201
#> Trackway_07 1.716258 2.611953 6.613033 21.73493 11.05972
#> Trackway_08 NA 2.288295 4.630925 20.78175 11.14456
#> Trackway_09 2.288295 NA 5.804218 28.31022 18.03336
#> Trackway_13 4.630925 5.804218 NA 25.87569 18.29968
#> Trackway_15 20.781754 28.310219 25.875695 NA 14.22491
#> Trackway_16 11.144563 18.033364 18.299681 14.22491 NA
#> Trackway_18 3.634786 7.090053 3.226777 19.36344 12.45321
#> Trackway_18
#> Trackway_01 14.268508
#> Trackway_02 10.291627
#> Trackway_03 1.747442
#> Trackway_04 11.299087
#> Trackway_07 5.289402
#> Trackway_08 3.634786
#> Trackway_09 7.090053
#> Trackway_13 3.226777
#> Trackway_15 19.363443
#> Trackway_16 12.453215
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[35]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 11.363943 17.892384 6.827127 12.416608
#> Trackway_02 11.363943 NA 7.259892 7.011191 4.449618
#> Trackway_03 17.892384 7.259892 NA 15.616707 2.664694
#> Trackway_04 6.827127 7.011191 15.616707 NA 10.716845
#> Trackway_07 12.416608 4.449618 2.664694 10.716845 NA
#> Trackway_08 11.232426 5.672713 3.350747 9.968517 1.280778
#> Trackway_09 12.665547 3.910282 3.648195 10.544076 2.298449
#> Trackway_13 11.856626 3.312070 3.618694 8.685669 1.820162
#> Trackway_15 44.054031 36.395122 21.394201 46.760145 22.700618
#> Trackway_16 29.740048 26.008900 12.648510 34.466012 12.046503
#> Trackway_18 15.000072 5.592931 1.448911 12.979340 1.445299
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 11.232426 12.665547 11.856626 44.05403 29.74005
#> Trackway_02 5.672713 3.910282 3.312070 36.39512 26.00890
#> Trackway_03 3.350747 3.648195 3.618694 21.39420 12.64851
#> Trackway_04 9.968517 10.544076 8.685669 46.76014 34.46601
#> Trackway_07 1.280778 2.298449 1.820162 22.70062 12.04650
#> Trackway_08 NA 3.298301 2.068897 22.00759 10.83320
#> Trackway_09 3.298301 NA 1.662153 27.70320 17.56175
#> Trackway_13 2.068897 1.662153 NA 26.31579 15.80046
#> Trackway_15 22.007590 27.703202 26.315793 NA 15.48831
#> Trackway_16 10.833202 17.561748 15.800463 15.48831 NA
#> Trackway_18 1.932080 2.183929 1.876047 21.56689 11.76552
#> Trackway_18
#> Trackway_01 15.000072
#> Trackway_02 5.592931
#> Trackway_03 1.448911
#> Trackway_04 12.979340
#> Trackway_07 1.445299
#> Trackway_08 1.932080
#> Trackway_09 2.183929
#> Trackway_13 1.876047
#> Trackway_15 21.566890
#> Trackway_16 11.765518
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[36]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 10.118613 13.429558 2.537744 8.135770
#> Trackway_02 10.118613 NA 4.377065 8.402016 7.466026
#> Trackway_03 13.429558 4.377065 NA 12.264568 3.233265
#> Trackway_04 2.537744 8.402016 12.264568 NA 8.210375
#> Trackway_07 8.135770 7.466026 3.233265 8.210375 NA
#> Trackway_08 10.291318 6.267952 2.281460 9.461518 1.324704
#> Trackway_09 17.549136 6.896639 4.130870 16.510590 8.337072
#> Trackway_13 9.868233 2.785510 2.497061 8.592397 3.298160
#> Trackway_15 43.205446 35.099459 20.569236 44.337234 21.615628
#> Trackway_16 28.574266 24.813431 11.004872 30.531294 9.905416
#> Trackway_18 16.945886 6.992681 1.591519 16.002182 4.315481
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 10.291318 17.549136 9.868233 43.20545 28.574266
#> Trackway_02 6.267952 6.896639 2.785510 35.09946 24.813431
#> Trackway_03 2.281460 4.130870 2.497061 20.56924 11.004872
#> Trackway_04 9.461518 16.510590 8.592397 44.33723 30.531294
#> Trackway_07 1.324704 8.337072 3.298160 21.61563 9.905416
#> Trackway_08 NA 7.064439 2.797257 20.50815 9.460504
#> Trackway_09 7.064439 NA 5.838514 25.80141 17.958517
#> Trackway_13 2.797257 5.838514 NA 26.26213 15.709941
#> Trackway_15 20.508150 25.801407 26.262130 NA 14.596277
#> Trackway_16 9.460504 17.958517 15.709941 14.59628 NA
#> Trackway_18 3.101051 3.191202 4.468363 19.24850 10.553790
#> Trackway_18
#> Trackway_01 16.945886
#> Trackway_02 6.992681
#> Trackway_03 1.591519
#> Trackway_04 16.002182
#> Trackway_07 4.315481
#> Trackway_08 3.101051
#> Trackway_09 3.191202
#> Trackway_13 4.468363
#> Trackway_15 19.248501
#> Trackway_16 10.553790
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[37]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 2.285254 10.695970 2.393106 8.511632
#> Trackway_02 2.285254 NA 6.641954 4.545638 6.099461
#> Trackway_03 10.695970 6.641954 NA 12.056866 4.171260
#> Trackway_04 2.393106 4.545638 12.056866 NA 7.336185
#> Trackway_07 8.511632 6.099461 4.171260 7.336185 NA
#> Trackway_08 16.563116 13.067940 7.475875 14.972646 3.576545
#> Trackway_09 8.250007 6.153760 7.472849 7.342912 2.858914
#> Trackway_13 6.796818 5.230396 5.942077 5.748068 1.379105
#> Trackway_15 44.680285 37.532644 22.569107 44.261405 24.120692
#> Trackway_16 34.653585 27.694249 13.838525 33.977868 12.954279
#> Trackway_18 9.884349 5.821765 1.010623 11.012263 3.274622
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 16.563116 8.250007 6.796818 44.68029 34.65358
#> Trackway_02 13.067940 6.153760 5.230396 37.53264 27.69425
#> Trackway_03 7.475875 7.472849 5.942077 22.56911 13.83852
#> Trackway_04 14.972646 7.342912 5.748068 44.26141 33.97787
#> Trackway_07 3.576545 2.858914 1.379105 24.12069 12.95428
#> Trackway_08 NA 6.127687 6.060550 24.12244 11.34524
#> Trackway_09 6.127687 NA 2.361333 31.27136 19.68783
#> Trackway_13 6.060550 2.361333 NA 29.51324 18.36540
#> Trackway_15 24.122437 31.271355 29.513241 NA 14.43481
#> Trackway_16 11.345244 19.687829 18.365395 14.43481 NA
#> Trackway_18 6.518887 6.202352 4.781923 22.63985 13.32461
#> Trackway_18
#> Trackway_01 9.884349
#> Trackway_02 5.821765
#> Trackway_03 1.010623
#> Trackway_04 11.012263
#> Trackway_07 3.274622
#> Trackway_08 6.518887
#> Trackway_09 6.202352
#> Trackway_13 4.781923
#> Trackway_15 22.639850
#> Trackway_16 13.324610
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[38]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 5.452982 11.361411 3.911244 5.632737
#> Trackway_02 5.452982 NA 6.177818 3.621477 6.638355
#> Trackway_03 11.361411 6.177818 NA 11.017174 4.708898
#> Trackway_04 3.911244 3.621477 11.017174 NA 8.745121
#> Trackway_07 5.632737 6.638355 4.708898 8.745121 NA
#> Trackway_08 8.214481 4.438805 2.244253 8.961339 2.622394
#> Trackway_09 8.260762 3.823288 3.160936 7.870655 4.282678
#> Trackway_13 6.945995 2.474013 2.922839 6.401432 4.384779
#> Trackway_15 42.347122 35.977656 21.463736 44.280000 23.725209
#> Trackway_16 32.130374 26.911441 13.413341 34.654068 12.977315
#> Trackway_18 7.577332 5.395089 2.990236 9.129691 2.238202
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 8.214481 8.260762 6.945995 42.34712 32.13037
#> Trackway_02 4.438805 3.823288 2.474013 35.97766 26.91144
#> Trackway_03 2.244253 3.160936 2.922839 21.46374 13.41334
#> Trackway_04 8.961339 7.870655 6.401432 44.28000 34.65407
#> Trackway_07 2.622394 4.282678 4.384779 23.72521 12.97731
#> Trackway_08 NA 1.972450 1.668930 21.90063 12.43845
#> Trackway_09 1.972450 NA 2.177816 26.29875 17.12905
#> Trackway_13 1.668930 2.177816 NA 26.54829 17.45707
#> Trackway_15 21.900626 26.298751 26.548289 NA 13.86799
#> Trackway_16 12.438451 17.129047 17.457073 13.86799 NA
#> Trackway_18 1.010851 2.615195 2.514899 21.76315 11.85393
#> Trackway_18
#> Trackway_01 7.577332
#> Trackway_02 5.395089
#> Trackway_03 2.990236
#> Trackway_04 9.129691
#> Trackway_07 2.238202
#> Trackway_08 1.010851
#> Trackway_09 2.615195
#> Trackway_13 2.514899
#> Trackway_15 21.763155
#> Trackway_16 11.853929
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[39]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 7.738479 16.003510 3.314511 7.7518623
#> Trackway_02 7.738479 NA 8.166149 6.824010 6.1800359
#> Trackway_03 16.003510 8.166149 NA 16.552444 3.9661800
#> Trackway_04 3.314511 6.824010 16.552444 NA 9.0589682
#> Trackway_07 7.751862 6.180036 3.966180 9.058968 NA
#> Trackway_08 9.426055 5.990562 3.177272 10.380722 0.9661758
#> Trackway_09 15.500297 7.009694 2.226751 15.673573 7.1546569
#> Trackway_13 10.857305 3.940179 3.105875 10.750578 3.8919150
#> Trackway_15 42.534222 35.424327 19.627616 44.898024 20.6818154
#> Trackway_16 31.803647 26.582204 12.660585 34.697108 10.9250212
#> Trackway_18 13.801173 6.714443 1.125838 14.411962 2.9245402
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 9.4260553 15.500297 10.857305 42.53422 31.80365
#> Trackway_02 5.9905616 7.009694 3.940179 35.42433 26.58220
#> Trackway_03 3.1772716 2.226751 3.105875 19.62762 12.66058
#> Trackway_04 10.3807224 15.673573 10.750578 44.89802 34.69711
#> Trackway_07 0.9661758 7.154657 3.891915 20.68182 10.92502
#> Trackway_08 NA 6.155722 3.111555 20.52164 11.26050
#> Trackway_09 6.1557222 NA 3.527393 27.08377 20.57704
#> Trackway_13 3.1115553 3.527393 NA 25.50102 17.37932
#> Trackway_15 20.5216440 27.083773 25.501022 NA 13.88959
#> Trackway_16 11.2605043 20.577040 17.379324 13.88959 NA
#> Trackway_18 2.0958998 2.942211 1.858981 20.08873 12.28937
#> Trackway_18
#> Trackway_01 13.801173
#> Trackway_02 6.714443
#> Trackway_03 1.125838
#> Trackway_04 14.411962
#> Trackway_07 2.924540
#> Trackway_08 2.095900
#> Trackway_09 2.942211
#> Trackway_13 1.858981
#> Trackway_15 20.088733
#> Trackway_16 12.289368
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[40]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 11.305138 18.004649 8.179666 6.497259
#> Trackway_02 11.305138 NA 7.123675 3.806970 9.194914
#> Trackway_03 18.004649 7.123675 NA 12.238739 6.178863
#> Trackway_04 8.179666 3.806970 12.238739 NA 9.971185
#> Trackway_07 6.497259 9.194914 6.178863 9.971185 NA
#> Trackway_08 10.143929 6.533946 4.463771 8.356228 1.983896
#> Trackway_09 15.815670 5.459352 2.482416 9.951812 7.443899
#> Trackway_13 13.064782 3.366445 3.445307 7.040130 5.996040
#> Trackway_15 45.159269 37.044918 22.655981 44.268737 23.863081
#> Trackway_16 30.818184 26.384705 13.665430 32.887099 10.920502
#> Trackway_18 12.655115 5.454254 3.378086 9.086847 3.265737
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 10.143929 15.815670 13.064782 45.15927 30.81818
#> Trackway_02 6.533946 5.459352 3.366445 37.04492 26.38471
#> Trackway_03 4.463771 2.482416 3.445307 22.65598 13.66543
#> Trackway_04 8.356228 9.951812 7.040130 44.26874 32.88710
#> Trackway_07 1.983896 7.443899 5.996040 23.86308 10.92050
#> Trackway_08 NA 5.202005 3.623188 22.54881 10.67762
#> Trackway_09 5.202005 NA 2.769234 27.64733 18.22616
#> Trackway_13 3.623188 2.769234 NA 27.39329 17.08980
#> Trackway_15 22.548807 27.647333 27.393287 NA 15.60960
#> Trackway_16 10.677624 18.226164 17.089798 15.60960 NA
#> Trackway_18 1.303233 3.755568 2.501189 21.90084 10.89844
#> Trackway_18
#> Trackway_01 12.655115
#> Trackway_02 5.454254
#> Trackway_03 3.378086
#> Trackway_04 9.086847
#> Trackway_07 3.265737
#> Trackway_08 1.303233
#> Trackway_09 3.755568
#> Trackway_13 2.501189
#> Trackway_15 21.900843
#> Trackway_16 10.898436
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[41]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 6.267979 12.397552 2.437078 9.347222
#> Trackway_02 6.267979 NA 6.360009 6.283511 5.310868
#> Trackway_03 12.397552 6.360009 NA 11.992274 1.753138
#> Trackway_04 2.437078 6.283511 11.992274 NA 8.872873
#> Trackway_07 9.347222 5.310868 1.753138 8.872873 NA
#> Trackway_08 8.441235 5.681832 2.447711 7.699205 1.421569
#> Trackway_09 10.069770 4.699350 1.837258 9.885410 2.781588
#> Trackway_13 7.484482 2.664798 3.003357 7.383316 1.726037
#> Trackway_15 43.607587 37.953161 22.100273 43.968024 23.108158
#> Trackway_16 33.055504 28.391917 13.366133 33.085641 13.507913
#> Trackway_18 16.898111 9.992003 2.152621 16.703007 3.866444
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 8.441235 10.069770 7.484482 43.60759 33.05550
#> Trackway_02 5.681832 4.699350 2.664798 37.95316 28.39192
#> Trackway_03 2.447711 1.837258 3.003357 22.10027 13.36613
#> Trackway_04 7.699205 9.885410 7.383316 43.96802 33.08564
#> Trackway_07 1.421569 2.781588 1.726037 23.10816 13.50791
#> Trackway_08 NA 3.656394 3.060352 22.28751 12.26738
#> Trackway_09 3.656394 NA 2.810358 28.59729 19.69864
#> Trackway_13 3.060352 2.810358 NA 28.44917 18.99547
#> Trackway_15 22.287506 28.597286 28.449171 NA 13.09694
#> Trackway_16 12.267378 19.698640 18.995469 13.09694 NA
#> Trackway_18 4.260129 4.560191 5.783364 20.68691 13.14732
#> Trackway_18
#> Trackway_01 16.898111
#> Trackway_02 9.992003
#> Trackway_03 2.152621
#> Trackway_04 16.703007
#> Trackway_07 3.866444
#> Trackway_08 4.260129
#> Trackway_09 4.560191
#> Trackway_13 5.783364
#> Trackway_15 20.686911
#> Trackway_16 13.147321
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[42]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 20.645982 23.474551 9.334112 13.102966
#> Trackway_02 20.645982 NA 6.071204 14.807687 8.889107
#> Trackway_03 23.474551 6.071204 NA 19.323362 4.701571
#> Trackway_04 9.334112 14.807687 19.323362 NA 9.865220
#> Trackway_07 13.102966 8.889107 4.701571 9.865220 NA
#> Trackway_08 21.948275 6.192199 1.018484 18.461058 3.941482
#> Trackway_09 12.872795 7.802747 7.302083 8.771599 2.038948
#> Trackway_13 15.614928 5.621408 5.252464 9.867094 2.578433
#> Trackway_15 44.193414 35.063004 20.492431 46.661580 22.365388
#> Trackway_16 30.893702 27.674226 13.546814 35.354312 12.171600
#> Trackway_18 16.088948 7.041114 3.167137 12.042678 1.547416
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 21.948275 12.872795 15.614928 44.19341 30.89370
#> Trackway_02 6.192199 7.802747 5.621408 35.06300 27.67423
#> Trackway_03 1.018484 7.302083 5.252464 20.49243 13.54681
#> Trackway_04 18.461058 8.771599 9.867094 46.66158 35.35431
#> Trackway_07 3.941482 2.038948 2.578433 22.36539 12.17160
#> Trackway_08 NA 6.416372 4.688724 20.62799 13.08264
#> Trackway_09 6.416372 NA 2.652743 28.29433 18.17932
#> Trackway_13 4.688724 2.652743 NA 27.26253 17.89711
#> Trackway_15 20.627994 28.294331 27.262534 NA 14.39166
#> Trackway_16 13.082643 18.179316 17.897111 14.39166 NA
#> Trackway_18 2.544599 2.619039 1.803348 21.54863 12.33306
#> Trackway_18
#> Trackway_01 16.088948
#> Trackway_02 7.041114
#> Trackway_03 3.167137
#> Trackway_04 12.042678
#> Trackway_07 1.547416
#> Trackway_08 2.544599
#> Trackway_09 2.619039
#> Trackway_13 1.803348
#> Trackway_15 21.548631
#> Trackway_16 12.333060
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[43]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 8.901559 18.0387888 2.249235 8.987016
#> Trackway_02 8.901559 NA 8.4962310 10.848428 4.673806
#> Trackway_03 18.038789 8.496231 NA 19.830650 4.734151
#> Trackway_04 2.249235 10.848428 19.8306499 NA 10.623270
#> Trackway_07 8.987016 4.673806 4.7341509 10.623270 NA
#> Trackway_08 10.740007 5.347368 3.4014561 12.241340 1.705656
#> Trackway_09 15.834033 6.880320 2.3863484 17.801004 5.236069
#> Trackway_13 11.113977 3.813672 4.2999737 12.955727 2.682496
#> Trackway_15 44.501323 36.794870 20.3288092 45.519387 23.725006
#> Trackway_16 32.492732 26.633643 12.2643333 33.112501 13.179203
#> Trackway_18 16.108750 7.125628 0.9786933 17.838838 3.808984
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 10.740007 15.834033 11.113977 44.50132 32.49273
#> Trackway_02 5.347368 6.880320 3.813672 36.79487 26.63364
#> Trackway_03 3.401456 2.386348 4.299974 20.32881 12.26433
#> Trackway_04 12.241340 17.801004 12.955727 45.51939 33.11250
#> Trackway_07 1.705656 5.236069 2.682496 23.72501 13.17920
#> Trackway_08 NA 4.310224 1.867146 22.05452 11.89251
#> Trackway_09 4.310224 NA 3.578634 25.92361 17.44377
#> Trackway_13 1.867146 3.578634 NA 26.95060 17.16053
#> Trackway_15 22.054523 25.923610 26.950596 NA 13.67751
#> Trackway_16 11.892509 17.443770 17.160530 13.67751 NA
#> Trackway_18 2.574056 2.046224 3.113991 21.07617 12.47721
#> Trackway_18
#> Trackway_01 16.1087504
#> Trackway_02 7.1256276
#> Trackway_03 0.9786933
#> Trackway_04 17.8388377
#> Trackway_07 3.8089838
#> Trackway_08 2.5740556
#> Trackway_09 2.0462240
#> Trackway_13 3.1139905
#> Trackway_15 21.0761687
#> Trackway_16 12.4772142
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[44]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 8.187312 14.759885 6.031440 5.823240
#> Trackway_02 8.187312 NA 8.190403 5.379692 7.827316
#> Trackway_03 14.759885 8.190403 NA 15.149586 4.706158
#> Trackway_04 6.031440 5.379692 15.149586 NA 9.230387
#> Trackway_07 5.823240 7.827316 4.706158 9.230387 NA
#> Trackway_08 10.613460 6.149763 2.556547 11.551914 2.706494
#> Trackway_09 12.627971 6.685662 2.495892 13.265693 6.117311
#> Trackway_13 11.134433 4.566599 2.658402 10.166276 5.256318
#> Trackway_15 42.539842 38.254303 21.784329 47.471865 23.339241
#> Trackway_16 32.277967 29.790250 14.490532 38.133931 13.539124
#> Trackway_18 11.592442 6.562598 1.741395 12.304776 3.210109
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 10.6134604 12.627971 11.134433 42.53984 32.27797
#> Trackway_02 6.1497634 6.685662 4.566599 38.25430 29.79025
#> Trackway_03 2.5565466 2.495892 2.658402 21.78433 14.49053
#> Trackway_04 11.5519139 13.265693 10.166276 47.47186 38.13393
#> Trackway_07 2.7064937 6.117311 5.256318 23.33924 13.53912
#> Trackway_08 NA 2.924848 3.073610 21.43413 12.79614
#> Trackway_09 2.9248478 NA 2.875045 27.58518 20.05868
#> Trackway_13 3.0736100 2.875045 NA 27.65857 19.76178
#> Trackway_15 21.4341257 27.585176 27.658574 NA 12.83801
#> Trackway_16 12.7961404 20.058678 19.761778 12.83801 NA
#> Trackway_18 0.8456905 2.793901 2.343896 21.59536 13.39937
#> Trackway_18
#> Trackway_01 11.5924424
#> Trackway_02 6.5625979
#> Trackway_03 1.7413952
#> Trackway_04 12.3047756
#> Trackway_07 3.2101086
#> Trackway_08 0.8456905
#> Trackway_09 2.7939012
#> Trackway_13 2.3438965
#> Trackway_15 21.5953648
#> Trackway_16 13.3993697
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[45]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 7.012619 10.934448 3.244534 7.134277
#> Trackway_02 7.012619 NA 4.794736 7.852201 4.703296
#> Trackway_03 10.934448 4.794736 NA 12.169738 2.013760
#> Trackway_04 3.244534 7.852201 12.169738 NA 8.217806
#> Trackway_07 7.134277 4.703296 2.013760 8.217806 NA
#> Trackway_08 7.706183 7.462931 3.058620 9.101414 1.767297
#> Trackway_09 11.162780 4.762200 2.258404 13.001876 3.740352
#> Trackway_13 7.821895 2.696881 1.855539 8.445751 2.275285
#> Trackway_15 43.976271 36.471502 22.710055 47.597434 23.701124
#> Trackway_16 32.876216 26.833999 13.390444 36.419344 13.225169
#> Trackway_18 13.455531 6.425756 1.268766 14.988413 3.050215
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 7.706183 11.162780 7.821895 43.97627 32.87622
#> Trackway_02 7.462931 4.762200 2.696881 36.47150 26.83400
#> Trackway_03 3.058620 2.258404 1.855539 22.71006 13.39044
#> Trackway_04 9.101414 13.001876 8.445751 47.59743 36.41934
#> Trackway_07 1.767297 3.740352 2.275285 23.70112 13.22517
#> Trackway_08 NA 5.185760 3.850512 22.69623 11.64394
#> Trackway_09 5.185760 NA 2.584599 27.43111 18.42299
#> Trackway_13 3.850512 2.584599 NA 27.71497 17.91996
#> Trackway_15 22.696231 27.431105 27.714969 NA 14.36290
#> Trackway_16 11.643937 18.422988 17.919963 14.36290 NA
#> Trackway_18 3.704642 2.390783 3.141118 21.72387 12.96114
#> Trackway_18
#> Trackway_01 13.455531
#> Trackway_02 6.425756
#> Trackway_03 1.268766
#> Trackway_04 14.988413
#> Trackway_07 3.050215
#> Trackway_08 3.704642
#> Trackway_09 2.390783
#> Trackway_13 3.141118
#> Trackway_15 21.723868
#> Trackway_16 12.961135
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[46]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 9.935120 13.687312 12.911671 7.787135
#> Trackway_02 9.935120 NA 5.355850 5.119396 9.117818
#> Trackway_03 13.687312 5.355850 NA 8.917070 4.060820
#> Trackway_04 12.911671 5.119396 8.917070 NA 13.880047
#> Trackway_07 7.787135 9.117818 4.060820 13.880047 NA
#> Trackway_08 17.182418 7.780603 1.452629 11.649985 5.174412
#> Trackway_09 16.798846 7.731596 2.913983 10.924421 7.773772
#> Trackway_13 4.201222 7.267827 5.639013 11.879158 2.077132
#> Trackway_15 44.591645 36.701456 21.879024 43.378587 23.484904
#> Trackway_16 31.349850 26.650033 12.289669 35.216806 11.043986
#> Trackway_18 16.196175 7.315871 1.070702 10.601976 4.666935
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 17.1824181 16.798846 4.201222 44.59164 31.34985
#> Trackway_02 7.7806034 7.731596 7.267827 36.70146 26.65003
#> Trackway_03 1.4526292 2.913983 5.639013 21.87902 12.28967
#> Trackway_04 11.6499852 10.924421 11.879158 43.37859 35.21681
#> Trackway_07 5.1744123 7.773772 2.077132 23.48490 11.04399
#> Trackway_08 NA 1.766693 7.422983 20.64082 12.00140
#> Trackway_09 1.7666925 NA 8.144263 25.33919 17.21992
#> Trackway_13 7.4229827 8.144263 NA 28.13579 15.86794
#> Trackway_15 20.6408159 25.339193 28.135789 NA 16.00262
#> Trackway_16 12.0013985 17.219920 15.867939 16.00262 NA
#> Trackway_18 0.7584716 2.081876 6.848948 21.18739 12.14527
#> Trackway_18
#> Trackway_01 16.1961748
#> Trackway_02 7.3158706
#> Trackway_03 1.0707022
#> Trackway_04 10.6019763
#> Trackway_07 4.6669351
#> Trackway_08 0.7584716
#> Trackway_09 2.0818756
#> Trackway_13 6.8489475
#> Trackway_15 21.1873928
#> Trackway_16 12.1452656
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[47]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 2.362129 11.270181 2.550610 8.210519
#> Trackway_02 2.362129 NA 8.264439 1.748210 6.939814
#> Trackway_03 11.270181 8.264439 NA 11.858321 5.323403
#> Trackway_04 2.550610 1.748210 11.858321 NA 9.996871
#> Trackway_07 8.210519 6.939814 5.323403 9.996871 NA
#> Trackway_08 7.985933 5.648183 3.519347 9.042956 2.594859
#> Trackway_09 7.727752 5.737030 3.450680 8.823972 5.426588
#> Trackway_13 4.393537 3.573303 4.893090 5.642678 3.332412
#> Trackway_15 43.241554 37.339547 22.085193 45.300121 23.648599
#> Trackway_16 32.422945 26.971509 13.679722 34.787707 11.968801
#> Trackway_18 8.227609 5.893829 2.227798 9.165235 3.292294
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 7.985933 7.727752 4.393537 43.24155 32.42294
#> Trackway_02 5.648183 5.737030 3.573303 37.33955 26.97151
#> Trackway_03 3.519347 3.450680 4.893090 22.08519 13.67972
#> Trackway_04 9.042956 8.823972 5.642678 45.30012 34.78771
#> Trackway_07 2.594859 5.426588 3.332412 23.64860 11.96880
#> Trackway_08 NA 2.951954 2.147550 21.49552 11.01020
#> Trackway_09 2.951954 NA 3.126244 27.36790 17.75622
#> Trackway_13 2.147550 3.126244 NA 27.47646 16.86525
#> Trackway_15 21.495515 27.367896 27.476458 NA 14.66636
#> Trackway_16 11.010197 17.756221 16.865252 14.66636 NA
#> Trackway_18 1.332135 2.225394 2.259626 21.89774 12.11968
#> Trackway_18
#> Trackway_01 8.227609
#> Trackway_02 5.893829
#> Trackway_03 2.227798
#> Trackway_04 9.165235
#> Trackway_07 3.292294
#> Trackway_08 1.332135
#> Trackway_09 2.225394
#> Trackway_13 2.259626
#> Trackway_15 21.897742
#> Trackway_16 12.119682
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[48]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 6.384667 12.7032975 4.834582 6.666980
#> Trackway_02 6.384667 NA 6.0558450 6.387312 6.759475
#> Trackway_03 12.703297 6.055845 NA 13.699159 4.070116
#> Trackway_04 4.834582 6.387312 13.6991586 NA 9.737441
#> Trackway_07 6.666980 6.759475 4.0701162 9.737441 NA
#> Trackway_08 10.850642 4.840157 1.0354335 11.996791 3.177561
#> Trackway_09 5.666023 3.109558 4.5688603 7.713311 3.678367
#> Trackway_13 7.666108 2.353464 3.1178625 8.102993 3.946158
#> Trackway_15 43.089564 34.801162 20.8112940 46.341075 22.561113
#> Trackway_16 33.182691 26.709991 13.5368905 37.303736 12.596839
#> Trackway_18 13.407844 6.571737 0.3915817 14.406724 4.428750
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 10.850642 5.666023 7.666108 43.08956 33.18269
#> Trackway_02 4.840157 3.109558 2.353464 34.80116 26.70999
#> Trackway_03 1.035433 4.568860 3.117862 20.81129 13.53689
#> Trackway_04 11.996791 7.713311 8.102993 46.34107 37.30374
#> Trackway_07 3.177561 3.678367 3.946158 22.56111 12.59684
#> Trackway_08 NA 3.548264 2.332359 20.96147 13.01063
#> Trackway_09 3.548264 NA 2.730387 28.90707 19.93203
#> Trackway_13 2.332359 2.730387 NA 27.06927 18.89974
#> Trackway_15 20.961466 28.907068 27.069273 NA 14.16961
#> Trackway_16 13.010629 19.932027 18.899736 14.16961 NA
#> Trackway_18 1.347679 4.982666 3.587440 20.55319 13.54003
#> Trackway_18
#> Trackway_01 13.4078442
#> Trackway_02 6.5717371
#> Trackway_03 0.3915817
#> Trackway_04 14.4067243
#> Trackway_07 4.4287498
#> Trackway_08 1.3476791
#> Trackway_09 4.9826664
#> Trackway_13 3.5874399
#> Trackway_15 20.5531880
#> Trackway_16 13.5400254
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[49]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 5.426769 9.1058526 3.446174 8.017785
#> Trackway_02 5.426769 NA 9.2125945 6.672246 4.653231
#> Trackway_03 9.105853 9.212594 NA 10.144678 3.944799
#> Trackway_04 3.446174 6.672246 10.1446785 NA 10.134592
#> Trackway_07 8.017785 4.653231 3.9447991 10.134592 NA
#> Trackway_08 10.918659 6.907519 4.3874044 13.253068 1.889874
#> Trackway_09 11.837309 12.653556 3.6519412 12.870989 8.276471
#> Trackway_13 5.054742 6.081111 2.1926849 5.903320 4.338351
#> Trackway_15 43.040731 39.096524 22.3394272 45.584951 24.074620
#> Trackway_16 33.362996 27.939956 13.4386211 36.453739 12.882839
#> Trackway_18 10.825523 10.768894 0.9907471 11.849867 4.506723
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 10.918659 11.837309 5.054742 43.04073 33.36300
#> Trackway_02 6.907519 12.653556 6.081111 39.09652 27.93996
#> Trackway_03 4.387404 3.651941 2.192685 22.33943 13.43862
#> Trackway_04 13.253068 12.870989 5.903320 45.58495 36.45374
#> Trackway_07 1.889874 8.276471 4.338351 24.07462 12.88284
#> Trackway_08 NA 8.924720 5.412575 22.49275 11.01315
#> Trackway_09 8.924720 NA 5.074200 26.60502 19.29977
#> Trackway_13 5.412575 5.074200 NA 27.57938 18.02831
#> Trackway_15 22.492752 26.605024 27.579382 NA 14.41794
#> Trackway_16 11.013148 19.299772 18.028314 14.41794 NA
#> Trackway_18 4.610404 2.811066 3.110334 21.47478 12.90271
#> Trackway_18
#> Trackway_01 10.8255235
#> Trackway_02 10.7688940
#> Trackway_03 0.9907471
#> Trackway_04 11.8498672
#> Trackway_07 4.5067232
#> Trackway_08 4.6104037
#> Trackway_09 2.8110662
#> Trackway_13 3.1103343
#> Trackway_15 21.4747753
#> Trackway_16 12.9027090
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[50]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 10.163545 15.901069 11.439669 7.898904
#> Trackway_02 10.163545 NA 6.953245 2.926071 5.684613
#> Trackway_03 15.901069 6.953245 NA 10.924452 3.950882
#> Trackway_04 11.439669 2.926071 10.924452 NA 9.353757
#> Trackway_07 7.898904 5.684613 3.950882 9.353757 NA
#> Trackway_08 9.886571 5.953519 3.025210 10.051769 1.770241
#> Trackway_09 7.005824 6.078921 6.080787 9.998029 2.090579
#> Trackway_13 8.239924 4.071640 4.766723 6.988109 1.707574
#> Trackway_15 41.292208 34.867594 20.168088 43.793784 21.964110
#> Trackway_16 30.931105 27.258198 13.541789 36.053750 13.025044
#> Trackway_18 14.248621 6.558272 1.172400 10.485935 3.313554
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 9.886571 7.005824 8.239924 41.29221 30.93111
#> Trackway_02 5.953519 6.078921 4.071640 34.86759 27.25820
#> Trackway_03 3.025210 6.080787 4.766723 20.16809 13.54179
#> Trackway_04 10.051769 9.998029 6.988109 43.79378 36.05375
#> Trackway_07 1.770241 2.090579 1.707574 21.96411 13.02504
#> Trackway_08 NA 2.208221 2.284585 20.25496 11.78666
#> Trackway_09 2.208221 NA 2.963561 26.33526 17.24024
#> Trackway_13 2.284585 2.963561 NA 26.40782 17.84961
#> Trackway_15 20.254956 26.335260 26.407824 NA 12.70418
#> Trackway_16 11.786656 17.240236 17.849614 12.70418 NA
#> Trackway_18 2.095991 5.062827 3.928820 19.70606 12.56098
#> Trackway_18
#> Trackway_01 14.248621
#> Trackway_02 6.558272
#> Trackway_03 1.172400
#> Trackway_04 10.485935
#> Trackway_07 3.313554
#> Trackway_08 2.095991
#> Trackway_09 5.062827
#> Trackway_13 3.928820
#> Trackway_15 19.706055
#> Trackway_16 12.560983
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[51]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 9.069630 12.939235 4.284076 7.0114402
#> Trackway_02 9.069630 NA 5.327738 5.812166 6.2146722
#> Trackway_03 12.939235 5.327738 NA 11.474596 3.1043598
#> Trackway_04 4.284076 5.812166 11.474596 NA 7.1160744
#> Trackway_07 7.011440 6.214672 3.104360 7.116074 NA
#> Trackway_08 8.424698 6.217964 2.643863 8.681119 0.8377312
#> Trackway_09 7.263453 10.304494 8.250136 10.723808 4.3859752
#> Trackway_13 9.204765 2.870590 2.502806 7.334105 3.0152240
#> Trackway_15 43.561206 35.898283 21.737468 44.311323 23.3191340
#> Trackway_16 32.260652 26.880776 13.040586 34.101285 12.6759132
#> Trackway_18 11.718742 5.133413 1.357048 10.812577 2.3579970
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 8.4246980 7.263453 9.204765 43.56121 32.26065
#> Trackway_02 6.2179643 10.304494 2.870590 35.89828 26.88078
#> Trackway_03 2.6438632 8.250136 2.502806 21.73747 13.04059
#> Trackway_04 8.6811192 10.723808 7.334105 44.31132 34.10129
#> Trackway_07 0.8377312 4.385975 3.015224 23.31913 12.67591
#> Trackway_08 NA 4.859678 2.598391 22.51134 12.06593
#> Trackway_09 4.8596784 NA 6.905508 29.52464 17.21897
#> Trackway_13 2.5983907 6.905508 NA 27.13015 17.69442
#> Trackway_15 22.5113406 29.524637 27.130153 NA 14.63499
#> Trackway_16 12.0659318 17.218975 17.694424 14.63499 NA
#> Trackway_18 1.6640644 6.899358 2.062062 21.37576 11.93047
#> Trackway_18
#> Trackway_01 11.718742
#> Trackway_02 5.133413
#> Trackway_03 1.357048
#> Trackway_04 10.812577
#> Trackway_07 2.357997
#> Trackway_08 1.664064
#> Trackway_09 6.899358
#> Trackway_13 2.062062
#> Trackway_15 21.375762
#> Trackway_16 11.930468
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[52]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 10.256886 18.9266986 4.926005 8.996360
#> Trackway_02 10.256886 NA 8.0106202 7.359608 5.891756
#> Trackway_03 18.926699 8.010620 NA 17.130506 4.765990
#> Trackway_04 4.926005 7.359608 17.1305064 NA 8.156183
#> Trackway_07 8.996360 5.891756 4.7659903 8.156183 NA
#> Trackway_08 17.770830 7.359611 1.0503718 16.198371 3.864088
#> Trackway_09 10.603954 3.395497 5.5019323 8.794825 3.396795
#> Trackway_13 12.123305 3.050518 4.3296961 9.583262 3.329450
#> Trackway_15 43.725230 35.661900 20.8507110 45.956244 22.123704
#> Trackway_16 32.495923 26.534902 13.7946426 35.412618 12.287813
#> Trackway_18 17.447972 7.098921 0.7612826 15.811179 4.094645
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 17.7708301 10.603954 12.123305 43.72523 32.49592
#> Trackway_02 7.3596109 3.395497 3.050518 35.66190 26.53490
#> Trackway_03 1.0503718 5.501932 4.329696 20.85071 13.79464
#> Trackway_04 16.1983707 8.794825 9.583262 45.95624 35.41262
#> Trackway_07 3.8640880 3.396795 3.329450 22.12370 12.28781
#> Trackway_08 NA 4.582844 3.557999 20.72253 13.12446
#> Trackway_09 4.5828445 NA 2.246056 27.59041 18.41967
#> Trackway_13 3.5579991 2.246056 NA 26.55249 17.82092
#> Trackway_15 20.7225258 27.590412 26.552492 NA 12.98847
#> Trackway_16 13.1244587 18.419666 17.820915 12.98847 NA
#> Trackway_18 0.8484686 4.752376 3.587878 21.01268 13.52951
#> Trackway_18
#> Trackway_01 17.4479720
#> Trackway_02 7.0989210
#> Trackway_03 0.7612826
#> Trackway_04 15.8111787
#> Trackway_07 4.0946455
#> Trackway_08 0.8484686
#> Trackway_09 4.7523765
#> Trackway_13 3.5878784
#> Trackway_15 21.0126766
#> Trackway_16 13.5295126
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[53]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 19.598751 19.169681 8.924979 10.306410
#> Trackway_02 19.598751 NA 4.554987 14.209255 9.945251
#> Trackway_03 19.169681 4.554987 NA 14.484592 4.428771
#> Trackway_04 8.924979 14.209255 14.484592 NA 6.391423
#> Trackway_07 10.306410 9.945251 4.428771 6.391423 NA
#> Trackway_08 16.917460 6.636745 2.091832 13.251945 3.747853
#> Trackway_09 13.764471 5.963865 4.138656 8.531823 4.014422
#> Trackway_13 15.621605 5.095877 2.730451 9.562862 4.294063
#> Trackway_15 43.440423 34.997447 21.681798 46.106584 24.207293
#> Trackway_16 29.419923 26.733278 12.825208 34.217448 12.849075
#> Trackway_18 15.748805 6.785564 1.812943 11.565547 2.938796
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 16.917460 13.764471 15.621605 43.44042 29.41992
#> Trackway_02 6.636745 5.963865 5.095877 34.99745 26.73328
#> Trackway_03 2.091832 4.138656 2.730451 21.68180 12.82521
#> Trackway_04 13.251945 8.531823 9.562862 46.10658 34.21745
#> Trackway_07 3.747853 4.014422 4.294063 24.20729 12.84908
#> Trackway_08 NA 3.896799 3.321019 20.86739 11.07729
#> Trackway_09 3.896799 NA 2.105061 29.05833 18.71567
#> Trackway_13 3.321019 2.105061 NA 27.70000 17.82942
#> Trackway_15 20.867387 29.058327 27.699995 NA 14.44534
#> Trackway_16 11.077288 18.715670 17.829419 14.44534 NA
#> Trackway_18 1.084441 2.681064 2.015160 21.88757 11.88464
#> Trackway_18
#> Trackway_01 15.748805
#> Trackway_02 6.785564
#> Trackway_03 1.812943
#> Trackway_04 11.565547
#> Trackway_07 2.938796
#> Trackway_08 1.084441
#> Trackway_09 2.681064
#> Trackway_13 2.015160
#> Trackway_15 21.887572
#> Trackway_16 11.884645
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[54]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 5.862326 16.718173 2.608190 7.008343
#> Trackway_02 5.862326 NA 10.345633 7.191197 4.680345
#> Trackway_03 16.718173 10.345633 NA 18.922983 4.518172
#> Trackway_04 2.608190 7.191197 18.922983 NA 8.760388
#> Trackway_07 7.008343 4.680345 4.518172 8.760388 NA
#> Trackway_08 9.114889 5.330552 3.818794 10.949358 1.138628
#> Trackway_09 13.706017 7.591989 2.990183 16.012642 5.229504
#> Trackway_13 14.155390 7.635314 2.397522 16.228537 5.250115
#> Trackway_15 44.280932 37.972765 20.888906 46.646152 23.276911
#> Trackway_16 32.765607 27.914378 13.409706 34.815279 12.871684
#> Trackway_18 11.956970 6.731536 2.302307 13.997005 2.303432
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 9.114889 13.706017 14.155390 44.28093 32.76561
#> Trackway_02 5.330552 7.591989 7.635314 37.97277 27.91438
#> Trackway_03 3.818794 2.990183 2.397522 20.88891 13.40971
#> Trackway_04 10.949358 16.012642 16.228537 46.64615 34.81528
#> Trackway_07 1.138628 5.229504 5.250115 23.27691 12.87168
#> Trackway_08 NA 4.371664 4.507894 22.20182 12.08805
#> Trackway_09 4.371664 NA 2.122269 27.51306 19.48676
#> Trackway_13 4.507894 2.122269 NA 26.69709 18.75564
#> Trackway_15 22.201816 27.513056 26.697090 NA 14.43493
#> Trackway_16 12.088053 19.486757 18.755638 14.43493 NA
#> Trackway_18 1.677006 2.760661 2.490319 22.02237 12.97353
#> Trackway_18
#> Trackway_01 11.956970
#> Trackway_02 6.731536
#> Trackway_03 2.302307
#> Trackway_04 13.997005
#> Trackway_07 2.303432
#> Trackway_08 1.677006
#> Trackway_09 2.760661
#> Trackway_13 2.490319
#> Trackway_15 22.022373
#> Trackway_16 12.973535
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[55]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 9.804806 9.744728 4.145462 12.271220
#> Trackway_02 9.804806 NA 12.755955 6.671516 4.545513
#> Trackway_03 9.744728 12.755955 NA 11.521720 5.884687
#> Trackway_04 4.145462 6.671516 11.521720 NA 10.357279
#> Trackway_07 12.271220 4.545513 5.884687 10.357279 NA
#> Trackway_08 11.607513 5.794328 4.630601 10.691910 1.950288
#> Trackway_09 6.753531 9.467805 2.857824 8.139206 6.605284
#> Trackway_13 5.612326 10.123152 2.411087 7.405119 7.074531
#> Trackway_15 43.316425 39.434005 23.077262 45.116113 24.658164
#> Trackway_16 33.385868 26.572876 13.767765 33.730832 11.686101
#> Trackway_18 12.404105 14.803479 1.762087 14.395645 6.581536
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 11.607513 6.753531 5.612326 43.31642 33.38587
#> Trackway_02 5.794328 9.467805 10.123152 39.43401 26.57288
#> Trackway_03 4.630601 2.857824 2.411087 23.07726 13.76777
#> Trackway_04 10.691910 8.139206 7.405119 45.11611 33.73083
#> Trackway_07 1.950288 6.605284 7.074531 24.65816 11.68610
#> Trackway_08 NA 5.276281 5.836003 23.08041 10.87164
#> Trackway_09 5.276281 NA 2.576789 28.61139 18.36443
#> Trackway_13 5.836003 2.576789 NA 28.20992 18.34922
#> Trackway_15 23.080411 28.611391 28.209920 NA 15.75278
#> Trackway_16 10.871637 18.364432 18.349222 15.75278 NA
#> Trackway_18 4.986922 4.439493 3.907322 21.34386 12.71976
#> Trackway_18
#> Trackway_01 12.404105
#> Trackway_02 14.803479
#> Trackway_03 1.762087
#> Trackway_04 14.395645
#> Trackway_07 6.581536
#> Trackway_08 4.986922
#> Trackway_09 4.439493
#> Trackway_13 3.907322
#> Trackway_15 21.343855
#> Trackway_16 12.719764
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[56]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 4.593385 11.772491 9.941318 8.868450
#> Trackway_02 4.593385 NA 6.945092 13.658568 9.159687
#> Trackway_03 11.772491 6.945092 NA 19.121077 5.570346
#> Trackway_04 9.941318 13.658568 19.121077 NA 7.394953
#> Trackway_07 8.868450 9.159687 5.570346 7.394953 NA
#> Trackway_08 8.090570 5.957885 3.042173 13.406456 2.727388
#> Trackway_09 5.669714 5.773622 6.417419 9.279577 3.258842
#> Trackway_13 4.840770 4.270483 4.609515 11.703261 3.841043
#> Trackway_15 44.960160 37.899823 23.231361 47.388794 25.718808
#> Trackway_16 35.120078 29.035500 14.863722 34.747096 14.019735
#> Trackway_18 8.641862 5.645325 2.108465 14.656816 3.580478
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 8.0905696 5.669714 4.840770 44.96016 35.12008
#> Trackway_02 5.9578848 5.773622 4.270483 37.89982 29.03550
#> Trackway_03 3.0421734 6.417419 4.609515 23.23136 14.86372
#> Trackway_04 13.4064563 9.279577 11.703261 47.38879 34.74710
#> Trackway_07 2.7273882 3.258842 3.841043 25.71881 14.01973
#> Trackway_08 NA 2.765088 1.402058 23.78123 13.43464
#> Trackway_09 2.7650881 NA 2.213647 30.86226 20.06198
#> Trackway_13 1.4020576 2.213647 NA 28.50947 18.35797
#> Trackway_15 23.7812343 30.862258 28.509472 NA 15.26326
#> Trackway_16 13.4346385 20.061981 18.357969 15.26326 NA
#> Trackway_18 0.9886808 3.527986 2.178496 23.55335 13.81566
#> Trackway_18
#> Trackway_01 8.6418617
#> Trackway_02 5.6453252
#> Trackway_03 2.1084646
#> Trackway_04 14.6568161
#> Trackway_07 3.5804776
#> Trackway_08 0.9886808
#> Trackway_09 3.5279861
#> Trackway_13 2.1784958
#> Trackway_15 23.5533532
#> Trackway_16 13.8156637
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[57]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 6.681210 15.7145490 14.166880 7.229349
#> Trackway_02 6.681210 NA 8.1798549 8.347735 5.353893
#> Trackway_03 15.714549 8.179855 NA 10.724330 4.373687
#> Trackway_04 14.166880 8.347735 10.7243297 NA 14.470265
#> Trackway_07 7.229349 5.353893 4.3736867 14.470265 NA
#> Trackway_08 15.588775 7.962085 0.9396822 10.835011 3.927015
#> Trackway_09 11.173283 4.813167 3.4320325 9.728303 4.171281
#> Trackway_13 7.070845 3.081140 4.7091929 10.483668 2.554117
#> Trackway_15 44.343130 36.499733 20.9694514 46.150052 23.246373
#> Trackway_16 33.419807 26.965105 13.1526731 38.523194 12.853998
#> Trackway_18 13.881484 6.814678 0.8035571 10.493849 3.623150
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 15.5887748 11.173283 7.070845 44.34313 33.41981
#> Trackway_02 7.9620852 4.813167 3.081140 36.49973 26.96510
#> Trackway_03 0.9396822 3.432033 4.709193 20.96945 13.15267
#> Trackway_04 10.8350106 9.728303 10.483668 46.15005 38.52319
#> Trackway_07 3.9270155 4.171281 2.554117 23.24637 12.85400
#> Trackway_08 NA 3.286516 4.590156 21.06772 12.91792
#> Trackway_09 3.2865164 NA 3.313299 27.41304 18.49996
#> Trackway_13 4.5901556 3.313299 NA 27.57293 17.74579
#> Trackway_15 21.0677223 27.413041 27.572934 NA 13.78395
#> Trackway_16 12.9179181 18.499958 17.745790 13.78395 NA
#> Trackway_18 1.2038585 2.514458 3.628063 21.16053 12.82611
#> Trackway_18
#> Trackway_01 13.8814843
#> Trackway_02 6.8146782
#> Trackway_03 0.8035571
#> Trackway_04 10.4938489
#> Trackway_07 3.6231497
#> Trackway_08 1.2038585
#> Trackway_09 2.5144581
#> Trackway_13 3.6280629
#> Trackway_15 21.1605315
#> Trackway_16 12.8261086
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[58]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 17.204074 25.214466 18.481438 12.656775
#> Trackway_02 17.20407 NA 9.039645 2.082303 6.257575
#> Trackway_03 25.21447 9.039645 NA 12.692227 6.100484
#> Trackway_04 18.48144 2.082303 12.692227 NA 9.433348
#> Trackway_07 12.65678 6.257575 6.100484 9.433348 NA
#> Trackway_08 14.63325 6.200014 5.092454 9.630591 1.747241
#> Trackway_09 19.45196 3.868087 4.617691 6.925087 5.174816
#> Trackway_13 20.50097 4.311207 3.575369 6.914814 5.028145
#> Trackway_15 42.88259 35.274084 20.230344 43.199536 22.878427
#> Trackway_16 30.10619 26.791694 14.162750 34.894310 13.215010
#> Trackway_18 23.40280 8.385285 1.855747 12.547203 5.351725
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 14.633248 19.451960 20.500971 42.88259 30.10619
#> Trackway_02 6.200014 3.868087 4.311207 35.27408 26.79169
#> Trackway_03 5.092454 4.617691 3.575369 20.23034 14.16275
#> Trackway_04 9.630591 6.925087 6.914814 43.19954 34.89431
#> Trackway_07 1.747241 5.174816 5.028145 22.87843 13.21501
#> Trackway_08 NA 4.420531 4.302437 21.16881 11.90371
#> Trackway_09 4.420531 NA 1.629195 26.97997 19.10159
#> Trackway_13 4.302437 1.629195 NA 24.93401 17.31918
#> Trackway_15 21.168805 26.979975 24.934006 NA 12.99244
#> Trackway_16 11.903708 19.101586 17.319177 12.99244 NA
#> Trackway_18 3.977323 3.713584 2.683645 19.14760 12.38538
#> Trackway_18
#> Trackway_01 23.402795
#> Trackway_02 8.385285
#> Trackway_03 1.855747
#> Trackway_04 12.547203
#> Trackway_07 5.351725
#> Trackway_08 3.977323
#> Trackway_09 3.713584
#> Trackway_13 2.683645
#> Trackway_15 19.147598
#> Trackway_16 12.385377
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[59]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 16.380215 25.211714 26.363487 14.6627663
#> Trackway_02 16.38021 NA 11.181546 9.821283 4.9098686
#> Trackway_03 25.21171 11.181546 NA 10.388914 5.3271518
#> Trackway_04 26.36349 9.821283 10.388914 NA 13.8684659
#> Trackway_07 14.66277 4.909869 5.327152 13.868466 NA
#> Trackway_08 15.22590 5.542413 4.820057 14.087658 0.8777534
#> Trackway_09 19.54594 4.263048 5.792189 6.463650 4.7211139
#> Trackway_13 22.26016 7.256002 2.834611 6.045137 5.4793045
#> Trackway_15 42.43981 36.559767 19.717674 42.623378 22.6793325
#> Trackway_16 24.69012 25.449258 12.150289 34.681504 11.2376865
#> Trackway_18 23.18269 9.087461 1.111021 9.301929 4.2190266
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 15.2259011 19.545944 22.260162 42.43981 24.69012
#> Trackway_02 5.5424127 4.263048 7.256002 36.55977 25.44926
#> Trackway_03 4.8200574 5.792189 2.834611 19.71767 12.15029
#> Trackway_04 14.0876577 6.463650 6.045137 42.62338 34.68150
#> Trackway_07 0.8777534 4.721114 5.479304 22.67933 11.23769
#> Trackway_08 NA 4.740600 5.114932 21.80773 10.53492
#> Trackway_09 4.7406000 NA 3.123680 28.88014 19.13258
#> Trackway_13 5.1149324 3.123680 NA 25.29168 16.64755
#> Trackway_15 21.8077318 28.880138 25.291676 NA 15.16696
#> Trackway_16 10.5349182 19.132581 16.647553 15.16696 NA
#> Trackway_18 3.7278774 4.352269 1.582437 20.24309 11.75738
#> Trackway_18
#> Trackway_01 23.182691
#> Trackway_02 9.087461
#> Trackway_03 1.111021
#> Trackway_04 9.301929
#> Trackway_07 4.219027
#> Trackway_08 3.727877
#> Trackway_09 4.352269
#> Trackway_13 1.582437
#> Trackway_15 20.243086
#> Trackway_16 11.757383
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[60]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 9.104833 15.613818 4.112810 6.274459
#> Trackway_02 9.104833 NA 7.573121 7.060947 6.584659
#> Trackway_03 15.613818 7.573121 NA 15.073607 4.647328
#> Trackway_04 4.112810 7.060947 15.073607 NA 6.761783
#> Trackway_07 6.274459 6.584659 4.647328 6.761783 NA
#> Trackway_08 11.449425 5.475840 2.417105 11.175550 3.250273
#> Trackway_09 6.893922 4.533649 5.699421 6.991667 3.060962
#> Trackway_13 8.512549 4.084958 4.062396 7.553778 3.128906
#> Trackway_15 42.794582 37.021133 21.662257 45.260379 24.089774
#> Trackway_16 31.192444 27.439649 13.318426 34.203392 13.224641
#> Trackway_18 10.966047 5.836699 2.266480 10.626771 2.920057
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 11.4494245 6.893922 8.512549 42.79458 31.19244
#> Trackway_02 5.4758403 4.533649 4.084958 37.02113 27.43965
#> Trackway_03 2.4171048 5.699421 4.062396 21.66226 13.31843
#> Trackway_04 11.1755497 6.991667 7.553778 45.26038 34.20339
#> Trackway_07 3.2502735 3.060962 3.128906 24.08977 13.22464
#> Trackway_08 NA 2.858107 2.260040 21.27460 11.61104
#> Trackway_09 2.8581065 NA 2.142560 29.10758 18.66376
#> Trackway_13 2.2600400 2.142560 NA 27.35468 17.36403
#> Trackway_15 21.2746030 29.107584 27.354681 NA 13.80028
#> Trackway_16 11.6110439 18.663760 17.364029 13.80028 NA
#> Trackway_18 0.7579561 2.642898 1.744767 21.69381 12.05296
#> Trackway_18
#> Trackway_01 10.9660470
#> Trackway_02 5.8366991
#> Trackway_03 2.2664797
#> Trackway_04 10.6267707
#> Trackway_07 2.9200567
#> Trackway_08 0.7579561
#> Trackway_09 2.6428980
#> Trackway_13 1.7447675
#> Trackway_15 21.6938066
#> Trackway_16 12.0529556
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[61]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 8.943173 15.414807 2.605009 7.549653
#> Trackway_02 8.943173 NA 6.329391 8.504048 6.612758
#> Trackway_03 15.414807 6.329391 NA 14.972326 4.082780
#> Trackway_04 2.605009 8.504048 14.972326 NA 7.064740
#> Trackway_07 7.549653 6.612758 4.082780 7.064740 NA
#> Trackway_08 14.120843 5.427960 1.264638 13.562497 3.735271
#> Trackway_09 15.367722 5.619546 2.313274 14.971856 7.315094
#> Trackway_13 9.245681 2.882916 3.474632 8.772261 3.425467
#> Trackway_15 44.942926 36.991579 21.735943 45.506553 23.718520
#> Trackway_16 33.988859 27.720163 13.546635 34.304032 13.232153
#> Trackway_18 14.269611 5.678511 1.029620 13.827462 3.580981
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 14.1208430 15.367722 9.245681 44.94293 33.98886
#> Trackway_02 5.4279601 5.619546 2.882916 36.99158 27.72016
#> Trackway_03 1.2646383 2.313274 3.474632 21.73594 13.54664
#> Trackway_04 13.5624974 14.971856 8.772261 45.50655 34.30403
#> Trackway_07 3.7352708 7.315094 3.425467 23.71852 13.23215
#> Trackway_08 NA 3.183049 2.833770 21.04894 12.46760
#> Trackway_09 3.1830494 NA 4.605454 28.51762 20.81323
#> Trackway_13 2.8337700 4.605454 NA 27.22339 17.77851
#> Trackway_15 21.0489424 28.517616 27.223387 NA 13.79106
#> Trackway_16 12.4675956 20.813228 17.778510 13.79106 NA
#> Trackway_18 0.3940386 3.372356 2.768911 21.29470 12.66824
#> Trackway_18
#> Trackway_01 14.2696109
#> Trackway_02 5.6785112
#> Trackway_03 1.0296198
#> Trackway_04 13.8274619
#> Trackway_07 3.5809815
#> Trackway_08 0.3940386
#> Trackway_09 3.3723557
#> Trackway_13 2.7689113
#> Trackway_15 21.2946975
#> Trackway_16 12.6682431
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[62]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 13.501762 19.750972 20.220902 13.668550
#> Trackway_02 13.50176 NA 6.976809 6.914808 4.054504
#> Trackway_03 19.75097 6.976809 NA 9.381554 2.951871
#> Trackway_04 20.22090 6.914808 9.381554 NA 10.741227
#> Trackway_07 13.66855 4.054504 2.951871 10.741227 NA
#> Trackway_08 12.92878 5.865411 3.731355 13.225430 2.270409
#> Trackway_09 22.21667 8.708145 2.973800 9.612866 6.550787
#> Trackway_13 20.10094 6.830534 1.914528 6.759043 4.620385
#> Trackway_15 44.04046 35.699619 21.211037 43.907698 22.706936
#> Trackway_16 32.47305 27.134296 14.090380 37.271148 13.827840
#> Trackway_18 16.35023 5.423812 1.959607 10.206046 1.743573
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 12.928785 22.216671 20.100942 44.04046 32.47305
#> Trackway_02 5.865411 8.708145 6.830534 35.69962 27.13430
#> Trackway_03 3.731355 2.973800 1.914528 21.21104 14.09038
#> Trackway_04 13.225430 9.612866 6.759043 43.90770 37.27115
#> Trackway_07 2.270409 6.550787 4.620385 22.70694 13.82784
#> Trackway_08 NA 7.386664 5.261995 20.85913 11.55897
#> Trackway_09 7.386664 NA 2.193404 25.82056 19.92796
#> Trackway_13 5.261995 2.193404 NA 24.80964 18.11106
#> Trackway_15 20.859130 25.820562 24.809645 NA 13.42111
#> Trackway_16 11.558972 19.927963 18.111057 13.42111 NA
#> Trackway_18 1.797895 5.102908 3.092200 21.04153 12.75918
#> Trackway_18
#> Trackway_01 16.350229
#> Trackway_02 5.423812
#> Trackway_03 1.959607
#> Trackway_04 10.206046
#> Trackway_07 1.743573
#> Trackway_08 1.797895
#> Trackway_09 5.102908
#> Trackway_13 3.092200
#> Trackway_15 21.041533
#> Trackway_16 12.759175
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[63]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 9.551186 18.704119 10.977082 7.716709
#> Trackway_02 9.551186 NA 9.495282 2.347412 4.748253
#> Trackway_03 18.704119 9.495282 NA 13.224133 5.453533
#> Trackway_04 10.977082 2.347412 13.224133 NA 7.608569
#> Trackway_07 7.716709 4.748253 5.453533 7.608569 NA
#> Trackway_08 7.066831 8.325945 6.143126 12.596099 2.476846
#> Trackway_09 19.430945 10.132121 2.472282 14.105913 9.000195
#> Trackway_13 12.848496 4.099822 4.232506 5.954405 4.148907
#> Trackway_15 43.042304 37.381078 21.681726 45.843801 24.785726
#> Trackway_16 28.175224 25.628079 12.667271 34.133181 12.395341
#> Trackway_18 13.478038 5.639453 2.754429 8.658663 3.160737
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 7.066831 19.430945 12.848496 43.04230 28.17522
#> Trackway_02 8.325945 10.132121 4.099822 37.38108 25.62808
#> Trackway_03 6.143126 2.472282 4.232506 21.68173 12.66727
#> Trackway_04 12.596099 14.105913 5.954405 45.84380 34.13318
#> Trackway_07 2.476846 9.000195 4.148907 24.78573 12.39534
#> Trackway_08 NA 10.417708 5.772323 23.12616 10.05542
#> Trackway_09 10.417708 NA 5.698411 27.26436 19.22302
#> Trackway_13 5.772323 5.698411 NA 27.46382 16.74693
#> Trackway_15 23.126159 27.264359 27.463821 NA 15.45251
#> Trackway_16 10.055419 19.223019 16.746928 15.45251 NA
#> Trackway_18 3.420223 5.482325 1.653834 22.06470 11.10936
#> Trackway_18
#> Trackway_01 13.478038
#> Trackway_02 5.639453
#> Trackway_03 2.754429
#> Trackway_04 8.658663
#> Trackway_07 3.160737
#> Trackway_08 3.420223
#> Trackway_09 5.482325
#> Trackway_13 1.653834
#> Trackway_15 22.064701
#> Trackway_16 11.109357
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[64]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 4.091506 17.203043 9.715476 6.813162
#> Trackway_02 4.091506 NA 11.435043 6.298786 3.714630
#> Trackway_03 17.203043 11.435043 NA 14.489067 5.079269
#> Trackway_04 9.715476 6.298786 14.489067 NA 9.637475
#> Trackway_07 6.813162 3.714630 5.079269 9.637475 NA
#> Trackway_08 10.957528 6.526628 2.930343 10.063710 2.435059
#> Trackway_09 12.397294 7.725530 3.261287 9.791270 4.773330
#> Trackway_13 15.584696 9.962729 2.170371 11.658742 6.152224
#> Trackway_15 42.586676 36.709256 20.405098 46.985957 23.375138
#> Trackway_16 31.806465 26.704788 13.363717 37.784511 13.741826
#> Trackway_18 10.009620 5.933814 3.391549 10.407984 2.181567
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 10.9575283 12.397294 15.584696 42.58668 31.80646
#> Trackway_02 6.5266285 7.725530 9.962729 36.70926 26.70479
#> Trackway_03 2.9303431 3.261287 2.170371 20.40510 13.36372
#> Trackway_04 10.0637103 9.791270 11.658742 46.98596 37.78451
#> Trackway_07 2.4350586 4.773330 6.152224 23.37514 13.74183
#> Trackway_08 NA 2.898845 3.978150 21.27197 12.48676
#> Trackway_09 2.8988450 NA 3.042282 26.72583 18.63322
#> Trackway_13 3.9781500 3.042282 NA 26.07384 18.92697
#> Trackway_15 21.2719703 26.725826 26.073838 NA 12.60043
#> Trackway_16 12.4867567 18.633224 18.926969 12.60043 NA
#> Trackway_18 0.5273952 3.485240 4.673058 21.34505 12.30309
#> Trackway_18
#> Trackway_01 10.0096197
#> Trackway_02 5.9338138
#> Trackway_03 3.3915487
#> Trackway_04 10.4079843
#> Trackway_07 2.1815668
#> Trackway_08 0.5273952
#> Trackway_09 3.4852403
#> Trackway_13 4.6730584
#> Trackway_15 21.3450492
#> Trackway_16 12.3030931
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[65]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 8.187166 10.408711 3.079009 6.872111
#> Trackway_02 8.187166 NA 5.028099 8.097960 8.627450
#> Trackway_03 10.408711 5.028099 NA 11.046538 3.587660
#> Trackway_04 3.079009 8.097960 11.046538 NA 8.480207
#> Trackway_07 6.872111 8.627450 3.587660 8.480207 NA
#> Trackway_08 8.661854 7.874921 2.970615 9.866620 1.985760
#> Trackway_09 8.129574 3.218054 2.181981 8.711691 5.463250
#> Trackway_13 6.181292 4.882807 3.167018 6.005998 3.183785
#> Trackway_15 43.708061 35.994771 22.652314 45.930592 24.027275
#> Trackway_16 34.280030 28.270039 14.178725 36.345876 13.851675
#> Trackway_18 13.819698 6.482692 1.675672 14.443458 4.922769
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 8.661854 8.129574 6.181292 43.70806 34.28003
#> Trackway_02 7.874921 3.218054 4.882807 35.99477 28.27004
#> Trackway_03 2.970615 2.181981 3.167018 22.65231 14.17872
#> Trackway_04 9.866620 8.711691 6.005998 45.93059 36.34588
#> Trackway_07 1.985760 5.463250 3.183785 24.02727 13.85168
#> Trackway_08 NA 4.544817 2.154316 22.07491 12.20230
#> Trackway_09 4.544817 NA 2.672608 28.78492 20.33299
#> Trackway_13 2.154316 2.672608 NA 26.59790 17.37264
#> Trackway_15 22.074914 28.784920 26.597896 NA 12.91815
#> Trackway_16 12.202301 20.332992 17.372640 12.91815 NA
#> Trackway_18 3.852065 4.092177 4.665406 21.35882 13.61420
#> Trackway_18
#> Trackway_01 13.819698
#> Trackway_02 6.482692
#> Trackway_03 1.675672
#> Trackway_04 14.443458
#> Trackway_07 4.922769
#> Trackway_08 3.852065
#> Trackway_09 4.092177
#> Trackway_13 4.665406
#> Trackway_15 21.358822
#> Trackway_16 13.614201
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[66]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 12.682104 19.2330492 11.632913 9.079533
#> Trackway_02 12.682104 NA 7.7216161 5.771691 5.880820
#> Trackway_03 19.233049 7.721616 NA 15.318362 4.956709
#> Trackway_04 11.632913 5.771691 15.3183617 NA 8.483630
#> Trackway_07 9.079533 5.880820 4.9567088 8.483630 NA
#> Trackway_08 11.508037 5.512161 3.5532941 9.598679 2.033968
#> Trackway_09 12.221845 2.723397 4.8879037 8.649812 3.851293
#> Trackway_13 13.240349 3.106128 4.0850065 7.822407 3.352076
#> Trackway_15 43.219403 35.363251 20.8511607 46.560321 23.914166
#> Trackway_16 31.685767 26.931221 13.7211212 37.490937 14.117370
#> Trackway_18 17.281200 6.398419 0.9111588 13.404402 4.128405
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 11.508037 12.221845 13.240349 43.21940 31.68577
#> Trackway_02 5.512161 2.723397 3.106128 35.36325 26.93122
#> Trackway_03 3.553294 4.887904 4.085007 20.85116 13.72112
#> Trackway_04 9.598679 8.649812 7.822407 46.56032 37.49094
#> Trackway_07 2.033968 3.851293 3.352076 23.91417 14.11737
#> Trackway_08 NA 2.896502 2.054572 21.92486 12.59676
#> Trackway_09 2.896502 NA 2.280377 28.50328 19.78757
#> Trackway_13 2.054572 2.280377 NA 26.62396 18.09656
#> Trackway_15 21.924856 28.503284 26.623962 NA 13.30731
#> Trackway_16 12.596762 19.787571 18.096564 13.30731 NA
#> Trackway_18 2.689722 3.686766 2.968172 21.12865 13.43341
#> Trackway_18
#> Trackway_01 17.2812004
#> Trackway_02 6.3984191
#> Trackway_03 0.9111588
#> Trackway_04 13.4044021
#> Trackway_07 4.1284052
#> Trackway_08 2.6897220
#> Trackway_09 3.6867664
#> Trackway_13 2.9681716
#> Trackway_15 21.1286462
#> Trackway_16 13.4334115
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[67]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 7.954321 18.366136 4.630483 8.0975915
#> Trackway_02 7.954321 NA 10.847592 5.238950 6.1057763
#> Trackway_03 18.366136 10.847592 NA 18.283793 5.1169498
#> Trackway_04 4.630483 5.238950 18.283793 NA 8.7319624
#> Trackway_07 8.097592 6.105776 5.116950 8.731962 NA
#> Trackway_08 15.449005 8.649538 1.991938 15.757314 3.2677724
#> Trackway_09 7.392082 2.660695 8.019597 6.151210 2.9601080
#> Trackway_13 14.570497 7.195026 3.007026 14.040839 5.3625794
#> Trackway_15 42.219156 37.925240 21.284803 45.206775 22.4254766
#> Trackway_16 30.414830 27.642579 13.825630 34.059394 11.8461408
#> Trackway_18 8.802990 5.775439 4.678484 9.157845 0.5525963
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 15.449005 7.392082 14.570497 42.21916 30.41483
#> Trackway_02 8.649538 2.660695 7.195026 37.92524 27.64258
#> Trackway_03 1.991938 8.019597 3.007026 21.28480 13.82563
#> Trackway_04 15.757314 6.151210 14.040839 45.20678 34.05939
#> Trackway_07 3.267772 2.960108 5.362579 22.42548 11.84614
#> Trackway_08 NA 5.938812 2.135132 21.12518 12.49323
#> Trackway_09 5.938812 NA 5.465255 30.54995 20.14951
#> Trackway_13 2.135132 5.465255 NA 26.57013 18.25762
#> Trackway_15 21.125178 30.549949 26.570129 NA 13.75309
#> Trackway_16 12.493234 20.149510 18.257618 13.75309 NA
#> Trackway_18 2.889509 2.587102 4.917968 21.97979 11.64195
#> Trackway_18
#> Trackway_01 8.8029898
#> Trackway_02 5.7754394
#> Trackway_03 4.6784838
#> Trackway_04 9.1578454
#> Trackway_07 0.5525963
#> Trackway_08 2.8895088
#> Trackway_09 2.5871016
#> Trackway_13 4.9179684
#> Trackway_15 21.9797860
#> Trackway_16 11.6419540
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[68]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 10.761745 17.150408 16.714338 6.107375
#> Trackway_02 10.761745 NA 7.251693 6.769193 8.612900
#> Trackway_03 17.150408 7.251693 NA 8.112104 5.651386
#> Trackway_04 16.714338 6.769193 8.112104 NA 15.708718
#> Trackway_07 6.107375 8.612900 5.651386 15.708718 NA
#> Trackway_08 13.718524 5.738692 2.323046 9.911007 3.784802
#> Trackway_09 12.103767 4.180536 3.893902 7.073554 5.533370
#> Trackway_13 6.019031 6.189199 6.228790 13.506943 2.455177
#> Trackway_15 44.508984 37.738299 21.751101 42.905398 24.405266
#> Trackway_16 32.481806 28.241890 13.799661 35.378648 13.147461
#> Trackway_18 13.872009 5.526376 2.084473 9.812783 4.228914
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 13.7185242 12.103767 6.019031 44.50898 32.48181
#> Trackway_02 5.7386918 4.180536 6.189199 37.73830 28.24189
#> Trackway_03 2.3230461 3.893902 6.228790 21.75110 13.79966
#> Trackway_04 9.9110070 7.073554 13.506943 42.90540 35.37865
#> Trackway_07 3.7848016 5.533370 2.455177 24.40527 13.14746
#> Trackway_08 NA 2.726522 3.771552 21.69899 12.33265
#> Trackway_09 2.7265224 NA 4.120324 28.63065 19.37539
#> Trackway_13 3.7715520 4.120324 NA 27.55565 16.65867
#> Trackway_15 21.6989926 28.630647 27.555653 NA 14.35238
#> Trackway_16 12.3326471 19.375393 16.658671 14.35238 NA
#> Trackway_18 0.5853741 2.757285 3.998392 21.25839 12.11776
#> Trackway_18
#> Trackway_01 13.8720091
#> Trackway_02 5.5263760
#> Trackway_03 2.0844732
#> Trackway_04 9.8127827
#> Trackway_07 4.2289141
#> Trackway_08 0.5853741
#> Trackway_09 2.7572850
#> Trackway_13 3.9983925
#> Trackway_15 21.2583931
#> Trackway_16 12.1177629
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[69]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 2.513899 15.451043 2.958934 6.701404
#> Trackway_02 2.513899 NA 11.903820 4.322279 4.713241
#> Trackway_03 15.451043 11.903820 NA 15.250582 4.721891
#> Trackway_04 2.958934 4.322279 15.250582 NA 8.352135
#> Trackway_07 6.701404 4.713241 4.721891 8.352135 NA
#> Trackway_08 8.522503 6.091035 5.142143 10.620644 1.630085
#> Trackway_09 5.370509 3.166088 7.212022 7.008817 1.891084
#> Trackway_13 4.128953 3.038084 6.843178 5.047821 1.595546
#> Trackway_15 43.702523 37.376708 20.966413 45.292939 23.000572
#> Trackway_16 34.029305 27.388420 14.165598 36.243774 13.335558
#> Trackway_18 11.441259 8.441725 2.025810 11.734974 2.716033
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 8.522503 5.370509 4.128953 43.70252 34.02931
#> Trackway_02 6.091035 3.166088 3.038084 37.37671 27.38842
#> Trackway_03 5.142143 7.212022 6.843178 20.96641 14.16560
#> Trackway_04 10.620644 7.008817 5.047821 45.29294 36.24377
#> Trackway_07 1.630085 1.891084 1.595546 23.00057 13.33556
#> Trackway_08 NA 3.592880 3.534277 21.80473 11.79889
#> Trackway_09 3.592880 NA 2.053285 29.59946 20.07308
#> Trackway_13 3.534277 2.053285 NA 28.29499 18.81045
#> Trackway_15 21.804732 29.599456 28.294991 NA 13.50771
#> Trackway_16 11.798891 20.073075 18.810450 13.50771 NA
#> Trackway_18 3.181446 4.385392 4.241678 21.54480 13.41792
#> Trackway_18
#> Trackway_01 11.441259
#> Trackway_02 8.441725
#> Trackway_03 2.025810
#> Trackway_04 11.734974
#> Trackway_07 2.716033
#> Trackway_08 3.181446
#> Trackway_09 4.385392
#> Trackway_13 4.241678
#> Trackway_15 21.544798
#> Trackway_16 13.417924
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[70]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 3.554538 10.4131475 5.275719 6.002968
#> Trackway_02 3.554538 NA 9.0377630 2.827663 3.791087
#> Trackway_03 10.413148 9.037763 NA 14.097372 3.989399
#> Trackway_04 5.275719 2.827663 14.0973723 NA 7.729649
#> Trackway_07 6.002968 3.791087 3.9893990 7.729649 NA
#> Trackway_08 10.038821 8.877463 0.7503227 13.954501 3.612062
#> Trackway_09 6.300133 6.085494 2.7384649 10.536265 3.740875
#> Trackway_13 7.015402 7.109419 2.5748868 10.927414 4.378819
#> Trackway_15 42.834671 37.856864 21.1687262 47.005442 24.461978
#> Trackway_16 32.315404 26.456231 12.0877281 35.413387 13.289858
#> Trackway_18 11.633048 10.414624 1.0517279 15.718119 4.325921
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 10.0388210 6.300133 7.015402 42.83467 32.31540
#> Trackway_02 8.8774626 6.085494 7.109419 37.85686 26.45623
#> Trackway_03 0.7503227 2.738465 2.574887 21.16873 12.08773
#> Trackway_04 13.9545012 10.536265 10.927414 47.00544 35.41339
#> Trackway_07 3.6120622 3.740875 4.378819 24.46198 13.28986
#> Trackway_08 NA 2.634702 2.026145 21.59431 12.30227
#> Trackway_09 2.6347023 NA 2.235611 28.69115 18.83262
#> Trackway_13 2.0261453 2.235611 NA 27.44253 18.08600
#> Trackway_15 21.5943096 28.691147 27.442531 NA 15.01615
#> Trackway_16 12.3022658 18.832619 18.086002 15.01615 NA
#> Trackway_18 0.9612716 3.630426 2.641397 21.48791 12.86524
#> Trackway_18
#> Trackway_01 11.6330475
#> Trackway_02 10.4146237
#> Trackway_03 1.0517279
#> Trackway_04 15.7181189
#> Trackway_07 4.3259214
#> Trackway_08 0.9612716
#> Trackway_09 3.6304257
#> Trackway_13 2.6413968
#> Trackway_15 21.4879124
#> Trackway_16 12.8652390
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[71]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 2.430039 11.1828654 6.032753 6.588392
#> Trackway_02 2.430039 NA 8.4495290 7.226246 4.919325
#> Trackway_03 11.182865 8.449529 NA 17.460725 3.722426
#> Trackway_04 6.032753 7.226246 17.4607250 NA 9.882011
#> Trackway_07 6.588392 4.919325 3.7224261 9.882011 NA
#> Trackway_08 9.270272 6.560236 1.5841616 15.111886 2.543235
#> Trackway_09 6.883074 5.440476 2.9445942 13.500693 4.140376
#> Trackway_13 4.963876 3.285339 3.4958115 9.711954 2.959601
#> Trackway_15 41.192987 35.936695 20.3171126 48.042134 22.014771
#> Trackway_16 32.315162 27.209867 13.2001423 38.154091 12.585274
#> Trackway_18 11.511298 8.645685 0.4193219 17.849824 3.724981
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 9.270272 6.883074 4.963876 41.19299 32.31516
#> Trackway_02 6.560236 5.440476 3.285339 35.93669 27.20987
#> Trackway_03 1.584162 2.944594 3.495811 20.31711 13.20014
#> Trackway_04 15.111886 13.500693 9.711954 48.04213 38.15409
#> Trackway_07 2.543235 4.140376 2.959601 22.01477 12.58527
#> Trackway_08 NA 2.351531 2.617120 20.10812 12.04598
#> Trackway_09 2.351531 NA 2.292477 26.53701 18.70573
#> Trackway_13 2.617120 2.292477 NA 26.29175 17.92743
#> Trackway_15 20.108118 26.537012 26.291746 NA 13.35426
#> Trackway_16 12.045984 18.705732 17.927434 13.35426 NA
#> Trackway_18 1.430666 3.140456 3.656226 20.04140 12.92102
#> Trackway_18
#> Trackway_01 11.5112980
#> Trackway_02 8.6456849
#> Trackway_03 0.4193219
#> Trackway_04 17.8498241
#> Trackway_07 3.7249808
#> Trackway_08 1.4306665
#> Trackway_09 3.1404562
#> Trackway_13 3.6562258
#> Trackway_15 20.0414027
#> Trackway_16 12.9210176
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[72]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 6.624583 14.9644961 8.779852 7.326362
#> Trackway_02 6.624583 NA 8.1745558 3.314540 5.372946
#> Trackway_03 14.964496 8.174556 NA 10.849677 3.854357
#> Trackway_04 8.779852 3.314540 10.8496771 NA 10.082165
#> Trackway_07 7.326362 5.372946 3.8543572 10.082165 NA
#> Trackway_08 8.512093 7.106410 3.9207936 12.371018 1.431707
#> Trackway_09 13.119482 5.866830 2.7899690 7.622520 6.152691
#> Trackway_13 9.026781 3.271919 3.7161266 5.538822 3.075191
#> Trackway_15 43.913129 37.083156 21.4378806 45.111940 23.700299
#> Trackway_16 31.471558 26.060142 11.9435445 34.639930 11.898760
#> Trackway_18 12.993698 6.708399 0.9012814 9.619128 3.172526
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 8.512093 13.119482 9.026781 43.91313 31.47156
#> Trackway_02 7.106410 5.866830 3.271919 37.08316 26.06014
#> Trackway_03 3.920794 2.789969 3.716127 21.43788 11.94354
#> Trackway_04 12.371018 7.622520 5.538822 45.11194 34.63993
#> Trackway_07 1.431707 6.152691 3.075191 23.70030 11.89876
#> Trackway_08 NA 6.803979 4.292755 22.53355 10.50712
#> Trackway_09 6.803979 NA 3.706241 28.98676 19.63571
#> Trackway_13 4.292755 3.706241 NA 28.21718 17.49118
#> Trackway_15 22.533553 28.986755 28.217182 NA 14.87559
#> Trackway_16 10.507116 19.635713 17.491185 14.87559 NA
#> Trackway_18 3.188452 3.300722 2.948559 21.60083 11.60403
#> Trackway_18
#> Trackway_01 12.9936980
#> Trackway_02 6.7083994
#> Trackway_03 0.9012814
#> Trackway_04 9.6191284
#> Trackway_07 3.1725261
#> Trackway_08 3.1884515
#> Trackway_09 3.3007220
#> Trackway_13 2.9485587
#> Trackway_15 21.6008308
#> Trackway_16 11.6040346
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[73]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 2.915032 10.916576 3.435148 9.938924
#> Trackway_02 2.915032 NA 9.520205 4.476663 6.304558
#> Trackway_03 10.916576 9.520205 NA 12.536774 6.574506
#> Trackway_04 3.435148 4.476663 12.536774 NA 11.720850
#> Trackway_07 9.938924 6.304558 6.574506 11.720850 NA
#> Trackway_08 8.333402 5.917413 2.975044 9.608380 4.195579
#> Trackway_09 6.460828 4.048780 5.703333 8.252218 4.187872
#> Trackway_13 4.177668 3.270051 5.137198 5.444951 4.434371
#> Trackway_15 43.203104 37.427165 22.194844 46.327670 25.317043
#> Trackway_16 33.389398 26.757744 14.221569 36.678798 13.264478
#> Trackway_18 8.610461 6.899162 1.960506 10.252661 4.727652
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 8.333402 6.460828 4.177668 43.20310 33.38940
#> Trackway_02 5.917413 4.048780 3.270051 37.42717 26.75774
#> Trackway_03 2.975044 5.703333 5.137198 22.19484 14.22157
#> Trackway_04 9.608380 8.252218 5.444951 46.32767 36.67880
#> Trackway_07 4.195579 4.187872 4.434371 25.31704 13.26448
#> Trackway_08 NA 2.547652 2.296909 22.04919 12.11355
#> Trackway_09 2.547652 NA 2.523901 28.18286 17.62011
#> Trackway_13 2.296909 2.523901 NA 27.94289 17.67714
#> Trackway_15 22.049194 28.182864 27.942885 NA 15.26029
#> Trackway_16 12.113552 17.620110 17.677143 15.26029 NA
#> Trackway_18 1.257460 3.420399 2.963259 22.44708 13.11404
#> Trackway_18
#> Trackway_01 8.610461
#> Trackway_02 6.899162
#> Trackway_03 1.960506
#> Trackway_04 10.252661
#> Trackway_07 4.727652
#> Trackway_08 1.257460
#> Trackway_09 3.420399
#> Trackway_13 2.963259
#> Trackway_15 22.447080
#> Trackway_16 13.114045
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[74]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 5.965762 10.151559 7.558941 10.030226
#> Trackway_02 5.965762 NA 4.550356 12.880615 10.525305
#> Trackway_03 10.151559 4.550356 NA 15.603810 5.368987
#> Trackway_04 7.558941 12.880615 15.603810 NA 8.129125
#> Trackway_07 10.030226 10.525305 5.368987 8.129125 NA
#> Trackway_08 11.050171 5.502299 2.280509 15.751185 4.850794
#> Trackway_09 5.839983 3.008532 3.292740 11.301313 6.403831
#> Trackway_13 4.303158 5.676870 4.622036 7.891306 3.870107
#> Trackway_15 44.475645 36.071026 22.698854 47.396961 24.559546
#> Trackway_16 35.521544 28.347288 14.857874 36.653281 13.943915
#> Trackway_18 11.559803 5.605435 1.083244 16.682289 5.445674
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 11.050171 5.839983 4.303158 44.47564 35.52154
#> Trackway_02 5.502299 3.008532 5.676870 36.07103 28.34729
#> Trackway_03 2.280509 3.292740 4.622036 22.69885 14.85787
#> Trackway_04 15.751185 11.301313 7.891306 47.39696 36.65328
#> Trackway_07 4.850794 6.403831 3.870107 24.55955 13.94392
#> Trackway_08 NA 2.984058 4.707929 21.03054 12.62208
#> Trackway_09 2.984058 NA 3.203640 29.52482 20.94172
#> Trackway_13 4.707929 3.203640 NA 28.68688 19.23718
#> Trackway_15 21.030540 29.524822 28.686883 NA 13.36394
#> Trackway_16 12.622076 20.941725 19.237175 13.36394 NA
#> Trackway_18 1.372993 3.630520 5.030879 21.69809 13.87673
#> Trackway_18
#> Trackway_01 11.559803
#> Trackway_02 5.605435
#> Trackway_03 1.083244
#> Trackway_04 16.682289
#> Trackway_07 5.445674
#> Trackway_08 1.372993
#> Trackway_09 3.630520
#> Trackway_13 5.030879
#> Trackway_15 21.698088
#> Trackway_16 13.876729
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[75]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 10.187546 14.215861 7.399268 6.423305
#> Trackway_02 10.187546 NA 5.540136 6.569512 6.681115
#> Trackway_03 14.215861 5.540136 NA 13.121778 4.038179
#> Trackway_04 7.399268 6.569512 13.121778 NA 7.761280
#> Trackway_07 6.423305 6.681115 4.038179 7.761280 NA
#> Trackway_08 10.480575 6.108840 2.808946 11.024512 2.526390
#> Trackway_09 8.404706 3.819530 3.843927 8.791988 3.224765
#> Trackway_13 7.742267 4.368087 3.887883 7.107839 2.791061
#> Trackway_15 42.944562 35.605494 21.732402 45.881422 23.821121
#> Trackway_16 30.515096 26.242266 12.953720 35.574182 12.548372
#> Trackway_18 10.948477 6.101300 2.536836 11.479380 2.668852
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 10.4805749 8.404706 7.742267 42.94456 30.51510
#> Trackway_02 6.1088395 3.819530 4.368087 35.60549 26.24227
#> Trackway_03 2.8089463 3.843927 3.887883 21.73240 12.95372
#> Trackway_04 11.0245121 8.791988 7.107839 45.88142 35.57418
#> Trackway_07 2.5263899 3.224765 2.791061 23.82112 12.54837
#> Trackway_08 NA 2.823042 2.580682 21.35468 10.85434
#> Trackway_09 2.8230415 NA 1.979372 28.35984 18.07687
#> Trackway_13 2.5806817 1.979372 NA 27.27080 16.76767
#> Trackway_15 21.3546754 28.359838 27.270805 NA 14.81481
#> Trackway_16 10.8543391 18.076869 16.767674 14.81481 NA
#> Trackway_18 0.4036362 2.893127 2.513885 21.32986 11.00258
#> Trackway_18
#> Trackway_01 10.9484768
#> Trackway_02 6.1012999
#> Trackway_03 2.5368358
#> Trackway_04 11.4793802
#> Trackway_07 2.6688519
#> Trackway_08 0.4036362
#> Trackway_09 2.8931267
#> Trackway_13 2.5138850
#> Trackway_15 21.3298589
#> Trackway_16 11.0025800
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[76]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 5.615612 18.742545 2.898397 7.416927
#> Trackway_02 5.615612 NA 11.097637 7.845974 5.511444
#> Trackway_03 18.742545 11.097637 NA 20.950442 5.857120
#> Trackway_04 2.898397 7.845974 20.950442 NA 8.458173
#> Trackway_07 7.416927 5.511444 5.857120 8.458173 NA
#> Trackway_08 10.081470 5.080259 4.383048 11.500314 1.521898
#> Trackway_09 10.334763 4.123720 5.698333 12.638100 5.133908
#> Trackway_13 17.682346 10.016896 2.635333 19.933639 8.759726
#> Trackway_15 43.007093 35.527915 20.035595 44.309582 21.832940
#> Trackway_16 26.856963 22.135353 11.365861 27.444421 9.054695
#> Trackway_18 10.832445 4.881643 3.782923 12.713515 2.316781
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 10.081470 10.334763 17.682346 43.00709 26.856963
#> Trackway_02 5.080259 4.123720 10.016896 35.52792 22.135353
#> Trackway_03 4.383048 5.698333 2.635333 20.03559 11.365861
#> Trackway_04 11.500314 12.638100 19.933639 44.30958 27.444421
#> Trackway_07 1.521898 5.133908 8.759726 21.83294 9.054695
#> Trackway_08 NA 3.406157 6.810106 21.21509 9.319061
#> Trackway_09 3.406157 NA 5.227218 27.92748 16.577983
#> Trackway_13 6.810106 5.227218 NA 26.34872 17.571292
#> Trackway_15 21.215085 27.927476 26.348717 NA 15.006866
#> Trackway_16 9.319061 16.577983 17.571292 15.00687 NA
#> Trackway_18 1.062109 2.258656 5.542473 21.71700 10.276745
#> Trackway_18
#> Trackway_01 10.832445
#> Trackway_02 4.881643
#> Trackway_03 3.782923
#> Trackway_04 12.713515
#> Trackway_07 2.316781
#> Trackway_08 1.062109
#> Trackway_09 2.258656
#> Trackway_13 5.542473
#> Trackway_15 21.716997
#> Trackway_16 10.276745
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[77]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1.595782 10.256478 5.310794 6.277632
#> Trackway_02 1.595782 NA 7.550301 5.551466 4.074871
#> Trackway_03 10.256478 7.550301 NA 9.659263 3.159116
#> Trackway_04 5.310794 5.551466 9.659263 NA 9.211587
#> Trackway_07 6.277632 4.074871 3.159116 9.211587 NA
#> Trackway_08 9.230152 6.046129 1.766618 9.356593 2.040702
#> Trackway_09 9.107880 7.050596 2.037205 8.893420 5.114294
#> Trackway_13 5.538809 3.512202 3.118084 5.689917 2.485697
#> Trackway_15 42.631004 36.279358 21.506127 45.327363 22.691374
#> Trackway_16 32.499563 26.090993 13.310075 36.327908 12.544375
#> Trackway_18 14.048065 10.659896 1.833230 13.518083 4.650760
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 9.230152 9.107880 5.538809 42.63100 32.49956
#> Trackway_02 6.046129 7.050596 3.512202 36.27936 26.09099
#> Trackway_03 1.766618 2.037205 3.118084 21.50613 13.31008
#> Trackway_04 9.356593 8.893420 5.689917 45.32736 36.32791
#> Trackway_07 2.040702 5.114294 2.485697 22.69137 12.54438
#> Trackway_08 NA 3.325607 1.752481 21.04776 11.90182
#> Trackway_09 3.325607 NA 3.542789 26.79205 18.67516
#> Trackway_13 1.752481 3.542789 NA 26.15915 16.68375
#> Trackway_15 21.047759 26.792049 26.159148 NA 13.93765
#> Trackway_16 11.901820 18.675158 16.683750 13.93765 NA
#> Trackway_18 2.774293 3.638696 4.932273 19.94315 12.74833
#> Trackway_18
#> Trackway_01 14.048065
#> Trackway_02 10.659896
#> Trackway_03 1.833230
#> Trackway_04 13.518083
#> Trackway_07 4.650760
#> Trackway_08 2.774293
#> Trackway_09 3.638696
#> Trackway_13 4.932273
#> Trackway_15 19.943150
#> Trackway_16 12.748330
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[78]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 5.283327 9.4415629 6.484327 6.246448
#> Trackway_02 5.283327 NA 4.9325925 8.743638 7.744739
#> Trackway_03 9.441563 4.932592 NA 12.108938 4.117926
#> Trackway_04 6.484327 8.743638 12.1089384 NA 6.781448
#> Trackway_07 6.246448 7.744739 4.1179260 6.781448 NA
#> Trackway_08 10.643533 11.507207 5.2237428 11.487400 2.521250
#> Trackway_09 5.026186 3.225842 3.1214879 7.489356 4.247086
#> Trackway_13 4.282285 3.686981 3.3939142 7.141588 3.290719
#> Trackway_15 42.463962 36.563214 22.8408489 46.255431 25.277547
#> Trackway_16 32.426660 27.441674 13.6929976 34.692229 13.969103
#> Trackway_18 10.366621 5.659535 0.7490113 12.944767 4.540582
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 10.643533 5.026186 4.282285 42.46396 32.42666
#> Trackway_02 11.507207 3.225842 3.686981 36.56321 27.44167
#> Trackway_03 5.223743 3.121488 3.393914 22.84085 13.69300
#> Trackway_04 11.487400 7.489356 7.141588 46.25543 34.69223
#> Trackway_07 2.521250 4.247086 3.290719 25.27755 13.96910
#> Trackway_08 NA 6.861456 5.810632 23.80766 11.72241
#> Trackway_09 6.861456 NA 2.084151 30.06671 20.13226
#> Trackway_13 5.810632 2.084151 NA 29.09280 18.99343
#> Trackway_15 23.807664 30.066707 29.092801 NA 14.49466
#> Trackway_16 11.722408 20.132260 18.993430 14.49466 NA
#> Trackway_18 5.333036 3.690568 4.042312 22.11138 13.11566
#> Trackway_18
#> Trackway_01 10.3666206
#> Trackway_02 5.6595352
#> Trackway_03 0.7490113
#> Trackway_04 12.9447672
#> Trackway_07 4.5405818
#> Trackway_08 5.3330357
#> Trackway_09 3.6905682
#> Trackway_13 4.0423116
#> Trackway_15 22.1113781
#> Trackway_16 13.1156563
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[79]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 8.958110 12.4686994 3.816619 7.480400
#> Trackway_02 8.958110 NA 5.0725131 7.044157 6.621909
#> Trackway_03 12.468699 5.072513 NA 12.338804 2.938876
#> Trackway_04 3.816619 7.044157 12.3388043 NA 8.157624
#> Trackway_07 7.480400 6.621909 2.9388761 8.157624 NA
#> Trackway_08 8.744877 8.815316 3.7387959 10.030974 1.712035
#> Trackway_09 8.681818 4.246770 3.0267842 8.933980 3.115474
#> Trackway_13 6.256993 4.872831 3.7226350 6.448016 1.988326
#> Trackway_15 42.985478 36.652472 21.7493685 45.437250 22.816925
#> Trackway_16 31.082628 27.187375 12.7420219 34.391077 11.832059
#> Trackway_18 11.756330 5.506102 0.8494434 12.184988 2.484054
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 8.744877 8.681818 6.256993 42.98548 31.08263
#> Trackway_02 8.815316 4.246770 4.872831 36.65247 27.18738
#> Trackway_03 3.738796 3.026784 3.722635 21.74937 12.74202
#> Trackway_04 10.030974 8.933980 6.448016 45.43725 34.39108
#> Trackway_07 1.712035 3.115474 1.988326 22.81693 11.83206
#> Trackway_08 NA 4.425972 3.097696 21.59690 10.19474
#> Trackway_09 4.425972 NA 2.806507 28.17112 18.32285
#> Trackway_13 3.097696 2.806507 NA 27.29793 16.59740
#> Trackway_15 21.596899 28.171115 27.297929 NA 15.03031
#> Trackway_16 10.194735 18.322846 16.597400 15.03031 NA
#> Trackway_18 2.983743 2.566166 3.048690 21.38006 11.98416
#> Trackway_18
#> Trackway_01 11.7563305
#> Trackway_02 5.5061021
#> Trackway_03 0.8494434
#> Trackway_04 12.1849880
#> Trackway_07 2.4840542
#> Trackway_08 2.9837433
#> Trackway_09 2.5661663
#> Trackway_13 3.0486904
#> Trackway_15 21.3800612
#> Trackway_16 11.9841629
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[80]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 8.317201 16.305106 4.624813 6.107759
#> Trackway_02 8.317201 NA 8.704550 6.698865 7.241760
#> Trackway_03 16.305106 8.704550 NA 16.103789 5.384051
#> Trackway_04 4.624813 6.698865 16.103789 NA 8.470047
#> Trackway_07 6.107759 7.241760 5.384051 8.470047 NA
#> Trackway_08 13.562662 7.035775 2.090341 13.252163 3.846109
#> Trackway_09 15.105223 7.819293 2.332408 14.626385 7.749112
#> Trackway_13 8.442223 3.813895 4.783302 8.110597 3.420352
#> Trackway_15 43.239824 38.275320 22.120768 46.241946 24.165757
#> Trackway_16 30.783113 27.886662 13.602175 33.946835 12.356932
#> Trackway_18 9.758498 5.745248 3.392134 9.761253 2.256887
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 13.562662 15.105223 8.442223 43.23982 30.78311
#> Trackway_02 7.035775 7.819293 3.813895 38.27532 27.88666
#> Trackway_03 2.090341 2.332408 4.783302 22.12077 13.60217
#> Trackway_04 13.252163 14.626385 8.110597 46.24195 33.94684
#> Trackway_07 3.846109 7.749112 3.420352 24.16576 12.35693
#> Trackway_08 NA 3.260528 3.338920 21.55835 11.86011
#> Trackway_09 3.260528 NA 5.140961 27.66405 19.11579
#> Trackway_13 3.338920 5.140961 NA 28.28236 17.66117
#> Trackway_15 21.558353 27.664054 28.282360 NA 14.78137
#> Trackway_16 11.860110 19.115786 17.661169 14.78137 NA
#> Trackway_18 1.612168 5.356372 2.037301 22.49277 11.79226
#> Trackway_18
#> Trackway_01 9.758498
#> Trackway_02 5.745248
#> Trackway_03 3.392134
#> Trackway_04 9.761253
#> Trackway_07 2.256887
#> Trackway_08 1.612168
#> Trackway_09 5.356372
#> Trackway_13 2.037301
#> Trackway_15 22.492772
#> Trackway_16 11.792258
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[81]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 16.358228 22.857555 17.205824 9.566257
#> Trackway_02 16.358228 NA 8.760811 3.357290 8.438922
#> Trackway_03 22.857555 8.760811 NA 13.205889 6.448431
#> Trackway_04 17.205824 3.357290 13.205889 NA 11.812562
#> Trackway_07 9.566257 8.438922 6.448431 11.812562 NA
#> Trackway_08 10.211851 9.040396 5.450956 13.037245 2.039428
#> Trackway_09 11.808956 5.095273 8.989470 6.830677 3.784923
#> Trackway_13 14.052731 3.821803 5.791922 6.178134 3.837054
#> Trackway_15 43.763757 36.463298 20.374146 45.133419 24.148011
#> Trackway_16 30.718559 27.786672 13.162677 35.939966 13.089211
#> Trackway_18 21.335833 7.386098 0.850740 11.355000 5.677421
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 10.211851 11.808956 14.052731 43.76376 30.71856
#> Trackway_02 9.040396 5.095273 3.821803 36.46330 27.78667
#> Trackway_03 5.450956 8.989470 5.791922 20.37415 13.16268
#> Trackway_04 13.037245 6.830677 6.178134 45.13342 35.93997
#> Trackway_07 2.039428 3.784923 3.837054 24.14801 13.08921
#> Trackway_08 NA 3.909099 3.413866 22.27202 11.43238
#> Trackway_09 3.909099 NA 2.041482 32.08422 21.65542
#> Trackway_13 3.413866 2.041482 NA 26.79868 17.02020
#> Trackway_15 22.272023 32.084218 26.798675 NA 14.23286
#> Trackway_16 11.432383 21.655416 17.020199 14.23286 NA
#> Trackway_18 4.752599 7.674514 4.699586 20.85848 13.12603
#> Trackway_18
#> Trackway_01 21.335833
#> Trackway_02 7.386098
#> Trackway_03 0.850740
#> Trackway_04 11.355000
#> Trackway_07 5.677421
#> Trackway_08 4.752599
#> Trackway_09 7.674514
#> Trackway_13 4.699586
#> Trackway_15 20.858475
#> Trackway_16 13.126032
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[82]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 7.644005 19.392299 6.303665 7.339246
#> Trackway_02 7.644005 NA 10.944630 2.517631 4.805844
#> Trackway_03 19.392299 10.944630 NA 16.147748 5.567443
#> Trackway_04 6.303665 2.517631 16.147748 NA 6.613550
#> Trackway_07 7.339246 4.805844 5.567443 6.613550 NA
#> Trackway_08 7.777176 7.675965 6.170137 10.077438 1.644244
#> Trackway_09 9.553990 4.400978 6.012659 7.321451 2.453244
#> Trackway_13 15.673813 7.812351 2.985015 12.094516 5.583389
#> Trackway_15 44.435720 37.675848 21.258467 45.016919 24.071649
#> Trackway_16 32.334305 27.374554 14.039995 34.523485 13.169822
#> Trackway_18 14.008425 6.976773 2.681805 11.468634 3.044764
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 7.777176 9.553990 15.673813 44.43572 32.33430
#> Trackway_02 7.675965 4.400978 7.812351 37.67585 27.37455
#> Trackway_03 6.170137 6.012659 2.985015 21.25847 14.04000
#> Trackway_04 10.077438 7.321451 12.094516 45.01692 34.52349
#> Trackway_07 1.644244 2.453244 5.583389 24.07165 13.16982
#> Trackway_08 NA 3.561196 6.765114 23.24011 11.83817
#> Trackway_09 3.561196 NA 4.620620 27.18245 16.91691
#> Trackway_13 6.765114 4.620620 NA 26.38968 18.42189
#> Trackway_15 23.240113 27.182446 26.389679 NA 14.98730
#> Trackway_16 11.838174 16.916909 18.421890 14.98730 NA
#> Trackway_18 3.504525 3.049769 2.106803 21.91209 12.75768
#> Trackway_18
#> Trackway_01 14.008425
#> Trackway_02 6.976773
#> Trackway_03 2.681805
#> Trackway_04 11.468634
#> Trackway_07 3.044764
#> Trackway_08 3.504525
#> Trackway_09 3.049769
#> Trackway_13 2.106803
#> Trackway_15 21.912086
#> Trackway_16 12.757680
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[83]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 4.356044 11.832719 5.883954 7.566657
#> Trackway_02 4.356044 NA 6.577584 9.927020 7.705982
#> Trackway_03 11.832719 6.577584 NA 16.039106 4.951602
#> Trackway_04 5.883954 9.927020 16.039106 NA 6.566151
#> Trackway_07 7.566657 7.705982 4.951602 6.566151 NA
#> Trackway_08 7.922920 6.308753 2.988081 10.297888 2.146922
#> Trackway_09 9.544556 4.959464 2.861043 13.087418 4.915995
#> Trackway_13 6.949581 3.418213 2.934346 11.705546 4.826818
#> Trackway_15 44.025411 36.707765 21.291384 44.734181 24.006241
#> Trackway_16 34.230964 27.707875 13.411234 33.611228 13.397422
#> Trackway_18 11.513937 6.069951 1.545961 15.267250 4.819526
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 7.922920 9.544556 6.949581 44.02541 34.23096
#> Trackway_02 6.308753 4.959464 3.418213 36.70777 27.70787
#> Trackway_03 2.988081 2.861043 2.934346 21.29138 13.41123
#> Trackway_04 10.297888 13.087418 11.705546 44.73418 33.61123
#> Trackway_07 2.146922 4.915995 4.826818 24.00624 13.39742
#> Trackway_08 NA 2.936940 2.793701 22.32617 12.61806
#> Trackway_09 2.936940 NA 2.872404 26.22634 17.51099
#> Trackway_13 2.793701 2.872404 NA 27.25694 18.51138
#> Trackway_15 22.326175 26.226344 27.256937 NA 13.70230
#> Trackway_16 12.618065 17.510991 18.511382 13.70230 NA
#> Trackway_18 2.732079 2.133417 3.505367 20.18189 11.88506
#> Trackway_18
#> Trackway_01 11.513937
#> Trackway_02 6.069951
#> Trackway_03 1.545961
#> Trackway_04 15.267250
#> Trackway_07 4.819526
#> Trackway_08 2.732079
#> Trackway_09 2.133417
#> Trackway_13 3.505367
#> Trackway_15 20.181892
#> Trackway_16 11.885062
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[84]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 3.463011 11.3196565 8.422298 6.466892
#> Trackway_02 3.463011 NA 7.6006948 6.523135 6.220054
#> Trackway_03 11.319656 7.600695 NA 8.568198 4.625076
#> Trackway_04 8.422298 6.523135 8.5681982 NA 13.311255
#> Trackway_07 6.466892 6.220054 4.6250757 13.311255 NA
#> Trackway_08 8.919265 8.028164 4.3355984 15.210914 2.041525
#> Trackway_09 12.023332 8.522600 2.2378344 8.074794 7.040271
#> Trackway_13 11.362104 7.491290 2.4626707 6.418350 6.415751
#> Trackway_15 43.451245 37.896861 22.3481529 43.775286 25.085701
#> Trackway_16 33.539299 28.115884 13.7888092 35.695432 14.134159
#> Trackway_18 9.793255 6.200511 0.9618101 9.157084 3.924422
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 8.919265 12.023332 11.362104 43.45124 33.53930
#> Trackway_02 8.028164 8.522600 7.491290 37.89686 28.11588
#> Trackway_03 4.335598 2.237834 2.462671 22.34815 13.78881
#> Trackway_04 15.210914 8.074794 6.418350 43.77529 35.69543
#> Trackway_07 2.041525 7.040271 6.415751 25.08570 14.13416
#> Trackway_08 NA 6.980554 6.664537 23.18972 12.12281
#> Trackway_09 6.980554 NA 1.629027 26.36111 18.36146
#> Trackway_13 6.664537 1.629027 NA 25.41696 17.46288
#> Trackway_15 23.189721 26.361107 25.416955 NA 14.05202
#> Trackway_16 12.122809 18.361459 17.462880 14.05202 NA
#> Trackway_18 3.472468 2.963118 3.035721 22.34684 13.26899
#> Trackway_18
#> Trackway_01 9.7932548
#> Trackway_02 6.2005107
#> Trackway_03 0.9618101
#> Trackway_04 9.1570845
#> Trackway_07 3.9244216
#> Trackway_08 3.4724685
#> Trackway_09 2.9631182
#> Trackway_13 3.0357207
#> Trackway_15 22.3468362
#> Trackway_16 13.2689877
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[85]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 5.080112 14.367339 2.008235 6.308460
#> Trackway_02 5.080112 NA 8.813453 5.504682 7.251882
#> Trackway_03 14.367339 8.813453 NA 15.844892 5.905403
#> Trackway_04 2.008235 5.504682 15.844892 NA 7.221150
#> Trackway_07 6.308460 7.251882 5.905403 7.221150 NA
#> Trackway_08 8.212923 7.572779 5.400684 9.060742 2.004045
#> Trackway_09 11.334389 5.689011 3.222835 12.440076 8.157933
#> Trackway_13 6.005103 3.477345 5.234080 7.360832 3.614600
#> Trackway_15 41.747314 36.138214 20.855967 43.551148 23.208088
#> Trackway_16 32.403219 27.725741 14.214862 34.228560 13.570928
#> Trackway_18 9.656516 5.536007 2.481361 11.335890 3.566202
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 8.212923 11.334389 6.005103 41.74731 32.40322
#> Trackway_02 7.572779 5.689011 3.477345 36.13821 27.72574
#> Trackway_03 5.400684 3.222835 5.234080 20.85597 14.21486
#> Trackway_04 9.060742 12.440076 7.360832 43.55115 34.22856
#> Trackway_07 2.004045 8.157933 3.614600 23.20809 13.57093
#> Trackway_08 NA 8.029803 3.446654 21.24036 11.70701
#> Trackway_09 8.029803 NA 4.883587 28.57015 21.47336
#> Trackway_13 3.446654 4.883587 NA 26.53290 17.91351
#> Trackway_15 21.240356 28.570145 26.532896 NA 12.19797
#> Trackway_16 11.707014 21.473365 17.913505 12.19797 NA
#> Trackway_18 2.961219 3.918582 2.147626 21.09020 13.06607
#> Trackway_18
#> Trackway_01 9.656516
#> Trackway_02 5.536007
#> Trackway_03 2.481361
#> Trackway_04 11.335890
#> Trackway_07 3.566202
#> Trackway_08 2.961219
#> Trackway_09 3.918582
#> Trackway_13 2.147626
#> Trackway_15 21.090202
#> Trackway_16 13.066068
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[86]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 11.336973 15.317996 8.193406 8.2733740
#> Trackway_02 11.336973 NA 6.185900 4.215182 7.0388843
#> Trackway_03 15.317996 6.185900 NA 11.499612 3.2595433
#> Trackway_04 8.193406 4.215182 11.499612 NA 8.2107350
#> Trackway_07 8.273374 7.038884 3.259543 8.210735 NA
#> Trackway_08 10.300167 6.730792 2.873397 8.900688 1.0374017
#> Trackway_09 16.783148 6.694939 2.790690 12.284338 6.3877797
#> Trackway_13 8.917477 4.239274 3.850566 5.187458 2.0642556
#> Trackway_15 42.975992 36.309141 20.829285 43.780368 22.4499912
#> Trackway_16 32.641229 28.601420 13.536558 35.352666 13.2901497
#> Trackway_18 8.156676 8.501144 3.593362 9.900474 0.8921984
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 10.300167 16.783148 8.917477 42.97599 32.64123
#> Trackway_02 6.730792 6.694939 4.239274 36.30914 28.60142
#> Trackway_03 2.873397 2.790690 3.850566 20.82928 13.53656
#> Trackway_04 8.900688 12.284338 5.187458 43.78037 35.35267
#> Trackway_07 1.037402 6.387780 2.064256 22.44999 13.29015
#> Trackway_08 NA 5.828741 2.278136 21.85871 12.83968
#> Trackway_09 5.828741 NA 5.538036 26.18076 19.91114
#> Trackway_13 2.278136 5.538036 NA 27.23770 18.66187
#> Trackway_15 21.858705 26.180761 27.237705 NA 12.99628
#> Trackway_16 12.839681 19.911138 18.661869 12.99628 NA
#> Trackway_18 1.204440 7.032758 3.006890 22.00111 12.58689
#> Trackway_18
#> Trackway_01 8.1566756
#> Trackway_02 8.5011439
#> Trackway_03 3.5933622
#> Trackway_04 9.9004745
#> Trackway_07 0.8921984
#> Trackway_08 1.2044403
#> Trackway_09 7.0327583
#> Trackway_13 3.0068896
#> Trackway_15 22.0011144
#> Trackway_16 12.5868946
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[87]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 4.889333 7.029004 4.501415 7.186549
#> Trackway_02 4.889333 NA 6.604731 2.173109 4.321609
#> Trackway_03 7.029004 6.604731 NA 9.352770 1.652627
#> Trackway_04 4.501415 2.173109 9.352770 NA 7.293669
#> Trackway_07 7.186549 4.321609 1.652627 7.293669 NA
#> Trackway_08 7.600536 6.184307 0.922468 9.413562 1.589822
#> Trackway_09 7.921336 8.499990 2.769977 11.099551 4.824959
#> Trackway_13 7.197246 8.369278 2.296110 10.807322 4.227120
#> Trackway_15 42.938433 38.381329 22.690810 45.795291 23.724249
#> Trackway_16 33.391076 27.405132 12.844725 34.976678 12.961317
#> Trackway_18 10.933110 11.004494 2.368226 14.212617 4.007385
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 7.600536 7.921336 7.197246 42.93843 33.39108
#> Trackway_02 6.184307 8.499990 8.369278 38.38133 27.40513
#> Trackway_03 0.922468 2.769977 2.296110 22.69081 12.84472
#> Trackway_04 9.413562 11.099551 10.807322 45.79529 34.97668
#> Trackway_07 1.589822 4.824959 4.227120 23.72425 12.96132
#> Trackway_08 NA 3.322424 3.180410 22.21413 12.00900
#> Trackway_09 3.322424 NA 2.190014 27.84413 18.89151
#> Trackway_13 3.180410 2.190014 NA 26.75856 18.00014
#> Trackway_15 22.214130 27.844126 26.758561 NA 14.62899
#> Trackway_16 12.008997 18.891513 18.000144 14.62899 NA
#> Trackway_18 2.900078 2.449024 2.432484 21.53945 13.25826
#> Trackway_18
#> Trackway_01 10.933110
#> Trackway_02 11.004494
#> Trackway_03 2.368226
#> Trackway_04 14.212617
#> Trackway_07 4.007385
#> Trackway_08 2.900078
#> Trackway_09 2.449024
#> Trackway_13 2.432484
#> Trackway_15 21.539450
#> Trackway_16 13.258262
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[88]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 6.339004 13.569842 5.66269 7.089445
#> Trackway_02 6.339004 NA 7.191500 11.03254 5.495632
#> Trackway_03 13.569842 7.191500 NA 18.75604 3.169722
#> Trackway_04 5.662690 11.032535 18.756036 NA 11.483003
#> Trackway_07 7.089445 5.495632 3.169722 11.48300 NA
#> Trackway_08 16.874947 9.897368 1.695184 22.16313 4.330933
#> Trackway_09 15.088756 8.951271 2.122261 20.55902 5.487810
#> Trackway_13 8.551040 3.955301 2.876836 13.44911 2.301857
#> Trackway_15 43.371855 37.426454 21.593543 47.14768 22.656969
#> Trackway_16 32.316973 27.680691 13.377258 35.29352 12.618451
#> Trackway_18 11.576390 5.921772 1.195287 16.51875 2.153468
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 16.874947 15.088756 8.551040 43.37185 32.31697
#> Trackway_02 9.897368 8.951271 3.955301 37.42645 27.68069
#> Trackway_03 1.695184 2.122261 2.876836 21.59354 13.37726
#> Trackway_04 22.163125 20.559023 13.449107 47.14768 35.29352
#> Trackway_07 4.330933 5.487810 2.301857 22.65697 12.61845
#> Trackway_08 NA 2.152982 4.857336 20.03782 12.53898
#> Trackway_09 2.152982 NA 4.352815 25.60318 17.99822
#> Trackway_13 4.857336 4.352815 NA 26.95611 17.59696
#> Trackway_15 20.037816 25.603179 26.956114 NA 13.46328
#> Trackway_16 12.538984 17.998218 17.596958 13.46328 NA
#> Trackway_18 2.206778 2.970575 1.885272 21.41351 12.53845
#> Trackway_18
#> Trackway_01 11.576390
#> Trackway_02 5.921772
#> Trackway_03 1.195287
#> Trackway_04 16.518745
#> Trackway_07 2.153468
#> Trackway_08 2.206778
#> Trackway_09 2.970575
#> Trackway_13 1.885272
#> Trackway_15 21.413507
#> Trackway_16 12.538453
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[89]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 5.825014 10.628106 6.378949 9.0364314
#> Trackway_02 5.825014 NA 10.441344 2.048587 4.9551539
#> Trackway_03 10.628106 10.441344 NA 15.157669 3.8649854
#> Trackway_04 6.378949 2.048587 15.157669 NA 8.3698599
#> Trackway_07 9.036431 4.955154 3.864985 8.369860 NA
#> Trackway_08 10.395722 5.646562 4.353198 8.726663 0.9729867
#> Trackway_09 5.219618 6.500262 3.499991 10.070306 4.6360152
#> Trackway_13 3.676215 5.247705 4.690382 7.898996 4.2020140
#> Trackway_15 41.760277 37.171257 20.352359 44.434080 22.0588782
#> Trackway_16 34.194437 27.967496 13.393396 35.234503 12.7741079
#> Trackway_18 7.937108 7.588990 1.737254 11.829391 2.3882792
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 10.3957218 5.219618 3.676215 41.76028 34.19444
#> Trackway_02 5.6465617 6.500262 5.247705 37.17126 27.96750
#> Trackway_03 4.3531980 3.499991 4.690382 20.35236 13.39340
#> Trackway_04 8.7266632 10.070306 7.898996 44.43408 35.23450
#> Trackway_07 0.9729867 4.636015 4.202014 22.05888 12.77411
#> Trackway_08 NA 5.412588 4.422318 22.74377 13.28325
#> Trackway_09 5.4125878 NA 2.687000 28.00480 20.41875
#> Trackway_13 4.4223182 2.687000 NA 28.17512 20.17057
#> Trackway_15 22.7437673 28.004803 28.175122 NA 13.13733
#> Trackway_16 13.2832486 20.418754 20.170572 13.13733 NA
#> Trackway_18 2.7077590 2.226990 2.879409 21.51843 13.55325
#> Trackway_18
#> Trackway_01 7.937108
#> Trackway_02 7.588990
#> Trackway_03 1.737254
#> Trackway_04 11.829391
#> Trackway_07 2.388279
#> Trackway_08 2.707759
#> Trackway_09 2.226990
#> Trackway_13 2.879409
#> Trackway_15 21.518429
#> Trackway_16 13.553252
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[90]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 8.877697 16.267366 5.524663 8.787981
#> Trackway_02 8.877697 NA 6.574714 5.339129 5.123412
#> Trackway_03 16.267366 6.574714 NA 13.490155 3.545808
#> Trackway_04 5.524663 5.339129 13.490155 NA 8.246824
#> Trackway_07 8.787981 5.123412 3.545808 8.246824 NA
#> Trackway_08 12.416798 5.009341 2.206117 10.354917 1.877032
#> Trackway_09 13.351321 3.647671 3.230850 9.779015 5.414111
#> Trackway_13 8.733688 2.690633 3.912905 5.691475 2.427253
#> Trackway_15 45.248399 35.751576 21.628494 46.085000 22.928349
#> Trackway_16 35.513358 27.717724 14.699414 37.410383 14.180836
#> Trackway_18 14.696437 5.610219 1.527588 12.421161 3.001621
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 12.416798 13.351321 8.733688 45.24840 35.51336
#> Trackway_02 5.009341 3.647671 2.690633 35.75158 27.71772
#> Trackway_03 2.206117 3.230850 3.912905 21.62849 14.69941
#> Trackway_04 10.354917 9.779015 5.691475 46.08500 37.41038
#> Trackway_07 1.877032 5.414111 2.427253 22.92835 14.18084
#> Trackway_08 NA 3.610415 2.331885 21.37323 13.32093
#> Trackway_09 3.610415 NA 3.795035 29.18493 22.10119
#> Trackway_13 2.331885 3.795035 NA 27.34918 19.14158
#> Trackway_15 21.373226 29.184927 27.349183 NA 12.24743
#> Trackway_16 13.320927 22.101195 19.141579 12.24743 NA
#> Trackway_18 1.194464 2.890788 3.269331 20.70777 13.30439
#> Trackway_18
#> Trackway_01 14.696437
#> Trackway_02 5.610219
#> Trackway_03 1.527588
#> Trackway_04 12.421161
#> Trackway_07 3.001621
#> Trackway_08 1.194464
#> Trackway_09 2.890788
#> Trackway_13 3.269331
#> Trackway_15 20.707767
#> Trackway_16 13.304391
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[91]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 12.150759 18.434601 7.441556 13.686744
#> Trackway_02 12.150759 NA 8.019544 8.289466 4.900178
#> Trackway_03 18.434601 8.019544 NA 17.246940 2.526773
#> Trackway_04 7.441556 8.289466 17.246940 NA 12.079549
#> Trackway_07 13.686744 4.900178 2.526773 12.079549 NA
#> Trackway_08 15.183818 6.412339 1.628386 14.198042 1.999107
#> Trackway_09 19.359647 9.156299 2.177271 18.604976 4.697075
#> Trackway_13 15.535631 4.590040 2.397183 12.989997 2.435979
#> Trackway_15 43.111547 38.063142 21.496554 47.809250 23.197113
#> Trackway_16 31.059891 28.813093 13.890541 36.748551 14.189685
#> Trackway_18 16.294892 7.000924 1.245710 15.267722 2.289177
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 15.1838180 19.359647 15.535631 43.11155 31.05989
#> Trackway_02 6.4123392 9.156299 4.590040 38.06314 28.81309
#> Trackway_03 1.6283863 2.177271 2.397183 21.49655 13.89054
#> Trackway_04 14.1980419 18.604976 12.989997 47.80925 36.74855
#> Trackway_07 1.9991073 4.697075 2.435979 23.19711 14.18969
#> Trackway_08 NA 3.742354 2.291277 21.25100 12.70756
#> Trackway_09 3.7423542 NA 3.765989 26.22962 19.09895
#> Trackway_13 2.2912767 3.765989 NA 27.09931 18.77330
#> Trackway_15 21.2510018 26.229622 27.099312 NA 13.76126
#> Trackway_16 12.7075559 19.098951 18.773305 13.76126 NA
#> Trackway_18 0.5240517 3.115860 2.319144 21.01812 12.81115
#> Trackway_18
#> Trackway_01 16.2948919
#> Trackway_02 7.0009240
#> Trackway_03 1.2457097
#> Trackway_04 15.2677223
#> Trackway_07 2.2891771
#> Trackway_08 0.5240517
#> Trackway_09 3.1158599
#> Trackway_13 2.3191440
#> Trackway_15 21.0181243
#> Trackway_16 12.8111530
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[92]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 5.435560 18.875587 12.950914 10.378801
#> Trackway_02 5.43556 NA 12.011256 7.938397 5.641933
#> Trackway_03 18.87559 12.011256 NA 13.526735 3.980933
#> Trackway_04 12.95091 7.938397 13.526735 NA 9.711708
#> Trackway_07 10.37880 5.641933 3.980933 9.711708 NA
#> Trackway_08 12.79206 7.182806 3.104332 10.381078 1.089231
#> Trackway_09 13.62080 7.460704 3.891479 8.690015 3.613109
#> Trackway_13 14.82460 8.315378 2.863455 7.307260 4.137365
#> Trackway_15 42.84005 36.259789 19.825187 45.251175 20.563470
#> Trackway_16 33.31619 27.787550 14.248080 38.578304 12.700890
#> Trackway_18 15.93646 9.559575 1.786699 11.783872 2.558117
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 12.792063 13.620796 14.824597 42.84005 33.31619
#> Trackway_02 7.182806 7.460704 8.315378 36.25979 27.78755
#> Trackway_03 3.104332 3.891479 2.863455 19.82519 14.24808
#> Trackway_04 10.381078 8.690015 7.307260 45.25118 38.57830
#> Trackway_07 1.089231 3.613109 4.137365 20.56347 12.70089
#> Trackway_08 NA 2.803993 3.436713 19.88953 12.52682
#> Trackway_09 2.803993 NA 2.358371 26.39992 19.74022
#> Trackway_13 3.436713 2.358371 NA 25.47226 19.08565
#> Trackway_15 19.889529 26.399915 25.472259 NA 11.75109
#> Trackway_16 12.526816 19.740224 19.085653 11.75109 NA
#> Trackway_18 1.621035 2.388870 2.359282 19.23941 12.82987
#> Trackway_18
#> Trackway_01 15.936463
#> Trackway_02 9.559575
#> Trackway_03 1.786699
#> Trackway_04 11.783872
#> Trackway_07 2.558117
#> Trackway_08 1.621035
#> Trackway_09 2.388870
#> Trackway_13 2.359282
#> Trackway_15 19.239405
#> Trackway_16 12.829872
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[93]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 6.235637 10.598757 3.794082 5.623094
#> Trackway_02 6.235637 NA 5.648676 3.887109 6.610548
#> Trackway_03 10.598757 5.648676 NA 10.297424 3.355950
#> Trackway_04 3.794082 3.887109 10.297424 NA 8.069317
#> Trackway_07 5.623094 6.610548 3.355950 8.069317 NA
#> Trackway_08 10.354072 6.064686 1.633493 10.539475 3.086880
#> Trackway_09 10.814867 5.735326 2.233367 10.185589 5.740015
#> Trackway_13 4.407665 5.402880 3.860232 6.238536 2.310357
#> Trackway_15 42.032230 35.011606 21.150930 43.035830 22.827025
#> Trackway_16 33.932847 28.481033 14.463503 35.918064 14.238640
#> Trackway_18 9.946741 5.982828 1.283562 10.093122 3.071809
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 10.354072 10.814867 4.407665 42.03223 33.93285
#> Trackway_02 6.064686 5.735326 5.402880 35.01161 28.48103
#> Trackway_03 1.633493 2.233367 3.860232 21.15093 14.46350
#> Trackway_04 10.539475 10.185589 6.238536 43.03583 35.91806
#> Trackway_07 3.086880 5.740015 2.310357 22.82702 14.23864
#> Trackway_08 NA 2.909604 3.241700 20.13211 12.88118
#> Trackway_09 2.909604 NA 4.844678 25.45451 19.30351
#> Trackway_13 3.241700 4.844678 NA 26.59880 18.45745
#> Trackway_15 20.132107 25.454509 26.598799 NA 12.92291
#> Trackway_16 12.881179 19.303513 18.457446 12.92291 NA
#> Trackway_18 0.583053 2.856217 3.141354 20.39580 13.31311
#> Trackway_18
#> Trackway_01 9.946741
#> Trackway_02 5.982828
#> Trackway_03 1.283562
#> Trackway_04 10.093122
#> Trackway_07 3.071809
#> Trackway_08 0.583053
#> Trackway_09 2.856217
#> Trackway_13 3.141354
#> Trackway_15 20.395804
#> Trackway_16 13.313107
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[94]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1.991373 13.959711 3.774133 7.541225
#> Trackway_02 1.991373 NA 10.787758 5.030806 5.037463
#> Trackway_03 13.959711 10.787758 NA 13.596580 3.251922
#> Trackway_04 3.774133 5.030806 13.596580 NA 8.399810
#> Trackway_07 7.541225 5.037463 3.251922 8.399810 NA
#> Trackway_08 8.916325 5.565030 3.796737 9.753657 1.190292
#> Trackway_09 6.319000 4.230368 5.383012 7.267745 2.122368
#> Trackway_13 11.436638 8.839494 2.142169 10.434480 3.888495
#> Trackway_15 42.182511 35.085051 20.267243 43.668159 21.349743
#> Trackway_16 33.108762 25.876537 14.224023 35.592110 13.201826
#> Trackway_18 12.290621 8.877430 1.708207 12.541629 2.152188
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 8.916325 6.319000 11.436638 42.18251 33.10876
#> Trackway_02 5.565030 4.230368 8.839494 35.08505 25.87654
#> Trackway_03 3.796737 5.383012 2.142169 20.26724 14.22402
#> Trackway_04 9.753657 7.267745 10.434480 43.66816 35.59211
#> Trackway_07 1.190292 2.122368 3.888495 21.34974 13.20183
#> Trackway_08 NA 2.873529 4.712988 20.60848 12.12701
#> Trackway_09 2.873529 NA 4.474202 27.66202 19.55257
#> Trackway_13 4.712988 4.474202 NA 25.09086 18.76346
#> Trackway_15 20.608483 27.662024 25.090858 NA 13.09945
#> Trackway_16 12.127007 19.552572 18.763464 13.09945 NA
#> Trackway_18 2.301346 3.951428 2.224697 19.69957 12.74948
#> Trackway_18
#> Trackway_01 12.290621
#> Trackway_02 8.877430
#> Trackway_03 1.708207
#> Trackway_04 12.541629
#> Trackway_07 2.152188
#> Trackway_08 2.301346
#> Trackway_09 3.951428
#> Trackway_13 2.224697
#> Trackway_15 19.699568
#> Trackway_16 12.749485
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[95]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 11.766630 16.847193 21.994051 8.444898
#> Trackway_02 11.766630 NA 5.503690 10.149862 5.735222
#> Trackway_03 16.847193 5.503690 NA 8.967855 3.878372
#> Trackway_04 21.994051 10.149862 8.967855 NA 16.987275
#> Trackway_07 8.444898 5.735222 3.878372 16.987275 NA
#> Trackway_08 12.441147 4.425272 2.331942 13.842287 2.160651
#> Trackway_09 12.075764 3.544963 3.367984 11.917601 4.189082
#> Trackway_13 14.104136 2.912832 2.067902 9.270894 4.408411
#> Trackway_15 44.069448 35.172858 21.677300 42.475720 23.185499
#> Trackway_16 32.380878 26.165843 13.417470 36.094435 12.870757
#> Trackway_18 19.120309 7.698458 1.459366 8.726105 4.937036
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 12.441147 12.075764 14.104136 44.06945 32.38088
#> Trackway_02 4.425272 3.544963 2.912832 35.17286 26.16584
#> Trackway_03 2.331942 3.367984 2.067902 21.67730 13.41747
#> Trackway_04 13.842287 11.917601 9.270894 42.47572 36.09443
#> Trackway_07 2.160651 4.189082 4.408411 23.18550 12.87076
#> Trackway_08 NA 2.555661 2.593362 21.43179 11.92186
#> Trackway_09 2.555661 NA 2.575222 28.30206 19.07989
#> Trackway_13 2.593362 2.575222 NA 26.77328 18.05360
#> Trackway_15 21.431795 28.302059 26.773276 NA 13.11686
#> Trackway_16 11.921860 19.079894 18.053600 13.11686 NA
#> Trackway_18 3.013574 4.481997 3.588369 20.35107 12.69573
#> Trackway_18
#> Trackway_01 19.120309
#> Trackway_02 7.698458
#> Trackway_03 1.459366
#> Trackway_04 8.726105
#> Trackway_07 4.937036
#> Trackway_08 3.013574
#> Trackway_09 4.481997
#> Trackway_13 3.588369
#> Trackway_15 20.351070
#> Trackway_16 12.695734
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[96]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 3.720172 11.1060860 7.792903 7.121719
#> Trackway_02 3.720172 NA 9.7345281 6.335565 3.523388
#> Trackway_03 11.106086 9.734528 NA 18.454383 4.591920
#> Trackway_04 7.792903 6.335565 18.4543830 NA 9.488340
#> Trackway_07 7.121719 3.523388 4.5919198 9.488340 NA
#> Trackway_08 9.180252 5.125694 4.4890360 11.137205 1.487531
#> Trackway_09 6.945327 6.421893 3.4002192 14.211422 5.405712
#> Trackway_13 10.523460 9.644254 1.6049950 18.060508 6.829638
#> Trackway_15 43.353077 35.919765 21.1388817 47.716235 23.454610
#> Trackway_16 33.726050 25.640347 13.4549988 36.717838 13.066219
#> Trackway_18 9.960035 8.561781 0.9844686 16.929444 4.017727
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 9.180252 6.945327 10.523460 43.35308 33.72605
#> Trackway_02 5.125694 6.421893 9.644254 35.91977 25.64035
#> Trackway_03 4.489036 3.400219 1.604995 21.13888 13.45500
#> Trackway_04 11.137205 14.211422 18.060508 47.71624 36.71784
#> Trackway_07 1.487531 5.405712 6.829638 23.45461 13.06622
#> Trackway_08 NA 5.775908 6.983802 22.11316 11.63931
#> Trackway_09 5.775908 NA 3.676837 28.03007 19.55936
#> Trackway_13 6.983802 3.676837 NA 26.15211 18.93350
#> Trackway_15 22.113160 28.030073 26.152108 NA 13.80301
#> Trackway_16 11.639308 19.559359 18.933501 13.80301 NA
#> Trackway_18 3.711612 3.063217 2.763279 20.86982 12.72589
#> Trackway_18
#> Trackway_01 9.9600349
#> Trackway_02 8.5617805
#> Trackway_03 0.9844686
#> Trackway_04 16.9294441
#> Trackway_07 4.0177269
#> Trackway_08 3.7116125
#> Trackway_09 3.0632172
#> Trackway_13 2.7632792
#> Trackway_15 20.8698201
#> Trackway_16 12.7258920
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[97]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 3.897038 13.820551 4.516370 5.393386
#> Trackway_02 3.897038 NA 8.263433 4.208609 5.236632
#> Trackway_03 13.820551 8.263433 NA 14.400246 5.166114
#> Trackway_04 4.516370 4.208609 14.400246 NA 8.185830
#> Trackway_07 5.393386 5.236632 5.166114 8.185830 NA
#> Trackway_08 7.662164 5.945093 4.118803 9.788873 2.024013
#> Trackway_09 10.490403 5.062755 2.930241 10.337503 6.349280
#> Trackway_13 6.267374 2.802817 4.732374 6.276866 3.434573
#> Trackway_15 42.353193 35.701148 20.605128 45.695422 23.711017
#> Trackway_16 31.856217 26.080882 13.233258 35.851978 13.369223
#> Trackway_18 13.056027 7.571722 0.549741 13.639082 4.901586
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 7.662164 10.490403 6.267374 42.35319 31.85622
#> Trackway_02 5.945093 5.062755 2.802817 35.70115 26.08088
#> Trackway_03 4.118803 2.930241 4.732374 20.60513 13.23326
#> Trackway_04 9.788873 10.337503 6.276866 45.69542 35.85198
#> Trackway_07 2.024013 6.349280 3.434573 23.71102 13.36922
#> Trackway_08 NA 5.868707 3.409981 21.70581 11.65370
#> Trackway_09 5.868707 NA 3.696127 28.32629 20.41313
#> Trackway_13 3.409981 3.696127 NA 27.59335 18.37363
#> Trackway_15 21.705810 28.326286 27.593354 NA 13.79278
#> Trackway_16 11.653699 20.413135 18.373630 13.79278 NA
#> Trackway_18 3.740290 2.529988 4.402535 20.40826 12.79641
#> Trackway_18
#> Trackway_01 13.056027
#> Trackway_02 7.571722
#> Trackway_03 0.549741
#> Trackway_04 13.639082
#> Trackway_07 4.901586
#> Trackway_08 3.740290
#> Trackway_09 2.529988
#> Trackway_13 4.402535
#> Trackway_15 20.408257
#> Trackway_16 12.796411
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[98]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 2.658871 12.914231 3.414885 6.151374
#> Trackway_02 2.658871 NA 8.606883 3.970897 3.653546
#> Trackway_03 12.914231 8.606883 NA 14.787235 3.774523
#> Trackway_04 3.414885 3.970897 14.787235 NA 8.057255
#> Trackway_07 6.151374 3.653546 3.774523 8.057255 NA
#> Trackway_08 8.931250 5.216645 2.336039 10.474869 1.914782
#> Trackway_09 9.673220 6.345293 2.997507 11.876071 3.647375
#> Trackway_13 12.853029 8.734751 1.852724 14.735636 5.661490
#> Trackway_15 44.686469 38.286770 21.941306 47.791672 24.536797
#> Trackway_16 32.542895 26.493957 12.117751 35.366391 12.716063
#> Trackway_18 8.175770 4.907521 2.536171 9.789458 1.605975
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 8.9312499 9.673220 12.853029 44.68647 32.54289
#> Trackway_02 5.2166449 6.345293 8.734751 38.28677 26.49396
#> Trackway_03 2.3360388 2.997507 1.852724 21.94131 12.11775
#> Trackway_04 10.4748692 11.876071 14.735636 47.79167 35.36639
#> Trackway_07 1.9147820 3.647375 5.661490 24.53680 12.71606
#> Trackway_08 NA 2.602817 4.551512 22.70671 11.40494
#> Trackway_09 2.6028174 NA 3.637795 28.10281 17.51252
#> Trackway_13 4.5515122 3.637795 NA 27.37725 18.03394
#> Trackway_15 22.7067121 28.102815 27.377246 NA 14.82700
#> Trackway_16 11.4049419 17.512521 18.033936 14.82700 NA
#> Trackway_18 0.5772878 3.011425 4.812504 23.00861 11.61433
#> Trackway_18
#> Trackway_01 8.1757703
#> Trackway_02 4.9075215
#> Trackway_03 2.5361714
#> Trackway_04 9.7894583
#> Trackway_07 1.6059745
#> Trackway_08 0.5772878
#> Trackway_09 3.0114246
#> Trackway_13 4.8125042
#> Trackway_15 23.0086146
#> Trackway_16 11.6143306
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[99]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 10.025462 18.8904043 4.231985 8.122473
#> Trackway_02 10.025462 NA 8.9721305 6.679890 6.666952
#> Trackway_03 18.890404 8.972131 NA 17.023286 5.105936
#> Trackway_04 4.231985 6.679890 17.0232855 NA 8.054909
#> Trackway_07 8.122473 6.666952 5.1059364 8.054909 NA
#> Trackway_08 10.261795 6.156301 4.0850653 9.828511 1.421305
#> Trackway_09 12.451549 3.911278 4.7588979 10.504722 3.756450
#> Trackway_13 13.095191 3.790692 3.8518465 10.470253 4.445880
#> Trackway_15 45.416974 37.828393 21.4962536 46.005666 23.817361
#> Trackway_16 32.409030 27.189971 12.9976963 33.955113 12.036087
#> Trackway_18 19.565469 9.477463 0.4885352 17.677143 5.252670
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 10.261795 12.451549 13.095191 45.41697 32.40903
#> Trackway_02 6.156301 3.911278 3.790692 37.82839 27.18997
#> Trackway_03 4.085065 4.758898 3.851847 21.49625 12.99770
#> Trackway_04 9.828511 10.504722 10.470253 46.00567 33.95511
#> Trackway_07 1.421305 3.756450 4.445880 23.81736 12.03609
#> Trackway_08 NA 2.890472 3.587710 22.50798 11.22946
#> Trackway_09 2.890472 NA 2.608218 27.17390 16.79625
#> Trackway_13 3.587710 2.608218 NA 27.63703 17.69967
#> Trackway_15 22.507984 27.173898 27.637035 NA 15.00016
#> Trackway_16 11.229459 16.796254 17.699668 15.00016 NA
#> Trackway_18 4.134611 4.923624 4.184864 21.06425 12.66809
#> Trackway_18
#> Trackway_01 19.5654687
#> Trackway_02 9.4774632
#> Trackway_03 0.4885352
#> Trackway_04 17.6771426
#> Trackway_07 5.2526702
#> Trackway_08 4.1346108
#> Trackway_09 4.9236245
#> Trackway_13 4.1848636
#> Trackway_15 21.0642546
#> Trackway_16 12.6680854
#> Trackway_18 NA
#>
#> $DTW_distance_metric_simulations[[100]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 13.463669 20.999902 9.545644 11.438556
#> Trackway_02 13.463669 NA 8.710855 6.043233 5.098743
#> Trackway_03 20.999902 8.710855 NA 16.681479 4.641481
#> Trackway_04 9.545644 6.043233 16.681479 NA 7.493994
#> Trackway_07 11.438556 5.098743 4.641481 7.493994 NA
#> Trackway_08 16.022759 5.401124 2.909476 11.713320 2.595876
#> Trackway_09 17.360120 6.180204 2.985789 13.099442 4.802784
#> Trackway_13 15.499186 3.265798 4.309973 9.111740 3.244858
#> Trackway_15 42.859691 36.091810 21.131588 45.622752 22.590705
#> Trackway_16 31.059588 27.394559 14.557198 35.545438 13.247926
#> Trackway_18 16.231543 5.430575 2.780460 11.839828 2.640796
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 16.0227594 17.360120 15.499186 42.85969 31.05959
#> Trackway_02 5.4011237 6.180204 3.265798 36.09181 27.39456
#> Trackway_03 2.9094762 2.985789 4.309973 21.13159 14.55720
#> Trackway_04 11.7133204 13.099442 9.111740 45.62275 35.54544
#> Trackway_07 2.5958761 4.802784 3.244858 22.59070 13.24793
#> Trackway_08 NA 2.621309 2.742818 20.44671 12.31514
#> Trackway_09 2.6213089 NA 3.431150 25.82231 18.25520
#> Trackway_13 2.7428180 3.431150 NA 26.95422 18.80959
#> Trackway_15 20.4467138 25.822314 26.954217 NA 13.18614
#> Trackway_16 12.3151389 18.255198 18.809589 13.18614 NA
#> Trackway_18 0.4557425 2.366763 2.525145 20.53113 12.45904
#> Trackway_18
#> Trackway_01 16.2315434
#> Trackway_02 5.4305751
#> Trackway_03 2.7804604
#> Trackway_04 11.8398277
#> Trackway_07 2.6407959
#> Trackway_08 0.4557425
#> Trackway_09 2.3667631
#> Trackway_13 2.5251448
#> Trackway_15 20.5311279
#> Trackway_16 12.4590411
#> Trackway_18 NA
simil_frechet_constrained_mount <- simil_Frechet_metric(sbMountTom, test = TRUE,
sim = sim_constrained_mount,
superposition = "Origin")#> $Frechet_distance_metric
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1.160390 2.4945901 3.1337951 2.7855204
#> Trackway_02 1.160390 NA 3.0295676 3.5610723 2.9120089
#> Trackway_03 2.494590 3.029568 NA 0.6990308 1.0052681
#> Trackway_04 3.133795 3.561072 0.6990308 NA 0.8725870
#> Trackway_07 2.785520 2.912009 1.0052681 0.8725870 NA
#> Trackway_08 2.269127 2.323426 1.3825382 1.3675584 0.7159497
#> Trackway_09 -1.000000 -1.000000 -1.0000000 8.6824063 -1.0000000
#> Trackway_13 -1.000000 -1.000000 5.0934012 -1.0000000 5.5973926
#> Trackway_15 3.488624 3.717395 1.4162175 0.9587033 0.9391911
#> Trackway_16 1.475156 1.269154 1.9329666 2.3337292 1.6487147
#> Trackway_18 3.689199 4.322800 1.7095695 1.1977112 0.9307631
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 2.2691267 -1.000000 -1.000000 3.4886244 1.475156
#> Trackway_02 2.3234259 -1.000000 -1.000000 3.7173953 1.269154
#> Trackway_03 1.3825382 -1.000000 5.093401 1.4162175 1.932967
#> Trackway_04 1.3675584 8.682406 -1.000000 0.9587033 2.333729
#> Trackway_07 0.7159497 -1.000000 5.597393 0.9391911 1.648715
#> Trackway_08 NA -1.000000 -1.000000 1.3556652 1.056683
#> Trackway_09 -1.0000000 NA -1.000000 8.4868925 10.898587
#> Trackway_13 -1.0000000 -1.000000 NA -1.0000000 7.018274
#> Trackway_15 1.3556652 8.486892 -1.000000 NA 2.412239
#> Trackway_16 1.0566835 10.898587 7.018274 2.4122388 NA
#> Trackway_18 1.4465877 -1.000000 -1.000000 0.4602478 2.475047
#> Trackway_18
#> Trackway_01 3.6891994
#> Trackway_02 4.3228000
#> Trackway_03 1.7095695
#> Trackway_04 1.1977112
#> Trackway_07 0.9307631
#> Trackway_08 1.4465877
#> Trackway_09 -1.0000000
#> Trackway_13 -1.0000000
#> Trackway_15 0.4602478
#> Trackway_16 2.4750475
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_p_values
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0.30693069 0.02970297 0.87128713 0.67326733
#> Trackway_02 0.30693069 NA 0.85148515 0.98019802 0.99009901
#> Trackway_03 0.02970297 0.85148515 NA 0.00990099 0.03960396
#> Trackway_04 0.87128713 0.98019802 0.00990099 NA 0.00990099
#> Trackway_07 0.67326733 0.99009901 0.03960396 0.00990099 NA
#> Trackway_08 0.00990099 0.26732673 0.60396040 0.00990099 0.26732673
#> Trackway_09 0.00990099 0.00990099 0.00990099 1.00000000 0.00990099
#> Trackway_13 0.00990099 0.00990099 1.00000000 0.00990099 1.00000000
#> Trackway_15 0.43564356 0.41584158 0.40594059 0.37623762 0.41584158
#> Trackway_16 0.25742574 0.31683168 0.40594059 0.27722772 0.34653465
#> Trackway_18 0.62376238 0.99009901 0.98019802 0.00990099 0.18811881
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0.00990099 0.00990099 0.00990099 0.4356436 0.2574257
#> Trackway_02 0.26732673 0.00990099 0.00990099 0.4158416 0.3168317
#> Trackway_03 0.60396040 0.00990099 1.00000000 0.4059406 0.4059406
#> Trackway_04 0.00990099 1.00000000 0.00990099 0.3762376 0.2772277
#> Trackway_07 0.26732673 0.00990099 1.00000000 0.4158416 0.3465347
#> Trackway_08 NA 0.00990099 0.00990099 0.4059406 0.2376238
#> Trackway_09 0.00990099 NA 0.00990099 0.4059406 1.0000000
#> Trackway_13 0.00990099 0.00990099 NA 0.4851485 1.0000000
#> Trackway_15 0.40594059 0.40594059 0.48514851 NA 0.4158416
#> Trackway_16 0.23762376 1.00000000 1.00000000 0.4158416 NA
#> Trackway_18 0.73267327 0.00990099 0.00990099 0.3465347 0.4554455
#> Trackway_18
#> Trackway_01 0.62376238
#> Trackway_02 0.99009901
#> Trackway_03 0.98019802
#> Trackway_04 0.00990099
#> Trackway_07 0.18811881
#> Trackway_08 0.73267327
#> Trackway_09 0.00990099
#> Trackway_13 0.00990099
#> Trackway_15 0.34653465
#> Trackway_16 0.45544554
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_p_values_BH
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0.61814290 0.09075908 1.00000000 0.86115588
#> Trackway_02 0.61814290 NA 1.00000000 1.00000000 1.00000000
#> Trackway_03 0.09075908 1.00000000 NA 0.03203262 0.11464304
#> Trackway_04 1.00000000 1.00000000 0.03203262 NA 0.03203262
#> Trackway_07 0.86115588 1.00000000 0.11464304 0.03203262 NA
#> Trackway_08 0.03203262 0.60990099 0.81019078 0.03203262 0.60990099
#> Trackway_09 0.03203262 0.03203262 0.03203262 1.00000000 0.03203262
#> Trackway_13 0.03203262 0.03203262 1.00000000 0.03203262 1.00000000
#> Trackway_15 0.63053674 0.61814290 0.61814290 0.61814290 0.61814290
#> Trackway_16 0.60990099 0.61814290 0.61814290 0.60990099 0.61814290
#> Trackway_18 0.81683168 1.00000000 1.00000000 0.03203262 0.51732673
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0.03203262 0.03203262 0.03203262 0.6305367 0.6099010
#> Trackway_02 0.60990099 0.03203262 0.03203262 0.6181429 0.6181429
#> Trackway_03 0.81019078 0.03203262 1.00000000 0.6181429 0.6181429
#> Trackway_04 0.03203262 1.00000000 0.03203262 0.6181429 0.6099010
#> Trackway_07 0.60990099 0.03203262 1.00000000 0.6181429 0.6181429
#> Trackway_08 NA 0.03203262 0.03203262 0.6181429 0.6099010
#> Trackway_09 0.03203262 NA 0.03203262 0.6181429 1.0000000
#> Trackway_13 0.03203262 0.03203262 NA 0.6670792 1.0000000
#> Trackway_15 0.61814290 0.61814290 0.66707921 NA 0.6181429
#> Trackway_16 0.60990099 1.00000000 1.00000000 0.6181429 NA
#> Trackway_18 0.91584158 0.03203262 0.03203262 0.6181429 0.6422950
#> Trackway_18
#> Trackway_01 0.81683168
#> Trackway_02 1.00000000
#> Trackway_03 1.00000000
#> Trackway_04 0.03203262
#> Trackway_07 0.51732673
#> Trackway_08 0.91584158
#> Trackway_09 0.03203262
#> Trackway_13 0.03203262
#> Trackway_15 0.61814290
#> Trackway_16 0.64229500
#> Trackway_18 NA
#>
#> $Frechet_metric_p_values_combined
#> [1] 0
#>
#> $Frechet_distance_metric_simulations
#> $Frechet_distance_metric_simulations[[1]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1.6208323 2.953733 0.9042469 2.0786598
#> Trackway_02 1.6208323 NA 1.954993 1.8862346 1.7923307
#> Trackway_03 2.9537329 1.9549927 NA 3.6276078 1.4858812
#> Trackway_04 0.9042469 1.8862346 3.627608 NA 2.8713840
#> Trackway_07 2.0786598 1.7923307 1.485881 2.8713840 NA
#> Trackway_08 2.8894367 2.1974459 1.070873 3.5128120 0.6964501
#> Trackway_09 1.9892205 2.0194954 1.404851 2.8434002 0.3980089
#> Trackway_13 2.1009403 0.7185171 1.226130 2.6146720 1.5109517
#> Trackway_15 11.2870428 10.3664807 8.488614 12.0689462 -1.0000000
#> Trackway_16 7.2666136 -1.0000000 5.373252 8.1650240 5.3491985
#> Trackway_18 2.4394784 2.0589334 1.224611 3.4205367 0.7134202
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 2.8894367 1.9892205 2.1009403 11.287043 7.266614
#> Trackway_02 2.1974459 2.0194954 0.7185171 10.366481 -1.000000
#> Trackway_03 1.0708728 1.4048505 1.2261303 8.488614 5.373252
#> Trackway_04 3.5128120 2.8434002 2.6146720 12.068946 8.165024
#> Trackway_07 0.6964501 0.3980089 1.5109517 -1.000000 5.349199
#> Trackway_08 NA 0.7587002 1.8519119 -1.000000 -1.000000
#> Trackway_09 0.7587002 NA 1.4571203 9.322684 5.384330
#> Trackway_13 1.8519119 1.4571203 NA -1.000000 6.431146
#> Trackway_15 -1.0000000 9.3226838 -1.0000000 NA -1.000000
#> Trackway_16 -1.0000000 5.3843302 6.4311456 -1.000000 NA
#> Trackway_18 0.8407443 0.4541322 1.6367498 -1.000000 4.980117
#> Trackway_18
#> Trackway_01 2.4394784
#> Trackway_02 2.0589334
#> Trackway_03 1.2246107
#> Trackway_04 3.4205367
#> Trackway_07 0.7134202
#> Trackway_08 0.8407443
#> Trackway_09 0.4541322
#> Trackway_13 1.6367498
#> Trackway_15 -1.0000000
#> Trackway_16 4.9801173
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[2]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1.787718 4.2455318 0.8630584 3.0161063
#> Trackway_02 1.7877177 NA 2.4071072 2.2494364 1.7499367
#> Trackway_03 4.2455318 2.407107 NA 4.5899180 1.0400048
#> Trackway_04 0.8630584 2.249436 4.5899180 NA 3.7371783
#> Trackway_07 3.0161063 1.749937 1.0400048 3.7371783 NA
#> Trackway_08 3.3464558 2.180577 1.0177332 4.1012532 0.4381037
#> Trackway_09 2.4868522 2.200906 2.4232709 3.3412751 1.4350533
#> Trackway_13 2.5156528 1.090084 1.9649910 3.3866879 0.9933210
#> Trackway_15 -1.0000000 -1.000000 8.2778109 -1.0000000 -1.0000000
#> Trackway_16 7.1852469 6.699397 5.1356518 8.0480405 -1.0000000
#> Trackway_18 3.6100946 2.348182 0.4077878 4.2552153 0.6327782
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.3464558 2.486852 2.515653 -1.000000 7.185247
#> Trackway_02 2.1805772 2.200906 1.090084 -1.000000 6.699397
#> Trackway_03 1.0177332 2.423271 1.964991 8.277811 5.135652
#> Trackway_04 4.1012532 3.341275 3.386688 -1.000000 8.048040
#> Trackway_07 0.4381037 1.435053 0.993321 -1.000000 -1.000000
#> Trackway_08 NA 1.435905 1.138753 8.513378 -1.000000
#> Trackway_09 1.4359048 NA 1.598522 -1.000000 4.734436
#> Trackway_13 1.1387534 1.598522 NA 9.542282 5.698377
#> Trackway_15 8.5133784 -1.000000 9.542282 NA -1.000000
#> Trackway_16 -1.0000000 4.734436 5.698377 -1.000000 NA
#> Trackway_18 0.6584981 2.025264 1.085151 8.502052 5.068075
#> Trackway_18
#> Trackway_01 3.6100946
#> Trackway_02 2.3481819
#> Trackway_03 0.4077878
#> Trackway_04 4.2552153
#> Trackway_07 0.6327782
#> Trackway_08 0.6584981
#> Trackway_09 2.0252638
#> Trackway_13 1.0851510
#> Trackway_15 8.5020521
#> Trackway_16 5.0680746
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[3]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0.8757569 4.143854 1.707065 2.3947323
#> Trackway_02 0.8757569 NA 3.165921 2.037960 1.5067893
#> Trackway_03 4.1438543 3.1659215 NA 5.023313 2.1590819
#> Trackway_04 1.7070648 2.0379596 5.023313 NA 2.9617933
#> Trackway_07 2.3947323 1.5067893 2.159082 2.961793 NA
#> Trackway_08 3.4940573 2.6576374 1.191017 4.170002 1.2355505
#> Trackway_09 2.5382416 1.6800094 1.546051 3.477352 0.6406353
#> Trackway_13 1.8610270 1.1684189 2.291233 2.735780 0.4661201
#> Trackway_15 11.5757802 10.7003354 -1.000000 12.006446 9.3054531
#> Trackway_16 7.6496320 -1.0000000 5.286356 7.490464 -1.0000000
#> Trackway_18 3.2328865 2.5623036 1.798950 3.824448 0.9476017
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.4940573 2.5382416 1.8610270 11.575780 7.649632
#> Trackway_02 2.6576374 1.6800094 1.1684189 10.700335 -1.000000
#> Trackway_03 1.1910168 1.5460513 2.2912329 -1.000000 5.286356
#> Trackway_04 4.1700022 3.4773524 2.7357797 12.006446 7.490464
#> Trackway_07 1.2355505 0.6406353 0.4661201 9.305453 -1.000000
#> Trackway_08 NA 0.9893800 1.6098496 -1.000000 4.684304
#> Trackway_09 0.9893800 NA 0.7477543 9.067879 -1.000000
#> Trackway_13 1.6098496 0.7477543 NA -1.000000 5.961824
#> Trackway_15 -1.0000000 9.0678789 -1.0000000 NA 5.355792
#> Trackway_16 4.6843041 -1.0000000 5.9618240 5.355792 NA
#> Trackway_18 0.4943816 0.9882832 1.3924105 -1.000000 -1.000000
#> Trackway_18
#> Trackway_01 3.2328865
#> Trackway_02 2.5623036
#> Trackway_03 1.7989502
#> Trackway_04 3.8244476
#> Trackway_07 0.9476017
#> Trackway_08 0.4943816
#> Trackway_09 0.9882832
#> Trackway_13 1.3924105
#> Trackway_15 -1.0000000
#> Trackway_16 -1.0000000
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[4]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0.5309995 2.9584559 2.373127 1.9769475
#> Trackway_02 0.5309995 NA 2.7569245 2.210701 1.5622396
#> Trackway_03 2.9584559 2.7569245 NA 4.600700 1.5541434
#> Trackway_04 2.3731268 2.2107012 4.6006998 NA 3.0895025
#> Trackway_07 1.9769475 1.5622396 1.5541434 3.089502 NA
#> Trackway_08 2.8047824 2.3928955 1.2192130 3.817926 0.8492692
#> Trackway_09 2.3975201 2.2145973 0.6162386 4.377239 1.3525581
#> Trackway_13 2.5650008 2.5522016 1.2674589 4.746263 2.1425324
#> Trackway_15 -1.0000000 11.3479842 8.6573159 12.921901 -1.0000000
#> Trackway_16 6.8921736 6.4252041 -1.0000000 7.234121 4.8990259
#> Trackway_18 3.0250801 2.5642224 1.3730391 3.989142 1.0174758
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 2.8047824 2.3975201 2.565001 -1.000000 6.892174
#> Trackway_02 2.3928955 2.2145973 2.552202 11.347984 6.425204
#> Trackway_03 1.2192130 0.6162386 1.267459 8.657316 -1.000000
#> Trackway_04 3.8179260 4.3772387 4.746263 12.921901 7.234121
#> Trackway_07 0.8492692 1.3525581 2.142532 -1.000000 4.899026
#> Trackway_08 NA 1.5937000 2.247042 -1.000000 4.107219
#> Trackway_09 1.5937000 NA 0.856346 9.233353 5.112735
#> Trackway_13 2.2470424 0.8563460 NA 9.359696 -1.000000
#> Trackway_15 -1.0000000 9.2333534 9.359696 NA 6.585296
#> Trackway_16 4.1072186 5.1127351 -1.000000 6.585296 NA
#> Trackway_18 0.1919066 1.5489329 2.399499 -1.000000 3.905776
#> Trackway_18
#> Trackway_01 3.0250801
#> Trackway_02 2.5642224
#> Trackway_03 1.3730391
#> Trackway_04 3.9891421
#> Trackway_07 1.0174758
#> Trackway_08 0.1919066
#> Trackway_09 1.5489329
#> Trackway_13 2.3994992
#> Trackway_15 -1.0000000
#> Trackway_16 3.9057762
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[5]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1.180991 3.4895537 1.066933 2.637680
#> Trackway_02 1.180991 NA 2.3169124 1.747385 1.702875
#> Trackway_03 3.489554 2.316912 NA 4.403260 1.631946
#> Trackway_04 1.066933 1.747385 4.4032598 NA 3.414859
#> Trackway_07 2.637680 1.702875 1.6319464 3.414859 NA
#> Trackway_08 3.990001 2.778493 0.4975269 4.705468 1.851884
#> Trackway_09 3.079990 1.904481 0.4230283 3.662789 1.424210
#> Trackway_13 2.878482 1.709541 0.8952394 3.166217 2.002479
#> Trackway_15 11.701228 -1.000000 -1.0000000 12.469248 9.111333
#> Trackway_16 7.080141 6.431570 -1.0000000 8.056321 4.750442
#> Trackway_18 4.351694 3.048129 0.7320103 4.667620 2.173555
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.9900006 3.0799895 2.8784815 11.701228 7.080141
#> Trackway_02 2.7784932 1.9044809 1.7095410 -1.000000 6.431570
#> Trackway_03 0.4975269 0.4230283 0.8952394 -1.000000 -1.000000
#> Trackway_04 4.7054677 3.6627894 3.1662170 12.469248 8.056321
#> Trackway_07 1.8518843 1.4242096 2.0024786 9.111333 4.750442
#> Trackway_08 NA 0.9018436 1.3827041 -1.000000 5.036246
#> Trackway_09 0.9018436 NA 0.5877228 9.097500 5.529686
#> Trackway_13 1.3827041 0.5877228 NA -1.000000 -1.000000
#> Trackway_15 -1.0000000 9.0975003 -1.0000000 NA 5.621396
#> Trackway_16 5.0362458 5.5296856 -1.0000000 5.621396 NA
#> Trackway_18 0.3218144 1.1469887 1.5508876 -1.000000 -1.000000
#> Trackway_18
#> Trackway_01 4.3516936
#> Trackway_02 3.0481290
#> Trackway_03 0.7320103
#> Trackway_04 4.6676196
#> Trackway_07 2.1735547
#> Trackway_08 0.3218144
#> Trackway_09 1.1469887
#> Trackway_13 1.5508876
#> Trackway_15 -1.0000000
#> Trackway_16 -1.0000000
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[6]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 3.4926126 4.6584256 3.763282 2.7189003
#> Trackway_02 3.492613 NA 2.2836025 1.508155 1.9508723
#> Trackway_03 4.658426 2.2836025 NA 3.677430 1.9917114
#> Trackway_04 3.763282 1.5081552 3.6774298 NA 3.4190926
#> Trackway_07 2.718900 1.9508723 1.9917114 3.419093 NA
#> Trackway_08 3.083107 2.3366536 1.8416337 3.717141 0.5133304
#> Trackway_09 3.463587 1.4846640 1.2166592 2.903278 0.9443253
#> Trackway_13 3.654488 0.6613178 1.5561231 2.162106 1.6044900
#> Trackway_15 11.783904 -1.0000000 8.2856945 11.962739 9.4123748
#> Trackway_16 7.120547 7.2975001 -1.0000000 8.747235 5.5351384
#> Trackway_18 4.633280 2.2537006 0.2276131 4.119503 1.8052942
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.0831074 3.4635874 3.6544877 11.783904 7.120547
#> Trackway_02 2.3366536 1.4846640 0.6613178 -1.000000 7.297500
#> Trackway_03 1.8416337 1.2166592 1.5561231 8.285695 -1.000000
#> Trackway_04 3.7171406 2.9032784 2.1621065 11.962739 8.747235
#> Trackway_07 0.5133304 0.9443253 1.6044900 9.412375 5.535138
#> Trackway_08 NA 1.0768073 1.8843777 8.918510 -1.000000
#> Trackway_09 1.0768073 NA 0.8455619 9.229417 5.890198
#> Trackway_13 1.8843777 0.8455619 NA -1.000000 6.719709
#> Trackway_15 8.9185101 9.2294171 -1.0000000 NA 5.555590
#> Trackway_16 -1.0000000 5.8901980 6.7197089 5.555590 NA
#> Trackway_18 1.6859321 1.0928580 1.5533872 -1.000000 -1.000000
#> Trackway_18
#> Trackway_01 4.6332801
#> Trackway_02 2.2537006
#> Trackway_03 0.2276131
#> Trackway_04 4.1195033
#> Trackway_07 1.8052942
#> Trackway_08 1.6859321
#> Trackway_09 1.0928580
#> Trackway_13 1.5533872
#> Trackway_15 -1.0000000
#> Trackway_16 -1.0000000
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[7]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1.7452542 3.8076318 2.144668 2.5685035
#> Trackway_02 1.745254 NA 2.3516269 1.529030 2.0673362
#> Trackway_03 3.807632 2.3516269 NA 3.808119 1.7662396
#> Trackway_04 2.144668 1.5290300 3.8081195 NA 3.4051416
#> Trackway_07 2.568503 2.0673362 1.7662396 3.405142 NA
#> Trackway_08 3.580893 2.4516392 0.8379953 3.897282 1.2496174
#> Trackway_09 2.696770 1.9975540 1.7295399 3.524582 0.4144767
#> Trackway_13 2.263388 0.8060263 1.6950449 2.445807 1.2496174
#> Trackway_15 11.597935 10.3739408 -1.0000000 11.650636 9.0472504
#> Trackway_16 7.128213 -1.0000000 4.6416821 -1.000000 4.6732662
#> Trackway_18 4.165993 2.5164822 0.9894465 3.674118 2.0036674
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.5808932 2.6967697 2.2633877 11.597935 7.128213
#> Trackway_02 2.4516392 1.9975540 0.8060263 10.373941 -1.000000
#> Trackway_03 0.8379953 1.7295399 1.6950449 -1.000000 4.641682
#> Trackway_04 3.8972819 3.5245815 2.4458065 11.650636 -1.000000
#> Trackway_07 1.2496174 0.4144767 1.2496174 9.047250 4.673266
#> Trackway_08 NA 1.2244256 1.6230541 -1.000000 -1.000000
#> Trackway_09 1.2244256 NA 1.4826798 8.924543 4.531455
#> Trackway_13 1.6230541 1.4826798 NA 9.636209 -1.000000
#> Trackway_15 -1.0000000 8.9245426 9.6362085 NA 5.385142
#> Trackway_16 -1.0000000 4.5314552 -1.0000000 5.385142 NA
#> Trackway_18 1.1798327 2.0518534 1.8533456 7.979119 -1.000000
#> Trackway_18
#> Trackway_01 4.1659926
#> Trackway_02 2.5164822
#> Trackway_03 0.9894465
#> Trackway_04 3.6741181
#> Trackway_07 2.0036674
#> Trackway_08 1.1798327
#> Trackway_09 2.0518534
#> Trackway_13 1.8533456
#> Trackway_15 7.9791189
#> Trackway_16 -1.0000000
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[8]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1.156769 3.8709305 0.9049427 2.348030
#> Trackway_02 1.1567693 NA 2.9668587 1.6670992 2.377055
#> Trackway_03 3.8709305 2.966859 NA 4.9659252 2.916918
#> Trackway_04 0.9049427 1.667099 4.9659252 NA 3.213059
#> Trackway_07 2.3480296 2.377055 2.9169183 3.2130591 NA
#> Trackway_08 3.1424203 2.536003 1.1620997 4.1125678 1.622981
#> Trackway_09 3.7881235 2.881793 0.2080282 4.5251005 2.833172
#> Trackway_13 2.0505209 1.600356 2.0128796 2.8453265 1.196079
#> Trackway_15 11.5553033 11.130467 8.5522195 12.4337447 9.284382
#> Trackway_16 7.0344752 7.012781 -1.0000000 7.8737698 4.708398
#> Trackway_18 4.1159447 3.093344 0.3751549 4.6781792 2.562432
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.1424203 3.7881235 2.050521 11.555303 7.034475
#> Trackway_02 2.5360027 2.8817928 1.600356 11.130467 7.012781
#> Trackway_03 1.1620997 0.2080282 2.012880 8.552220 -1.000000
#> Trackway_04 4.1125678 4.5251005 2.845327 12.433745 7.873770
#> Trackway_07 1.6229814 2.8331725 1.196079 9.284382 4.708398
#> Trackway_08 NA 1.2623954 1.966730 8.600217 4.885556
#> Trackway_09 1.2623954 NA 2.022897 8.733417 5.747486
#> Trackway_13 1.9667304 2.0228968 NA -1.000000 5.602719
#> Trackway_15 8.6002169 8.7334170 -1.000000 NA -1.000000
#> Trackway_16 4.8855561 5.7474857 5.602719 -1.000000 NA
#> Trackway_18 0.9406677 0.5812839 1.985989 8.265838 -1.000000
#> Trackway_18
#> Trackway_01 4.1159447
#> Trackway_02 3.0933440
#> Trackway_03 0.3751549
#> Trackway_04 4.6781792
#> Trackway_07 2.5624321
#> Trackway_08 0.9406677
#> Trackway_09 0.5812839
#> Trackway_13 1.9859892
#> Trackway_15 8.2658382
#> Trackway_16 -1.0000000
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[9]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 2.073944 3.8648776 1.169348 2.621816
#> Trackway_02 2.073944 NA 2.6343536 1.436926 2.762613
#> Trackway_03 3.864878 2.634354 NA 3.529997 2.110851
#> Trackway_04 1.169348 1.436926 3.5299973 NA 2.817426
#> Trackway_07 2.621816 2.762613 2.1108512 2.817426 NA
#> Trackway_08 3.791404 2.906151 0.4041451 3.550428 1.802937
#> Trackway_09 3.924562 2.414091 0.7126505 3.463967 2.527269
#> Trackway_13 2.184051 1.702850 1.7164614 2.090760 1.095353
#> Trackway_15 -1.000000 -1.000000 -1.0000000 11.793634 -1.000000
#> Trackway_16 7.519868 7.592767 5.4611027 7.819112 5.002125
#> Trackway_18 4.514396 3.130235 0.8305000 4.127348 3.000797
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.7914038 3.9245619 2.184051 -1.000000 7.519868
#> Trackway_02 2.9061513 2.4140913 1.702850 -1.000000 7.592767
#> Trackway_03 0.4041451 0.7126505 1.716461 -1.000000 5.461103
#> Trackway_04 3.5504280 3.4639668 2.090760 11.793634 7.819112
#> Trackway_07 1.8029367 2.5272692 1.095353 -1.000000 5.002125
#> Trackway_08 NA 0.9708395 1.608009 8.309664 5.113787
#> Trackway_09 0.9708395 NA 1.905762 -1.000000 6.007282
#> Trackway_13 1.6080088 1.9057616 NA -1.000000 -1.000000
#> Trackway_15 8.3096640 -1.0000000 -1.000000 NA 5.372852
#> Trackway_16 5.1137870 6.0072824 -1.000000 5.372852 NA
#> Trackway_18 0.9473297 0.8662224 2.386484 8.060633 5.514139
#> Trackway_18
#> Trackway_01 4.5143962
#> Trackway_02 3.1302353
#> Trackway_03 0.8305000
#> Trackway_04 4.1273482
#> Trackway_07 3.0007974
#> Trackway_08 0.9473297
#> Trackway_09 0.8662224
#> Trackway_13 2.3864835
#> Trackway_15 8.0606333
#> Trackway_16 5.5141389
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[10]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1.8142198 3.9725701 0.8117215 2.550583
#> Trackway_02 1.8142198 NA 2.4092673 2.4340510 1.647952
#> Trackway_03 3.9725701 2.4092673 NA 4.6491476 1.738312
#> Trackway_04 0.8117215 2.4340510 4.6491476 NA 3.264428
#> Trackway_07 2.5505834 1.6479516 1.7383119 3.2644275 NA
#> Trackway_08 3.3592451 2.6226429 2.3016120 3.8085963 1.088557
#> Trackway_09 3.2224101 1.5458586 1.0244777 3.8626425 1.496103
#> Trackway_13 2.3499639 0.6641984 1.7268429 2.9830374 1.303645
#> Trackway_15 -1.0000000 -1.0000000 -1.0000000 -1.0000000 9.252477
#> Trackway_16 6.2977343 5.7681736 4.3689378 7.2258366 4.125112
#> Trackway_18 3.5477769 2.0211626 0.4379696 4.2705058 1.317076
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.359245 3.2224101 2.3499639 -1.000000 6.297734
#> Trackway_02 2.622643 1.5458586 0.6641984 -1.000000 5.768174
#> Trackway_03 2.301612 1.0244777 1.7268429 -1.000000 4.368938
#> Trackway_04 3.808596 3.8626425 2.9830374 -1.000000 7.225837
#> Trackway_07 1.088557 1.4961025 1.3036452 9.252477 4.125112
#> Trackway_08 NA 2.3675325 2.2563507 8.759938 3.240607
#> Trackway_09 2.367532 NA 0.8798567 9.225576 5.070078
#> Trackway_13 2.256351 0.8798567 NA 9.945135 5.412740
#> Trackway_15 8.759938 9.2255756 9.9451352 NA 6.209194
#> Trackway_16 3.240607 5.0700782 5.4127398 6.209194 NA
#> Trackway_18 2.073257 0.6914201 1.3580502 -1.000000 4.321619
#> Trackway_18
#> Trackway_01 3.5477769
#> Trackway_02 2.0211626
#> Trackway_03 0.4379696
#> Trackway_04 4.2705058
#> Trackway_07 1.3170764
#> Trackway_08 2.0732572
#> Trackway_09 0.6914201
#> Trackway_13 1.3580502
#> Trackway_15 -1.0000000
#> Trackway_16 4.3216193
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[11]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1.4799888 3.6008219 1.738341 2.4005705
#> Trackway_02 1.479989 NA 2.1604347 1.285536 1.7172582
#> Trackway_03 3.600822 2.1604347 NA 3.251129 1.6155013
#> Trackway_04 1.738341 1.2855359 3.2511289 NA 2.9995081
#> Trackway_07 2.400571 1.7172582 1.6155013 2.999508 NA
#> Trackway_08 2.715964 2.0747661 1.6133412 3.408664 0.8913939
#> Trackway_09 2.850922 1.5710914 0.6053767 2.719916 1.1837324
#> Trackway_13 1.900346 0.9760025 1.5958566 2.260709 0.9044635
#> Trackway_15 -1.000000 10.6094003 -1.0000000 -1.000000 -1.0000000
#> Trackway_16 6.873138 6.4885272 5.1482838 -1.000000 4.7724045
#> Trackway_18 2.783095 2.1121744 1.6134957 3.391885 0.4044500
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 2.7159643 2.8509223 1.9003459 -1.000000 6.873138
#> Trackway_02 2.0747661 1.5710914 0.9760025 10.609400 6.488527
#> Trackway_03 1.6133412 0.6053767 1.5958566 -1.000000 5.148284
#> Trackway_04 3.4086645 2.7199162 2.2607095 -1.000000 -1.000000
#> Trackway_07 0.8913939 1.1837324 0.9044635 -1.000000 4.772405
#> Trackway_08 NA 1.3335010 1.0990899 8.883582 4.413917
#> Trackway_09 1.3335010 NA 1.0171664 -1.000000 -1.000000
#> Trackway_13 1.0990899 1.0171664 NA 9.770729 -1.000000
#> Trackway_15 8.8835817 -1.0000000 9.7707291 NA 5.940527
#> Trackway_16 4.4139171 -1.0000000 -1.0000000 5.940527 NA
#> Trackway_18 0.1219174 1.2983583 1.1440472 -1.000000 -1.000000
#> Trackway_18
#> Trackway_01 2.7830950
#> Trackway_02 2.1121744
#> Trackway_03 1.6134957
#> Trackway_04 3.3918845
#> Trackway_07 0.4044500
#> Trackway_08 0.1219174
#> Trackway_09 1.2983583
#> Trackway_13 1.1440472
#> Trackway_15 -1.0000000
#> Trackway_16 -1.0000000
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[12]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 4.846162 5.120797 4.799061 3.5800838
#> Trackway_02 4.846162 NA 1.872957 1.065632 2.2844101
#> Trackway_03 5.120797 1.872957 NA 2.857218 1.5886871
#> Trackway_04 4.799061 1.065632 2.857218 NA 2.9457408
#> Trackway_07 3.580084 2.284410 1.588687 2.945741 NA
#> Trackway_08 3.646325 3.255445 2.122853 3.822074 0.8304850
#> Trackway_09 3.218639 2.895861 2.148764 3.481532 0.6415212
#> Trackway_13 4.466248 1.248763 1.051359 2.073897 1.0889123
#> Trackway_15 12.189111 10.642539 -1.000000 11.642355 -1.0000000
#> Trackway_16 6.478172 -1.000000 -1.000000 7.800868 4.8868854
#> Trackway_18 4.660722 2.668116 1.057879 3.470717 1.1280049
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.6463254 3.2186388 4.466248 12.189111 6.478172
#> Trackway_02 3.2554454 2.8958614 1.248763 10.642539 -1.000000
#> Trackway_03 2.1228527 2.1487640 1.051359 -1.000000 -1.000000
#> Trackway_04 3.8220737 3.4815321 2.073897 11.642355 7.800868
#> Trackway_07 0.8304850 0.6415212 1.088912 -1.000000 4.886885
#> Trackway_08 NA 0.4959895 1.855833 -1.000000 4.073736
#> Trackway_09 0.4959895 NA 1.727620 9.357244 4.476816
#> Trackway_13 1.8558326 1.7276199 NA 9.729403 5.758029
#> Trackway_15 -1.0000000 9.3572445 9.729403 NA 6.148466
#> Trackway_16 4.0737360 4.4768163 5.758029 6.148466 NA
#> Trackway_18 1.1886236 1.4726543 1.383373 8.419192 -1.000000
#> Trackway_18
#> Trackway_01 4.660722
#> Trackway_02 2.668116
#> Trackway_03 1.057879
#> Trackway_04 3.470717
#> Trackway_07 1.128005
#> Trackway_08 1.188624
#> Trackway_09 1.472654
#> Trackway_13 1.383373
#> Trackway_15 8.419192
#> Trackway_16 -1.000000
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[13]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1.183254 3.4709719 0.5173445 2.1878512
#> Trackway_02 1.1832543 NA 2.3542527 1.6514152 1.4747941
#> Trackway_03 3.4709719 2.354253 NA 4.3527229 1.9354793
#> Trackway_04 0.5173445 1.651415 4.3527229 NA 2.5622920
#> Trackway_07 2.1878512 1.474794 1.9354793 2.5622920 NA
#> Trackway_08 3.1206817 2.221332 1.5522190 3.3247015 0.7901091
#> Trackway_09 2.8781235 1.907290 1.0756256 3.3904806 0.8732637
#> Trackway_13 1.7940338 1.091621 2.1468331 2.1468331 0.4623495
#> Trackway_15 -1.0000000 -1.000000 -1.0000000 12.3897869 9.8650756
#> Trackway_16 -1.0000000 6.631179 5.1980214 7.5522100 -1.0000000
#> Trackway_18 3.3525684 2.344929 0.4595466 3.6136961 1.3785750
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.1206817 2.8781235 1.7940338 -1.000000 -1.000000
#> Trackway_02 2.2213316 1.9072901 1.0916212 -1.000000 6.631179
#> Trackway_03 1.5522190 1.0756256 2.1468331 -1.000000 5.198021
#> Trackway_04 3.3247015 3.3904806 2.1468331 12.389787 7.552210
#> Trackway_07 0.7901091 0.8732637 0.4623495 9.865076 -1.000000
#> Trackway_08 NA 0.7147312 2.0438396 -1.000000 4.419587
#> Trackway_09 0.7147312 NA 1.2509210 9.205722 -1.000000
#> Trackway_13 2.0438396 1.2509210 NA 10.252428 -1.000000
#> Trackway_15 -1.0000000 9.2057225 10.2524282 NA -1.000000
#> Trackway_16 4.4195868 -1.0000000 -1.0000000 -1.000000 NA
#> Trackway_18 1.0954723 0.5066971 1.6238866 8.875005 4.895308
#> Trackway_18
#> Trackway_01 3.3525684
#> Trackway_02 2.3449286
#> Trackway_03 0.4595466
#> Trackway_04 3.6136961
#> Trackway_07 1.3785750
#> Trackway_08 1.0954723
#> Trackway_09 0.5066971
#> Trackway_13 1.6238866
#> Trackway_15 8.8750050
#> Trackway_16 4.8953076
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[14]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1.818844 4.3703918 2.249651 3.0817428
#> Trackway_02 1.818844 NA 2.8620676 1.128277 1.8670197
#> Trackway_03 4.370392 2.862068 NA 4.129482 1.3258370
#> Trackway_04 2.249651 1.128277 4.1294823 NA 2.9549922
#> Trackway_07 3.081743 1.867020 1.3258370 2.954992 NA
#> Trackway_08 3.584607 2.681161 1.8003070 3.589584 0.8841593
#> Trackway_09 3.469232 1.889547 1.2196087 3.078356 0.1901228
#> Trackway_13 3.008499 1.336139 1.5809205 2.050445 0.9039728
#> Trackway_15 11.902807 10.982310 8.3790071 -1.000000 -1.0000000
#> Trackway_16 6.960577 6.528559 -1.0000000 7.634990 4.9879399
#> Trackway_18 4.574199 2.885091 0.2619363 3.701737 1.3415836
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.5846067 3.4692319 3.0084986 11.902807 6.960577
#> Trackway_02 2.6811608 1.8895466 1.3361386 10.982310 6.528559
#> Trackway_03 1.8003070 1.2196087 1.5809205 8.379007 -1.000000
#> Trackway_04 3.5895836 3.0783557 2.0504447 -1.000000 7.634990
#> Trackway_07 0.8841593 0.1901228 0.9039728 -1.000000 4.987940
#> Trackway_08 NA 0.8164030 1.8476392 -1.000000 4.105024
#> Trackway_09 0.8164030 NA 0.9673582 9.095950 -1.000000
#> Trackway_13 1.8476392 0.9673582 NA -1.000000 5.876421
#> Trackway_15 -1.0000000 9.0959501 -1.0000000 NA 5.635420
#> Trackway_16 4.1050241 -1.0000000 5.8764212 5.635420 NA
#> Trackway_18 1.3299045 1.1272809 1.6518292 8.248032 4.680175
#> Trackway_18
#> Trackway_01 4.5741990
#> Trackway_02 2.8850906
#> Trackway_03 0.2619363
#> Trackway_04 3.7017372
#> Trackway_07 1.3415836
#> Trackway_08 1.3299045
#> Trackway_09 1.1272809
#> Trackway_13 1.6518292
#> Trackway_15 8.2480315
#> Trackway_16 4.6801749
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[15]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0.7922255 2.8043189 1.970312 2.9015703
#> Trackway_02 0.7922255 NA 2.2791480 1.778663 2.0129910
#> Trackway_03 2.8043189 2.2791480 NA 3.633000 1.0394032
#> Trackway_04 1.9703119 1.7786631 3.6330004 NA 3.2669794
#> Trackway_07 2.9015703 2.0129910 1.0394032 3.266979 NA
#> Trackway_08 3.4955883 2.7331579 1.5840297 3.583450 0.9090184
#> Trackway_09 2.0835690 1.5574463 0.6571131 3.028557 0.8964564
#> Trackway_13 1.7965123 1.2494858 1.0663022 2.690380 1.0241036
#> Trackway_15 10.8004789 10.4767319 8.2905879 11.913349 8.9080349
#> Trackway_16 -1.0000000 -1.0000000 5.3959636 -1.000000 5.3672063
#> Trackway_18 3.0772338 2.5760307 0.2969982 3.872157 1.0002862
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.4955883 2.0835690 1.796512 10.800479 -1.000000
#> Trackway_02 2.7331579 1.5574463 1.249486 10.476732 -1.000000
#> Trackway_03 1.5840297 0.6571131 1.066302 8.290588 5.395964
#> Trackway_04 3.5834498 3.0285574 2.690380 11.913349 -1.000000
#> Trackway_07 0.9090184 0.8964564 1.024104 8.908035 5.367206
#> Trackway_08 NA 1.6391418 2.089300 8.690300 4.767822
#> Trackway_09 1.6391418 NA 0.342750 -1.000000 5.925265
#> Trackway_13 2.0893001 0.3427500 NA 9.250348 6.203187
#> Trackway_15 8.6902996 -1.0000000 9.250348 NA 5.481121
#> Trackway_16 4.7678220 5.9252650 6.203187 5.481121 NA
#> Trackway_18 1.4061830 0.8607492 1.167457 -1.000000 -1.000000
#> Trackway_18
#> Trackway_01 3.0772338
#> Trackway_02 2.5760307
#> Trackway_03 0.2969982
#> Trackway_04 3.8721566
#> Trackway_07 1.0002862
#> Trackway_08 1.4061830
#> Trackway_09 0.8607492
#> Trackway_13 1.1674572
#> Trackway_15 -1.0000000
#> Trackway_16 -1.0000000
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[16]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0.6302046 3.3639066 1.290036 1.9407432
#> Trackway_02 0.6302046 NA 3.3857729 1.671508 1.5066109
#> Trackway_03 3.3639066 3.3857729 NA 3.862558 2.0873283
#> Trackway_04 1.2900365 1.6715082 3.8625576 NA 3.1006179
#> Trackway_07 1.9407432 1.5066109 2.0873283 3.100618 NA
#> Trackway_08 2.7261008 2.3133060 1.2915845 3.703917 1.0053207
#> Trackway_09 2.6782058 2.6397586 0.7685694 3.147169 1.9948173
#> Trackway_13 1.8292168 1.3839016 1.9100321 2.900779 0.5144957
#> Trackway_15 -1.0000000 -1.0000000 -1.0000000 12.778536 -1.0000000
#> Trackway_16 7.4207806 -1.0000000 5.6999848 8.610213 5.5101520
#> Trackway_18 3.7751858 3.4290401 0.5756697 4.887588 2.7065197
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 2.7261008 2.6782058 1.8292168 -1.000000 7.420781
#> Trackway_02 2.3133060 2.6397586 1.3839016 -1.000000 -1.000000
#> Trackway_03 1.2915845 0.7685694 1.9100321 -1.000000 5.699985
#> Trackway_04 3.7039169 3.1471695 2.9007792 12.778536 8.610213
#> Trackway_07 1.0053207 1.9948173 0.5144957 -1.000000 5.510152
#> Trackway_08 NA 1.5033615 0.9304824 9.114342 5.064267
#> Trackway_09 1.5033615 NA 1.5198364 -1.000000 6.355847
#> Trackway_13 0.9304824 1.5198364 NA 10.039978 5.824402
#> Trackway_15 9.1143417 -1.0000000 10.0399777 NA 5.517266
#> Trackway_16 5.0642673 6.3558472 5.8244023 5.517266 NA
#> Trackway_18 1.4713529 1.3473901 2.3500647 8.468489 5.316375
#> Trackway_18
#> Trackway_01 3.7751858
#> Trackway_02 3.4290401
#> Trackway_03 0.5756697
#> Trackway_04 4.8875883
#> Trackway_07 2.7065197
#> Trackway_08 1.4713529
#> Trackway_09 1.3473901
#> Trackway_13 2.3500647
#> Trackway_15 8.4684892
#> Trackway_16 5.3163754
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[17]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1.207034 3.7511673 0.8883021 3.0355644
#> Trackway_02 1.2070344 NA 2.7427619 0.8437940 2.1318079
#> Trackway_03 3.7511673 2.742762 NA 3.3124340 1.6309639
#> Trackway_04 0.8883021 0.843794 3.3124340 NA 2.9746226
#> Trackway_07 3.0355644 2.131808 1.6309639 2.9746226 NA
#> Trackway_08 3.2447859 2.220522 1.0592107 3.0514552 0.5756514
#> Trackway_09 3.3324480 2.264261 1.0397288 3.0734910 0.5983223
#> Trackway_13 2.3801616 1.198697 1.4329628 1.8797075 1.6436042
#> Trackway_15 -1.0000000 -1.000000 8.1049196 -1.0000000 8.2060837
#> Trackway_16 7.5984770 -1.000000 -1.0000000 7.7966082 4.8910477
#> Trackway_18 4.0312131 2.498332 0.6506494 3.2995627 1.0405854
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.2447859 3.3324480 2.380162 -1.000000 7.598477
#> Trackway_02 2.2205218 2.2642609 1.198697 -1.000000 -1.000000
#> Trackway_03 1.0592107 1.0397288 1.432963 8.104920 -1.000000
#> Trackway_04 3.0514552 3.0734910 1.879707 -1.000000 7.796608
#> Trackway_07 0.5756514 0.5983223 1.643604 8.206084 4.891048
#> Trackway_08 NA 0.3973825 1.417643 8.079843 5.056212
#> Trackway_09 0.3973825 NA 1.429860 -1.000000 -1.000000
#> Trackway_13 1.4176432 1.4298601 NA 9.397443 6.465430
#> Trackway_15 8.0798432 -1.0000000 9.397443 NA -1.000000
#> Trackway_16 5.0562124 -1.0000000 6.465430 -1.000000 NA
#> Trackway_18 0.5003673 0.4476241 1.757834 -1.000000 -1.000000
#> Trackway_18
#> Trackway_01 4.0312131
#> Trackway_02 2.4983320
#> Trackway_03 0.6506494
#> Trackway_04 3.2995627
#> Trackway_07 1.0405854
#> Trackway_08 0.5003673
#> Trackway_09 0.4476241
#> Trackway_13 1.7578345
#> Trackway_15 -1.0000000
#> Trackway_16 -1.0000000
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[18]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1.003411 3.6615240 0.4465734 2.4316329
#> Trackway_02 1.0034114 NA 2.7482113 1.2571426 2.0318194
#> Trackway_03 3.6615240 2.748211 NA 4.4871926 2.3868838
#> Trackway_04 0.4465734 1.257143 4.4871926 NA 2.6418070
#> Trackway_07 2.4316329 2.031819 2.3868838 2.6418070 NA
#> Trackway_08 3.6099803 2.752260 0.7724865 3.8534353 1.7036904
#> Trackway_09 2.3118994 1.605246 1.6460889 2.6237902 0.9349484
#> Trackway_13 2.0975118 1.273090 1.7959992 2.3856728 1.1580301
#> Trackway_15 -1.0000000 -1.000000 7.8962608 -1.0000000 -1.0000000
#> Trackway_16 7.7269177 -1.000000 5.6411205 7.9049884 5.3158790
#> Trackway_18 3.4225387 2.639469 0.9956686 3.6953847 1.4543191
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.6099803 2.3118994 2.0975118 -1.000000 7.726918
#> Trackway_02 2.7522600 1.6052455 1.2730903 -1.000000 -1.000000
#> Trackway_03 0.7724865 1.6460889 1.7959992 7.896261 5.641120
#> Trackway_04 3.8534353 2.6237902 2.3856728 -1.000000 7.904988
#> Trackway_07 1.7036904 0.9349484 1.1580301 -1.000000 5.315879
#> Trackway_08 NA 1.2969675 1.9476798 -1.000000 5.012119
#> Trackway_09 1.2969675 NA 0.3483048 -1.000000 5.824471
#> Trackway_13 1.9476798 0.3483048 NA 9.185218 6.117512
#> Trackway_15 -1.0000000 -1.0000000 9.1852181 NA -1.000000
#> Trackway_16 5.0121192 5.8244708 6.1175117 -1.000000 NA
#> Trackway_18 0.2619965 1.1943631 1.9774249 -1.000000 4.947801
#> Trackway_18
#> Trackway_01 3.4225387
#> Trackway_02 2.6394691
#> Trackway_03 0.9956686
#> Trackway_04 3.6953847
#> Trackway_07 1.4543191
#> Trackway_08 0.2619965
#> Trackway_09 1.1943631
#> Trackway_13 1.9774249
#> Trackway_15 -1.0000000
#> Trackway_16 4.9478006
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[19]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1.733270 5.3402680 4.473077 3.3743016
#> Trackway_02 1.733270 NA 3.9856208 2.740776 2.5613666
#> Trackway_03 5.340268 3.985621 NA 3.263876 2.1694934
#> Trackway_04 4.473077 2.740776 3.2638760 NA 3.5713564
#> Trackway_07 3.374302 2.561367 2.1694934 3.571356 NA
#> Trackway_08 3.466010 2.612255 2.0814821 3.456547 0.2828045
#> Trackway_09 3.237559 2.171574 2.0633516 2.811010 0.6872206
#> Trackway_13 3.673356 2.307032 1.8892074 2.075662 1.3852696
#> Trackway_15 -1.000000 11.416687 8.3248770 11.422887 8.8587812
#> Trackway_16 6.723633 -1.000000 -1.0000000 7.993194 4.6322605
#> Trackway_18 5.707666 4.700765 0.3597104 3.487244 2.4089046
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.4660102 3.2375588 3.6733562 -1.000000 6.723633
#> Trackway_02 2.6122545 2.1715745 2.3070324 11.416687 -1.000000
#> Trackway_03 2.0814821 2.0633516 1.8892074 8.324877 -1.000000
#> Trackway_04 3.4565471 2.8110097 2.0756624 11.422887 7.993194
#> Trackway_07 0.2828045 0.6872206 1.3852696 8.858781 4.632261
#> Trackway_08 NA 0.7718695 1.3273143 8.816068 -1.000000
#> Trackway_09 0.7718695 NA 0.7647401 9.401579 -1.000000
#> Trackway_13 1.3273143 0.7647401 NA 9.672167 5.921107
#> Trackway_15 8.8160676 9.4015786 9.6721672 NA 5.586889
#> Trackway_16 -1.0000000 -1.0000000 5.9211067 5.586889 NA
#> Trackway_18 2.5194187 2.3706710 2.2773773 8.025016 5.417791
#> Trackway_18
#> Trackway_01 5.7076663
#> Trackway_02 4.7007654
#> Trackway_03 0.3597104
#> Trackway_04 3.4872435
#> Trackway_07 2.4089046
#> Trackway_08 2.5194187
#> Trackway_09 2.3706710
#> Trackway_13 2.2773773
#> Trackway_15 8.0250159
#> Trackway_16 5.4177906
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[20]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1.226696 4.3779564 1.661792 3.0843949
#> Trackway_02 1.226696 NA 3.3544421 1.039523 2.2926392
#> Trackway_03 4.377956 3.354442 NA 4.122450 1.4362543
#> Trackway_04 1.661792 1.039523 4.1224504 NA 3.2371761
#> Trackway_07 3.084395 2.292639 1.4362543 3.237176 NA
#> Trackway_08 3.112078 2.600949 1.8663912 3.544102 0.5960478
#> Trackway_09 2.460086 1.859617 2.0867653 2.878812 0.8552972
#> Trackway_13 4.686398 3.512985 1.3568656 3.990474 2.3342463
#> Trackway_15 -1.000000 11.214149 -1.0000000 -1.000000 8.9425144
#> Trackway_16 -1.000000 -1.000000 5.3173201 8.180861 -1.0000000
#> Trackway_18 3.693903 3.226661 0.9815875 3.613426 0.7064317
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.1120779 2.4600859 4.686398 -1.000000 -1.000000
#> Trackway_02 2.6009489 1.8596173 3.512985 11.214149 -1.000000
#> Trackway_03 1.8663912 2.0867653 1.356866 -1.000000 5.317320
#> Trackway_04 3.5441018 2.8788122 3.990474 -1.000000 8.180861
#> Trackway_07 0.5960478 0.8552972 2.334246 8.942514 -1.000000
#> Trackway_08 NA 0.7336740 2.881014 8.696515 4.713505
#> Trackway_09 0.7336740 NA 2.931584 9.379345 5.328456
#> Trackway_13 2.8810140 2.9315844 NA -1.000000 6.641747
#> Trackway_15 8.6965152 9.3793447 -1.000000 NA 5.073699
#> Trackway_16 4.7135048 5.3284562 6.641747 5.073699 NA
#> Trackway_18 1.1636458 1.4071192 1.737563 8.639398 5.257266
#> Trackway_18
#> Trackway_01 3.6939028
#> Trackway_02 3.2266606
#> Trackway_03 0.9815875
#> Trackway_04 3.6134261
#> Trackway_07 0.7064317
#> Trackway_08 1.1636458
#> Trackway_09 1.4071192
#> Trackway_13 1.7375634
#> Trackway_15 8.6393984
#> Trackway_16 5.2572662
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[21]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1.593628 3.9783534 2.042188 2.769306
#> Trackway_02 1.593628 NA 2.7900458 1.536189 2.667490
#> Trackway_03 3.978353 2.790046 NA 3.962341 2.540941
#> Trackway_04 2.042188 1.536189 3.9623406 NA 3.980167
#> Trackway_07 2.769306 2.667490 2.5409412 3.980167 NA
#> Trackway_08 2.826311 2.375049 1.8932295 3.720424 0.606519
#> Trackway_09 2.476472 1.677759 1.5749007 3.021177 1.348000
#> Trackway_13 1.930057 1.160123 2.1273358 2.356535 1.723765
#> Trackway_15 11.780570 10.903498 8.1523639 12.114649 -1.000000
#> Trackway_16 7.221601 6.990622 -1.0000000 -1.000000 -1.000000
#> Trackway_18 4.391254 3.113566 0.4850167 4.203109 2.863191
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 2.8263115 2.4764716 1.9300567 11.780570 7.221601
#> Trackway_02 2.3750490 1.6777595 1.1601233 10.903498 6.990622
#> Trackway_03 1.8932295 1.5749007 2.1273358 8.152364 -1.000000
#> Trackway_04 3.7204243 3.0211770 2.3565350 12.114649 -1.000000
#> Trackway_07 0.6065190 1.3479995 1.7237654 -1.000000 -1.000000
#> Trackway_08 NA 0.7766205 1.3711197 8.962597 4.618488
#> Trackway_09 0.7766205 NA 0.6797057 -1.000000 5.331814
#> Trackway_13 1.3711197 0.6797057 NA -1.000000 -1.000000
#> Trackway_15 8.9625969 -1.0000000 -1.0000000 NA 5.879462
#> Trackway_16 4.6184882 5.3318144 -1.0000000 5.879462 NA
#> Trackway_18 2.2793967 2.0380174 2.6491299 -1.000000 5.240931
#> Trackway_18
#> Trackway_01 4.3912537
#> Trackway_02 3.1135665
#> Trackway_03 0.4850167
#> Trackway_04 4.2031092
#> Trackway_07 2.8631915
#> Trackway_08 2.2793967
#> Trackway_09 2.0380174
#> Trackway_13 2.6491299
#> Trackway_15 -1.0000000
#> Trackway_16 5.2409309
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[22]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0.5436624 4.2457610 2.665396 2.5123956
#> Trackway_02 0.5436624 NA 3.1387638 2.661752 2.0148518
#> Trackway_03 4.2457610 3.1387638 NA 3.948760 2.1411054
#> Trackway_04 2.6653960 2.6617516 3.9487602 NA 4.6543035
#> Trackway_07 2.5123956 2.0148518 2.1411054 4.654304 NA
#> Trackway_08 3.2343757 2.7036865 1.5462998 5.071296 0.9283080
#> Trackway_09 2.9503992 2.4667622 0.9683814 2.990527 2.2871037
#> Trackway_13 1.8745396 1.3064604 2.0003371 3.428360 0.8987772
#> Trackway_15 12.3570015 11.8211869 9.0965836 -1.000000 -1.0000000
#> Trackway_16 -1.0000000 -1.0000000 -1.0000000 -1.000000 -1.0000000
#> Trackway_18 3.4318432 2.8930429 0.9137303 4.028958 1.6993850
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.234376 2.9503992 1.8745396 12.357002 -1.000000
#> Trackway_02 2.703686 2.4667622 1.3064604 11.821187 -1.000000
#> Trackway_03 1.546300 0.9683814 2.0003371 9.096584 -1.000000
#> Trackway_04 5.071296 2.9905274 3.4283602 -1.000000 -1.000000
#> Trackway_07 0.928308 2.2871037 0.8987772 -1.000000 -1.000000
#> Trackway_08 NA 1.9356461 1.7851909 -1.000000 4.598251
#> Trackway_09 1.935646 NA 1.6321609 -1.000000 -1.000000
#> Trackway_13 1.785191 1.6321609 NA 10.516585 5.900721
#> Trackway_15 -1.000000 -1.0000000 10.5165849 NA 6.127098
#> Trackway_16 4.598251 -1.0000000 5.9007211 6.127098 NA
#> Trackway_18 1.088356 1.0871877 1.6703593 9.120302 5.277575
#> Trackway_18
#> Trackway_01 3.4318432
#> Trackway_02 2.8930429
#> Trackway_03 0.9137303
#> Trackway_04 4.0289576
#> Trackway_07 1.6993850
#> Trackway_08 1.0883564
#> Trackway_09 1.0871877
#> Trackway_13 1.6703593
#> Trackway_15 9.1203016
#> Trackway_16 5.2775751
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[23]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0.6917645 4.1362332 1.572295 2.5274523
#> Trackway_02 0.6917645 NA 3.5365982 2.024928 2.0085551
#> Trackway_03 4.1362332 3.5365982 NA 3.453492 1.6124399
#> Trackway_04 1.5722949 2.0249276 3.4534919 NA 2.6193065
#> Trackway_07 2.5274523 2.0085551 1.6124399 2.619307 NA
#> Trackway_08 2.9867669 2.4512153 1.7457278 3.384053 0.7845213
#> Trackway_09 3.0062568 2.7876207 0.8397008 2.730490 0.8972000
#> Trackway_13 1.9016683 1.6364305 1.9335555 1.925415 0.6940412
#> Trackway_15 11.3760889 10.8608545 -1.0000000 -1.000000 -1.0000000
#> Trackway_16 6.5800728 5.9296357 4.7201063 7.250828 4.6629464
#> Trackway_18 4.0970135 3.5895251 0.1962974 3.509351 1.9277249
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 2.9867669 3.0062568 1.9016683 11.376089 6.580073
#> Trackway_02 2.4512153 2.7876207 1.6364305 10.860854 5.929636
#> Trackway_03 1.7457278 0.8397008 1.9335555 -1.000000 4.720106
#> Trackway_04 3.3840528 2.7304904 1.9254154 -1.000000 7.250828
#> Trackway_07 0.7845213 0.8972000 0.6940412 -1.000000 4.662946
#> Trackway_08 NA 1.3357380 1.4647492 8.409850 3.875306
#> Trackway_09 1.3357380 NA 1.1075171 -1.000000 -1.000000
#> Trackway_13 1.4647492 1.1075171 NA 9.586142 5.339628
#> Trackway_15 8.4098498 -1.0000000 9.5861416 NA -1.000000
#> Trackway_16 3.8753058 -1.0000000 5.3396285 -1.000000 NA
#> Trackway_18 1.7737581 1.0047150 1.9965834 -1.000000 4.698452
#> Trackway_18
#> Trackway_01 4.0970135
#> Trackway_02 3.5895251
#> Trackway_03 0.1962974
#> Trackway_04 3.5093513
#> Trackway_07 1.9277249
#> Trackway_08 1.7737581
#> Trackway_09 1.0047150
#> Trackway_13 1.9965834
#> Trackway_15 -1.0000000
#> Trackway_16 4.6984519
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[24]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0.7514253 3.3807136 0.4758597 2.693814
#> Trackway_02 0.7514253 NA 2.7990619 1.6681769 1.949169
#> Trackway_03 3.3807136 2.7990619 NA 3.6764356 1.637205
#> Trackway_04 0.4758597 1.6681769 3.6764356 NA 3.215778
#> Trackway_07 2.6938141 1.9491688 1.6372047 3.2157783 NA
#> Trackway_08 3.1770183 2.4263605 2.2536857 3.5860196 0.659809
#> Trackway_09 3.1581715 2.6356411 0.4282233 3.4402908 1.905804
#> Trackway_13 2.1491850 1.5096568 3.2531890 2.5063108 1.497342
#> Trackway_15 11.5743959 -1.0000000 8.3749443 11.9248507 -1.000000
#> Trackway_16 -1.0000000 -1.0000000 5.2359336 7.6996444 4.709340
#> Trackway_18 3.0420051 2.1258962 1.1118592 3.1926330 0.525354
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.177018 3.1581715 2.149185 11.574396 -1.000000
#> Trackway_02 2.426361 2.6356411 1.509657 -1.000000 -1.000000
#> Trackway_03 2.253686 0.4282233 3.253189 8.374944 5.235934
#> Trackway_04 3.586020 3.4402908 2.506311 11.924851 7.699644
#> Trackway_07 0.659809 1.9058044 1.497342 -1.000000 4.709340
#> Trackway_08 NA 2.4200736 1.532751 8.693849 4.139729
#> Trackway_09 2.420074 NA 3.075182 -1.000000 5.623595
#> Trackway_13 1.532751 3.0751822 NA 10.217723 5.378929
#> Trackway_15 8.693849 -1.0000000 10.217723 NA 5.822879
#> Trackway_16 4.139729 5.6235954 5.378929 5.822879 NA
#> Trackway_18 1.064581 1.2986619 1.976850 8.744069 4.821973
#> Trackway_18
#> Trackway_01 3.042005
#> Trackway_02 2.125896
#> Trackway_03 1.111859
#> Trackway_04 3.192633
#> Trackway_07 0.525354
#> Trackway_08 1.064581
#> Trackway_09 1.298662
#> Trackway_13 1.976850
#> Trackway_15 8.744069
#> Trackway_16 4.821973
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[25]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 2.976841 4.5481715 0.8206778 2.462719
#> Trackway_02 2.9768405 NA 2.6928258 2.8130189 2.677121
#> Trackway_03 4.5481715 2.692826 NA 4.6370989 2.431821
#> Trackway_04 0.8206778 2.813019 4.6370989 NA 2.972286
#> Trackway_07 2.4627194 2.677121 2.4318211 2.9722857 NA
#> Trackway_08 3.4073382 2.566091 1.2225863 4.0922256 1.082321
#> Trackway_09 5.1397669 2.896911 0.9991930 5.2263055 3.210515
#> Trackway_13 2.8930418 1.717148 1.9873570 3.0566131 1.344788
#> Trackway_15 -1.0000000 11.363738 -1.0000000 12.9399387 -1.000000
#> Trackway_16 6.1935432 6.385095 -1.0000000 7.0685012 4.034040
#> Trackway_18 3.6738065 2.521641 0.7956799 3.9614963 1.490354
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.4073382 5.139767 2.893042 -1.000000 6.193543
#> Trackway_02 2.5660909 2.896911 1.717148 11.363738 6.385095
#> Trackway_03 1.2225863 0.999193 1.987357 -1.000000 -1.000000
#> Trackway_04 4.0922256 5.226305 3.056613 12.939939 7.068501
#> Trackway_07 1.0823213 3.210515 1.344788 -1.000000 4.034040
#> Trackway_08 NA 2.300288 1.068273 9.199294 3.823776
#> Trackway_09 2.3002884 NA 2.301949 -1.000000 5.033714
#> Trackway_13 1.0682735 2.301949 NA 10.122751 4.881148
#> Trackway_15 9.1992938 -1.000000 10.122751 NA -1.000000
#> Trackway_16 3.8237756 5.033714 4.881148 -1.000000 NA
#> Trackway_18 0.9929833 1.755393 1.102340 -1.000000 4.076945
#> Trackway_18
#> Trackway_01 3.6738065
#> Trackway_02 2.5216408
#> Trackway_03 0.7956799
#> Trackway_04 3.9614963
#> Trackway_07 1.4903542
#> Trackway_08 0.9929833
#> Trackway_09 1.7553932
#> Trackway_13 1.1023402
#> Trackway_15 -1.0000000
#> Trackway_16 4.0769451
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[26]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1.789092 3.1445625 0.5301414 3.1787100
#> Trackway_02 1.7890920 NA 2.8409464 1.9326733 1.8250302
#> Trackway_03 3.1445625 2.840946 NA 3.4969118 2.0163693
#> Trackway_04 0.5301414 1.932673 3.4969118 NA 3.4560571
#> Trackway_07 3.1787100 1.825030 2.0163693 3.4560571 NA
#> Trackway_08 3.2061881 2.401648 1.0894171 3.5524124 0.9771398
#> Trackway_09 3.3013511 1.889136 2.2428003 3.5856272 0.1588160
#> Trackway_13 2.0897301 2.072021 0.9599686 2.6259904 1.9185780
#> Trackway_15 -1.0000000 -1.000000 8.1667819 -1.0000000 9.1146711
#> Trackway_16 7.6686690 6.445068 -1.0000000 8.0174888 4.6276236
#> Trackway_18 3.0283769 2.605278 0.3986618 3.4689494 1.6262885
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.2061881 3.301351 2.0897301 -1.000000 7.668669
#> Trackway_02 2.4016477 1.889136 2.0720210 -1.000000 6.445068
#> Trackway_03 1.0894171 2.242800 0.9599686 8.166782 -1.000000
#> Trackway_04 3.5524124 3.585627 2.6259904 -1.000000 8.017489
#> Trackway_07 0.9771398 0.158816 1.9185780 9.114671 4.627624
#> Trackway_08 NA 1.103255 1.3514253 8.424296 4.518675
#> Trackway_09 1.1032551 NA 2.0773564 9.135372 4.555933
#> Trackway_13 1.3514253 2.077356 NA -1.000000 -1.000000
#> Trackway_15 8.4242962 9.135372 -1.0000000 NA -1.000000
#> Trackway_16 4.5186749 4.555933 -1.0000000 -1.000000 NA
#> Trackway_18 0.7908258 1.766365 0.9798775 8.254030 4.859570
#> Trackway_18
#> Trackway_01 3.0283769
#> Trackway_02 2.6052782
#> Trackway_03 0.3986618
#> Trackway_04 3.4689494
#> Trackway_07 1.6262885
#> Trackway_08 0.7908258
#> Trackway_09 1.7663646
#> Trackway_13 0.9798775
#> Trackway_15 8.2540298
#> Trackway_16 4.8595701
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[27]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0.3741635 3.3642960 1.205026 2.686918
#> Trackway_02 0.3741635 NA 3.4798208 1.274769 2.346205
#> Trackway_03 3.3642960 3.4798208 NA 4.017625 1.418665
#> Trackway_04 1.2050257 1.2747689 4.0176248 NA 3.581122
#> Trackway_07 2.6869177 2.3462050 1.4186649 3.581122 NA
#> Trackway_08 2.9861199 2.4454992 1.5182033 3.699509 0.180167
#> Trackway_09 3.0276743 2.7231554 0.4708169 3.615487 1.507720
#> Trackway_13 1.8268298 1.4209429 1.5749684 2.711889 2.132932
#> Trackway_15 -1.0000000 -1.0000000 -1.0000000 12.375900 8.802855
#> Trackway_16 -1.0000000 -1.0000000 -1.0000000 7.935247 -1.000000
#> Trackway_18 3.8209998 3.4468448 0.5319000 4.517776 1.626247
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 2.986120 3.0276743 1.826830 -1.000000 -1.000000
#> Trackway_02 2.445499 2.7231554 1.420943 -1.000000 -1.000000
#> Trackway_03 1.518203 0.4708169 1.574968 -1.000000 -1.000000
#> Trackway_04 3.699509 3.6154874 2.711889 12.375900 7.935247
#> Trackway_07 0.180167 1.5077202 2.132932 8.802855 -1.000000
#> Trackway_08 NA 1.7347465 1.989573 8.696025 4.451131
#> Trackway_09 1.734747 NA 1.310174 -1.000000 5.686303
#> Trackway_13 1.989573 1.3101744 NA -1.000000 5.797016
#> Trackway_15 8.696025 -1.0000000 -1.000000 NA -1.000000
#> Trackway_16 4.451131 5.6863035 5.797016 -1.000000 NA
#> Trackway_18 1.704936 1.0000372 2.026914 8.091331 4.911868
#> Trackway_18
#> Trackway_01 3.821000
#> Trackway_02 3.446845
#> Trackway_03 0.531900
#> Trackway_04 4.517776
#> Trackway_07 1.626247
#> Trackway_08 1.704936
#> Trackway_09 1.000037
#> Trackway_13 2.026914
#> Trackway_15 8.091331
#> Trackway_16 4.911868
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[28]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1.197898 4.2350848 1.645895 2.1096101
#> Trackway_02 1.197898 NA 2.9246233 1.166339 1.8097277
#> Trackway_03 4.235085 2.924623 NA 3.707680 2.5413146
#> Trackway_04 1.645895 1.166339 3.7076800 NA 2.9760549
#> Trackway_07 2.109610 1.809728 2.5413146 2.976055 NA
#> Trackway_08 2.632645 2.484839 2.5888144 3.651125 0.8860441
#> Trackway_09 2.681659 1.905039 1.2315682 2.905802 1.3261580
#> Trackway_13 2.171357 1.327369 1.6678593 2.323528 1.2078706
#> Trackway_15 11.637882 -1.000000 -1.0000000 12.011860 9.6056074
#> Trackway_16 -1.000000 7.467046 -1.0000000 8.605530 -1.0000000
#> Trackway_18 3.649901 2.753097 0.9418437 3.568735 2.2140814
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 2.6326450 2.6816594 2.1713569 11.637882 -1.000000
#> Trackway_02 2.4848394 1.9050392 1.3273689 -1.000000 7.467046
#> Trackway_03 2.5888144 1.2315682 1.6678593 -1.000000 -1.000000
#> Trackway_04 3.6511250 2.9058018 2.3235281 12.011860 8.605530
#> Trackway_07 0.8860441 1.3261580 1.2078706 9.605607 -1.000000
#> Trackway_08 NA 1.5856975 1.7620581 9.135953 5.093973
#> Trackway_09 1.5856975 NA 0.5884113 9.138582 5.805836
#> Trackway_13 1.7620581 0.5884113 NA 9.726489 6.338301
#> Trackway_15 9.1359533 9.1385819 9.7264894 NA 4.968159
#> Trackway_16 5.0939727 5.8058364 6.3383006 4.968159 NA
#> Trackway_18 2.4161739 1.0296661 1.4787833 8.476477 5.651317
#> Trackway_18
#> Trackway_01 3.6499011
#> Trackway_02 2.7530972
#> Trackway_03 0.9418437
#> Trackway_04 3.5687352
#> Trackway_07 2.2140814
#> Trackway_08 2.4161739
#> Trackway_09 1.0296661
#> Trackway_13 1.4787833
#> Trackway_15 8.4764767
#> Trackway_16 5.6513165
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[29]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1.345458 3.4740224 2.359465 2.6235978
#> Trackway_02 1.345458 NA 2.3786526 1.314648 2.1954434
#> Trackway_03 3.474022 2.378653 NA 3.057319 1.6530020
#> Trackway_04 2.359465 1.314648 3.0573189 NA 3.3510976
#> Trackway_07 2.623598 2.195443 1.6530020 3.351098 NA
#> Trackway_08 2.945618 2.063751 1.1002997 3.157376 0.5532652
#> Trackway_09 2.293014 1.906077 1.8558565 3.171724 0.4470277
#> Trackway_13 2.490900 1.387050 0.9985219 2.468401 1.2626327
#> Trackway_15 -1.000000 -1.000000 8.4812010 -1.000000 9.1515255
#> Trackway_16 -1.000000 6.846649 -1.0000000 7.993970 -1.0000000
#> Trackway_18 3.304274 2.318939 0.4523066 3.193123 1.2360781
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 2.9456180 2.2930139 2.4909004 -1.000000 -1.000000
#> Trackway_02 2.0637508 1.9060767 1.3870502 -1.000000 6.846649
#> Trackway_03 1.1002997 1.8558565 0.9985219 8.481201 -1.000000
#> Trackway_04 3.1573762 3.1717243 2.4684006 -1.000000 7.993970
#> Trackway_07 0.5532652 0.4470277 1.2626327 9.151525 -1.000000
#> Trackway_08 NA 0.7874777 0.9042507 8.880459 4.836770
#> Trackway_09 0.7874777 NA 1.3361576 -1.000000 4.992790
#> Trackway_13 0.9042507 1.3361576 NA -1.000000 5.708795
#> Trackway_15 8.8804586 -1.0000000 -1.0000000 NA 5.968819
#> Trackway_16 4.8367695 4.9927902 5.7087954 5.968819 NA
#> Trackway_18 0.6865014 1.4691081 0.9859856 8.488200 -1.000000
#> Trackway_18
#> Trackway_01 3.3042743
#> Trackway_02 2.3189391
#> Trackway_03 0.4523066
#> Trackway_04 3.1931229
#> Trackway_07 1.2360781
#> Trackway_08 0.6865014
#> Trackway_09 1.4691081
#> Trackway_13 0.9859856
#> Trackway_15 8.4881999
#> Trackway_16 -1.0000000
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[30]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1.8258441 3.9054634 2.997139 3.1042084
#> Trackway_02 1.825844 NA 2.4549059 1.950351 2.2366573
#> Trackway_03 3.905463 2.4549059 NA 3.843296 1.9183155
#> Trackway_04 2.997139 1.9503508 3.8432959 NA 4.3289355
#> Trackway_07 3.104208 2.2366573 1.9183155 4.328936 NA
#> Trackway_08 3.474503 2.2860842 0.8865455 3.978053 1.1861497
#> Trackway_09 3.714567 2.0517392 0.7043003 3.248402 2.2601437
#> Trackway_13 2.362119 0.8114734 1.8271155 2.349461 2.0499144
#> Trackway_15 11.760242 10.5858054 8.1719434 11.897109 9.0351998
#> Trackway_16 7.604220 7.1269904 -1.0000000 8.955074 -1.0000000
#> Trackway_18 2.933827 2.1470807 1.6034004 4.035061 0.4506193
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.4745026 3.7145670 2.3621193 11.760242 7.604220
#> Trackway_02 2.2860842 2.0517392 0.8114734 10.585805 7.126990
#> Trackway_03 0.8865455 0.7043003 1.8271155 8.171943 -1.000000
#> Trackway_04 3.9780534 3.2484021 2.3494614 11.897109 8.955074
#> Trackway_07 1.1861497 2.2601437 2.0499144 9.035200 -1.000000
#> Trackway_08 NA 1.2542919 1.6677451 -1.000000 4.992341
#> Trackway_09 1.2542919 NA 1.5875351 8.715272 6.031490
#> Trackway_13 1.6677451 1.5875351 NA 9.909339 6.609931
#> Trackway_15 -1.0000000 8.7152718 9.9093395 NA 5.508464
#> Trackway_16 4.9923411 6.0314901 6.6099309 5.508464 NA
#> Trackway_18 0.7937924 1.8876413 1.7036530 8.826810 4.983924
#> Trackway_18
#> Trackway_01 2.9338270
#> Trackway_02 2.1470807
#> Trackway_03 1.6034004
#> Trackway_04 4.0350606
#> Trackway_07 0.4506193
#> Trackway_08 0.7937924
#> Trackway_09 1.8876413
#> Trackway_13 1.7036530
#> Trackway_15 8.8268100
#> Trackway_16 4.9839239
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[31]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1.0999863 2.3942868 3.058056 2.3078977
#> Trackway_02 1.099986 NA 2.2422742 2.054374 1.5112897
#> Trackway_03 2.394287 2.2422742 NA 3.824079 1.4383454
#> Trackway_04 3.058056 2.0543740 3.8240792 NA 2.4959997
#> Trackway_07 2.307898 1.5112897 1.4383454 2.496000 NA
#> Trackway_08 2.613456 2.2370226 0.3147971 3.720999 1.2924005
#> Trackway_09 3.262245 2.2430875 2.0673612 2.565396 0.8856093
#> Trackway_13 1.180981 0.7933693 1.4749611 2.679869 1.1432253
#> Trackway_15 10.411579 10.5003362 8.2593910 -1.000000 -1.0000000
#> Trackway_16 -1.000000 6.8993365 -1.0000000 -1.000000 5.4260504
#> Trackway_18 2.489499 2.0632916 0.5942413 3.387302 0.9591989
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 2.6134555 3.2622446 1.1809806 10.411579 -1.000000
#> Trackway_02 2.2370226 2.2430875 0.7933693 10.500336 6.899337
#> Trackway_03 0.3147971 2.0673612 1.4749611 8.259391 -1.000000
#> Trackway_04 3.7209995 2.5653961 2.6798694 -1.000000 -1.000000
#> Trackway_07 1.2924005 0.8856093 1.1432253 -1.000000 5.426050
#> Trackway_08 NA 1.8714374 1.4916901 -1.000000 4.906124
#> Trackway_09 1.8714374 NA 2.0169865 9.454414 5.004509
#> Trackway_13 1.4916901 2.0169865 NA -1.000000 6.288018
#> Trackway_15 -1.0000000 9.4544144 -1.0000000 NA 5.654602
#> Trackway_16 4.9061244 5.0045092 6.2880183 5.654602 NA
#> Trackway_18 0.4002462 1.4739040 1.3837575 -1.000000 4.908548
#> Trackway_18
#> Trackway_01 2.4894994
#> Trackway_02 2.0632916
#> Trackway_03 0.5942413
#> Trackway_04 3.3873021
#> Trackway_07 0.9591989
#> Trackway_08 0.4002462
#> Trackway_09 1.4739040
#> Trackway_13 1.3837575
#> Trackway_15 -1.0000000
#> Trackway_16 4.9085478
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[32]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0.7808674 3.697397 2.801089 2.7000345
#> Trackway_02 0.7808674 NA 2.989950 2.993168 2.0889325
#> Trackway_03 3.6973969 2.9899503 NA 5.371769 1.9605814
#> Trackway_04 2.8010895 2.9931679 5.371769 NA 3.6192171
#> Trackway_07 2.7000345 2.0889325 1.960581 3.619217 NA
#> Trackway_08 3.2778986 2.6771135 2.041413 3.707806 0.3626422
#> Trackway_09 2.4325424 1.9151062 2.477057 3.018872 0.5442435
#> Trackway_13 1.7614708 1.1417368 2.226666 3.470559 1.1732042
#> Trackway_15 11.3303864 10.6516673 7.989725 -1.000000 -1.0000000
#> Trackway_16 7.7878307 7.2292103 5.551142 -1.000000 -1.0000000
#> Trackway_18 3.6688612 2.9590669 0.384322 5.164191 1.6726687
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.2778986 2.4325424 1.761471 11.330386 7.787831
#> Trackway_02 2.6771135 1.9151062 1.141737 10.651667 7.229210
#> Trackway_03 2.0414133 2.4770566 2.226666 7.989725 5.551142
#> Trackway_04 3.7078055 3.0188718 3.470559 -1.000000 -1.000000
#> Trackway_07 0.3626422 0.5442435 1.173204 -1.000000 -1.000000
#> Trackway_08 NA 0.7186097 1.518781 -1.000000 4.789432
#> Trackway_09 0.7186097 NA 1.219998 9.093396 -1.000000
#> Trackway_13 1.5187808 1.2199984 NA 9.588753 -1.000000
#> Trackway_15 -1.0000000 9.0933955 9.588753 NA 4.807110
#> Trackway_16 4.7894325 -1.0000000 -1.000000 4.807110 NA
#> Trackway_18 1.7096586 2.2068713 1.973164 7.845441 -1.000000
#> Trackway_18
#> Trackway_01 3.668861
#> Trackway_02 2.959067
#> Trackway_03 0.384322
#> Trackway_04 5.164191
#> Trackway_07 1.672669
#> Trackway_08 1.709659
#> Trackway_09 2.206871
#> Trackway_13 1.973164
#> Trackway_15 7.845441
#> Trackway_16 -1.000000
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[33]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 3.6765413 4.545002 3.8925300 3.0319000
#> Trackway_02 3.676541 NA 2.511796 0.5141714 2.2835282
#> Trackway_03 4.545002 2.5117964 NA 3.1615645 1.6572541
#> Trackway_04 3.892530 0.5141714 3.161565 NA 2.9424314
#> Trackway_07 3.031900 2.2835282 1.657254 2.9424314 NA
#> Trackway_08 3.054628 3.5120038 2.569055 4.0172819 1.2354863
#> Trackway_09 3.214673 2.1970084 1.343894 2.7043554 0.4238881
#> Trackway_13 3.585281 1.3505950 1.283606 1.8621824 1.1595059
#> Trackway_15 12.369786 -1.0000000 8.891631 11.8525001 9.8719867
#> Trackway_16 6.488018 7.0137271 4.885802 7.5275098 4.8235364
#> Trackway_18 4.173203 2.5534467 1.043048 3.0674425 0.7827015
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.054628 3.2146725 3.5852807 12.369786 6.488018
#> Trackway_02 3.512004 2.1970084 1.3505950 -1.000000 7.013727
#> Trackway_03 2.569055 1.3438937 1.2836061 8.891631 4.885802
#> Trackway_04 4.017282 2.7043554 1.8621824 11.852500 7.527510
#> Trackway_07 1.235486 0.4238881 1.1595059 9.871987 4.823536
#> Trackway_08 NA 1.4042870 2.3620928 9.325699 3.794752
#> Trackway_09 1.404287 NA 0.9593433 9.714532 -1.000000
#> Trackway_13 2.362093 0.9593433 NA 10.147155 5.683960
#> Trackway_15 9.325699 9.7145322 10.1471546 NA 6.391207
#> Trackway_16 3.794752 -1.0000000 5.6839597 6.391207 NA
#> Trackway_18 1.445269 0.6691874 1.2141935 9.174315 4.469805
#> Trackway_18
#> Trackway_01 4.1732033
#> Trackway_02 2.5534467
#> Trackway_03 1.0430476
#> Trackway_04 3.0674425
#> Trackway_07 0.7827015
#> Trackway_08 1.4452690
#> Trackway_09 0.6691874
#> Trackway_13 1.2141935
#> Trackway_15 9.1743149
#> Trackway_16 4.4698053
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[34]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0.7182332 2.5664826 1.102942 2.4508154
#> Trackway_02 0.7182332 NA 2.6127060 1.662585 2.0245230
#> Trackway_03 2.5664826 2.6127060 NA 3.444676 1.6967663
#> Trackway_04 1.1029418 1.6625846 3.4446765 NA 3.4267024
#> Trackway_07 2.4508154 2.0245230 1.6967663 3.426702 NA
#> Trackway_08 2.4668398 2.1920292 1.0043598 3.331205 0.8982169
#> Trackway_09 2.3124003 1.5964641 1.6414271 3.003447 0.4491618
#> Trackway_13 1.4756557 2.0072677 1.5685861 1.913805 2.3640071
#> Trackway_15 10.4066514 -1.0000000 7.8524905 10.958755 -1.0000000
#> Trackway_16 6.8328629 6.4674712 4.7380893 -1.000000 4.4437293
#> Trackway_18 2.9589497 3.1155257 0.7264319 3.505337 2.3827587
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 2.4668398 2.3124003 1.475656 10.406651 6.832863
#> Trackway_02 2.1920292 1.5964641 2.007268 -1.000000 6.467471
#> Trackway_03 1.0043598 1.6414271 1.568586 7.852491 4.738089
#> Trackway_04 3.3312051 3.0034470 1.913805 10.958755 -1.000000
#> Trackway_07 0.8982169 0.4491618 2.364007 -1.000000 4.443729
#> Trackway_08 NA 0.7775722 1.955419 8.259620 4.404954
#> Trackway_09 0.7775722 NA 2.174607 9.007339 -1.000000
#> Trackway_13 1.9554192 2.1746072 NA 9.130385 6.187814
#> Trackway_15 8.2596195 9.0073386 9.130385 NA 5.679109
#> Trackway_16 4.4049543 -1.0000000 6.187814 5.679109 NA
#> Trackway_18 1.7252718 2.3590527 2.014632 7.517032 -1.000000
#> Trackway_18
#> Trackway_01 2.9589497
#> Trackway_02 3.1155257
#> Trackway_03 0.7264319
#> Trackway_04 3.5053368
#> Trackway_07 2.3827587
#> Trackway_08 1.7252718
#> Trackway_09 2.3590527
#> Trackway_13 2.0146325
#> Trackway_15 7.5170320
#> Trackway_16 -1.0000000
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[35]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 2.822335 4.2907355 1.392291 3.3801281
#> Trackway_02 2.822335 NA 2.3513015 2.229352 1.9186432
#> Trackway_03 4.290735 2.351301 NA 4.237575 1.1103652
#> Trackway_04 1.392291 2.229352 4.2375747 NA 3.5360531
#> Trackway_07 3.380128 1.918643 1.1103652 3.536053 NA
#> Trackway_08 3.514828 2.314054 1.2805806 3.713623 0.6774572
#> Trackway_09 3.166831 1.371430 1.1278981 3.126961 0.5629346
#> Trackway_13 3.009252 1.349685 1.2709150 3.012157 0.6811161
#> Trackway_15 -1.000000 -1.000000 8.4748289 12.470904 8.9629314
#> Trackway_16 6.569721 -1.000000 4.9129199 7.501399 4.6948273
#> Trackway_18 4.183240 2.187423 0.9675582 4.183240 0.4798810
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.5148285 3.1668306 3.0092522 -1.000000 6.569721
#> Trackway_02 2.3140544 1.3714301 1.3496846 -1.000000 -1.000000
#> Trackway_03 1.2805806 1.1278981 1.2709150 8.474829 4.912920
#> Trackway_04 3.7136231 3.1269607 3.0121573 12.470904 7.501399
#> Trackway_07 0.6774572 0.5629346 0.6811161 8.962931 4.694827
#> Trackway_08 NA 1.0092739 0.9754472 8.758179 -1.000000
#> Trackway_09 1.0092739 NA 0.1967001 -1.000000 -1.000000
#> Trackway_13 0.9754472 0.1967001 NA -1.000000 -1.000000
#> Trackway_15 8.7581787 -1.0000000 -1.0000000 NA -1.000000
#> Trackway_16 -1.0000000 -1.0000000 -1.0000000 -1.000000 NA
#> Trackway_18 0.7485479 0.8588234 0.9996603 8.588458 4.621782
#> Trackway_18
#> Trackway_01 4.1832403
#> Trackway_02 2.1874233
#> Trackway_03 0.9675582
#> Trackway_04 4.1832403
#> Trackway_07 0.4798810
#> Trackway_08 0.7485479
#> Trackway_09 0.8588234
#> Trackway_13 0.9996603
#> Trackway_15 8.5884584
#> Trackway_16 4.6217825
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[36]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 2.2441160 3.4042055 0.4375853 2.8594802
#> Trackway_02 2.2441160 NA 1.8023079 2.3190118 2.2965836
#> Trackway_03 3.4042055 1.8023079 NA 3.5864269 1.3011090
#> Trackway_04 0.4375853 2.3190118 3.5864269 NA 3.2353845
#> Trackway_07 2.8594802 2.2965836 1.3011090 3.2353845 NA
#> Trackway_08 3.4077892 2.4391722 0.9515697 3.5340364 0.5374293
#> Trackway_09 4.1752511 1.9629393 1.1387720 4.1978919 2.4341095
#> Trackway_13 2.5284324 0.8277668 1.0171196 2.6776736 1.5164259
#> Trackway_15 11.6101428 -1.0000000 -1.0000000 -1.0000000 -1.0000000
#> Trackway_16 6.6613790 6.0776718 4.4788849 6.9195038 3.8992468
#> Trackway_18 4.2006637 2.5145480 0.7987338 4.6777875 1.8390445
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.4077892 4.175251 2.5284324 11.610143 6.661379
#> Trackway_02 2.4391722 1.962939 0.8277668 -1.000000 6.077672
#> Trackway_03 0.9515697 1.138772 1.0171196 -1.000000 4.478885
#> Trackway_04 3.5340364 4.197892 2.6776736 -1.000000 6.919504
#> Trackway_07 0.5374293 2.434110 1.5164259 -1.000000 3.899247
#> Trackway_08 NA 2.076517 1.5287592 8.313827 3.796681
#> Trackway_09 2.0765174 NA 1.5453217 -1.000000 -1.000000
#> Trackway_13 1.5287592 1.545322 NA -1.000000 5.263100
#> Trackway_15 8.3138269 -1.000000 -1.0000000 NA -1.000000
#> Trackway_16 3.7966808 -1.000000 5.2631000 -1.000000 NA
#> Trackway_18 1.4586660 1.113179 1.7856647 7.751804 -1.000000
#> Trackway_18
#> Trackway_01 4.2006637
#> Trackway_02 2.5145480
#> Trackway_03 0.7987338
#> Trackway_04 4.6777875
#> Trackway_07 1.8390445
#> Trackway_08 1.4586660
#> Trackway_09 1.1131792
#> Trackway_13 1.7856647
#> Trackway_15 7.7518044
#> Trackway_16 -1.0000000
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[37]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0.9901942 3.0226495 0.4783721 3.1533083
#> Trackway_02 0.9901942 NA 2.0482129 1.2816556 1.9658006
#> Trackway_03 3.0226495 2.0482129 NA 3.3187228 1.5737916
#> Trackway_04 0.4783721 1.2816556 3.3187228 NA 3.0996669
#> Trackway_07 3.1533083 1.9658006 1.5737916 3.0996669 NA
#> Trackway_08 4.4180593 3.5366716 3.1598612 4.4586918 1.7578290
#> Trackway_09 2.7031074 2.0786189 2.4830912 2.8758452 1.0121945
#> Trackway_13 2.1383919 1.5519100 2.1022240 2.3475549 0.9252769
#> Trackway_15 -1.0000000 -1.0000000 9.0863584 12.3996468 -1.0000000
#> Trackway_16 7.9724576 7.0422585 -1.0000000 -1.0000000 5.1292474
#> Trackway_18 3.0664193 2.0763751 0.4051164 3.3745924 1.1838016
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 4.418059 2.703107 2.1383919 -1.000000 7.972458
#> Trackway_02 3.536672 2.078619 1.5519100 -1.000000 7.042258
#> Trackway_03 3.159861 2.483091 2.1022240 9.086358 -1.000000
#> Trackway_04 4.458692 2.875845 2.3475549 12.399647 -1.000000
#> Trackway_07 1.757829 1.012195 0.9252769 -1.000000 5.129247
#> Trackway_08 NA 1.557750 2.1794367 9.613988 4.282196
#> Trackway_09 1.557750 NA 0.6334210 10.513269 5.615296
#> Trackway_13 2.179437 0.633421 NA 10.596786 5.958407
#> Trackway_15 9.613988 10.513269 10.5967861 NA -1.000000
#> Trackway_16 4.282196 5.615296 5.9584066 -1.000000 NA
#> Trackway_18 2.757094 2.162697 2.0575033 9.053812 -1.000000
#> Trackway_18
#> Trackway_01 3.0664193
#> Trackway_02 2.0763751
#> Trackway_03 0.4051164
#> Trackway_04 3.3745924
#> Trackway_07 1.1838016
#> Trackway_08 2.7570940
#> Trackway_09 2.1626973
#> Trackway_13 2.0575033
#> Trackway_15 9.0538115
#> Trackway_16 -1.0000000
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[38]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1.2551348 2.8981483 0.7768084 2.2647364
#> Trackway_02 1.2551348 NA 1.8027377 1.3356712 2.0104434
#> Trackway_03 2.8981483 1.8027377 NA 3.1235038 1.9399971
#> Trackway_04 0.7768084 1.3356712 3.1235038 NA 2.8744644
#> Trackway_07 2.2647364 2.0104434 1.9399971 2.8744644 NA
#> Trackway_08 2.6874105 2.0041438 1.0958615 3.1464192 1.0508895
#> Trackway_09 2.4478387 1.6404561 0.5964098 2.8723822 1.0818646
#> Trackway_13 1.8270556 0.8626678 1.0015514 2.3370205 1.4472402
#> Trackway_15 11.3101666 10.3492401 -1.0000000 11.6747658 -1.0000000
#> Trackway_16 7.3134023 6.8329038 5.2768143 7.9336388 -1.0000000
#> Trackway_18 2.7468409 2.2055689 1.1854300 3.3020323 0.7307607
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 2.6874105 2.4478387 1.8270556 11.310167 7.313402
#> Trackway_02 2.0041438 1.6404561 0.8626678 10.349240 6.832904
#> Trackway_03 1.0958615 0.5964098 1.0015514 -1.000000 5.276814
#> Trackway_04 3.1464192 2.8723822 2.3370205 11.674766 7.933639
#> Trackway_07 1.0508895 1.0818646 1.4472402 -1.000000 -1.000000
#> Trackway_08 NA 0.2987866 1.0777786 -1.000000 4.910088
#> Trackway_09 0.2987866 NA 0.7998268 8.862432 -1.000000
#> Trackway_13 1.0777786 0.7998268 NA 9.541587 5.986227
#> Trackway_15 -1.0000000 8.8624320 9.5415872 NA 5.601233
#> Trackway_16 4.9100879 -1.0000000 5.9862268 5.601233 NA
#> Trackway_18 0.4968016 0.7156691 1.4003182 8.669475 -1.000000
#> Trackway_18
#> Trackway_01 2.7468409
#> Trackway_02 2.2055689
#> Trackway_03 1.1854300
#> Trackway_04 3.3020323
#> Trackway_07 0.7307607
#> Trackway_08 0.4968016
#> Trackway_09 0.7156691
#> Trackway_13 1.4003182
#> Trackway_15 8.6694752
#> Trackway_16 -1.0000000
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[39]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1.660839 3.9331829 0.9043401 2.8970768
#> Trackway_02 1.6608394 NA 2.6693620 1.6904822 2.2951581
#> Trackway_03 3.9331829 2.669362 NA 4.2129665 1.5864882
#> Trackway_04 0.9043401 1.690482 4.2129665 NA 3.4662849
#> Trackway_07 2.8970768 2.295158 1.5864882 3.4662849 NA
#> Trackway_08 3.1359495 2.449132 1.4028362 3.6904593 0.3067048
#> Trackway_09 3.7293176 2.309521 0.9240191 3.8118548 2.0952655
#> Trackway_13 2.8945505 1.332924 1.3815794 2.8522949 1.4963704
#> Trackway_15 11.7113931 -1.000000 8.1434760 12.2188346 8.8143170
#> Trackway_16 7.0962102 6.861170 5.0232707 7.8558017 4.5671094
#> Trackway_18 3.6766907 2.657094 0.3413472 4.0090827 1.2628017
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.1359495 3.7293176 2.894550 11.711393 7.096210
#> Trackway_02 2.4491320 2.3095214 1.332924 -1.000000 6.861170
#> Trackway_03 1.4028362 0.9240191 1.381579 8.143476 5.023271
#> Trackway_04 3.6904593 3.8118548 2.852295 12.218835 7.855802
#> Trackway_07 0.3067048 2.0952655 1.496370 8.814317 4.567109
#> Trackway_08 NA 2.0000137 1.532192 -1.000000 4.434968
#> Trackway_09 2.0000137 NA 1.063254 8.867429 5.943986
#> Trackway_13 1.5321919 1.0632540 NA -1.000000 5.915732
#> Trackway_15 -1.0000000 8.8674286 -1.000000 NA -1.000000
#> Trackway_16 4.4349684 5.9439858 5.915732 -1.000000 NA
#> Trackway_18 1.0701408 1.0831666 1.242604 8.270388 -1.000000
#> Trackway_18
#> Trackway_01 3.6766907
#> Trackway_02 2.6570939
#> Trackway_03 0.3413472
#> Trackway_04 4.0090827
#> Trackway_07 1.2628017
#> Trackway_08 1.0701408
#> Trackway_09 1.0831666
#> Trackway_13 1.2426041
#> Trackway_15 8.2703875
#> Trackway_16 -1.0000000
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[40]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 2.5656973 4.1150565 2.2519647 2.5193859
#> Trackway_02 2.565697 NA 2.2774321 0.8540796 2.6041159
#> Trackway_03 4.115057 2.2774321 NA 2.9598035 2.5528992
#> Trackway_04 2.251965 0.8540796 2.9598035 NA 3.0876359
#> Trackway_07 2.519386 2.6041159 2.5528992 3.0876359 NA
#> Trackway_08 3.229135 2.5411064 1.6979981 3.2845450 0.9787875
#> Trackway_09 4.030372 1.9401602 0.4432524 2.8452597 2.6712053
#> Trackway_13 3.080552 1.1215629 1.2000023 1.9538072 2.0385049
#> Trackway_15 12.248708 -1.0000000 -1.0000000 11.9267800 9.7367170
#> Trackway_16 6.693822 6.6361233 5.2814400 7.3203949 4.3288586
#> Trackway_18 3.577105 2.4636595 1.3312530 3.1517123 1.3506652
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.2291349 4.0303722 3.0805521 12.248708 6.693822
#> Trackway_02 2.5411064 1.9401602 1.1215629 -1.000000 6.636123
#> Trackway_03 1.6979981 0.4432524 1.2000023 -1.000000 5.281440
#> Trackway_04 3.2845450 2.8452597 1.9538072 11.926780 7.320395
#> Trackway_07 0.9787875 2.6712053 2.0385049 9.736717 4.328859
#> Trackway_08 NA 1.7830016 1.4921677 -1.000000 4.245525
#> Trackway_09 1.7830016 NA 0.9612796 9.233870 -1.000000
#> Trackway_13 1.4921677 0.9612796 NA -1.000000 -1.000000
#> Trackway_15 -1.0000000 9.2338703 -1.0000000 NA 6.379734
#> Trackway_16 4.2455255 -1.0000000 -1.0000000 6.379734 NA
#> Trackway_18 0.4233261 1.4442843 1.3694824 8.907591 -1.000000
#> Trackway_18
#> Trackway_01 3.5771049
#> Trackway_02 2.4636595
#> Trackway_03 1.3312530
#> Trackway_04 3.1517123
#> Trackway_07 1.3506652
#> Trackway_08 0.4233261
#> Trackway_09 1.4442843
#> Trackway_13 1.3694824
#> Trackway_15 8.9075906
#> Trackway_16 -1.0000000
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[41]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1.0555340 3.1988545 0.5027637 2.7994989
#> Trackway_02 1.0555340 NA 2.3759261 1.5848956 2.1497354
#> Trackway_03 3.1988545 2.3759261 NA 3.3992119 0.9981348
#> Trackway_04 0.5027637 1.5848956 3.3992119 NA 3.0093714
#> Trackway_07 2.7994989 2.1497354 0.9981348 3.0093714 NA
#> Trackway_08 2.8747641 2.3709977 1.2064330 2.9373175 0.7705293
#> Trackway_09 2.6033909 1.7498239 0.6301790 2.9471455 0.7040980
#> Trackway_13 1.7460963 0.9036307 1.4827471 2.0389079 1.2623139
#> Trackway_15 11.7087955 -1.0000000 8.6783439 -1.0000000 8.9279463
#> Trackway_16 -1.0000000 7.3670702 -1.0000000 7.6117230 -1.0000000
#> Trackway_18 3.8953026 2.9981940 0.7901707 4.1442470 1.7187280
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 2.8747641 2.6033909 1.7460963 11.708795 -1.000000
#> Trackway_02 2.3709977 1.7498239 0.9036307 -1.000000 7.367070
#> Trackway_03 1.2064330 0.6301790 1.4827471 8.678344 -1.000000
#> Trackway_04 2.9373175 2.9471455 2.0389079 -1.000000 7.611723
#> Trackway_07 0.7705293 0.7040980 1.2623139 8.927946 -1.000000
#> Trackway_08 NA 1.1356272 1.5379505 -1.000000 4.999628
#> Trackway_09 1.1356272 NA 0.8683373 9.308331 -1.000000
#> Trackway_13 1.5379505 0.8683373 NA -1.000000 6.529519
#> Trackway_15 -1.0000000 9.3083311 -1.0000000 NA -1.000000
#> Trackway_16 4.9996284 -1.0000000 6.5295190 -1.000000 NA
#> Trackway_18 1.7462918 1.3100657 2.1525772 8.200032 5.335516
#> Trackway_18
#> Trackway_01 3.8953026
#> Trackway_02 2.9981940
#> Trackway_03 0.7901707
#> Trackway_04 4.1442470
#> Trackway_07 1.7187280
#> Trackway_08 1.7462918
#> Trackway_09 1.3100657
#> Trackway_13 2.1525772
#> Trackway_15 8.2000324
#> Trackway_16 5.3355157
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[42]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 5.089916 5.207069 2.370742 3.4462256
#> Trackway_02 5.089916 NA 2.073931 3.417448 2.7782940
#> Trackway_03 5.207069 2.073931 NA 4.427655 1.9184334
#> Trackway_04 2.370742 3.417448 4.427655 NA 3.2817639
#> Trackway_07 3.446226 2.778294 1.918433 3.281764 NA
#> Trackway_08 5.200288 2.323749 0.355381 4.533587 1.7828162
#> Trackway_09 3.122850 2.676797 2.084584 2.716113 0.7099055
#> Trackway_13 3.598186 1.704117 1.851663 2.579821 2.1277963
#> Trackway_15 -1.000000 -1.000000 8.408763 12.424531 9.1450688
#> Trackway_16 6.936773 -1.000000 5.509922 7.943785 4.9843219
#> Trackway_18 3.855995 2.676797 1.439873 3.850477 0.4242262
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 5.200288 3.1228502 3.5981863 -1.000000 6.936773
#> Trackway_02 2.323749 2.6767967 1.7041169 -1.000000 -1.000000
#> Trackway_03 0.355381 2.0845836 1.8516629 8.408763 5.509922
#> Trackway_04 4.533587 2.7161133 2.5798205 12.424531 7.943785
#> Trackway_07 1.782816 0.7099055 2.1277963 9.145069 4.984322
#> Trackway_08 NA 2.0859264 2.1247120 -1.000000 5.248365
#> Trackway_09 2.085926 NA 0.8717628 -1.000000 5.523950
#> Trackway_13 2.124712 0.8717628 NA -1.000000 6.189724
#> Trackway_15 -1.000000 -1.0000000 -1.0000000 NA -1.000000
#> Trackway_16 5.248365 5.5239500 6.1897237 -1.000000 NA
#> Trackway_18 1.362905 0.8444516 1.2993261 8.893187 4.983107
#> Trackway_18
#> Trackway_01 3.8559949
#> Trackway_02 2.6767967
#> Trackway_03 1.4398728
#> Trackway_04 3.8504767
#> Trackway_07 0.4242262
#> Trackway_08 1.3629055
#> Trackway_09 0.8444516
#> Trackway_13 1.2993261
#> Trackway_15 8.8931870
#> Trackway_16 4.9831066
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[43]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1.916313 4.6416650 0.7226681 2.6720285
#> Trackway_02 1.9163134 NA 2.7616728 2.5900007 1.6444092
#> Trackway_03 4.6416650 2.761673 NA 5.2684595 1.6568269
#> Trackway_04 0.7226681 2.590001 5.2684595 NA 3.4326147
#> Trackway_07 2.6720285 1.644409 1.6568269 3.4326147 NA
#> Trackway_08 3.2442149 2.168568 1.3731211 3.7420051 0.5393985
#> Trackway_09 3.7602849 2.124389 0.7047781 4.4882888 1.3668003
#> Trackway_13 2.8288525 1.310678 1.4812972 3.5827680 0.7659275
#> Trackway_15 12.0014916 -1.000000 8.4045754 12.4112867 9.5039791
#> Trackway_16 -1.0000000 -1.000000 5.0000871 7.4356563 5.2233801
#> Trackway_18 3.9163674 2.612454 0.3631436 4.5176685 1.2954681
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.2442149 3.7602849 2.8288525 12.001492 -1.000000
#> Trackway_02 2.1685682 2.1243894 1.3106783 -1.000000 -1.000000
#> Trackway_03 1.3731211 0.7047781 1.4812972 8.404575 5.000087
#> Trackway_04 3.7420051 4.4882888 3.5827680 12.411287 7.435656
#> Trackway_07 0.5393985 1.3668003 0.7659275 9.503979 5.223380
#> Trackway_08 NA 1.2967086 1.0079637 8.964591 4.758213
#> Trackway_09 1.2967086 NA 0.9321658 -1.000000 -1.000000
#> Trackway_13 1.0079637 0.9321658 NA 9.743674 5.754206
#> Trackway_15 8.9645909 -1.0000000 9.7436737 NA -1.000000
#> Trackway_16 4.7582126 -1.0000000 5.7542061 -1.000000 NA
#> Trackway_18 0.9716840 0.5965395 1.2043227 8.604886 -1.000000
#> Trackway_18
#> Trackway_01 3.9163674
#> Trackway_02 2.6124535
#> Trackway_03 0.3631436
#> Trackway_04 4.5176685
#> Trackway_07 1.2954681
#> Trackway_08 0.9716840
#> Trackway_09 0.5965395
#> Trackway_13 1.2043227
#> Trackway_15 8.6048858
#> Trackway_16 -1.0000000
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[44]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1.918538 3.8107647 1.607973 2.318445
#> Trackway_02 1.918538 NA 2.6573148 1.352942 2.619512
#> Trackway_03 3.810765 2.657315 NA 3.973848 1.969558
#> Trackway_04 1.607973 1.352942 3.9738478 NA 3.575490
#> Trackway_07 2.318445 2.619512 1.9695579 3.575490 NA
#> Trackway_08 3.161543 2.730999 0.9483306 3.860341 1.110008
#> Trackway_09 3.488780 2.483757 0.3607800 3.795358 1.915846
#> Trackway_13 2.649131 1.438962 1.2820068 2.694416 1.905322
#> Trackway_15 -1.000000 11.294219 8.6642915 -1.000000 -1.000000
#> Trackway_16 7.615256 7.923440 5.7809045 8.846192 -1.000000
#> Trackway_18 3.254890 2.666951 0.9351557 3.826634 1.212700
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.1615433 3.4887798 2.649131 -1.000000 7.615256
#> Trackway_02 2.7309993 2.4837568 1.438962 11.294219 7.923440
#> Trackway_03 0.9483306 0.3607800 1.282007 8.664291 5.780904
#> Trackway_04 3.8603415 3.7953577 2.694416 -1.000000 8.846192
#> Trackway_07 1.1100076 1.9158458 1.905322 -1.000000 -1.000000
#> Trackway_08 NA 0.9751364 1.544730 -1.000000 5.254242
#> Trackway_09 0.9751364 NA 1.068188 8.878623 5.953771
#> Trackway_13 1.5447301 1.0681879 NA 9.937035 6.795206
#> Trackway_15 -1.0000000 8.8786232 9.937035 NA -1.000000
#> Trackway_16 5.2542417 5.9537707 6.795206 -1.000000 NA
#> Trackway_18 0.2480361 0.8309742 1.442039 8.682994 -1.000000
#> Trackway_18
#> Trackway_01 3.2548901
#> Trackway_02 2.6669505
#> Trackway_03 0.9351557
#> Trackway_04 3.8266344
#> Trackway_07 1.2127004
#> Trackway_08 0.2480361
#> Trackway_09 0.8309742
#> Trackway_13 1.4420388
#> Trackway_15 8.6829939
#> Trackway_16 -1.0000000
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[45]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1.461757 2.9855249 0.5664462 2.3703357
#> Trackway_02 1.4617569 NA 2.0177677 2.0831311 1.8242846
#> Trackway_03 2.9855249 2.017768 NA 3.4609185 0.7367398
#> Trackway_04 0.5664462 2.083131 3.4609185 NA 2.9123722
#> Trackway_07 2.3703357 1.824285 0.7367398 2.9123722 NA
#> Trackway_08 2.9080176 3.044656 1.3013632 3.3951476 0.8589113
#> Trackway_09 2.9079957 1.741756 0.5978806 3.5460751 1.1793729
#> Trackway_13 1.9552613 1.064124 0.9830846 2.6761918 0.7883848
#> Trackway_15 11.7887021 10.901436 8.9567408 12.3280083 -1.0000000
#> Trackway_16 7.6035930 7.276907 5.3928787 8.0450001 5.4646720
#> Trackway_18 3.4194398 2.345532 0.8941989 3.9855711 1.3359442
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 2.9080176 2.9079957 1.9552613 11.788702 7.603593
#> Trackway_02 3.0446563 1.7417557 1.0641235 10.901436 7.276907
#> Trackway_03 1.3013632 0.5978806 0.9830846 8.956741 5.392879
#> Trackway_04 3.3951476 3.5460751 2.6761918 12.328008 8.045000
#> Trackway_07 0.8589113 1.1793729 0.7883848 -1.000000 5.464672
#> Trackway_08 NA 1.8800703 1.6419535 -1.000000 -1.000000
#> Trackway_09 1.8800703 NA 0.9765418 -1.000000 -1.000000
#> Trackway_13 1.6419535 0.9765418 NA -1.000000 6.214378
#> Trackway_15 -1.0000000 -1.0000000 -1.0000000 NA 5.518556
#> Trackway_16 -1.0000000 -1.0000000 6.2143780 5.518556 NA
#> Trackway_18 1.7796702 0.6387084 1.4651907 -1.000000 5.344730
#> Trackway_18
#> Trackway_01 3.4194398
#> Trackway_02 2.3455320
#> Trackway_03 0.8941989
#> Trackway_04 3.9855711
#> Trackway_07 1.3359442
#> Trackway_08 1.7796702
#> Trackway_09 0.6387084
#> Trackway_13 1.4651907
#> Trackway_15 -1.0000000
#> Trackway_16 5.3447305
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[46]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 2.164308 3.5861259 3.907330 2.917874
#> Trackway_02 2.164308 NA 2.1480130 1.937223 2.546039
#> Trackway_03 3.586126 2.148013 NA 3.200920 1.516085
#> Trackway_04 3.907330 1.937223 3.2009202 NA 4.211468
#> Trackway_07 2.917874 2.546039 1.5160853 4.211468 NA
#> Trackway_08 4.310599 3.015525 0.7260370 3.573619 2.010506
#> Trackway_09 4.230613 2.553583 0.9090361 3.159392 2.203206
#> Trackway_13 1.830616 1.768301 2.1113505 3.643681 1.246686
#> Trackway_15 11.916037 10.716540 -1.0000000 11.107562 -1.000000
#> Trackway_16 7.026029 6.600718 4.7804164 7.979879 4.114034
#> Trackway_18 4.218075 2.670906 0.6365892 3.395869 2.018139
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 4.3105992 4.2306130 1.830616 11.916037 7.026029
#> Trackway_02 3.0155253 2.5535829 1.768301 10.716540 6.600718
#> Trackway_03 0.7260370 0.9090361 2.111350 -1.000000 4.780416
#> Trackway_04 3.5736190 3.1593919 3.643681 11.107562 7.979879
#> Trackway_07 2.0105055 2.2032065 1.246686 -1.000000 4.114034
#> Trackway_08 NA 0.4231532 2.720201 7.915481 4.559882
#> Trackway_09 0.4231532 NA 2.732431 8.198016 4.982220
#> Trackway_13 2.7202012 2.7324306 NA -1.000000 5.272017
#> Trackway_15 7.9154813 8.1980158 -1.000000 NA 6.321538
#> Trackway_16 4.5598816 4.9822202 5.272017 6.321538 NA
#> Trackway_18 0.2851159 0.2769395 2.932299 8.061265 -1.000000
#> Trackway_18
#> Trackway_01 4.2180754
#> Trackway_02 2.6709062
#> Trackway_03 0.6365892
#> Trackway_04 3.3958687
#> Trackway_07 2.0181393
#> Trackway_08 0.2851159
#> Trackway_09 0.2769395
#> Trackway_13 2.9322990
#> Trackway_15 8.0612647
#> Trackway_16 -1.0000000
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[47]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0.6829869 2.9505468 0.6895481 2.478319
#> Trackway_02 0.6829869 NA 2.3366955 0.9881067 2.337546
#> Trackway_03 2.9505468 2.3366955 NA 3.3018203 2.252681
#> Trackway_04 0.6895481 0.9881067 3.3018203 NA 3.142328
#> Trackway_07 2.4783188 2.3375465 2.2526808 3.1423277 NA
#> Trackway_08 2.9583678 2.5870762 1.4493857 3.6026319 1.108736
#> Trackway_09 2.6566274 1.9570198 0.7417577 2.9434440 1.761698
#> Trackway_13 1.6991869 1.3388392 1.8699133 2.2700543 1.117525
#> Trackway_15 11.7005812 -1.0000000 8.9644648 12.1906018 9.588819
#> Trackway_16 7.2109764 6.9629683 5.4498497 7.8555928 -1.000000
#> Trackway_18 2.7696969 2.3039406 0.9447218 3.2840390 1.719552
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 2.9583678 2.6566274 1.699187 11.700581 7.210976
#> Trackway_02 2.5870762 1.9570198 1.338839 -1.000000 6.962968
#> Trackway_03 1.4493857 0.7417577 1.869913 8.964465 5.449850
#> Trackway_04 3.6026319 2.9434440 2.270054 12.190602 7.855593
#> Trackway_07 1.1087365 1.7616981 1.117525 9.588819 -1.000000
#> Trackway_08 NA 1.0994757 1.319773 8.794146 4.416658
#> Trackway_09 1.0994757 NA 1.036689 -1.000000 -1.000000
#> Trackway_13 1.3197732 1.0366886 NA -1.000000 -1.000000
#> Trackway_15 8.7941457 -1.0000000 -1.000000 NA 5.908653
#> Trackway_16 4.4166577 -1.0000000 -1.000000 5.908653 NA
#> Trackway_18 0.5209076 0.6741995 1.123797 8.930985 -1.000000
#> Trackway_18
#> Trackway_01 2.7696969
#> Trackway_02 2.3039406
#> Trackway_03 0.9447218
#> Trackway_04 3.2840390
#> Trackway_07 1.7195519
#> Trackway_08 0.5209076
#> Trackway_09 0.6741995
#> Trackway_13 1.1237973
#> Trackway_15 8.9309849
#> Trackway_16 -1.0000000
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[48]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1.7452625 3.4047047 1.260303 2.5067966
#> Trackway_02 1.745262 NA 2.0630800 2.022672 2.1025447
#> Trackway_03 3.404705 2.0630800 NA 4.049658 1.7594296
#> Trackway_04 1.260303 2.0226722 4.0496580 NA 3.5531872
#> Trackway_07 2.506797 2.1025447 1.7594296 3.553187 NA
#> Trackway_08 3.186356 1.9546194 0.9122967 3.897396 1.5711170
#> Trackway_09 2.005233 1.4434661 1.5098619 2.910497 0.7502474
#> Trackway_13 2.325422 0.7971549 1.3041532 2.745787 1.4856334
#> Trackway_15 11.611515 10.4489020 8.3869959 12.424579 9.1626332
#> Trackway_16 -1.000000 7.1445068 5.4584103 -1.000000 -1.0000000
#> Trackway_18 3.507600 2.1440152 0.1424262 4.266042 1.8025592
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.1863555 2.0052325 2.3254216 11.611515 -1.000000
#> Trackway_02 1.9546194 1.4434661 0.7971549 10.448902 7.144507
#> Trackway_03 0.9122967 1.5098619 1.3041532 8.386996 5.458410
#> Trackway_04 3.8973962 2.9104966 2.7457868 12.424579 -1.000000
#> Trackway_07 1.5711170 0.7502474 1.4856334 9.162633 -1.000000
#> Trackway_08 NA 1.3898670 1.1654952 8.527184 5.387815
#> Trackway_09 1.3898670 NA 0.9596551 9.610437 -1.000000
#> Trackway_13 1.1654952 0.9596551 NA -1.000000 -1.000000
#> Trackway_15 8.5271836 9.6104371 -1.0000000 NA -1.000000
#> Trackway_16 5.3878152 -1.0000000 -1.0000000 -1.000000 NA
#> Trackway_18 0.9122967 1.6326418 1.3951173 8.304907 5.447344
#> Trackway_18
#> Trackway_01 3.5076001
#> Trackway_02 2.1440152
#> Trackway_03 0.1424262
#> Trackway_04 4.2660417
#> Trackway_07 1.8025592
#> Trackway_08 0.9122967
#> Trackway_09 1.6326418
#> Trackway_13 1.3951173
#> Trackway_15 8.3049073
#> Trackway_16 5.4473435
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[49]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1.733765 2.5335155 0.8982783 2.7718899
#> Trackway_02 1.7337650 NA 2.9608572 2.6129666 1.9711166
#> Trackway_03 2.5335155 2.960857 NA 3.2519593 1.5241678
#> Trackway_04 0.8982783 2.612967 3.2519593 NA 3.3854259
#> Trackway_07 2.7718899 1.971117 1.5241678 3.3854259 NA
#> Trackway_08 3.5095682 2.732291 1.8187023 4.1642100 0.8089489
#> Trackway_09 2.7654711 3.621793 1.2016827 3.0917024 2.8249184
#> Trackway_13 1.5996126 1.798722 1.1134016 2.1781146 1.5284697
#> Trackway_15 11.2808680 11.412269 -1.0000000 11.7061123 9.5036231
#> Trackway_16 7.6106746 -1.000000 5.2406980 8.2223358 5.0565031
#> Trackway_18 2.8744438 3.734663 0.4404085 3.3627803 1.8913513
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.5095682 2.7654711 1.599613 11.280868 7.610675
#> Trackway_02 2.7322914 3.6217932 1.798722 11.412269 -1.000000
#> Trackway_03 1.8187023 1.2016827 1.113402 -1.000000 5.240698
#> Trackway_04 4.1642100 3.0917024 2.178115 11.706112 8.222336
#> Trackway_07 0.8089489 2.8249184 1.528470 9.503623 5.056503
#> Trackway_08 NA 2.9765394 2.094609 -1.000000 4.260140
#> Trackway_09 2.9765394 NA 1.896156 8.638061 5.867917
#> Trackway_13 2.0946087 1.8961559 NA 9.909413 -1.000000
#> Trackway_15 -1.0000000 8.6380610 9.909413 NA 5.717791
#> Trackway_16 4.2601401 5.8679166 -1.000000 5.717791 NA
#> Trackway_18 2.0503489 0.9543413 1.527246 8.417976 5.088251
#> Trackway_18
#> Trackway_01 2.8744438
#> Trackway_02 3.7346634
#> Trackway_03 0.4404085
#> Trackway_04 3.3627803
#> Trackway_07 1.8913513
#> Trackway_08 2.0503489
#> Trackway_09 0.9543413
#> Trackway_13 1.5272460
#> Trackway_15 8.4179761
#> Trackway_16 5.0882507
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[50]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 2.931767 3.9759259 2.806326 2.5384730
#> Trackway_02 2.931767 NA 2.1631200 1.306764 2.0693740
#> Trackway_03 3.975926 2.163120 NA 3.465523 1.6440165
#> Trackway_04 2.806326 1.306764 3.4655231 NA 3.0807405
#> Trackway_07 2.538473 2.069374 1.6440165 3.080740 NA
#> Trackway_08 3.169162 2.507495 1.2928321 3.637506 0.7726862
#> Trackway_09 2.574559 2.171645 1.8855444 3.158215 0.1184518
#> Trackway_13 2.253532 1.451143 1.7298133 2.407248 0.6808517
#> Trackway_15 11.305230 10.301566 8.1386104 -1.000000 8.9398435
#> Trackway_16 7.003621 7.194328 5.3706486 -1.000000 5.2386674
#> Trackway_18 3.771014 2.421138 0.7768934 3.620414 1.3240923
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.1691615 2.5745594 2.2535316 11.305230 7.003621
#> Trackway_02 2.5074945 2.1716453 1.4511430 10.301566 7.194328
#> Trackway_03 1.2928321 1.8855444 1.7298133 8.138610 5.370649
#> Trackway_04 3.6375055 3.1582147 2.4072479 -1.000000 -1.000000
#> Trackway_07 0.7726862 0.1184518 0.6808517 8.939843 5.238667
#> Trackway_08 NA 0.7300300 1.3416559 8.272683 4.693919
#> Trackway_09 0.7300300 NA 0.7612775 -1.000000 5.169269
#> Trackway_13 1.3416559 0.7612775 NA 9.511962 -1.000000
#> Trackway_15 8.2726834 -1.0000000 9.5119624 NA 5.218196
#> Trackway_16 4.6939187 5.1692687 -1.0000000 5.218196 NA
#> Trackway_18 0.9041531 1.3688828 1.5922502 -1.000000 4.981860
#> Trackway_18
#> Trackway_01 3.7710136
#> Trackway_02 2.4211379
#> Trackway_03 0.7768934
#> Trackway_04 3.6204144
#> Trackway_07 1.3240923
#> Trackway_08 0.9041531
#> Trackway_09 1.3688828
#> Trackway_13 1.5922502
#> Trackway_15 -1.0000000
#> Trackway_16 4.9818597
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[51]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 2.0034522 3.1962997 1.202943 2.4417445
#> Trackway_02 2.003452 NA 1.9061132 1.429327 2.0109210
#> Trackway_03 3.196300 1.9061132 NA 3.193225 1.2194770
#> Trackway_04 1.202943 1.4293274 3.1932252 NA 2.8596215
#> Trackway_07 2.441744 2.0109210 1.2194770 2.859621 NA
#> Trackway_08 2.809479 2.1893877 0.9497328 3.163130 0.3775082
#> Trackway_09 2.570694 3.1089250 2.5244111 3.462690 1.3868992
#> Trackway_13 2.265950 0.9144682 1.0513776 2.142243 1.1890050
#> Trackway_15 -1.000000 10.4126472 -1.0000000 -1.000000 -1.0000000
#> Trackway_16 -1.000000 6.9449466 5.1598920 7.914029 -1.0000000
#> Trackway_18 3.279858 2.2112598 0.3988201 3.546932 1.0148184
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 2.8094788 2.570694 2.2659504 -1.000000 -1.000000
#> Trackway_02 2.1893877 3.108925 0.9144682 10.412647 6.944947
#> Trackway_03 0.9497328 2.524411 1.0513776 -1.000000 5.159892
#> Trackway_04 3.1631296 3.462690 2.1422428 -1.000000 7.914029
#> Trackway_07 0.3775082 1.386899 1.1890050 -1.000000 -1.000000
#> Trackway_08 NA 1.583322 1.3006244 -1.000000 4.787128
#> Trackway_09 1.5833219 NA 2.5169888 9.690276 4.823205
#> Trackway_13 1.3006244 2.516989 NA -1.000000 6.031373
#> Trackway_15 -1.0000000 9.690276 -1.0000000 NA -1.000000
#> Trackway_16 4.7871285 4.823205 6.0313729 -1.000000 NA
#> Trackway_18 0.6977013 2.289369 1.3053710 8.394444 4.790333
#> Trackway_18
#> Trackway_01 3.2798579
#> Trackway_02 2.2112598
#> Trackway_03 0.3988201
#> Trackway_04 3.5469322
#> Trackway_07 1.0148184
#> Trackway_08 0.6977013
#> Trackway_09 2.2893686
#> Trackway_13 1.3053710
#> Trackway_15 8.3944435
#> Trackway_16 4.7903332
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[52]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 2.605100 4.6359723 1.057417 3.072225
#> Trackway_02 2.605100 NA 2.4668825 1.991137 1.963369
#> Trackway_03 4.635972 2.466883 NA 4.351531 1.898727
#> Trackway_04 1.057417 1.991137 4.3515308 NA 3.149940
#> Trackway_07 3.072225 1.963369 1.8987265 3.149940 NA
#> Trackway_08 4.647890 2.699713 0.3690885 4.398503 1.863608
#> Trackway_09 2.997585 1.375455 1.6678187 2.892748 0.643368
#> Trackway_13 3.319744 1.046616 1.4323224 2.932580 1.386398
#> Trackway_15 -1.000000 10.681194 8.4413395 -1.000000 8.982127
#> Trackway_16 -1.000000 -1.000000 -1.0000000 -1.000000 4.955782
#> Trackway_18 4.401803 2.473005 0.9466308 4.175379 1.588930
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 4.6478896 2.9975851 3.3197436 -1.000000 -1.000000
#> Trackway_02 2.6997134 1.3754546 1.0466163 10.681194 -1.000000
#> Trackway_03 0.3690885 1.6678187 1.4323224 8.441339 -1.000000
#> Trackway_04 4.3985032 2.8927482 2.9325799 -1.000000 -1.000000
#> Trackway_07 1.8636083 0.6433680 1.3863976 8.982127 4.955782
#> Trackway_08 NA 1.6631935 2.0357772 8.311890 5.357659
#> Trackway_09 1.6631935 NA 0.7818011 9.384382 5.551417
#> Trackway_13 2.0357772 0.7818011 NA 9.675193 -1.000000
#> Trackway_15 8.3118896 9.3843817 9.6751930 NA -1.000000
#> Trackway_16 5.3576590 5.5514173 -1.0000000 -1.000000 NA
#> Trackway_18 0.2557972 1.5165962 1.3096892 8.422362 -1.000000
#> Trackway_18
#> Trackway_01 4.4018027
#> Trackway_02 2.4730046
#> Trackway_03 0.9466308
#> Trackway_04 4.1753790
#> Trackway_07 1.5889297
#> Trackway_08 0.2557972
#> Trackway_09 1.5165962
#> Trackway_13 1.3096892
#> Trackway_15 8.4223620
#> Trackway_16 -1.0000000
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[53]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 4.806092 4.4846103 1.836067 2.7579897
#> Trackway_02 4.806092 NA 1.8321330 3.453627 2.6526559
#> Trackway_03 4.484610 1.832133 NA 3.774491 1.6701607
#> Trackway_04 1.836067 3.453627 3.7744911 NA 2.5419323
#> Trackway_07 2.757990 2.652656 1.6701607 2.541932 NA
#> Trackway_08 4.310515 2.569071 0.8088456 4.033496 1.5866853
#> Trackway_09 3.181467 1.808624 1.3433436 2.437256 0.8279177
#> Trackway_13 3.528051 1.354985 1.2834329 2.568309 1.2815348
#> Trackway_15 11.839105 10.287593 -1.0000000 -1.000000 9.6306722
#> Trackway_16 6.554798 6.938650 5.1704729 7.394229 5.0792302
#> Trackway_18 3.953653 2.341068 0.9406206 3.594431 1.1997365
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 4.3105148 3.1814674 3.5280509 11.839105 6.554798
#> Trackway_02 2.5690706 1.8086240 1.3549846 10.287593 6.938650
#> Trackway_03 0.8088456 1.3433436 1.2834329 -1.000000 5.170473
#> Trackway_04 4.0334958 2.4372558 2.5683093 -1.000000 7.394229
#> Trackway_07 1.5866853 0.8279177 1.2815348 9.630672 5.079230
#> Trackway_08 NA 1.6751986 1.8211975 8.241588 4.370023
#> Trackway_09 1.6751986 NA 0.4574339 -1.000000 5.707661
#> Trackway_13 1.8211975 0.4574339 NA 10.029921 6.028590
#> Trackway_15 8.2415882 -1.0000000 10.0299211 NA 5.713067
#> Trackway_16 4.3700235 5.7076609 6.0285899 5.713067 NA
#> Trackway_18 0.6209672 1.2296849 2.0333831 -1.000000 4.687250
#> Trackway_18
#> Trackway_01 3.9536534
#> Trackway_02 2.3410675
#> Trackway_03 0.9406206
#> Trackway_04 3.5944309
#> Trackway_07 1.1997365
#> Trackway_08 0.6209672
#> Trackway_09 1.2296849
#> Trackway_13 2.0333831
#> Trackway_15 -1.0000000
#> Trackway_16 4.6872498
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[54]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1.500171 4.0702589 0.6561425 2.5044846
#> Trackway_02 1.5001711 NA 2.9354296 2.1100796 1.8848261
#> Trackway_03 4.0702589 2.935430 NA 4.7215833 2.0953347
#> Trackway_04 0.6561425 2.110080 4.7215833 NA 3.3213187
#> Trackway_07 2.5044846 1.884826 2.0953347 3.3213187 NA
#> Trackway_08 3.0960097 2.593500 1.3109399 3.7264328 0.8479661
#> Trackway_09 3.9413449 2.472670 0.6047354 4.3885421 1.7161301
#> Trackway_13 3.4727367 2.103382 1.1459534 4.1242070 1.8696147
#> Trackway_15 11.8263436 -1.000000 8.3837224 12.3757163 -1.0000000
#> Trackway_16 7.2563829 7.154251 -1.0000000 7.6579352 -1.0000000
#> Trackway_18 3.3902006 2.438853 0.8037690 4.0297519 0.9881662
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.0960097 3.9413449 3.4727367 11.826344 7.256383
#> Trackway_02 2.5935004 2.4726696 2.1033816 -1.000000 7.154251
#> Trackway_03 1.3109399 0.6047354 1.1459534 8.383722 -1.000000
#> Trackway_04 3.7264328 4.3885421 4.1242070 12.375716 7.657935
#> Trackway_07 0.8479661 1.7161301 1.8696147 -1.000000 -1.000000
#> Trackway_08 NA 1.4225824 1.9947413 8.826483 4.938748
#> Trackway_09 1.4225824 NA 0.5414244 8.973121 -1.000000
#> Trackway_13 1.9947413 0.5414244 NA 9.506290 -1.000000
#> Trackway_15 8.8264834 8.9731210 9.5062904 NA 5.614853
#> Trackway_16 4.9387480 -1.0000000 -1.0000000 5.614853 NA
#> Trackway_18 0.5196825 1.0092750 1.3155415 8.715529 -1.000000
#> Trackway_18
#> Trackway_01 3.3902006
#> Trackway_02 2.4388528
#> Trackway_03 0.8037690
#> Trackway_04 4.0297519
#> Trackway_07 0.9881662
#> Trackway_08 0.5196825
#> Trackway_09 1.0092750
#> Trackway_13 1.3155415
#> Trackway_15 8.7155291
#> Trackway_16 -1.0000000
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[55]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 2.778771 2.7953018 1.702084 3.6050341
#> Trackway_02 2.778771 NA 3.3471131 1.300998 1.8850922
#> Trackway_03 2.795302 3.347113 NA 3.378880 2.5343480
#> Trackway_04 1.702084 1.300998 3.3788800 NA 2.8404129
#> Trackway_07 3.605034 1.885092 2.5343480 2.840413 NA
#> Trackway_08 3.846826 2.518369 2.2252860 3.343458 0.6790473
#> Trackway_09 2.545647 2.607797 0.7550611 2.755738 1.7838557
#> Trackway_13 1.721035 2.405618 1.2102752 2.166773 2.4054361
#> Trackway_15 -1.000000 11.815057 9.0578326 12.292235 10.0220089
#> Trackway_16 7.982294 6.738812 -1.0000000 7.671705 -1.0000000
#> Trackway_18 3.281183 3.835052 0.5924944 3.885309 2.7610710
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.8468255 2.5456473 1.7210350 -1.000000 7.982294
#> Trackway_02 2.5183689 2.6077970 2.4056184 11.815057 6.738812
#> Trackway_03 2.2252860 0.7550611 1.2102752 9.057833 -1.000000
#> Trackway_04 3.3434580 2.7557375 2.1667726 12.292235 7.671705
#> Trackway_07 0.6790473 1.7838557 2.4054361 10.022009 -1.000000
#> Trackway_08 NA 1.6164777 2.3690639 9.345778 4.328660
#> Trackway_09 1.6164777 NA 0.8337967 9.556130 -1.000000
#> Trackway_13 2.3690639 0.8337967 NA 10.256961 6.270042
#> Trackway_15 9.3457781 9.5561300 10.2569611 NA 6.240325
#> Trackway_16 4.3286599 -1.0000000 6.2700417 6.240325 NA
#> Trackway_18 2.3793685 1.2275990 1.7431150 -1.000000 -1.000000
#> Trackway_18
#> Trackway_01 3.2811832
#> Trackway_02 3.8350521
#> Trackway_03 0.5924944
#> Trackway_04 3.8853091
#> Trackway_07 2.7610710
#> Trackway_08 2.3793685
#> Trackway_09 1.2275990
#> Trackway_13 1.7431150
#> Trackway_15 -1.0000000
#> Trackway_16 -1.0000000
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[56]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1.291558 3.0114243 2.977629 2.7619654
#> Trackway_02 1.291558 NA 2.1976864 3.851858 2.7846058
#> Trackway_03 3.011424 2.197686 NA 4.775786 2.3210685
#> Trackway_04 2.977629 3.851858 4.7757863 NA 2.8152234
#> Trackway_07 2.761965 2.784606 2.3210685 2.815223 NA
#> Trackway_08 2.920393 2.446307 1.0899461 3.972090 1.5357107
#> Trackway_09 2.232736 2.133128 2.0869351 3.168014 0.7308274
#> Trackway_13 1.918368 1.536419 1.6561446 3.412101 1.3619517
#> Trackway_15 -1.000000 -1.000000 -1.0000000 12.764355 10.0092429
#> Trackway_16 8.289885 7.898857 -1.0000000 7.967127 -1.0000000
#> Trackway_18 2.830721 2.368765 0.9395371 4.275290 1.7141141
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 2.9203929 2.2327356 1.9183678 -1.000000 8.289885
#> Trackway_02 2.4463069 2.1331276 1.5364185 -1.000000 7.898857
#> Trackway_03 1.0899461 2.0869351 1.6561446 -1.000000 -1.000000
#> Trackway_04 3.9720898 3.1680140 3.4121007 12.764355 7.967127
#> Trackway_07 1.5357107 0.7308274 1.3619517 10.009243 -1.000000
#> Trackway_08 NA 1.0345859 1.0415430 9.143234 -1.000000
#> Trackway_09 1.0345859 NA 0.7144753 -1.000000 6.084485
#> Trackway_13 1.0415430 0.7144753 NA 10.086492 -1.000000
#> Trackway_15 9.1432337 -1.0000000 10.0864916 NA 5.767985
#> Trackway_16 -1.0000000 6.0844846 -1.0000000 5.767985 NA
#> Trackway_18 0.3072639 1.0685060 0.9164812 -1.000000 -1.000000
#> Trackway_18
#> Trackway_01 2.8307211
#> Trackway_02 2.3687645
#> Trackway_03 0.9395371
#> Trackway_04 4.2752904
#> Trackway_07 1.7141141
#> Trackway_08 0.3072639
#> Trackway_09 1.0685060
#> Trackway_13 0.9164812
#> Trackway_15 -1.0000000
#> Trackway_16 -1.0000000
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[57]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1.5301752 3.7523248 3.191803 2.7302740
#> Trackway_02 1.530175 NA 2.5020420 2.421471 1.9494972
#> Trackway_03 3.752325 2.5020420 NA 3.920105 1.6983645
#> Trackway_04 3.191803 2.4214709 3.9201050 NA 4.1931951
#> Trackway_07 2.730274 1.9494972 1.6983645 4.193195 NA
#> Trackway_08 3.952753 2.7120311 0.2892548 3.981945 1.9164371
#> Trackway_09 2.932432 1.6827016 0.8373864 3.568212 1.1291304
#> Trackway_13 2.003182 0.9959522 1.9186691 3.339504 0.9240032
#> Trackway_15 12.133051 -1.0000000 -1.0000000 12.322917 9.5186300
#> Trackway_16 7.628363 7.0079209 5.2282245 9.065657 5.1297907
#> Trackway_18 3.477677 2.2422677 0.4049464 3.969551 1.3033765
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.9527525 2.9324321 2.0031820 12.133051 7.628363
#> Trackway_02 2.7120311 1.6827016 0.9959522 -1.000000 7.007921
#> Trackway_03 0.2892548 0.8373864 1.9186691 -1.000000 5.228224
#> Trackway_04 3.9819451 3.5682119 3.3395043 12.322917 9.065657
#> Trackway_07 1.9164371 1.1291304 0.9240032 9.518630 5.129791
#> Trackway_08 NA 1.2535402 2.1320729 8.498015 -1.000000
#> Trackway_09 1.2535402 NA 1.0815668 9.327458 -1.000000
#> Trackway_13 2.1320729 1.0815668 NA -1.000000 6.047646
#> Trackway_15 8.4980155 9.3274582 -1.0000000 NA -1.000000
#> Trackway_16 -1.0000000 -1.0000000 6.0476455 -1.000000 NA
#> Trackway_18 1.0091642 0.5563737 2.0649148 -1.000000 5.106226
#> Trackway_18
#> Trackway_01 3.4776766
#> Trackway_02 2.2422677
#> Trackway_03 0.4049464
#> Trackway_04 3.9695513
#> Trackway_07 1.3033765
#> Trackway_08 1.0091642
#> Trackway_09 0.5563737
#> Trackway_13 2.0649148
#> Trackway_15 -1.0000000
#> Trackway_16 5.1062263
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[58]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 3.882759 5.3441226 4.361153 2.9434303
#> Trackway_02 3.882759 NA 2.3590034 1.250129 1.8625695
#> Trackway_03 5.344123 2.359003 NA 3.414452 2.4171341
#> Trackway_04 4.361153 1.250129 3.4144518 NA 3.0248028
#> Trackway_07 2.943430 1.862569 2.4171341 3.024803 NA
#> Trackway_08 3.568428 2.210576 1.9472512 3.432857 0.9490134
#> Trackway_09 4.278980 1.355843 1.1485956 2.558973 1.4522474
#> Trackway_13 4.480204 1.400843 1.1245548 2.429498 1.6621999
#> Trackway_15 11.422951 10.368476 8.1912095 -1.000000 9.2463414
#> Trackway_16 6.577198 6.906653 5.5699197 8.148561 -1.0000000
#> Trackway_18 5.299570 2.669859 0.5543765 3.946685 2.3147056
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.5684284 4.2789802 4.4802038 11.422951 6.577198
#> Trackway_02 2.2105759 1.3558428 1.4008427 10.368476 6.906653
#> Trackway_03 1.9472512 1.1485956 1.1245548 8.191209 5.569920
#> Trackway_04 3.4328569 2.5589732 2.4294984 -1.000000 8.148561
#> Trackway_07 0.9490134 1.4522474 1.6621999 9.246341 -1.000000
#> Trackway_08 NA 1.2795696 1.5035366 8.548399 4.716198
#> Trackway_09 1.2795696 NA 0.2311299 9.013568 5.757862
#> Trackway_13 1.5035366 0.2311299 NA -1.000000 -1.000000
#> Trackway_15 8.5483992 9.0135679 -1.0000000 NA 5.250192
#> Trackway_16 4.7161982 5.7578621 -1.0000000 5.250192 NA
#> Trackway_18 1.7213935 1.3373856 1.9160116 7.747624 -1.000000
#> Trackway_18
#> Trackway_01 5.2995705
#> Trackway_02 2.6698590
#> Trackway_03 0.5543765
#> Trackway_04 3.9466847
#> Trackway_07 2.3147056
#> Trackway_08 1.7213935
#> Trackway_09 1.3373856
#> Trackway_13 1.9160116
#> Trackway_15 7.7476241
#> Trackway_16 -1.0000000
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[59]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 3.832163 5.8155221 6.519623 3.6688791
#> Trackway_02 3.832163 NA 3.1527629 2.774872 2.0610458
#> Trackway_03 5.815522 3.152763 NA 3.517430 2.1684850
#> Trackway_04 6.519623 2.774872 3.5174295 NA 4.4855696
#> Trackway_07 3.668879 2.061046 2.1684850 4.485570 NA
#> Trackway_08 3.848674 2.240018 1.9919974 4.053234 0.3263025
#> Trackway_09 4.731886 1.476924 1.6955162 2.528502 1.4676245
#> Trackway_13 5.272942 2.048533 1.2304585 2.488498 1.8162525
#> Trackway_15 11.855111 10.932103 7.9937447 11.228552 -1.0000000
#> Trackway_16 5.706155 6.202496 -1.0000000 7.879054 4.4137750
#> Trackway_18 5.351904 2.805176 0.9877464 3.451815 1.6833382
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.8486741 4.731886 5.272942 11.855111 5.706155
#> Trackway_02 2.2400177 1.476924 2.048533 10.932103 6.202496
#> Trackway_03 1.9919974 1.695516 1.230459 7.993745 -1.000000
#> Trackway_04 4.0532342 2.528502 2.488498 11.228552 7.879054
#> Trackway_07 0.3263025 1.467624 1.816252 -1.000000 4.413775
#> Trackway_08 NA 1.607116 2.041553 8.875450 4.006586
#> Trackway_09 1.6071158 NA 0.613068 9.612165 5.487548
#> Trackway_13 2.0415535 0.613068 NA -1.000000 5.493313
#> Trackway_15 8.8754497 9.612165 -1.000000 NA 6.368712
#> Trackway_16 4.0065865 5.487548 5.493313 6.368712 NA
#> Trackway_18 1.5611760 1.439727 1.074385 -1.000000 -1.000000
#> Trackway_18
#> Trackway_01 5.3519042
#> Trackway_02 2.8051758
#> Trackway_03 0.9877464
#> Trackway_04 3.4518154
#> Trackway_07 1.6833382
#> Trackway_08 1.5611760
#> Trackway_09 1.4397267
#> Trackway_13 1.0743845
#> Trackway_15 -1.0000000
#> Trackway_16 -1.0000000
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[60]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 2.130586 3.5946793 0.9593543 2.1384143
#> Trackway_02 2.1305862 NA 2.3644196 1.8567708 2.2963095
#> Trackway_03 3.5946793 2.364420 NA 4.4017351 1.9638788
#> Trackway_04 0.9593543 1.856771 4.4017351 NA 2.8700990
#> Trackway_07 2.1384143 2.296310 1.9638788 2.8700990 NA
#> Trackway_08 3.2366394 2.754845 0.9838794 3.6851184 1.1561378
#> Trackway_09 1.8561430 1.953100 1.9008599 2.4439106 0.5429523
#> Trackway_13 2.0163338 1.498473 1.9930424 2.3478652 0.8150019
#> Trackway_15 -1.0000000 -1.000000 8.6366748 12.2184310 9.5022672
#> Trackway_16 6.9099329 7.151260 -1.0000000 7.7424581 5.0292290
#> Trackway_18 2.9359655 2.521044 1.2045154 3.4853178 0.9253247
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.2366394 1.8561430 2.0163338 -1.000000 6.909933
#> Trackway_02 2.7548453 1.9530999 1.4984728 -1.000000 7.151260
#> Trackway_03 0.9838794 1.9008599 1.9930424 8.636675 -1.000000
#> Trackway_04 3.6851184 2.4439106 2.3478652 12.218431 7.742458
#> Trackway_07 1.1561378 0.5429523 0.8150019 9.502267 5.029229
#> Trackway_08 NA 1.2954681 1.2776046 -1.000000 4.655352
#> Trackway_09 1.2954681 NA 0.4642121 9.785516 -1.000000
#> Trackway_13 1.2776046 0.4642121 NA -1.000000 5.704911
#> Trackway_15 -1.0000000 9.7855165 -1.0000000 NA -1.000000
#> Trackway_16 4.6553521 -1.0000000 5.7049105 -1.000000 NA
#> Trackway_18 0.2468561 1.0802496 1.1625694 8.733558 4.635070
#> Trackway_18
#> Trackway_01 2.9359655
#> Trackway_02 2.5210435
#> Trackway_03 1.2045154
#> Trackway_04 3.4853178
#> Trackway_07 0.9253247
#> Trackway_08 0.2468561
#> Trackway_09 1.0802496
#> Trackway_13 1.1625694
#> Trackway_15 8.7335579
#> Trackway_16 4.6350705
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[61]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1.661085 3.5644615 0.7208481 2.626296
#> Trackway_02 1.6610854 NA 2.2061284 2.4148821 2.065509
#> Trackway_03 3.5644615 2.206128 NA 4.0593304 1.718957
#> Trackway_04 0.7208481 2.414882 4.0593304 NA 2.785467
#> Trackway_07 2.6262957 2.065509 1.7189571 2.7854671 NA
#> Trackway_08 3.7080935 2.511485 0.8012089 3.8719320 1.303372
#> Trackway_09 3.2713248 1.742409 0.7645552 3.8592603 2.041158
#> Trackway_13 2.3762041 1.050825 1.3825609 2.6955666 1.128959
#> Trackway_15 -1.0000000 10.596598 -1.0000000 11.9028926 -1.000000
#> Trackway_16 -1.0000000 -1.000000 5.4352078 7.5673814 -1.000000
#> Trackway_18 3.5954122 2.352715 0.8490914 3.9437528 1.532804
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.7080935 3.2713248 2.376204 -1.000000 -1.000000
#> Trackway_02 2.5114850 1.7424088 1.050825 10.596598 -1.000000
#> Trackway_03 0.8012089 0.7645552 1.382561 -1.000000 5.435208
#> Trackway_04 3.8719320 3.8592603 2.695567 11.902893 7.567381
#> Trackway_07 1.3033719 2.0411580 1.128959 -1.000000 -1.000000
#> Trackway_08 NA 1.2011360 1.332394 8.312127 5.033999
#> Trackway_09 1.2011360 NA 1.224287 -1.000000 -1.000000
#> Trackway_13 1.3323944 1.2242873 NA 9.642296 -1.000000
#> Trackway_15 8.3121267 -1.0000000 9.642296 NA -1.000000
#> Trackway_16 5.0339991 -1.0000000 -1.000000 -1.000000 NA
#> Trackway_18 0.1218673 1.2044421 2.038474 8.252862 5.013136
#> Trackway_18
#> Trackway_01 3.5954122
#> Trackway_02 2.3527146
#> Trackway_03 0.8490914
#> Trackway_04 3.9437528
#> Trackway_07 1.5328043
#> Trackway_08 0.1218673
#> Trackway_09 1.2044421
#> Trackway_13 2.0384738
#> Trackway_15 8.2528624
#> Trackway_16 5.0131362
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[62]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 3.050858 4.6172978 4.881439 3.5226188
#> Trackway_02 3.050858 NA 2.2662554 2.015818 1.7275056
#> Trackway_03 4.617298 2.266255 NA 3.077092 1.1347741
#> Trackway_04 4.881439 2.015818 3.0770916 NA 3.4402332
#> Trackway_07 3.522619 1.727506 1.1347741 3.440233 NA
#> Trackway_08 3.791419 2.580892 1.3371711 3.933470 0.7080313
#> Trackway_09 5.257754 2.604023 0.8861735 2.748603 2.0329525
#> Trackway_13 4.808609 2.064521 0.7529454 2.411674 1.5928194
#> Trackway_15 -1.000000 10.510864 -1.0000000 11.105909 -1.0000000
#> Trackway_16 7.426479 -1.000000 -1.0000000 -1.000000 5.4840473
#> Trackway_18 4.410549 2.276601 0.8281679 3.499667 0.6890189
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.7914192 5.2577537 4.8086090 -1.000000 7.426479
#> Trackway_02 2.5808918 2.6040225 2.0645206 10.510864 -1.000000
#> Trackway_03 1.3371711 0.8861735 0.7529454 -1.000000 -1.000000
#> Trackway_04 3.9334703 2.7486028 2.4116738 11.105909 -1.000000
#> Trackway_07 0.7080313 2.0329525 1.5928194 -1.000000 5.484047
#> Trackway_08 NA 2.2181192 2.0022870 -1.000000 4.781861
#> Trackway_09 2.2181192 NA 0.4766906 8.414892 -1.000000
#> Trackway_13 2.0022870 0.4766906 NA -1.000000 6.304065
#> Trackway_15 -1.0000000 8.4148916 -1.0000000 NA 5.292270
#> Trackway_16 4.7818610 -1.0000000 6.3040647 5.292270 NA
#> Trackway_18 0.6566231 1.6093619 1.3790933 8.256524 5.114369
#> Trackway_18
#> Trackway_01 4.4105488
#> Trackway_02 2.2766010
#> Trackway_03 0.8281679
#> Trackway_04 3.4996666
#> Trackway_07 0.6890189
#> Trackway_08 0.6566231
#> Trackway_09 1.6093619
#> Trackway_13 1.3790933
#> Trackway_15 8.2565242
#> Trackway_16 5.1143695
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[63]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1.825839 4.1618656 2.068752 2.195139
#> Trackway_02 1.825839 NA 2.7564914 1.117826 1.551943
#> Trackway_03 4.161866 2.756491 NA 3.733059 2.214847
#> Trackway_04 2.068752 1.117826 3.7330590 NA 2.477175
#> Trackway_07 2.195139 1.551943 2.2148470 2.477175 NA
#> Trackway_08 2.593549 2.769847 2.6888995 3.639057 1.429799
#> Trackway_09 4.503277 3.056949 0.6020084 3.843437 2.638855
#> Trackway_13 2.928477 1.279372 2.0808388 2.265459 1.349784
#> Trackway_15 -1.000000 11.009643 -1.0000000 12.095119 9.872101
#> Trackway_16 6.409204 6.393037 4.9473591 7.492894 5.010377
#> Trackway_18 3.359520 2.268319 1.0408131 3.361347 1.484334
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 2.593549 4.5032773 2.928477 -1.000000 6.409204
#> Trackway_02 2.769847 3.0569493 1.279372 11.009643 6.393037
#> Trackway_03 2.688899 0.6020084 2.080839 -1.000000 4.947359
#> Trackway_04 3.639057 3.8434366 2.265459 12.095119 7.492894
#> Trackway_07 1.429799 2.6388549 1.349784 9.872101 5.010377
#> Trackway_08 NA 3.3082413 2.693473 -1.000000 3.929707
#> Trackway_09 3.308241 NA 1.687967 8.610149 -1.000000
#> Trackway_13 2.693473 1.6879667 NA -1.000000 -1.000000
#> Trackway_15 -1.000000 8.6101491 -1.000000 NA -1.000000
#> Trackway_16 3.929707 -1.0000000 -1.000000 -1.000000 NA
#> Trackway_18 1.765059 1.5745360 1.273380 8.741355 4.504703
#> Trackway_18
#> Trackway_01 3.359520
#> Trackway_02 2.268319
#> Trackway_03 1.040813
#> Trackway_04 3.361347
#> Trackway_07 1.484334
#> Trackway_08 1.765059
#> Trackway_09 1.574536
#> Trackway_13 1.273380
#> Trackway_15 8.741355
#> Trackway_16 4.504703
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[64]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1.132730 4.241795 2.114815 2.3018369
#> Trackway_02 1.132730 NA 3.392903 1.708005 1.5739498
#> Trackway_03 4.241795 3.392903 NA 4.157416 2.0474090
#> Trackway_04 2.114815 1.708005 4.157416 NA 3.0474296
#> Trackway_07 2.301837 1.573950 2.047409 3.047430 NA
#> Trackway_08 3.264326 2.431981 1.295363 3.887902 0.9845719
#> Trackway_09 3.154280 2.206414 1.070419 3.242242 1.1298971
#> Trackway_13 4.008874 2.966816 1.191480 3.386751 2.3273893
#> Trackway_15 -1.000000 11.138504 -1.000000 12.489066 9.5933522
#> Trackway_16 7.108154 6.820225 5.355909 -1.000000 5.4023967
#> Trackway_18 3.141472 2.369469 1.562011 3.898243 0.8573018
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.2643259 3.1542804 4.008874 -1.000000 7.108154
#> Trackway_02 2.4319813 2.2064145 2.966816 11.138504 6.820225
#> Trackway_03 1.2953628 1.0704189 1.191480 -1.000000 5.355909
#> Trackway_04 3.8879022 3.2422416 3.386751 12.489066 -1.000000
#> Trackway_07 0.9845719 1.1298971 2.327389 9.593352 5.402397
#> Trackway_08 NA 0.8279587 1.842052 8.785481 -1.000000
#> Trackway_09 0.8279587 NA 1.238830 -1.000000 5.657883
#> Trackway_13 1.8420525 1.2388301 NA -1.000000 6.526131
#> Trackway_15 8.7854806 -1.0000000 -1.000000 NA -1.000000
#> Trackway_16 -1.0000000 5.6578830 6.526131 -1.000000 NA
#> Trackway_18 0.2430778 0.8892910 2.071377 -1.000000 -1.000000
#> Trackway_18
#> Trackway_01 3.1414721
#> Trackway_02 2.3694686
#> Trackway_03 1.5620109
#> Trackway_04 3.8982432
#> Trackway_07 0.8573018
#> Trackway_08 0.2430778
#> Trackway_09 0.8892910
#> Trackway_13 2.0713771
#> Trackway_15 -1.0000000
#> Trackway_16 -1.0000000
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[65]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1.925714 3.0065454 0.7666684 2.5369735
#> Trackway_02 1.9257137 NA 2.1171881 2.6679566 2.6780008
#> Trackway_03 3.0065454 2.117188 NA 3.6754754 1.3279460
#> Trackway_04 0.7666684 2.667957 3.6754754 NA 2.9010722
#> Trackway_07 2.5369735 2.678001 1.3279460 2.9010722 NA
#> Trackway_08 3.2495126 2.874101 1.0561691 3.7346984 0.8358929
#> Trackway_09 2.4918476 1.427074 0.7077590 3.0593443 1.4428398
#> Trackway_13 2.3021190 1.720522 0.8830638 2.7160090 0.9128126
#> Trackway_15 -1.0000000 -1.000000 -1.0000000 -1.0000000 -1.0000000
#> Trackway_16 8.3099910 7.677746 -1.0000000 8.6714289 -1.0000000
#> Trackway_18 3.5612812 2.350448 0.7685810 4.2124790 2.0820289
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.2495126 2.4918476 2.3021190 -1.000000 8.309991
#> Trackway_02 2.8741005 1.4270735 1.7205221 -1.000000 7.677746
#> Trackway_03 1.0561691 0.7077590 0.8830638 -1.000000 -1.000000
#> Trackway_04 3.7346984 3.0593443 2.7160090 -1.000000 8.671429
#> Trackway_07 0.8358929 1.4428398 0.9128126 -1.000000 -1.000000
#> Trackway_08 NA 1.4777012 1.2198462 -1.000000 -1.000000
#> Trackway_09 1.4777012 NA 0.5871474 9.528493 6.284452
#> Trackway_13 1.2198462 0.5871474 NA 9.762110 6.246505
#> Trackway_15 -1.0000000 9.5284925 9.7621102 NA 5.104990
#> Trackway_16 -1.0000000 6.2844522 6.2465047 5.104990 NA
#> Trackway_18 1.7672913 1.1557616 1.5733303 8.411779 5.483963
#> Trackway_18
#> Trackway_01 3.561281
#> Trackway_02 2.350448
#> Trackway_03 0.768581
#> Trackway_04 4.212479
#> Trackway_07 2.082029
#> Trackway_08 1.767291
#> Trackway_09 1.155762
#> Trackway_13 1.573330
#> Trackway_15 8.411779
#> Trackway_16 5.483963
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[66]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 3.234022 4.5476111 3.004361 2.5248619
#> Trackway_02 3.234022 NA 2.4336691 1.836772 1.8249906
#> Trackway_03 4.547611 2.433669 NA 4.260205 2.0317959
#> Trackway_04 3.004361 1.836772 4.2602048 NA 3.1258917
#> Trackway_07 2.524862 1.824991 2.0317959 3.125892 NA
#> Trackway_08 3.300324 2.202174 1.3700045 3.773870 0.8176971
#> Trackway_09 2.978092 1.660913 1.6848394 3.081878 0.7084221
#> Trackway_13 3.402755 1.145458 1.4026537 2.903474 1.1155516
#> Trackway_15 11.795022 10.786792 -1.0000000 12.578811 9.6898776
#> Trackway_16 7.022354 -1.000000 -1.0000000 -1.000000 5.5862697
#> Trackway_18 4.169092 2.258360 0.3958916 4.052194 1.7899061
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.3003237 2.9780923 3.4027546 11.795022 7.022354
#> Trackway_02 2.2021738 1.6609128 1.1454578 10.786792 -1.000000
#> Trackway_03 1.3700045 1.6848394 1.4026537 -1.000000 -1.000000
#> Trackway_04 3.7738698 3.0818784 2.9034739 12.578811 -1.000000
#> Trackway_07 0.8176971 0.7084221 1.1155516 9.689878 5.586270
#> Trackway_08 NA 0.7258865 1.1329511 8.907532 -1.000000
#> Trackway_09 0.7258865 NA 0.6574183 9.564345 5.736585
#> Trackway_13 1.1329511 0.6574183 NA -1.000000 6.125314
#> Trackway_15 8.9075325 9.5643449 -1.0000000 NA 5.431646
#> Trackway_16 -1.0000000 5.7365853 6.1253140 5.431646 NA
#> Trackway_18 0.9756695 1.2266180 1.1508009 -1.000000 5.249164
#> Trackway_18
#> Trackway_01 4.1690916
#> Trackway_02 2.2583602
#> Trackway_03 0.3958916
#> Trackway_04 4.0521942
#> Trackway_07 1.7899061
#> Trackway_08 0.9756695
#> Trackway_09 1.2266180
#> Trackway_13 1.1508009
#> Trackway_15 -1.0000000
#> Trackway_16 5.2491644
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[67]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1.384955 4.2227246 1.151233 2.6629451
#> Trackway_02 1.384955 NA 3.2962868 1.092629 2.3128016
#> Trackway_03 4.222725 3.296287 NA 4.270249 2.1655396
#> Trackway_04 1.151233 1.092629 4.2702492 NA 3.2493898
#> Trackway_07 2.662945 2.312802 2.1655396 3.249390 NA
#> Trackway_08 3.920784 3.057585 0.7789385 4.142538 1.5967398
#> Trackway_09 1.919891 1.218664 2.5207235 2.405820 1.1114680
#> Trackway_13 3.603796 2.514007 1.0248315 3.463192 2.3846522
#> Trackway_15 11.600265 11.230148 8.5936997 12.237361 8.9985231
#> Trackway_16 6.838550 6.949219 5.5747599 7.745284 -1.0000000
#> Trackway_18 2.971485 2.402011 2.1458949 3.441626 0.1306597
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.9207838 1.919891 3.603796 11.600265 6.838550
#> Trackway_02 3.0575855 1.218664 2.514007 11.230148 6.949219
#> Trackway_03 0.7789385 2.520723 1.024832 8.593700 5.574760
#> Trackway_04 4.1425385 2.405820 3.463192 12.237361 7.745284
#> Trackway_07 1.5967398 1.111468 2.384652 8.998523 -1.000000
#> Trackway_08 NA 2.037278 1.877027 -1.000000 4.998514
#> Trackway_09 2.0372782 NA 1.895761 10.021419 5.785160
#> Trackway_13 1.8770268 1.895761 NA -1.000000 -1.000000
#> Trackway_15 -1.0000000 10.021419 -1.000000 NA 5.503240
#> Trackway_16 4.9985144 5.785160 -1.000000 5.503240 NA
#> Trackway_18 1.5577968 1.192088 2.189214 8.891833 4.612177
#> Trackway_18
#> Trackway_01 2.9714849
#> Trackway_02 2.4020108
#> Trackway_03 2.1458949
#> Trackway_04 3.4416256
#> Trackway_07 0.1306597
#> Trackway_08 1.5577968
#> Trackway_09 1.1920877
#> Trackway_13 2.1892144
#> Trackway_15 8.8918335
#> Trackway_16 4.6121774
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[68]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 2.499593 4.4315762 4.241777 2.4030392
#> Trackway_02 2.499593 NA 2.4447486 1.823528 2.4640174
#> Trackway_03 4.431576 2.444749 NA 3.019633 2.4302883
#> Trackway_04 4.241777 1.823528 3.0196331 NA 4.0577977
#> Trackway_07 2.403039 2.464017 2.4302883 4.057798 NA
#> Trackway_08 3.874700 2.665816 0.8813492 3.531481 1.8229295
#> Trackway_09 3.317802 1.472385 0.9740151 2.443194 1.9274968
#> Trackway_13 2.167091 1.915157 2.2216758 3.599406 0.5221555
#> Trackway_15 -1.000000 11.302789 -1.0000000 11.678547 9.8690688
#> Trackway_16 7.158871 7.267069 5.4653431 -1.000000 5.0889223
#> Trackway_18 3.983950 2.636914 0.7317792 3.668426 1.7807685
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.8746997 3.3178023 2.1670909 -1.000000 7.158871
#> Trackway_02 2.6658160 1.4723851 1.9151565 11.302789 7.267069
#> Trackway_03 0.8813492 0.9740151 2.2216758 -1.000000 5.465343
#> Trackway_04 3.5314814 2.4431937 3.5994064 11.678547 -1.000000
#> Trackway_07 1.8229295 1.9274968 0.5221555 9.869069 5.088922
#> Trackway_08 NA 1.2062703 1.8651400 8.701545 4.901237
#> Trackway_09 1.2062703 NA 1.6338788 9.834694 -1.000000
#> Trackway_13 1.8651400 1.6338788 NA 10.228787 5.583031
#> Trackway_15 8.7015445 9.8346940 10.2287872 NA 5.865492
#> Trackway_16 4.9012369 -1.0000000 5.5830308 5.865492 NA
#> Trackway_18 0.1826684 1.2333080 1.8324116 8.697230 4.859752
#> Trackway_18
#> Trackway_01 3.9839496
#> Trackway_02 2.6369140
#> Trackway_03 0.7317792
#> Trackway_04 3.6684262
#> Trackway_07 1.7807685
#> Trackway_08 0.1826684
#> Trackway_09 1.2333080
#> Trackway_13 1.8324116
#> Trackway_15 8.6972300
#> Trackway_16 4.8597517
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[69]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0.8217655 3.615863 0.9011191 2.5611542
#> Trackway_02 0.8217655 NA 3.366919 1.7024069 1.9407011
#> Trackway_03 3.6158635 3.3669187 NA 3.7836310 2.0124837
#> Trackway_04 0.9011191 1.7024069 3.783631 NA 3.1936660
#> Trackway_07 2.5611542 1.9407011 2.012484 3.1936660 NA
#> Trackway_08 3.2260475 2.5203871 2.815729 3.9194600 0.7677870
#> Trackway_09 2.1320186 1.5191298 2.171207 2.7840929 0.4498196
#> Trackway_13 1.4016280 0.9149236 2.501357 2.0448914 1.1670035
#> Trackway_15 11.7204350 -1.0000000 8.431936 -1.0000000 9.2397064
#> Trackway_16 7.8486266 7.1042912 -1.000000 8.5446684 -1.0000000
#> Trackway_18 3.1406221 2.7716266 0.786041 3.4966183 1.3505414
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.226047 2.1320186 1.4016280 11.720435 7.848627
#> Trackway_02 2.520387 1.5191298 0.9149236 -1.000000 7.104291
#> Trackway_03 2.815729 2.1712074 2.5013572 8.431936 -1.000000
#> Trackway_04 3.919460 2.7840929 2.0448914 -1.000000 8.544668
#> Trackway_07 0.767787 0.4498196 1.1670035 9.239706 -1.000000
#> Trackway_08 NA 1.1387707 1.8747664 8.769283 4.630510
#> Trackway_09 1.138771 NA 0.7442451 9.660122 5.760855
#> Trackway_13 1.874766 0.7442451 NA -1.000000 6.502859
#> Trackway_15 8.769283 9.6601218 -1.0000000 NA 5.498973
#> Trackway_16 4.630510 5.7608555 6.5028595 5.498973 NA
#> Trackway_18 1.625216 1.4312181 1.8573839 8.634040 5.472093
#> Trackway_18
#> Trackway_01 3.140622
#> Trackway_02 2.771627
#> Trackway_03 0.786041
#> Trackway_04 3.496618
#> Trackway_07 1.350541
#> Trackway_08 1.625216
#> Trackway_09 1.431218
#> Trackway_13 1.857384
#> Trackway_15 8.634040
#> Trackway_16 5.472093
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[70]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0.9647156 3.0458944 1.418499 2.3878808
#> Trackway_02 0.9647156 NA 2.7419315 1.407422 1.6321158
#> Trackway_03 3.0458944 2.7419315 NA 4.116365 1.7091852
#> Trackway_04 1.4184987 1.4074217 4.1163654 NA 3.0286024
#> Trackway_07 2.3878808 1.6321158 1.7091852 3.028602 NA
#> Trackway_08 2.9662017 2.7302704 0.2578021 4.196998 1.4190563
#> Trackway_09 2.1707229 1.8523479 0.9106767 3.233423 0.7690872
#> Trackway_13 1.8655854 1.7697517 1.4224154 3.006690 1.3817128
#> Trackway_15 11.6047745 11.2357248 -1.0000000 -1.000000 -1.0000000
#> Trackway_16 -1.0000000 -1.0000000 4.9071335 -1.000000 -1.0000000
#> Trackway_18 3.1722772 2.9304951 0.9015470 4.280926 1.8733419
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 2.9662017 2.1707229 1.8655854 11.604774 -1.000000
#> Trackway_02 2.7302704 1.8523479 1.7697517 11.235725 -1.000000
#> Trackway_03 0.2578021 0.9106767 1.4224154 -1.000000 4.907134
#> Trackway_04 4.1969984 3.2334231 3.0066903 -1.000000 -1.000000
#> Trackway_07 1.4190563 0.7690872 1.3817128 -1.000000 -1.000000
#> Trackway_08 NA 0.9181523 1.9793601 8.638860 -1.000000
#> Trackway_09 0.9181523 NA 0.7343099 9.454863 5.562579
#> Trackway_13 1.9793601 0.7343099 NA -1.000000 6.262849
#> Trackway_15 8.6388602 9.4548629 -1.0000000 NA 5.934816
#> Trackway_16 -1.0000000 5.5625787 6.2628487 5.934816 NA
#> Trackway_18 0.9691909 1.1597131 1.3639180 8.535681 5.237711
#> Trackway_18
#> Trackway_01 3.1722772
#> Trackway_02 2.9304951
#> Trackway_03 0.9015470
#> Trackway_04 4.2809255
#> Trackway_07 1.8733419
#> Trackway_08 0.9691909
#> Trackway_09 1.1597131
#> Trackway_13 1.3639180
#> Trackway_15 8.5356806
#> Trackway_16 5.2377114
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[71]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0.6410173 3.1826550 1.682449 2.5533773
#> Trackway_02 0.6410173 NA 2.5421091 2.275254 1.9965878
#> Trackway_03 3.1826550 2.5421091 NA 4.767057 1.5108614
#> Trackway_04 1.6824494 2.2752537 4.7670569 NA 3.8243105
#> Trackway_07 2.5533773 1.9965878 1.5108614 3.824310 NA
#> Trackway_08 3.1651283 2.5018818 0.7891291 4.600225 0.9822994
#> Trackway_09 2.3162760 1.6752809 0.8736262 3.894107 1.0997908
#> Trackway_13 1.6350799 1.0840545 1.6002308 3.169143 1.1117540
#> Trackway_15 11.1651979 10.5271745 -1.0000000 -1.000000 8.8197457
#> Trackway_16 -1.0000000 -1.0000000 -1.0000000 -1.000000 5.1206212
#> Trackway_18 3.2997526 2.6938155 0.1429261 5.135208 1.6229707
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.1651283 2.3162760 1.6350799 11.165198 -1.000000
#> Trackway_02 2.5018818 1.6752809 1.0840545 10.527174 -1.000000
#> Trackway_03 0.7891291 0.8736262 1.6002308 -1.000000 -1.000000
#> Trackway_04 4.6002247 3.8941074 3.1691429 -1.000000 -1.000000
#> Trackway_07 0.9822994 1.0997908 1.1117540 8.819746 5.120621
#> Trackway_08 NA 0.9259542 1.4973219 -1.000000 4.873234
#> Trackway_09 0.9259542 NA 0.7316813 8.859915 5.785830
#> Trackway_13 1.4973219 0.7316813 NA 9.532565 6.182922
#> Trackway_15 -1.0000000 8.8599148 9.5325653 NA -1.000000
#> Trackway_16 4.8732335 5.7858300 6.1829219 -1.000000 NA
#> Trackway_18 0.8435537 1.0037045 1.7242949 7.913289 -1.000000
#> Trackway_18
#> Trackway_01 3.2997526
#> Trackway_02 2.6938155
#> Trackway_03 0.1429261
#> Trackway_04 5.1352082
#> Trackway_07 1.6229707
#> Trackway_08 0.8435537
#> Trackway_09 1.0037045
#> Trackway_13 1.7242949
#> Trackway_15 7.9132893
#> Trackway_16 -1.0000000
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[72]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1.668063 3.8129080 1.757280 2.9116987
#> Trackway_02 1.668063 NA 2.5775973 1.304046 2.2445326
#> Trackway_03 3.812908 2.577597 NA 3.743867 1.6019805
#> Trackway_04 1.757280 1.304046 3.7438667 NA 3.2864821
#> Trackway_07 2.911699 2.244533 1.6019805 3.286482 NA
#> Trackway_08 3.203015 2.635185 1.7302935 3.934492 0.7556904
#> Trackway_09 3.330507 2.008832 0.9784258 2.905814 1.8498562
#> Trackway_13 2.243984 1.010921 1.6007905 2.277632 1.1940044
#> Trackway_15 -1.000000 11.091758 -1.0000000 -1.000000 -1.0000000
#> Trackway_16 7.269050 6.764291 4.7866613 8.068330 -1.0000000
#> Trackway_18 3.540113 2.390549 0.9759016 3.637972 1.1011048
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.2030153 3.3305075 2.243984 -1.000000 7.269050
#> Trackway_02 2.6351855 2.0088323 1.010921 11.091758 6.764291
#> Trackway_03 1.7302935 0.9784258 1.600791 -1.000000 4.786661
#> Trackway_04 3.9344915 2.9058144 2.277632 -1.000000 8.068330
#> Trackway_07 0.7556904 1.8498562 1.194004 -1.000000 -1.000000
#> Trackway_08 NA 2.3969767 1.791221 -1.000000 4.154087
#> Trackway_09 2.3969767 NA 1.143721 9.387784 5.749503
#> Trackway_13 1.7912211 1.1437211 NA 10.086980 5.828689
#> Trackway_15 -1.0000000 9.3877840 10.086980 NA 5.883031
#> Trackway_16 4.1540869 5.7495026 5.828689 5.883031 NA
#> Trackway_18 1.1971632 1.2007468 1.435136 -1.000000 -1.000000
#> Trackway_18
#> Trackway_01 3.5401132
#> Trackway_02 2.3905488
#> Trackway_03 0.9759016
#> Trackway_04 3.6379716
#> Trackway_07 1.1011048
#> Trackway_08 1.1971632
#> Trackway_09 1.2007468
#> Trackway_13 1.4351361
#> Trackway_15 -1.0000000
#> Trackway_16 -1.0000000
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[73]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0.9480951 2.9619982 0.707895 2.764284
#> Trackway_02 0.9480951 NA 2.5632061 1.626331 1.752995
#> Trackway_03 2.9619982 2.5632061 NA 3.395219 2.600435
#> Trackway_04 0.7078950 1.6263312 3.3952187 NA 3.461733
#> Trackway_07 2.7642839 1.7529948 2.6004347 3.461733 NA
#> Trackway_08 3.2047854 2.5461699 1.1150582 3.788469 1.696407
#> Trackway_09 2.4434163 1.7224228 1.4709873 3.141819 1.176350
#> Trackway_13 1.7163250 1.0577118 1.6811855 2.329405 1.501593
#> Trackway_15 -1.0000000 11.0441942 8.7131693 12.108305 9.999074
#> Trackway_16 7.7494112 6.9354372 5.6601460 8.452408 5.333722
#> Trackway_18 2.7925407 2.3507476 0.5743144 3.475727 2.187986
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.2047854 2.4434163 1.7163250 -1.000000 7.749411
#> Trackway_02 2.5461699 1.7224228 1.0577118 11.044194 6.935437
#> Trackway_03 1.1150582 1.4709873 1.6811855 8.713169 5.660146
#> Trackway_04 3.7884690 3.1418190 2.3294047 12.108305 8.452408
#> Trackway_07 1.6964074 1.1763502 1.5015932 9.999074 5.333722
#> Trackway_08 NA 0.7753667 1.3284130 -1.000000 -1.000000
#> Trackway_09 0.7753667 NA 0.8213653 -1.000000 -1.000000
#> Trackway_13 1.3284130 0.8213653 NA -1.000000 6.132383
#> Trackway_15 -1.0000000 -1.0000000 -1.0000000 NA 5.987778
#> Trackway_16 -1.0000000 -1.0000000 6.1323832 5.987778 NA
#> Trackway_18 0.5671349 0.9968962 1.4147301 8.742717 5.327043
#> Trackway_18
#> Trackway_01 2.7925407
#> Trackway_02 2.3507476
#> Trackway_03 0.5743144
#> Trackway_04 3.4757267
#> Trackway_07 2.1879865
#> Trackway_08 0.5671349
#> Trackway_09 0.9968962
#> Trackway_13 1.4147301
#> Trackway_15 8.7427175
#> Trackway_16 5.3270432
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[74]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1.481965 3.0597430 2.380213 3.059887
#> Trackway_02 1.481965 NA 1.8895348 3.579121 2.975005
#> Trackway_03 3.059743 1.889535 NA 4.498331 2.094163
#> Trackway_04 2.380213 3.579121 4.4983313 NA 3.016658
#> Trackway_07 3.059887 2.975005 2.0941627 3.016658 NA
#> Trackway_08 3.561564 2.553877 0.7144834 4.636526 2.386154
#> Trackway_09 2.204291 1.437472 0.9048609 3.329734 1.633542
#> Trackway_13 1.628122 1.548542 1.5717822 2.743031 1.477249
#> Trackway_15 -1.000000 -1.000000 -1.0000000 -1.000000 9.904730
#> Trackway_16 -1.000000 7.742368 -1.0000000 8.564290 5.640524
#> Trackway_18 3.353650 2.231817 0.4262959 4.825549 2.260380
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.5615638 2.2042905 1.6281216 -1.000000 -1.000000
#> Trackway_02 2.5538769 1.4374723 1.5485419 -1.000000 7.742368
#> Trackway_03 0.7144834 0.9048609 1.5717822 -1.000000 -1.000000
#> Trackway_04 4.6365260 3.3297338 2.7430306 -1.000000 8.564290
#> Trackway_07 2.3861537 1.6335422 1.4772491 9.904730 5.640524
#> Trackway_08 NA 1.4515712 2.0563843 -1.000000 -1.000000
#> Trackway_09 1.4515712 NA 0.6703069 9.950976 6.424071
#> Trackway_13 2.0563843 0.6703069 NA 10.527623 -1.000000
#> Trackway_15 -1.0000000 9.9509763 10.5276230 NA 5.330025
#> Trackway_16 -1.0000000 6.4240713 -1.0000000 5.330025 NA
#> Trackway_18 0.3973244 1.3530314 2.0537437 8.705908 -1.000000
#> Trackway_18
#> Trackway_01 3.3536496
#> Trackway_02 2.2318171
#> Trackway_03 0.4262959
#> Trackway_04 4.8255487
#> Trackway_07 2.2603798
#> Trackway_08 0.3973244
#> Trackway_09 1.3530314
#> Trackway_13 2.0537437
#> Trackway_15 8.7059085
#> Trackway_16 -1.0000000
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[75]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 2.620189 3.746499 2.256643 2.2114717
#> Trackway_02 2.620189 NA 2.049235 1.456716 2.2051765
#> Trackway_03 3.746499 2.049235 NA 3.319242 1.7230182
#> Trackway_04 2.256643 1.456716 3.319242 NA 2.9622525
#> Trackway_07 2.211472 2.205176 1.723018 2.962253 NA
#> Trackway_08 3.272265 2.483952 1.014060 3.698287 1.0624882
#> Trackway_09 2.382433 1.622583 1.184968 2.690185 0.5402202
#> Trackway_13 2.027098 1.500799 2.078864 2.346857 0.6668201
#> Trackway_15 11.858982 10.687739 8.802784 12.120054 9.6741399
#> Trackway_16 6.730519 6.745063 -1.000000 -1.000000 4.9276766
#> Trackway_18 3.348319 2.493634 1.105753 3.730649 1.1412773
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.2722646 2.3824333 2.0270985 11.858982 6.730519
#> Trackway_02 2.4839515 1.6225832 1.5007987 10.687739 6.745063
#> Trackway_03 1.0140600 1.1849680 2.0788638 8.802784 -1.000000
#> Trackway_04 3.6982872 2.6901851 2.3468574 12.120054 -1.000000
#> Trackway_07 1.0624882 0.5402202 0.6668201 9.674140 4.927677
#> Trackway_08 NA 1.0897031 1.4239582 8.646039 -1.000000
#> Trackway_09 1.0897031 NA 0.3961571 9.657418 -1.000000
#> Trackway_13 1.4239582 0.3961571 NA 10.053519 5.524596
#> Trackway_15 8.6460393 9.6574182 10.0535190 NA -1.000000
#> Trackway_16 -1.0000000 -1.0000000 5.5245961 -1.000000 NA
#> Trackway_18 0.1487471 1.0843279 1.4773603 8.583331 -1.000000
#> Trackway_18
#> Trackway_01 3.3483189
#> Trackway_02 2.4936344
#> Trackway_03 1.1057530
#> Trackway_04 3.7306486
#> Trackway_07 1.1412773
#> Trackway_08 0.1487471
#> Trackway_09 1.0843279
#> Trackway_13 1.4773603
#> Trackway_15 8.5833312
#> Trackway_16 -1.0000000
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[76]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1.696326 4.682034 0.6554112 2.8752825
#> Trackway_02 1.6963262 NA 2.928205 2.3469843 1.9913562
#> Trackway_03 4.6820336 2.928205 NA 5.0458469 2.4514541
#> Trackway_04 0.6554112 2.346984 5.045847 NA 3.1972038
#> Trackway_07 2.8752825 1.991356 2.451454 3.1972038 NA
#> Trackway_08 3.3465032 2.152217 1.800467 3.7406400 0.6755159
#> Trackway_09 2.8896679 1.272261 1.689345 3.4539168 1.6800202
#> Trackway_13 4.3058847 2.616394 1.403365 4.9140162 3.0615413
#> Trackway_15 11.7297280 10.582069 8.063449 -1.0000000 -1.0000000
#> Trackway_16 6.0934984 5.666376 4.341025 6.1993687 3.6879839
#> Trackway_18 3.2886869 1.907587 1.412997 4.2475535 0.9988028
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.3465032 2.889668 4.305885 11.729728 6.093498
#> Trackway_02 2.1522173 1.272261 2.616394 10.582069 5.666376
#> Trackway_03 1.8004674 1.689345 1.403365 8.063449 4.341025
#> Trackway_04 3.7406400 3.453917 4.914016 -1.000000 6.199369
#> Trackway_07 0.6755159 1.680020 3.061541 -1.000000 3.687984
#> Trackway_08 NA 1.418296 2.551696 -1.000000 3.468186
#> Trackway_09 1.4182963 NA 1.578902 -1.000000 4.994801
#> Trackway_13 2.5516959 1.578902 NA -1.000000 5.695393
#> Trackway_15 -1.0000000 -1.000000 -1.000000 NA 6.139761
#> Trackway_16 3.4681858 4.994801 5.695393 6.139761 NA
#> Trackway_18 0.4695395 1.096701 2.098867 -1.000000 3.896561
#> Trackway_18
#> Trackway_01 3.2886869
#> Trackway_02 1.9075870
#> Trackway_03 1.4129972
#> Trackway_04 4.2475535
#> Trackway_07 0.9988028
#> Trackway_08 0.4695395
#> Trackway_09 1.0967006
#> Trackway_13 2.0988665
#> Trackway_15 -1.0000000
#> Trackway_16 3.8965611
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[77]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0.7594401 2.9387367 1.195164 2.4463530
#> Trackway_02 0.7594401 NA 2.3864175 1.873456 1.7105748
#> Trackway_03 2.9387367 2.3864175 NA 3.093198 1.3317862
#> Trackway_04 1.1951644 1.8734564 3.0931983 NA 3.0988627
#> Trackway_07 2.4463530 1.7105748 1.3317862 3.098863 NA
#> Trackway_08 3.1571237 2.4827734 0.7894987 3.609509 0.9204773
#> Trackway_09 2.6286260 2.2351064 0.4771023 2.676781 1.4414815
#> Trackway_13 1.9921095 1.3525418 1.1746724 2.649389 0.7105624
#> Trackway_15 11.5979969 -1.0000000 -1.0000000 -1.000000 9.2443089
#> Trackway_16 -1.0000000 6.6352943 -1.0000000 8.099027 5.0086278
#> Trackway_18 3.7021424 3.1701474 0.8014606 3.744238 1.9706960
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.1571237 2.6286260 1.9921095 11.597997 -1.000000
#> Trackway_02 2.4827734 2.2351064 1.3525418 -1.000000 6.635294
#> Trackway_03 0.7894987 0.4771023 1.1746724 -1.000000 -1.000000
#> Trackway_04 3.6095092 2.6767809 2.6493894 -1.000000 8.099027
#> Trackway_07 0.9204773 1.4414815 0.7105624 9.244309 5.008628
#> Trackway_08 NA 1.1609751 1.1687642 8.443512 4.639565
#> Trackway_09 1.1609751 NA 0.9738223 9.146531 5.767196
#> Trackway_13 1.1687642 0.9738223 NA 9.605894 5.646122
#> Trackway_15 8.4435121 9.1465309 9.6058944 NA -1.000000
#> Trackway_16 4.6395649 5.7671965 5.6461224 -1.000000 NA
#> Trackway_18 1.1560779 1.1331610 1.9745467 -1.000000 5.124526
#> Trackway_18
#> Trackway_01 3.7021424
#> Trackway_02 3.1701474
#> Trackway_03 0.8014606
#> Trackway_04 3.7442384
#> Trackway_07 1.9706960
#> Trackway_08 1.1560779
#> Trackway_09 1.1331610
#> Trackway_13 1.9745467
#> Trackway_15 -1.0000000
#> Trackway_16 5.1245256
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[78]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0.8315813 2.3412841 2.163436 2.1232711
#> Trackway_02 0.8315813 NA 2.1441343 2.672206 2.1182324
#> Trackway_03 2.3412841 2.1441343 NA 3.616888 1.6639566
#> Trackway_04 2.1634357 2.6722057 3.6168884 NA 2.2727296
#> Trackway_07 2.1232711 2.1182324 1.6639566 2.272730 NA
#> Trackway_08 3.3281189 3.4704409 2.2451601 3.128996 1.2737561
#> Trackway_09 1.5437635 1.3763398 1.1519652 2.465174 0.8882676
#> Trackway_13 1.2157037 0.9620179 1.3748670 2.342073 1.1629576
#> Trackway_15 -1.0000000 11.0385630 9.2220295 12.517065 10.2447418
#> Trackway_16 -1.0000000 -1.0000000 5.5578178 -1.000000 5.7364411
#> Trackway_18 2.5853257 2.1212805 0.2445554 3.830667 1.8075194
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.328119 1.5437635 1.2157037 -1.000000 -1.000000
#> Trackway_02 3.470441 1.3763398 0.9620179 11.038563 -1.000000
#> Trackway_03 2.245160 1.1519652 1.3748670 9.222030 5.557818
#> Trackway_04 3.128996 2.4651743 2.3420734 12.517065 -1.000000
#> Trackway_07 1.273756 0.8882676 1.1629576 10.244742 5.736441
#> Trackway_08 NA 1.9073301 2.3167160 9.575809 4.685709
#> Trackway_09 1.907330 NA 0.4328305 -1.000000 6.119142
#> Trackway_13 2.316716 0.4328305 NA 10.556923 6.539909
#> Trackway_15 9.575809 -1.0000000 10.5569233 NA 5.786055
#> Trackway_16 4.685709 6.1191421 6.5399093 5.786055 NA
#> Trackway_18 2.539487 1.4525736 1.6006682 8.977543 -1.000000
#> Trackway_18
#> Trackway_01 2.5853257
#> Trackway_02 2.1212805
#> Trackway_03 0.2445554
#> Trackway_04 3.8306672
#> Trackway_07 1.8075194
#> Trackway_08 2.5394868
#> Trackway_09 1.4525736
#> Trackway_13 1.6006682
#> Trackway_15 8.9775433
#> Trackway_16 -1.0000000
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[79]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1.885907 3.3264698 0.9977854 2.6096340
#> Trackway_02 1.8859069 NA 2.0751315 1.6254956 2.2415444
#> Trackway_03 3.3264698 2.075131 NA 3.4623892 1.1100902
#> Trackway_04 0.9977854 1.625496 3.4623892 NA 3.1158308
#> Trackway_07 2.6096340 2.241544 1.1100902 3.1158308 NA
#> Trackway_08 3.1648259 2.958317 1.7112011 3.7744072 0.8284159
#> Trackway_09 2.7001774 1.712822 0.5515581 3.0658949 0.7889943
#> Trackway_13 1.8544262 1.465278 1.4164393 2.4693196 1.0502846
#> Trackway_15 -1.0000000 10.968307 8.9094150 12.3321582 9.2941335
#> Trackway_16 6.9580760 6.888659 -1.0000000 7.6721846 4.7044427
#> Trackway_18 3.2619604 2.345972 0.8078937 3.6100866 1.0278273
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.1648259 2.7001774 1.8544262 -1.000000 6.958076
#> Trackway_02 2.9583167 1.7128217 1.4652777 10.968307 6.888659
#> Trackway_03 1.7112011 0.5515581 1.4164393 8.909415 -1.000000
#> Trackway_04 3.7744072 3.0658949 2.4693196 12.332158 7.672185
#> Trackway_07 0.8284159 0.7889943 1.0502846 9.294133 4.704443
#> Trackway_08 NA 1.4649474 1.5536729 8.812139 3.957436
#> Trackway_09 1.4649474 NA 0.9176669 9.353146 5.241772
#> Trackway_13 1.5536729 0.9176669 NA -1.000000 5.510967
#> Trackway_15 8.8121393 9.3531461 -1.0000000 NA -1.000000
#> Trackway_16 3.9574355 5.2417719 5.5109672 -1.000000 NA
#> Trackway_18 1.2031992 0.6414803 2.1273205 8.722727 4.692130
#> Trackway_18
#> Trackway_01 3.2619604
#> Trackway_02 2.3459716
#> Trackway_03 0.8078937
#> Trackway_04 3.6100866
#> Trackway_07 1.0278273
#> Trackway_08 1.2031992
#> Trackway_09 0.6414803
#> Trackway_13 2.1273205
#> Trackway_15 8.7227275
#> Trackway_16 4.6921295
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[80]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1.952110 4.1335915 0.8112265 2.3532687
#> Trackway_02 1.9521095 NA 2.5703329 2.4286193 2.3606988
#> Trackway_03 4.1335915 2.570333 NA 4.6040280 2.1278626
#> Trackway_04 0.8112265 2.428619 4.6040280 NA 3.0610588
#> Trackway_07 2.3532687 2.360699 2.1278626 3.0610588 NA
#> Trackway_08 3.6147395 2.755277 0.7911526 4.3446787 1.5546303
#> Trackway_09 3.4177454 2.120225 0.4504862 4.2514612 1.9222969
#> Trackway_13 2.1824149 1.443556 1.6942451 2.8516098 1.0992789
#> Trackway_15 11.9480761 11.324999 8.8303886 12.6507987 9.5948080
#> Trackway_16 7.1541243 -1.000000 -1.0000000 7.7537125 5.0112136
#> Trackway_18 2.9755048 2.516240 1.5281927 3.7469397 0.7563741
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.6147395 3.4177454 2.182415 11.948076 7.154124
#> Trackway_02 2.7552767 2.1202252 1.443556 11.324999 -1.000000
#> Trackway_03 0.7911526 0.4504862 1.694245 8.830389 -1.000000
#> Trackway_04 4.3446787 4.2514612 2.851610 12.650799 7.753713
#> Trackway_07 1.5546303 1.9222969 1.099279 9.594808 5.011214
#> Trackway_08 NA 0.9302191 1.557702 8.580166 -1.000000
#> Trackway_09 0.9302191 NA 1.306433 9.259965 5.779099
#> Trackway_13 1.5577025 1.3064327 NA 10.110360 -1.000000
#> Trackway_15 8.5801663 9.2599652 10.110360 NA 5.787833
#> Trackway_16 -1.0000000 5.7790993 -1.000000 5.787833 NA
#> Trackway_18 0.9559890 1.3700904 1.168807 -1.000000 -1.000000
#> Trackway_18
#> Trackway_01 2.9755048
#> Trackway_02 2.5162401
#> Trackway_03 1.5281927
#> Trackway_04 3.7469397
#> Trackway_07 0.7563741
#> Trackway_08 0.9559890
#> Trackway_09 1.3700904
#> Trackway_13 1.1688069
#> Trackway_15 -1.0000000
#> Trackway_16 -1.0000000
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[81]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 4.379574 5.2814531 4.046053 2.7166049
#> Trackway_02 4.379574 NA 2.4632135 1.473796 2.7079169
#> Trackway_03 5.281453 2.463214 NA 3.908385 2.6048854
#> Trackway_04 4.046053 1.473796 3.9083852 NA 3.2882343
#> Trackway_07 2.716605 2.707917 2.6048854 3.288234 NA
#> Trackway_08 3.011158 3.116719 2.5947733 3.911626 0.8050401
#> Trackway_09 3.063072 1.746979 3.0111838 2.219831 1.2485078
#> Trackway_13 3.484841 1.451993 2.0923388 2.578288 1.3369343
#> Trackway_15 -1.000000 10.527546 -1.0000000 11.945734 -1.0000000
#> Trackway_16 6.657367 -1.000000 -1.0000000 8.290642 -1.0000000
#> Trackway_18 4.892614 2.282980 0.8848018 3.614061 2.3393478
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.0111576 3.0630716 3.4848413 -1.000000 6.657367
#> Trackway_02 3.1167188 1.7469793 1.4519925 10.527546 -1.000000
#> Trackway_03 2.5947733 3.0111838 2.0923388 -1.000000 -1.000000
#> Trackway_04 3.9116265 2.2198314 2.5782875 11.945734 8.290642
#> Trackway_07 0.8050401 1.2485078 1.3369343 -1.000000 -1.000000
#> Trackway_08 NA 1.7047437 2.0242305 -1.000000 4.452856
#> Trackway_09 1.7047437 NA 0.7136273 -1.000000 -1.000000
#> Trackway_13 2.0242305 0.7136273 NA -1.000000 5.903201
#> Trackway_15 -1.0000000 -1.0000000 -1.0000000 NA -1.000000
#> Trackway_16 4.4528558 -1.0000000 5.9032013 -1.000000 NA
#> Trackway_18 2.2647765 2.3426878 1.6412654 8.334329 -1.000000
#> Trackway_18
#> Trackway_01 4.8926136
#> Trackway_02 2.2829797
#> Trackway_03 0.8848018
#> Trackway_04 3.6140607
#> Trackway_07 2.3393478
#> Trackway_08 2.2647765
#> Trackway_09 2.3426878
#> Trackway_13 1.6412654
#> Trackway_15 8.3343288
#> Trackway_16 -1.0000000
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[82]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1.6020397 4.8622724 1.8290812 2.3887565
#> Trackway_02 1.602040 NA 3.2550815 0.8171097 1.7318725
#> Trackway_03 4.862272 3.2550815 NA 4.4503679 2.3630453
#> Trackway_04 1.829081 0.8171097 4.4503679 NA 2.5855468
#> Trackway_07 2.388757 1.7318725 2.3630453 2.5855468 NA
#> Trackway_08 2.831047 2.5524052 2.6953090 3.3790703 0.8835764
#> Trackway_09 2.675954 1.9249444 2.1001098 2.7323086 0.3935160
#> Trackway_13 3.986503 2.5766934 0.9223978 3.0304403 2.2073735
#> Trackway_15 12.015417 11.2878822 8.3805215 -1.0000000 9.7037331
#> Trackway_16 7.109490 7.0488507 5.5765338 7.8654893 -1.0000000
#> Trackway_18 3.678428 2.6396744 1.1033202 3.3771383 1.3426047
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 2.8310470 2.6759536 3.9865028 12.015417 7.109490
#> Trackway_02 2.5524052 1.9249444 2.5766934 11.287882 7.048851
#> Trackway_03 2.6953090 2.1001098 0.9223978 8.380522 5.576534
#> Trackway_04 3.3790703 2.7323086 3.0304403 -1.000000 7.865489
#> Trackway_07 0.8835764 0.3935160 2.2073735 9.703733 -1.000000
#> Trackway_08 NA 0.8740513 2.7453480 -1.000000 -1.000000
#> Trackway_09 0.8740513 NA 2.1298251 -1.000000 5.187513
#> Trackway_13 2.7453480 2.1298251 NA 9.302284 6.276045
#> Trackway_15 -1.0000000 -1.0000000 9.3022840 NA -1.000000
#> Trackway_16 -1.0000000 5.1875134 6.2760447 -1.000000 NA
#> Trackway_18 1.5932827 1.0575491 1.9816945 8.660067 5.028018
#> Trackway_18
#> Trackway_01 3.678428
#> Trackway_02 2.639674
#> Trackway_03 1.103320
#> Trackway_04 3.377138
#> Trackway_07 1.342605
#> Trackway_08 1.593283
#> Trackway_09 1.057549
#> Trackway_13 1.981695
#> Trackway_15 8.660067
#> Trackway_16 5.028018
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[83]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1.057220 3.2828610 1.352112 2.422988
#> Trackway_02 1.057220 NA 2.3129782 2.206193 2.060552
#> Trackway_03 3.282861 2.312978 NA 4.011486 2.107409
#> Trackway_04 1.352112 2.206193 4.0114857 NA 2.445326
#> Trackway_07 2.422988 2.060552 2.1074092 2.445326 NA
#> Trackway_08 2.920844 2.293701 1.2587638 3.276121 0.888053
#> Trackway_09 3.018532 2.243721 0.6019364 3.695174 1.546047
#> Trackway_13 2.146711 1.186710 1.1750538 3.047433 1.753438
#> Trackway_15 11.665357 10.778237 -1.0000000 -1.000000 9.552401
#> Trackway_16 7.748777 7.174002 5.3698073 7.601319 5.334170
#> Trackway_18 3.636887 2.638872 0.5937990 4.084406 1.868360
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 2.9208444 3.0185315 2.146711 11.665357 7.748777
#> Trackway_02 2.2937009 2.2437214 1.186710 10.778237 7.174002
#> Trackway_03 1.2587638 0.6019364 1.175054 -1.000000 5.369807
#> Trackway_04 3.2761209 3.6951735 3.047433 -1.000000 7.601319
#> Trackway_07 0.8880530 1.5460466 1.753438 9.552401 5.334170
#> Trackway_08 NA 0.7659767 2.101742 8.807742 4.928238
#> Trackway_09 0.7659767 NA 1.187851 8.658523 -1.000000
#> Trackway_13 2.1017418 1.1878507 NA -1.000000 6.278276
#> Trackway_15 8.8077417 8.6585233 -1.000000 NA 5.371102
#> Trackway_16 4.9282381 -1.0000000 6.278276 5.371102 NA
#> Trackway_18 0.9892651 0.5099886 1.550227 8.148610 -1.000000
#> Trackway_18
#> Trackway_01 3.6368871
#> Trackway_02 2.6388719
#> Trackway_03 0.5937990
#> Trackway_04 4.0844057
#> Trackway_07 1.8683598
#> Trackway_08 0.9892651
#> Trackway_09 0.5099886
#> Trackway_13 1.5502273
#> Trackway_15 8.1486104
#> Trackway_16 -1.0000000
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[84]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0.5151988 2.7628473 1.433831 2.3837186
#> Trackway_02 0.5151988 NA 2.4319876 1.618847 2.0338909
#> Trackway_03 2.7628473 2.4319876 NA 3.112144 1.8770939
#> Trackway_04 1.4338311 1.6188471 3.1121436 NA 3.5991467
#> Trackway_07 2.3837186 2.0338909 1.8770939 3.599147 NA
#> Trackway_08 3.1905824 2.6630911 2.1200450 4.176391 0.8074572
#> Trackway_09 2.8484574 2.5902771 0.6565370 2.973338 2.3645742
#> Trackway_13 2.4858500 2.2838993 0.8891333 2.508215 2.5686399
#> Trackway_15 -1.0000000 -1.0000000 8.7864705 -1.000000 9.9267430
#> Trackway_16 -1.0000000 7.3756440 5.4451702 -1.000000 5.5918717
#> Trackway_18 2.6828505 2.2972030 0.9155898 3.216682 1.6775341
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.1905824 2.8484574 2.4858500 -1.000000 -1.000000
#> Trackway_02 2.6630911 2.5902771 2.2838993 -1.000000 7.375644
#> Trackway_03 2.1200450 0.6565370 0.8891333 8.786470 5.445170
#> Trackway_04 4.1763906 2.9733377 2.5082148 -1.000000 -1.000000
#> Trackway_07 0.8074572 2.3645742 2.5686399 9.926743 5.591872
#> Trackway_08 NA 2.3971404 2.6413539 9.211618 -1.000000
#> Trackway_09 2.3971404 NA 0.4799576 -1.000000 -1.000000
#> Trackway_13 2.6413539 0.4799576 NA -1.000000 -1.000000
#> Trackway_15 9.2116181 -1.0000000 -1.0000000 NA 5.611011
#> Trackway_16 -1.0000000 -1.0000000 -1.0000000 5.611011 NA
#> Trackway_18 1.4028489 1.0604296 1.2346163 -1.000000 -1.000000
#> Trackway_18
#> Trackway_01 2.6828505
#> Trackway_02 2.2972030
#> Trackway_03 0.9155898
#> Trackway_04 3.2166818
#> Trackway_07 1.6775341
#> Trackway_08 1.4028489
#> Trackway_09 1.0604296
#> Trackway_13 1.2346163
#> Trackway_15 -1.0000000
#> Trackway_16 -1.0000000
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[85]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0.9798126 3.612856 0.5081726 2.3884854
#> Trackway_02 0.9798126 NA 2.618562 1.2609491 2.1710504
#> Trackway_03 3.6128556 2.6185625 NA 3.8576365 2.3772712
#> Trackway_04 0.5081726 1.2609491 3.857637 NA 2.8687485
#> Trackway_07 2.3884854 2.1710504 2.377271 2.8687485 NA
#> Trackway_08 3.0008079 2.6380984 2.093387 3.4666373 0.6752437
#> Trackway_09 2.7501186 1.6814416 1.132213 2.9348486 2.2014599
#> Trackway_13 1.9130052 1.2590550 1.691921 2.3351900 1.1908626
#> Trackway_15 11.3942404 -1.0000000 8.316147 -1.0000000 -1.0000000
#> Trackway_16 7.7943677 -1.0000000 5.724560 8.2616421 5.4059125
#> Trackway_18 2.9302849 2.3998868 1.172709 3.4128961 1.3955836
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.0008079 2.750119 1.913005 11.394240 7.794368
#> Trackway_02 2.6380984 1.681442 1.259055 -1.000000 -1.000000
#> Trackway_03 2.0933870 1.132213 1.691921 8.316147 5.724560
#> Trackway_04 3.4666373 2.934849 2.335190 -1.000000 8.261642
#> Trackway_07 0.6752437 2.201460 1.190863 -1.000000 5.405913
#> Trackway_08 NA 2.128237 1.891264 -1.000000 4.818940
#> Trackway_09 2.1282367 NA 1.057617 -1.000000 -1.000000
#> Trackway_13 1.8912643 1.057617 NA -1.000000 6.194350
#> Trackway_15 -1.0000000 -1.000000 -1.000000 NA 4.738101
#> Trackway_16 4.8189395 -1.000000 6.194350 4.738101 NA
#> Trackway_18 0.9370146 1.275088 1.039516 8.480871 -1.000000
#> Trackway_18
#> Trackway_01 2.9302849
#> Trackway_02 2.3998868
#> Trackway_03 1.1727092
#> Trackway_04 3.4128961
#> Trackway_07 1.3955836
#> Trackway_08 0.9370146
#> Trackway_09 1.2750876
#> Trackway_13 1.0395160
#> Trackway_15 8.4808710
#> Trackway_16 -1.0000000
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[86]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 2.4419216 3.7315756 2.0448060 2.7007527
#> Trackway_02 2.441922 NA 2.4140750 0.9680683 2.3807422
#> Trackway_03 3.731576 2.4140750 NA 3.4575213 1.3953636
#> Trackway_04 2.044806 0.9680683 3.4575213 NA 2.9387983
#> Trackway_07 2.700753 2.3807422 1.3953636 2.9387983 NA
#> Trackway_08 3.186326 2.5627042 0.8590472 3.2278418 0.8690957
#> Trackway_09 4.256718 2.4236193 0.9078350 3.5426654 2.2500223
#> Trackway_13 2.220092 1.2700484 2.0574274 1.9406065 1.0352068
#> Trackway_15 11.794370 -1.0000000 8.4688073 -1.0000000 9.1850110
#> Trackway_16 -1.000000 7.6635126 5.4569678 8.3800421 -1.0000000
#> Trackway_18 3.067075 2.7375377 1.5510088 3.3408632 0.4420138
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.1863260 4.256718 2.220092 11.794370 -1.000000
#> Trackway_02 2.5627042 2.423619 1.270048 -1.000000 7.663513
#> Trackway_03 0.8590472 0.907835 2.057427 8.468807 5.456968
#> Trackway_04 3.2278418 3.542665 1.940606 -1.000000 8.380042
#> Trackway_07 0.8690957 2.250022 1.035207 9.185011 -1.000000
#> Trackway_08 NA 1.710781 1.292486 8.707737 5.202689
#> Trackway_09 1.7107815 NA 2.040373 8.555040 -1.000000
#> Trackway_13 1.2924859 2.040373 NA 9.954357 6.450254
#> Trackway_15 8.7077374 8.555040 9.954357 NA 5.212209
#> Trackway_16 5.2026891 -1.000000 6.450254 5.212209 NA
#> Trackway_18 0.9677384 2.436865 1.468168 8.958482 -1.000000
#> Trackway_18
#> Trackway_01 3.0670754
#> Trackway_02 2.7375377
#> Trackway_03 1.5510088
#> Trackway_04 3.3408632
#> Trackway_07 0.4420138
#> Trackway_08 0.9677384
#> Trackway_09 2.4368655
#> Trackway_13 1.4681682
#> Trackway_15 8.9584823
#> Trackway_16 -1.0000000
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[87]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1.650185 2.5165000 1.533819 2.4698804
#> Trackway_02 1.650185 NA 2.4425106 1.774922 2.1162263
#> Trackway_03 2.516500 2.442511 NA 3.342427 1.0428700
#> Trackway_04 1.533819 1.774922 3.3424269 NA 3.1510479
#> Trackway_07 2.469880 2.116226 1.0428700 3.151048 NA
#> Trackway_08 2.802404 2.509065 0.9103700 3.656182 0.7305789
#> Trackway_09 2.340995 2.505027 0.5377354 3.392800 1.1554360
#> Trackway_13 1.978899 2.472699 1.2441130 3.282290 2.0605047
#> Trackway_15 -1.000000 11.289382 8.9984647 12.340393 9.4368387
#> Trackway_16 7.549299 -1.000000 5.0577883 -1.000000 -1.0000000
#> Trackway_18 2.861227 3.060497 1.0054073 4.008768 1.6836851
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 2.8024039 2.3409949 1.9788989 -1.000000 7.549299
#> Trackway_02 2.5090655 2.5050267 2.4726987 11.289382 -1.000000
#> Trackway_03 0.9103700 0.5377354 1.2441130 8.998465 5.057788
#> Trackway_04 3.6561816 3.3928002 3.2822901 12.340393 -1.000000
#> Trackway_07 0.7305789 1.1554360 2.0605047 9.436839 -1.000000
#> Trackway_08 NA 0.8161850 1.5441173 -1.000000 4.755303
#> Trackway_09 0.8161850 NA 0.7352635 8.996163 -1.000000
#> Trackway_13 1.5441173 0.7352635 NA 9.344436 6.054023
#> Trackway_15 -1.0000000 8.9961631 9.3444357 NA -1.000000
#> Trackway_16 4.7553028 -1.0000000 6.0540228 -1.000000 NA
#> Trackway_18 1.1477957 0.6397821 0.9556272 -1.000000 5.161831
#> Trackway_18
#> Trackway_01 2.8612267
#> Trackway_02 3.0604967
#> Trackway_03 1.0054073
#> Trackway_04 4.0087675
#> Trackway_07 1.6836851
#> Trackway_08 1.1477957
#> Trackway_09 0.6397821
#> Trackway_13 0.9556272
#> Trackway_15 -1.0000000
#> Trackway_16 5.1618306
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[88]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1.322198 3.5917029 1.326919 2.642521
#> Trackway_02 1.322198 NA 2.5752615 2.595531 2.278829
#> Trackway_03 3.591703 2.575262 NA 4.731213 1.306528
#> Trackway_04 1.326919 2.595531 4.7312131 NA 3.626456
#> Trackway_07 2.642521 2.278829 1.3065282 3.626456 NA
#> Trackway_08 4.371392 3.349029 0.7830801 5.494869 1.962504
#> Trackway_09 4.116271 3.178449 0.5628997 5.277110 1.859578
#> Trackway_13 2.492900 1.529749 1.0999505 3.653373 0.804605
#> Trackway_15 11.940768 11.298902 8.8431377 12.688744 9.339536
#> Trackway_16 7.245930 7.075333 5.3437822 7.660754 5.072422
#> Trackway_18 3.410912 2.570768 0.9212745 4.477561 1.013423
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 4.3713925 4.1162707 2.492900 11.940768 7.245930
#> Trackway_02 3.3490293 3.1784489 1.529749 11.298902 7.075333
#> Trackway_03 0.7830801 0.5628997 1.099950 8.843138 5.343782
#> Trackway_04 5.4948687 5.2771102 3.653373 12.688744 7.660754
#> Trackway_07 1.9625040 1.8595778 0.804605 9.339536 5.072422
#> Trackway_08 NA 0.3962005 1.918756 8.174190 5.094257
#> Trackway_09 0.3962005 NA 1.627535 -1.000000 5.432646
#> Trackway_13 1.9187557 1.6275346 NA 9.777469 5.794383
#> Trackway_15 8.1741903 -1.0000000 9.777469 NA -1.000000
#> Trackway_16 5.0942569 5.4326458 5.794383 -1.000000 NA
#> Trackway_18 1.0631783 1.0003831 1.020854 -1.000000 4.971876
#> Trackway_18
#> Trackway_01 3.4109115
#> Trackway_02 2.5707679
#> Trackway_03 0.9212745
#> Trackway_04 4.4775613
#> Trackway_07 1.0134232
#> Trackway_08 1.0631783
#> Trackway_09 1.0003831
#> Trackway_13 1.0208541
#> Trackway_15 -1.0000000
#> Trackway_16 4.9718763
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[89]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1.713296 3.1301046 1.714870 3.0301023
#> Trackway_02 1.713296 NA 3.1941667 1.029149 2.2407243
#> Trackway_03 3.130105 3.194167 NA 4.549124 1.5696996
#> Trackway_04 1.714870 1.029149 4.5491242 NA 3.2595876
#> Trackway_07 3.030102 2.240724 1.5696996 3.259588 NA
#> Trackway_08 3.217125 2.252523 1.8842613 3.278486 0.8490392
#> Trackway_09 2.267502 2.191229 1.0732791 3.032931 1.3116073
#> Trackway_13 1.392532 1.458100 1.9045021 2.222123 1.9160964
#> Trackway_15 -1.000000 11.215086 8.1606158 12.180402 9.0407295
#> Trackway_16 8.194061 7.450543 -1.0000000 8.475599 5.2655848
#> Trackway_18 2.810243 2.759293 0.5333515 3.613430 1.1150991
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.2171254 2.2675022 1.3925317 -1.000000 8.194061
#> Trackway_02 2.2525227 2.1912288 1.4580999 11.215086 7.450543
#> Trackway_03 1.8842613 1.0732791 1.9045021 8.160616 -1.000000
#> Trackway_04 3.2784858 3.0329307 2.2221232 12.180402 8.475599
#> Trackway_07 0.8490392 1.3116073 1.9160964 9.040730 5.265585
#> Trackway_08 NA 1.7045515 1.8862804 9.147737 5.200538
#> Trackway_09 1.7045515 NA 0.8312848 9.230864 6.115032
#> Trackway_13 1.8862804 0.8312848 NA -1.000000 6.805446
#> Trackway_15 9.1477370 9.2308643 -1.0000000 NA -1.000000
#> Trackway_16 5.2005381 6.1150318 6.8054458 -1.000000 NA
#> Trackway_18 1.4434281 0.7949696 1.4936362 -1.000000 -1.000000
#> Trackway_18
#> Trackway_01 2.8102432
#> Trackway_02 2.7592930
#> Trackway_03 0.5333515
#> Trackway_04 3.6134298
#> Trackway_07 1.1150991
#> Trackway_08 1.4434281
#> Trackway_09 0.7949696
#> Trackway_13 1.4936362
#> Trackway_15 -1.0000000
#> Trackway_16 -1.0000000
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[90]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 2.0917087 4.2942855 1.390168 3.0531822
#> Trackway_02 2.091709 NA 2.2016851 1.549964 1.7504711
#> Trackway_03 4.294286 2.2016851 NA 3.751390 1.4980494
#> Trackway_04 1.390168 1.5499644 3.7513897 NA 3.0891917
#> Trackway_07 3.053182 1.7504711 1.4980494 3.089192 NA
#> Trackway_08 3.664459 2.1215902 0.7838503 3.664048 0.8203733
#> Trackway_09 3.285281 1.7132992 1.1302905 2.744252 1.5941105
#> Trackway_13 2.304633 0.8092521 1.7511042 2.194408 0.9452611
#> Trackway_15 -1.000000 -1.0000000 8.5113534 12.160269 -1.0000000
#> Trackway_16 -1.000000 7.4246688 5.8220301 -1.000000 5.6850170
#> Trackway_18 3.953838 2.2935855 0.5153208 3.824656 1.1622438
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.6644588 3.285281 2.3046329 -1.000000 -1.000000
#> Trackway_02 2.1215902 1.713299 0.8092521 -1.000000 7.424669
#> Trackway_03 0.7838503 1.130291 1.7511042 8.511353 5.822030
#> Trackway_04 3.6640483 2.744252 2.1944083 12.160269 -1.000000
#> Trackway_07 0.8203733 1.594111 0.9452611 -1.000000 5.685017
#> Trackway_08 NA 1.526372 1.4394848 -1.000000 5.421318
#> Trackway_09 1.5263720 NA 1.3577631 -1.000000 -1.000000
#> Trackway_13 1.4394848 1.357763 NA 9.975511 6.628599
#> Trackway_15 -1.0000000 -1.000000 9.9755114 NA -1.000000
#> Trackway_16 5.4213185 -1.000000 6.6285988 -1.000000 NA
#> Trackway_18 0.8978743 1.405812 1.6837319 8.345816 5.413551
#> Trackway_18
#> Trackway_01 3.9538379
#> Trackway_02 2.2935855
#> Trackway_03 0.5153208
#> Trackway_04 3.8246560
#> Trackway_07 1.1622438
#> Trackway_08 0.8978743
#> Trackway_09 1.4058119
#> Trackway_13 1.6837319
#> Trackway_15 8.3458160
#> Trackway_16 5.4135514
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[91]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 2.831680 4.2726782 1.211444 3.4863498
#> Trackway_02 2.831680 NA 2.6319507 2.433527 2.2117834
#> Trackway_03 4.272678 2.631951 NA 4.453472 0.9239472
#> Trackway_04 1.211444 2.433527 4.4534722 NA 3.5895659
#> Trackway_07 3.486350 2.211783 0.9239472 3.589566 NA
#> Trackway_08 3.771516 2.820528 0.8406307 4.155461 0.6872321
#> Trackway_09 4.509224 2.627888 0.3731090 4.606730 1.3076081
#> Trackway_13 3.501695 1.437588 1.1790253 3.451086 0.8556166
#> Trackway_15 11.697474 11.126681 -1.0000000 12.430597 -1.0000000
#> Trackway_16 -1.000000 -1.000000 5.6671593 -1.000000 5.7057640
#> Trackway_18 3.940573 2.756782 0.6704396 4.290133 0.7525365
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.7715160 4.509224 3.5016945 11.697474 -1.000000
#> Trackway_02 2.8205284 2.627888 1.4375881 11.126681 -1.000000
#> Trackway_03 0.8406307 0.373109 1.1790253 -1.000000 5.667159
#> Trackway_04 4.1554611 4.606730 3.4510865 12.430597 -1.000000
#> Trackway_07 0.6872321 1.307608 0.8556166 -1.000000 5.705764
#> Trackway_08 NA 1.213162 1.4670378 8.450802 5.075841
#> Trackway_09 1.2131618 NA 1.2024898 8.664743 5.964219
#> Trackway_13 1.4670378 1.202490 NA 9.730796 -1.000000
#> Trackway_15 8.4508023 8.664743 9.7307962 NA -1.000000
#> Trackway_16 5.0758413 5.964219 -1.0000000 -1.000000 NA
#> Trackway_18 0.1970654 1.193120 1.4464053 8.379807 -1.000000
#> Trackway_18
#> Trackway_01 3.9405733
#> Trackway_02 2.7567817
#> Trackway_03 0.6704396
#> Trackway_04 4.2901331
#> Trackway_07 0.7525365
#> Trackway_08 0.1970654
#> Trackway_09 1.1931201
#> Trackway_13 1.4464053
#> Trackway_15 8.3798069
#> Trackway_16 -1.0000000
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[92]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1.441136 4.5366686 3.781981 3.2246818
#> Trackway_02 1.441136 NA 3.2502697 2.503155 2.2812939
#> Trackway_03 4.536669 3.250270 NA 4.004223 1.5244152
#> Trackway_04 3.781981 2.503155 4.0042226 NA 3.8071444
#> Trackway_07 3.224682 2.281294 1.5244152 3.807144 NA
#> Trackway_08 3.677429 2.708423 1.1917704 4.017562 0.4538425
#> Trackway_09 3.608893 2.231570 1.0215531 3.011738 1.0386242
#> Trackway_13 3.579247 1.992610 2.1191634 2.433822 1.5199843
#> Trackway_15 11.329089 -1.000000 7.8064868 11.555566 -1.0000000
#> Trackway_16 -1.000000 7.307137 -1.0000000 9.053042 5.2659793
#> Trackway_18 4.054131 2.996678 0.7354275 3.900515 0.9344309
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.6774288 3.6088928 3.5792475 11.329089 -1.000000
#> Trackway_02 2.7084232 2.2315697 1.9926098 -1.000000 7.307137
#> Trackway_03 1.1917704 1.0215531 2.1191634 7.806487 -1.000000
#> Trackway_04 4.0175621 3.0117382 2.4338223 11.555566 9.053042
#> Trackway_07 0.4538425 1.0386242 1.5199843 -1.000000 5.265979
#> Trackway_08 NA 1.1922740 1.6112024 -1.000000 5.047568
#> Trackway_09 1.1922740 NA 0.6170003 8.681279 -1.000000
#> Trackway_13 1.6112024 0.6170003 NA -1.000000 -1.000000
#> Trackway_15 -1.0000000 8.6812793 -1.0000000 NA 4.610199
#> Trackway_16 5.0475676 -1.0000000 -1.0000000 4.610199 NA
#> Trackway_18 0.5673626 0.8663450 1.4326212 -1.000000 5.280749
#> Trackway_18
#> Trackway_01 4.0541306
#> Trackway_02 2.9966783
#> Trackway_03 0.7354275
#> Trackway_04 3.9005148
#> Trackway_07 0.9344309
#> Trackway_08 0.5673626
#> Trackway_09 0.8663450
#> Trackway_13 1.4326212
#> Trackway_15 -1.0000000
#> Trackway_16 5.2807485
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[93]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1.545802 2.7860867 1.124465 2.1711834
#> Trackway_02 1.545802 NA 1.9978626 1.279510 2.2151725
#> Trackway_03 2.786087 1.997863 NA 3.159244 1.2869516
#> Trackway_04 1.124465 1.279510 3.1592438 NA 3.0052508
#> Trackway_07 2.171183 2.215172 1.2869516 3.005251 NA
#> Trackway_08 3.117734 2.606643 0.5538656 3.597411 1.2127194
#> Trackway_09 2.688414 1.708555 0.3956890 3.039262 1.5673077
#> Trackway_13 1.543409 1.737111 1.5143845 2.348209 0.6327012
#> Trackway_15 11.094902 -1.000000 8.3189955 11.401950 9.1236823
#> Trackway_16 7.942992 -1.000000 5.6590690 -1.000000 5.7738635
#> Trackway_18 2.899999 2.339249 0.4219858 3.568892 1.0827134
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.1177339 2.6884136 1.5434093 11.094902 7.942992
#> Trackway_02 2.6066426 1.7085549 1.7371113 -1.000000 -1.000000
#> Trackway_03 0.5538656 0.3956890 1.5143845 8.318995 5.659069
#> Trackway_04 3.5974105 3.0392622 2.3482090 11.401950 -1.000000
#> Trackway_07 1.2127194 1.5673077 0.6327012 9.123682 5.773863
#> Trackway_08 NA 0.9456253 1.7990984 8.018216 5.137852
#> Trackway_09 0.9456253 NA 1.6067605 8.487216 6.007016
#> Trackway_13 1.7990984 1.6067605 NA 9.657432 6.405729
#> Trackway_15 8.0182158 8.4872163 9.6574324 NA -1.000000
#> Trackway_16 5.1378524 6.0070165 6.4057290 -1.000000 NA
#> Trackway_18 0.7917317 0.8162579 1.4773533 8.204255 5.324041
#> Trackway_18
#> Trackway_01 2.8999992
#> Trackway_02 2.3392492
#> Trackway_03 0.4219858
#> Trackway_04 3.5688919
#> Trackway_07 1.0827134
#> Trackway_08 0.7917317
#> Trackway_09 0.8162579
#> Trackway_13 1.4773533
#> Trackway_15 8.2042548
#> Trackway_16 5.3240413
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[94]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1.007393 3.7085314 1.407489 2.9987061
#> Trackway_02 1.007393 NA 2.9579433 1.903141 1.8859810
#> Trackway_03 3.708531 2.957943 NA 3.564685 1.6430588
#> Trackway_04 1.407489 1.903141 3.5646847 NA 3.1269264
#> Trackway_07 2.998706 1.885981 1.6430588 3.126926 NA
#> Trackway_08 3.257210 2.429957 1.4863200 3.668177 0.5308567
#> Trackway_09 2.457177 1.556531 1.4956926 2.765458 0.3620309
#> Trackway_13 3.027260 2.485611 1.0052628 2.648389 1.5901207
#> Trackway_15 -1.000000 10.381357 7.9979608 -1.000000 8.5624060
#> Trackway_16 7.690367 6.691986 5.6137855 8.365789 5.2879676
#> Trackway_18 3.977501 2.808984 0.6470931 3.784080 1.0104641
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.2572102 2.4571766 3.027260 -1.000000 7.690367
#> Trackway_02 2.4299571 1.5565310 2.485611 10.381357 6.691986
#> Trackway_03 1.4863200 1.4956926 1.005263 7.997961 5.613785
#> Trackway_04 3.6681768 2.7654580 2.648389 -1.000000 8.365789
#> Trackway_07 0.5308567 0.3620309 1.590121 8.562406 5.287968
#> Trackway_08 NA 0.8901865 1.963411 -1.000000 -1.000000
#> Trackway_09 0.8901865 NA 1.448707 8.906051 5.637148
#> Trackway_13 1.9634113 1.4487067 NA 8.987463 6.509707
#> Trackway_15 -1.0000000 8.9060514 8.987463 NA 5.165379
#> Trackway_16 -1.0000000 5.6371480 6.509707 5.165379 NA
#> Trackway_18 1.0207458 1.3089878 1.465182 7.771280 5.047607
#> Trackway_18
#> Trackway_01 3.9775014
#> Trackway_02 2.8089838
#> Trackway_03 0.6470931
#> Trackway_04 3.7840795
#> Trackway_07 1.0104641
#> Trackway_08 1.0207458
#> Trackway_09 1.3089878
#> Trackway_13 1.4651819
#> Trackway_15 7.7712799
#> Trackway_16 5.0476074
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[95]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 3.3692068 4.2420306 5.283153 2.8003409
#> Trackway_02 3.369207 NA 1.6546691 2.109545 1.9652896
#> Trackway_03 4.242031 1.6546691 NA 2.920494 1.6709527
#> Trackway_04 5.283153 2.1095446 2.9204941 NA 3.9740421
#> Trackway_07 2.800341 1.9652896 1.6709527 3.974042 NA
#> Trackway_08 3.664958 1.9906179 0.9838750 3.710978 0.8804758
#> Trackway_09 3.202673 1.4098052 1.1436289 3.364377 0.8238755
#> Trackway_13 3.590222 0.7174954 0.9502979 2.543709 1.5483503
#> Trackway_15 11.765494 -1.0000000 8.5973547 10.921039 9.1878512
#> Trackway_16 7.295397 -1.0000000 5.5176150 8.414166 5.2420616
#> Trackway_18 4.669784 2.1724744 0.5247084 3.244467 2.0213867
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.6649579 3.2026732 3.5902215 11.765494 7.295397
#> Trackway_02 1.9906179 1.4098052 0.7174954 -1.000000 -1.000000
#> Trackway_03 0.9838750 1.1436289 0.9502979 8.597355 5.517615
#> Trackway_04 3.7109784 3.3643773 2.5437094 10.921039 8.414166
#> Trackway_07 0.8804758 0.8238755 1.5483503 9.187851 5.242062
#> Trackway_08 NA 0.7155646 1.3409034 8.518367 4.933532
#> Trackway_09 0.7155646 NA 0.9244429 -1.000000 5.573580
#> Trackway_13 1.3409034 0.9244429 NA -1.000000 6.253160
#> Trackway_15 8.5183671 -1.0000000 -1.0000000 NA 5.047933
#> Trackway_16 4.9335320 5.5735796 6.2531599 5.047933 NA
#> Trackway_18 1.1308585 1.5527833 1.9590867 8.086916 -1.000000
#> Trackway_18
#> Trackway_01 4.6697839
#> Trackway_02 2.1724744
#> Trackway_03 0.5247084
#> Trackway_04 3.2444674
#> Trackway_07 2.0213867
#> Trackway_08 1.1308585
#> Trackway_09 1.5527833
#> Trackway_13 1.9590867
#> Trackway_15 8.0869164
#> Trackway_16 -1.0000000
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[96]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0.9168472 3.2654573 1.653481 2.3071368
#> Trackway_02 0.9168472 NA 2.6153991 2.064047 1.4230331
#> Trackway_03 3.2654573 2.6153991 NA 5.036200 1.7653723
#> Trackway_04 1.6534812 2.0640471 5.0362002 NA 3.3596431
#> Trackway_07 2.3071368 1.4230331 1.7653723 3.359643 NA
#> Trackway_08 3.1079645 2.1078872 2.0522090 3.998155 0.6864851
#> Trackway_09 2.3828561 1.8560316 0.8207815 3.866874 1.3255364
#> Trackway_13 2.8453930 2.6268788 1.1097553 4.426780 2.3112424
#> Trackway_15 11.4406086 -1.0000000 -1.0000000 -1.000000 9.2975475
#> Trackway_16 7.6471470 6.7412466 5.4274549 8.392554 -1.0000000
#> Trackway_18 3.1234091 2.4374246 0.5080468 4.499935 1.3699581
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.1079645 2.3828561 2.845393 11.440609 7.647147
#> Trackway_02 2.1078872 1.8560316 2.626879 -1.000000 6.741247
#> Trackway_03 2.0522090 0.8207815 1.109755 -1.000000 5.427455
#> Trackway_04 3.9981546 3.8668738 4.426780 -1.000000 8.392554
#> Trackway_07 0.6864851 1.3255364 2.311242 9.297548 -1.000000
#> Trackway_08 NA 1.6070965 2.696932 8.661829 4.668147
#> Trackway_09 1.6070965 NA 1.062323 -1.000000 -1.000000
#> Trackway_13 2.6969316 1.0623227 NA -1.000000 6.536198
#> Trackway_15 8.6618288 -1.0000000 -1.000000 NA -1.000000
#> Trackway_16 4.6681474 -1.0000000 6.536198 -1.000000 NA
#> Trackway_18 1.2256307 0.8776005 1.903461 -1.000000 -1.000000
#> Trackway_18
#> Trackway_01 3.1234091
#> Trackway_02 2.4374246
#> Trackway_03 0.5080468
#> Trackway_04 4.4999349
#> Trackway_07 1.3699581
#> Trackway_08 1.2256307
#> Trackway_09 0.8776005
#> Trackway_13 1.9034614
#> Trackway_15 -1.0000000
#> Trackway_16 -1.0000000
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[97]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0.9388301 4.2337255 1.224495 2.0075205
#> Trackway_02 0.9388301 NA 2.6149273 1.471734 1.5109299
#> Trackway_03 4.2337255 2.6149273 NA 4.249286 2.1016145
#> Trackway_04 1.2244953 1.4717340 4.2492857 NA 2.9266546
#> Trackway_07 2.0075205 1.5109299 2.1016145 2.926655 NA
#> Trackway_08 2.7579841 2.1900679 1.8478847 3.642376 0.7842861
#> Trackway_09 2.8075886 1.8711333 0.9134863 3.116423 1.8963606
#> Trackway_13 1.8656075 0.8519252 1.7633404 2.237307 1.2346814
#> Trackway_15 11.5173110 10.7725908 8.3682024 12.220594 -1.0000000
#> Trackway_16 7.2555114 6.8093420 -1.0000000 8.239402 -1.0000000
#> Trackway_18 3.4181285 2.5361141 0.2227078 3.910556 1.9156825
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 2.7579841 2.8075886 1.8656075 11.517311 7.255511
#> Trackway_02 2.1900679 1.8711333 0.8519252 10.772591 6.809342
#> Trackway_03 1.8478847 0.9134863 1.7633404 8.368202 -1.000000
#> Trackway_04 3.6423763 3.1164234 2.2373073 12.220594 8.239402
#> Trackway_07 0.7842861 1.8963606 1.2346814 -1.000000 -1.000000
#> Trackway_08 NA 2.0831443 1.6925821 8.798781 -1.000000
#> Trackway_09 2.0831443 NA 1.0553095 -1.000000 6.094863
#> Trackway_13 1.6925821 1.0553095 NA 9.985224 6.266654
#> Trackway_15 8.7987813 -1.0000000 9.9852240 NA 5.531908
#> Trackway_16 -1.0000000 6.0948634 6.2666536 5.531908 NA
#> Trackway_18 1.5969933 1.0221861 1.6911125 8.357864 5.195211
#> Trackway_18
#> Trackway_01 3.4181285
#> Trackway_02 2.5361141
#> Trackway_03 0.2227078
#> Trackway_04 3.9105555
#> Trackway_07 1.9156825
#> Trackway_08 1.5969933
#> Trackway_09 1.0221861
#> Trackway_13 1.6911125
#> Trackway_15 8.3578635
#> Trackway_16 5.1952110
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[98]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0.8565315 3.4184989 0.7947659 2.3400037
#> Trackway_02 0.8565315 NA 2.5771590 1.6337440 1.5664652
#> Trackway_03 3.4184989 2.5771590 NA 4.2870653 1.5205223
#> Trackway_04 0.7947659 1.6337440 4.2870653 NA 3.0766137
#> Trackway_07 2.3400037 1.5664652 1.5205223 3.0766137 NA
#> Trackway_08 3.0667850 2.2611496 0.9676088 3.8189788 0.7547623
#> Trackway_09 2.8557328 2.0172236 0.5808502 3.6499238 1.2059078
#> Trackway_13 3.1690881 2.3045954 1.2148227 3.8278588 1.9584635
#> Trackway_15 -1.0000000 11.5079057 9.0944703 -1.0000000 -1.0000000
#> Trackway_16 7.1511708 6.4933961 4.8816308 7.7582998 4.9564189
#> Trackway_18 2.8887594 2.1031057 1.1845559 3.6269176 0.5504416
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.0667850 2.8557328 3.1690881 -1.000000 7.151171
#> Trackway_02 2.2611496 2.0172236 2.3045954 11.507906 6.493396
#> Trackway_03 0.9676088 0.5808502 1.2148227 9.094470 4.881631
#> Trackway_04 3.8189788 3.6499238 3.8278588 -1.000000 7.758300
#> Trackway_07 0.7547623 1.2059078 1.9584635 -1.000000 4.956419
#> Trackway_08 NA 0.9815176 1.8681092 9.252586 -1.000000
#> Trackway_09 0.9815176 NA 0.8902185 -1.000000 5.280827
#> Trackway_13 1.8681092 0.8902185 NA 10.014729 -1.000000
#> Trackway_15 9.2525855 -1.0000000 10.0147286 NA -1.000000
#> Trackway_16 -1.0000000 5.2808269 -1.0000000 -1.000000 NA
#> Trackway_18 0.2510200 1.1972984 1.9871769 -1.000000 4.485767
#> Trackway_18
#> Trackway_01 2.8887594
#> Trackway_02 2.1031057
#> Trackway_03 1.1845559
#> Trackway_04 3.6269176
#> Trackway_07 0.5504416
#> Trackway_08 0.2510200
#> Trackway_09 1.1972984
#> Trackway_13 1.9871769
#> Trackway_15 -1.0000000
#> Trackway_16 4.4857673
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[99]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 2.531251 4.5903987 1.325067 3.0579214
#> Trackway_02 2.531251 NA 2.6927635 1.866076 2.3022427
#> Trackway_03 4.590399 2.692763 NA 4.635893 2.1883958
#> Trackway_04 1.325067 1.866076 4.6358931 NA 3.1541618
#> Trackway_07 3.057921 2.302243 2.1883958 3.154162 NA
#> Trackway_08 3.436343 2.381198 1.5663515 3.636111 0.7135184
#> Trackway_09 3.382863 1.640047 1.2088304 3.231725 1.2375581
#> Trackway_13 3.372471 1.277622 1.4703277 2.970145 1.6178999
#> Trackway_15 12.259188 11.024079 8.4286333 12.547888 -1.0000000
#> Trackway_16 7.075234 6.838503 -1.0000000 -1.000000 -1.0000000
#> Trackway_18 4.771344 2.832758 0.2021652 4.573176 2.2636149
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 3.4363429 3.3828634 3.372471 12.259188 7.075234
#> Trackway_02 2.3811983 1.6400467 1.277622 11.024079 6.838503
#> Trackway_03 1.5663515 1.2088304 1.470328 8.428633 -1.000000
#> Trackway_04 3.6361106 3.2317248 2.970145 12.547888 -1.000000
#> Trackway_07 0.7135184 1.2375581 1.617900 -1.000000 -1.000000
#> Trackway_08 NA 0.9585954 1.610369 -1.000000 -1.000000
#> Trackway_09 0.9585954 NA 0.659504 9.399167 -1.000000
#> Trackway_13 1.6103693 0.6595040 NA -1.000000 -1.000000
#> Trackway_15 -1.0000000 9.3991668 -1.000000 NA 6.010635
#> Trackway_16 -1.0000000 -1.0000000 -1.000000 6.010635 NA
#> Trackway_18 1.7520977 1.3909393 1.644844 8.273156 -1.000000
#> Trackway_18
#> Trackway_01 4.7713436
#> Trackway_02 2.8327579
#> Trackway_03 0.2021652
#> Trackway_04 4.5731759
#> Trackway_07 2.2636149
#> Trackway_08 1.7520977
#> Trackway_09 1.3909393
#> Trackway_13 1.6448437
#> Trackway_15 8.2731565
#> Trackway_16 -1.0000000
#> Trackway_18 NA
#>
#> $Frechet_distance_metric_simulations[[100]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 3.2186075 5.2089916 2.113133 3.1636650
#> Trackway_02 3.218607 NA 2.6356308 1.798007 1.7208177
#> Trackway_03 5.208992 2.6356308 NA 4.336081 1.9549269
#> Trackway_04 2.113133 1.7980074 4.3360809 NA 2.8924840
#> Trackway_07 3.163665 1.7208177 1.9549269 2.892484 NA
#> Trackway_08 4.310507 2.3680025 1.2250893 3.804173 0.9759495
#> Trackway_09 4.182962 2.0306537 0.9175078 3.612995 1.0378827
#> Trackway_13 3.855531 0.9803119 2.1145545 2.715964 1.2224436
#> Trackway_15 -1.000000 10.6169599 -1.0000000 11.972559 -1.0000000
#> Trackway_16 6.903167 7.1348434 5.7538098 -1.000000 5.4140285
#> Trackway_18 4.153981 2.4932546 1.1016428 3.789600 0.9995772
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 4.3105068 4.1829624 3.8555313 -1.000000 6.903167
#> Trackway_02 2.3680025 2.0306537 0.9803119 10.616960 7.134843
#> Trackway_03 1.2250893 0.9175078 2.1145545 -1.000000 5.753810
#> Trackway_04 3.8041730 3.6129948 2.7159641 11.972559 -1.000000
#> Trackway_07 0.9759495 1.0378827 1.2224436 -1.000000 5.414029
#> Trackway_08 NA 0.5063670 1.5643756 8.258095 4.995433
#> Trackway_09 0.5063670 NA 1.0996397 8.597608 -1.000000
#> Trackway_13 1.5643756 1.0996397 NA -1.000000 -1.000000
#> Trackway_15 8.2580950 8.5976078 -1.0000000 NA -1.000000
#> Trackway_16 4.9954329 -1.0000000 -1.0000000 -1.000000 NA
#> Trackway_18 0.1404792 0.3811636 1.4682676 8.317186 -1.000000
#> Trackway_18
#> Trackway_01 4.1539808
#> Trackway_02 2.4932546
#> Trackway_03 1.1016428
#> Trackway_04 3.7896005
#> Trackway_07 0.9995772
#> Trackway_08 0.1404792
#> Trackway_09 0.3811636
#> Trackway_13 1.4682676
#> Trackway_15 8.3171860
#> Trackway_16 -1.0000000
#> Trackway_18 NAThe resulting track similarity objects
can then be explored to check pairwise distances,
p-values, and combined
p-values. It is important to verify the presence of
invalid measurements (-1) in the results, especially
when working with highly disparate tracks generated by
Unconstrained models.
Intersection Metric Calculation for Tracks
The track_intersection() function is
designed to detect and quantify unique intersections
between real movement trajectories, helping to identify
behavioral interactions such as coordinated movement,
chasing, or random exploration. By
comparing actual tracks against simulated trajectories generated with
the simulate_track() function, users can
statistically assess whether observed intersections occur more or less
frequently than expected under random conditions.
The input to this function is a track R
object. If statistical testing is desired,
test argument must be set
TRUE and a
track simulation R object provided via the
sim argument.
The function offers several options for modifying the
starting positions of simulated tracks, controlled by
the origin.permutation argument. When set
to "None", simulated trajectories retain
their original starting points, making them comparable to the actual
data without spatial modification. The
"Min.Box" option randomly places the
starting points of simulated tracks within the minimum bounding
box surrounding all original starting points, simulating
movement within a defined area. The
"Conv.Hull" option provides a more precise
alternative by placing simulated tracks within the convex
hull encompassing all original starting points, reflecting the
actual space occupied by the tracks. The
"Custom" option allows users to specify an
area of interest by providing a set of coordinates
(custom.coord) defining the region’s
vertices, which is particularly useful when prior knowledge of terrain
features or environmental factors suggests that movement may be
spatially constrained.
The H1 argument specifies the
alternative hypothesis to be tested. When set to
"Lower", the function evaluates whether
the observed intersections are significantly fewer than those generated
by simulations, which may indicate coordinated or gregarious
movement. When set to "Higher",
it tests whether the observed intersections are significantly greater,
which could be indicative of predatory or chasing
interactions. Users must provide a value for
H1 when the
test argument is set to
TRUE.
The output of the track_intersection()
function is a track intersection R object
that provides a comprehensive assessment of how tracks intersect and,
when applicable, how these intersections compare to simulated datasets.
The core component of this object is the
Intersection_metric, a matrix that details
the number of unique intersection points between pairs of trajectories.
When test = TRUE, which requires a
track simulation R object generated via
simulate_track() provided through the
sim argument, the function produces
additional outputs aimed at statistically evaluating the observed
intersections. One of these is the
Intersection_metric_p_values matrix, which
compares the observed intersections to those derived from simulations.
Each p-value in this matrix indicates the proportion of
simulated datasets with intersection counts as extreme or more extreme
than the observed ones, depending on the selected
H1 hypothesis (whether intersections are
expected to be fewer or more frequent than random expectation). The
function also returns the
Intersection_metric_p_values_combined, a
single value that summarizes the overall statistical significance of the
intersection metrics across all trajectory pairs. This combined
p-value provides a general indication of whether the total
number of intersections observed is significantly different from those
generated through simulations, either supporting or rejecting the
hypothesis under investigation. Additionally, the function provides the
Intersection_metric_simulations, a list
containing matrices of intersection counts for each simulation
iteration. This detailed output allows users to explore how the number
of intersections varies across multiple randomized scenarios, providing
deeper insights into the robustness and consistency of the observed
patterns. By comparing these results to simulated tracks, researchers
can better evaluate whether the observed intersections are genuinely
meaningful or simply the result of random chance.
Examples of Usage
Detecting intersections between Paluxy River tracks and simulated tracks generated using the Directed model, without modifying the starting positions, and testing for reduced intersections.
int_directed_paluxy <- track_intersection(PaluxyRiver, test = TRUE, H1 = "Lower",
sim = sim_directed_paluxy,
origin.permutation = "None")
print(int_directed_paluxy)#> $Intersection_metric
#> Trackway_1 Trackway_2
#> Trackway_1 NA 1
#> Trackway_2 1 NA
#>
#> $Intersection_metric_p_values
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.5742574
#> Trackway_2 0.5742574 NA
#>
#> $Intersection_metric_p_values_BH
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.5742574
#> Trackway_2 0.5742574 NA
#>
#> $Intersection_metric_p_values_combined
#> [1] 0.5742574
#>
#> $Intersection_metric_simulations
#> $Intersection_metric_simulations[[1]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 1
#> Trackway_2 1 NA
#>
#> $Intersection_metric_simulations[[2]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 1
#> Trackway_2 1 NA
#>
#> $Intersection_metric_simulations[[3]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 5
#> Trackway_2 5 NA
#>
#> $Intersection_metric_simulations[[4]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 1
#> Trackway_2 1 NA
#>
#> $Intersection_metric_simulations[[5]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0
#> Trackway_2 0 NA
#>
#> $Intersection_metric_simulations[[6]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0
#> Trackway_2 0 NA
#>
#> $Intersection_metric_simulations[[7]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 3
#> Trackway_2 3 NA
#>
#> $Intersection_metric_simulations[[8]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 1
#> Trackway_2 1 NA
#>
#> $Intersection_metric_simulations[[9]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0
#> Trackway_2 0 NA
#>
#> $Intersection_metric_simulations[[10]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 4
#> Trackway_2 4 NA
#>
#> $Intersection_metric_simulations[[11]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 3
#> Trackway_2 3 NA
#>
#> $Intersection_metric_simulations[[12]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 2
#> Trackway_2 2 NA
#>
#> $Intersection_metric_simulations[[13]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 1
#> Trackway_2 1 NA
#>
#> $Intersection_metric_simulations[[14]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0
#> Trackway_2 0 NA
#>
#> $Intersection_metric_simulations[[15]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 1
#> Trackway_2 1 NA
#>
#> $Intersection_metric_simulations[[16]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 1
#> Trackway_2 1 NA
#>
#> $Intersection_metric_simulations[[17]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 1
#> Trackway_2 1 NA
#>
#> $Intersection_metric_simulations[[18]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 3
#> Trackway_2 3 NA
#>
#> $Intersection_metric_simulations[[19]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0
#> Trackway_2 0 NA
#>
#> $Intersection_metric_simulations[[20]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 3
#> Trackway_2 3 NA
#>
#> $Intersection_metric_simulations[[21]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 2
#> Trackway_2 2 NA
#>
#> $Intersection_metric_simulations[[22]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 3
#> Trackway_2 3 NA
#>
#> $Intersection_metric_simulations[[23]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 1
#> Trackway_2 1 NA
#>
#> $Intersection_metric_simulations[[24]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0
#> Trackway_2 0 NA
#>
#> $Intersection_metric_simulations[[25]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 3
#> Trackway_2 3 NA
#>
#> $Intersection_metric_simulations[[26]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0
#> Trackway_2 0 NA
#>
#> $Intersection_metric_simulations[[27]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 9
#> Trackway_2 9 NA
#>
#> $Intersection_metric_simulations[[28]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 1
#> Trackway_2 1 NA
#>
#> $Intersection_metric_simulations[[29]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 3
#> Trackway_2 3 NA
#>
#> $Intersection_metric_simulations[[30]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0
#> Trackway_2 0 NA
#>
#> $Intersection_metric_simulations[[31]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0
#> Trackway_2 0 NA
#>
#> $Intersection_metric_simulations[[32]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0
#> Trackway_2 0 NA
#>
#> $Intersection_metric_simulations[[33]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 1
#> Trackway_2 1 NA
#>
#> $Intersection_metric_simulations[[34]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 6
#> Trackway_2 6 NA
#>
#> $Intersection_metric_simulations[[35]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 4
#> Trackway_2 4 NA
#>
#> $Intersection_metric_simulations[[36]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 3
#> Trackway_2 3 NA
#>
#> $Intersection_metric_simulations[[37]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 1
#> Trackway_2 1 NA
#>
#> $Intersection_metric_simulations[[38]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 1
#> Trackway_2 1 NA
#>
#> $Intersection_metric_simulations[[39]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 3
#> Trackway_2 3 NA
#>
#> $Intersection_metric_simulations[[40]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 1
#> Trackway_2 1 NA
#>
#> $Intersection_metric_simulations[[41]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 5
#> Trackway_2 5 NA
#>
#> $Intersection_metric_simulations[[42]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 3
#> Trackway_2 3 NA
#>
#> $Intersection_metric_simulations[[43]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 2
#> Trackway_2 2 NA
#>
#> $Intersection_metric_simulations[[44]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0
#> Trackway_2 0 NA
#>
#> $Intersection_metric_simulations[[45]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0
#> Trackway_2 0 NA
#>
#> $Intersection_metric_simulations[[46]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 1
#> Trackway_2 1 NA
#>
#> $Intersection_metric_simulations[[47]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 1
#> Trackway_2 1 NA
#>
#> $Intersection_metric_simulations[[48]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 2
#> Trackway_2 2 NA
#>
#> $Intersection_metric_simulations[[49]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 1
#> Trackway_2 1 NA
#>
#> $Intersection_metric_simulations[[50]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 3
#> Trackway_2 3 NA
#>
#> $Intersection_metric_simulations[[51]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 3
#> Trackway_2 3 NA
#>
#> $Intersection_metric_simulations[[52]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 3
#> Trackway_2 3 NA
#>
#> $Intersection_metric_simulations[[53]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0
#> Trackway_2 0 NA
#>
#> $Intersection_metric_simulations[[54]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 4
#> Trackway_2 4 NA
#>
#> $Intersection_metric_simulations[[55]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 1
#> Trackway_2 1 NA
#>
#> $Intersection_metric_simulations[[56]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 2
#> Trackway_2 2 NA
#>
#> $Intersection_metric_simulations[[57]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 5
#> Trackway_2 5 NA
#>
#> $Intersection_metric_simulations[[58]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 1
#> Trackway_2 1 NA
#>
#> $Intersection_metric_simulations[[59]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 5
#> Trackway_2 5 NA
#>
#> $Intersection_metric_simulations[[60]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 1
#> Trackway_2 1 NA
#>
#> $Intersection_metric_simulations[[61]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0
#> Trackway_2 0 NA
#>
#> $Intersection_metric_simulations[[62]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 1
#> Trackway_2 1 NA
#>
#> $Intersection_metric_simulations[[63]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 1
#> Trackway_2 1 NA
#>
#> $Intersection_metric_simulations[[64]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 5
#> Trackway_2 5 NA
#>
#> $Intersection_metric_simulations[[65]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0
#> Trackway_2 0 NA
#>
#> $Intersection_metric_simulations[[66]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 1
#> Trackway_2 1 NA
#>
#> $Intersection_metric_simulations[[67]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 1
#> Trackway_2 1 NA
#>
#> $Intersection_metric_simulations[[68]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 2
#> Trackway_2 2 NA
#>
#> $Intersection_metric_simulations[[69]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 1
#> Trackway_2 1 NA
#>
#> $Intersection_metric_simulations[[70]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0
#> Trackway_2 0 NA
#>
#> $Intersection_metric_simulations[[71]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 1
#> Trackway_2 1 NA
#>
#> $Intersection_metric_simulations[[72]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 1
#> Trackway_2 1 NA
#>
#> $Intersection_metric_simulations[[73]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 1
#> Trackway_2 1 NA
#>
#> $Intersection_metric_simulations[[74]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 2
#> Trackway_2 2 NA
#>
#> $Intersection_metric_simulations[[75]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 5
#> Trackway_2 5 NA
#>
#> $Intersection_metric_simulations[[76]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 4
#> Trackway_2 4 NA
#>
#> $Intersection_metric_simulations[[77]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 1
#> Trackway_2 1 NA
#>
#> $Intersection_metric_simulations[[78]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 3
#> Trackway_2 3 NA
#>
#> $Intersection_metric_simulations[[79]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 1
#> Trackway_2 1 NA
#>
#> $Intersection_metric_simulations[[80]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 1
#> Trackway_2 1 NA
#>
#> $Intersection_metric_simulations[[81]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0
#> Trackway_2 0 NA
#>
#> $Intersection_metric_simulations[[82]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 5
#> Trackway_2 5 NA
#>
#> $Intersection_metric_simulations[[83]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0
#> Trackway_2 0 NA
#>
#> $Intersection_metric_simulations[[84]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 3
#> Trackway_2 3 NA
#>
#> $Intersection_metric_simulations[[85]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 2
#> Trackway_2 2 NA
#>
#> $Intersection_metric_simulations[[86]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 1
#> Trackway_2 1 NA
#>
#> $Intersection_metric_simulations[[87]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 2
#> Trackway_2 2 NA
#>
#> $Intersection_metric_simulations[[88]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 3
#> Trackway_2 3 NA
#>
#> $Intersection_metric_simulations[[89]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0
#> Trackway_2 0 NA
#>
#> $Intersection_metric_simulations[[90]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 1
#> Trackway_2 1 NA
#>
#> $Intersection_metric_simulations[[91]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 1
#> Trackway_2 1 NA
#>
#> $Intersection_metric_simulations[[92]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0
#> Trackway_2 0 NA
#>
#> $Intersection_metric_simulations[[93]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0
#> Trackway_2 0 NA
#>
#> $Intersection_metric_simulations[[94]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0
#> Trackway_2 0 NA
#>
#> $Intersection_metric_simulations[[95]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 8
#> Trackway_2 8 NA
#>
#> $Intersection_metric_simulations[[96]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0
#> Trackway_2 0 NA
#>
#> $Intersection_metric_simulations[[97]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 2
#> Trackway_2 2 NA
#>
#> $Intersection_metric_simulations[[98]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 2
#> Trackway_2 2 NA
#>
#> $Intersection_metric_simulations[[99]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 3
#> Trackway_2 3 NA
#>
#> $Intersection_metric_simulations[[100]]
#> Trackway_1 Trackway_2
#> Trackway_1 NA 3
#> Trackway_2 3 NADetecting intersections between MountTom tracks (after subsetting) and simulated tracks generated using the Constrained model, with convex hull permutation of starting points, and testing for increased intersections.
int_constrained_mount <- track_intersection(sbMountTom, test = TRUE, H1 = "Higher",
sim = sim_constrained_mount,
origin.permutation = "Conv.Hull")
print(int_constrained_mount)#> $Intersection_metric
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 1
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 1 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_p_values
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1 1 1 1.0000000
#> Trackway_02 1 NA 1 1 1.0000000
#> Trackway_03 1 1 NA 1 1.0000000
#> Trackway_04 1 1 1 NA 1.0000000
#> Trackway_07 1 1 1 1 NA
#> Trackway_08 1 1 1 1 1.0000000
#> Trackway_09 1 1 1 1 0.1089109
#> Trackway_13 1 1 1 1 1.0000000
#> Trackway_15 1 1 1 1 1.0000000
#> Trackway_16 1 1 1 1 1.0000000
#> Trackway_18 1 1 1 1 1.0000000
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 1 1.0000000 1 1 1
#> Trackway_02 1 1.0000000 1 1 1
#> Trackway_03 1 1.0000000 1 1 1
#> Trackway_04 1 1.0000000 1 1 1
#> Trackway_07 1 0.1089109 1 1 1
#> Trackway_08 NA 1.0000000 1 1 1
#> Trackway_09 1 NA 1 1 1
#> Trackway_13 1 1.0000000 NA 1 1
#> Trackway_15 1 1.0000000 1 NA 1
#> Trackway_16 1 1.0000000 1 1 NA
#> Trackway_18 1 1.0000000 1 1 1
#> Trackway_18
#> Trackway_01 1
#> Trackway_02 1
#> Trackway_03 1
#> Trackway_04 1
#> Trackway_07 1
#> Trackway_08 1
#> Trackway_09 1
#> Trackway_13 1
#> Trackway_15 1
#> Trackway_16 1
#> Trackway_18 NA
#>
#> $Intersection_metric_p_values_BH
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1 1 1 1
#> Trackway_02 1 NA 1 1 1
#> Trackway_03 1 1 NA 1 1
#> Trackway_04 1 1 1 NA 1
#> Trackway_07 1 1 1 1 NA
#> Trackway_08 1 1 1 1 1
#> Trackway_09 1 1 1 1 1
#> Trackway_13 1 1 1 1 1
#> Trackway_15 1 1 1 1 1
#> Trackway_16 1 1 1 1 1
#> Trackway_18 1 1 1 1 1
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 1 1 1 1 1
#> Trackway_02 1 1 1 1 1
#> Trackway_03 1 1 1 1 1
#> Trackway_04 1 1 1 1 1
#> Trackway_07 1 1 1 1 1
#> Trackway_08 NA 1 1 1 1
#> Trackway_09 1 NA 1 1 1
#> Trackway_13 1 1 NA 1 1
#> Trackway_15 1 1 1 NA 1
#> Trackway_16 1 1 1 1 NA
#> Trackway_18 1 1 1 1 1
#> Trackway_18
#> Trackway_01 1
#> Trackway_02 1
#> Trackway_03 1
#> Trackway_04 1
#> Trackway_07 1
#> Trackway_08 1
#> Trackway_09 1
#> Trackway_13 1
#> Trackway_15 1
#> Trackway_16 1
#> Trackway_18 NA
#>
#> $Intersection_metric_p_values_combined
#> [1] 0.7425743
#>
#> $Intersection_metric_simulations
#> $Intersection_metric_simulations[[1]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 1 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 1 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[2]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 1 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 1 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 1 0 1 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 1 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 1 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 1
#> Trackway_16 0 0 0 1 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[3]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 1
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 1 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[4]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 1
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 1 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 1 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 1 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[5]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 1
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 1 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[6]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 1 0 0
#> Trackway_09 0 0 1 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 1 1 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 1 0 0 0
#> Trackway_09 1 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[7]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 1
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 1 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[8]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 1 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 1 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[9]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 1 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 1
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 1 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 1 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[10]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[11]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 1
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 1 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[12]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[13]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[14]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[15]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[16]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[17]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 1 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 1 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 1 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 1
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 1 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 1
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[18]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 1 0
#> Trackway_15 0 0 1 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[19]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[20]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[21]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 1
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 1 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[22]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 1 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 1 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 1 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 1 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[23]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 1 0
#> Trackway_15 0 0 1 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[24]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 1
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 1 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[25]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 1
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 1 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 1
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 1 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[26]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 1 0 0 0
#> Trackway_09 1 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[27]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[28]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1 0 0 0
#> Trackway_02 1 NA 0 0 0
#> Trackway_03 0 0 NA 1 0
#> Trackway_04 0 0 1 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[29]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 1 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 1 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[30]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 1
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 1 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[31]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1 0 0 0
#> Trackway_02 1 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 1
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 1 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[32]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 1 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 1 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[33]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 1 1
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 1 0 0 0
#> Trackway_07 0 1 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[34]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 1
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 1 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[35]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[36]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 1
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 1 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[37]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 1 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 1 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 1
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 1 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[38]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 1 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 1 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 1 0 0 0
#> Trackway_09 1 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[39]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 1 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 1
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[40]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 1
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 1 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 1 0
#> Trackway_15 0 0 1 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 1 0 0 1
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 1
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 1
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[41]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 1 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 1 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[42]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 1
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 1 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[43]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[44]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 1 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 1 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 1 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 1 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 1 0 0 0
#> Trackway_09 1 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[45]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 1 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 1 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[46]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1 0 0 0
#> Trackway_02 1 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 1
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 1 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[47]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 1 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 1
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[48]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 1 0 1 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 1 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 1 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 1 0 0 0
#> Trackway_09 1 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[49]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 1
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 1 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[50]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 1 0 1
#> Trackway_03 0 1 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 1 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[51]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 1 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 1 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[52]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 1 0 0 0
#> Trackway_09 1 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[53]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[54]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 1 0 0
#> Trackway_02 0 NA 1 0 0
#> Trackway_03 1 1 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 1 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 1 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 1
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 1
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[55]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 1 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 1 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[56]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[57]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 1 0 0
#> Trackway_03 0 1 NA 1 0
#> Trackway_04 0 0 1 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 1
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 1 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[58]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[59]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 1 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 1 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 1
#> Trackway_16 0 0 0 1 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[60]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 1
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 1 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[61]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 1 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 1
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[62]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 1 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 1 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 1 1
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 1 0 0 0
#> Trackway_07 0 1 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[63]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 1 0
#> Trackway_04 0 0 1 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 1 1 0
#> Trackway_13 0 1 NA 1 0
#> Trackway_15 0 1 1 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[64]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[65]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[66]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1 0 0 0
#> Trackway_02 1 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 1
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 1 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[67]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 1
#> Trackway_07 0 0 0 1 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[68]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[69]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 1 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 1 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[70]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 1 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 1 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[71]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 1
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 1 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[72]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 1
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 1 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[73]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 1
#> Trackway_07 0 0 0 1 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[74]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1 0 0 0
#> Trackway_02 1 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 1
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 1 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[75]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[76]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[77]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 1
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 1 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[78]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1 0 0 0
#> Trackway_02 1 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 1 1 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 1 0 0 0
#> Trackway_02 0 1 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 1
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 1 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[79]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[80]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 1 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 1 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 1 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 1
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[81]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[82]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 1 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 1 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[83]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[84]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 1 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 1 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[85]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 1
#> Trackway_07 0 0 0 1 NA
#> Trackway_08 0 3 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 3 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[86]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 1
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 1 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 1 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 1 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[87]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 1 0 0 0
#> Trackway_02 1 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 1
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 1 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[88]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 1 0
#> Trackway_09 0 0 0 1 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 1 1 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 1 0 0 0
#> Trackway_09 1 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[89]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 1 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 1 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[90]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 1
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 1 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[91]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[92]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 1 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 1 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[93]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 1
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 1 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[94]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 1
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 1 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 1 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 1 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[95]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 1 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 1
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[96]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[97]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 1
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 1 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[98]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[99]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 0
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 0
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NA
#>
#> $Intersection_metric_simulations[[100]]
#> Trackway_01 Trackway_02 Trackway_03 Trackway_04 Trackway_07
#> Trackway_01 NA 0 0 0 0
#> Trackway_02 0 NA 0 0 0
#> Trackway_03 0 0 NA 0 0
#> Trackway_04 0 0 0 NA 0
#> Trackway_07 0 0 0 0 NA
#> Trackway_08 0 0 0 0 0
#> Trackway_09 0 0 0 0 0
#> Trackway_13 0 0 0 0 0
#> Trackway_15 0 0 0 0 0
#> Trackway_16 0 0 0 0 1
#> Trackway_18 0 0 0 0 0
#> Trackway_08 Trackway_09 Trackway_13 Trackway_15 Trackway_16
#> Trackway_01 0 0 0 0 0
#> Trackway_02 0 0 0 0 0
#> Trackway_03 0 0 0 0 0
#> Trackway_04 0 0 0 0 0
#> Trackway_07 0 0 0 0 1
#> Trackway_08 NA 0 0 0 0
#> Trackway_09 0 NA 0 0 0
#> Trackway_13 0 0 NA 0 0
#> Trackway_15 0 0 0 NA 0
#> Trackway_16 0 0 0 0 NA
#> Trackway_18 0 0 0 0 0
#> Trackway_18
#> Trackway_01 0
#> Trackway_02 0
#> Trackway_03 0
#> Trackway_04 0
#> Trackway_07 0
#> Trackway_08 0
#> Trackway_09 0
#> Trackway_13 0
#> Trackway_15 0
#> Trackway_16 0
#> Trackway_18 NACombining P-values from Multiple Similarity and Intersection Metrics
The combined_prob() function is
designed to combine p-values obtained from
various similarity and intersection metrics to provide
a more comprehensive assessment of how well the observed
trajectories compare to those generated through simulation. The
function is useful when multiple metrics are applied to the same set of
data, as it allows users to integrate the results and obtain an
overall measure of significance.
The basic idea behind this function is to assess how the
observed similarity or intersection metrics compare to
those generated under various simulated scenarios. It
starts by receiving a list of track similarity
and/or track intersection R objects, obtained from
simil_DTW_metric(),
simil_Frechet_metric(), and/or
track_intersection() functions. To make
meaningful comparisons, the function ensures that all metrics provided
in the metrics list have been derived
using the same number of simulations. If the metrics are incompatible,
the function raises an error to prevent incorrect calculations. The
process works by generating a matrix of
p-values where each entry represents the
combined significance of multiple metrics for a particular
trajectory pair. The function also provides an overall
p-value that summarizes the combined significance
across all trajectory pairs. This value indicates how
consistently the observed data differs from the simulated
datasets across all metrics.
The result is returned as a list consisting of two main components. The first component is a matrix of combined p-values for each trajectory pair, where the entries indicate the probability of observing the combined metrics across all simulations. This matrix provides a detailed comparison of how individual track pairs compare to the simulated datasets. The second component is a single overall p-value that summarizes the combined significance of all metrics across all pairs of trajectories, offering a comprehensive assessment of the dataset as a whole.
The combined_prob() function provides
an efficient way to aggregate multiple similarity or
intersection metrics, making it an essential tool for users who
wish to comprehensively evaluate their models and
hypotheses. By allowing for the integration of different
metrics, the function offers a holistic approach to analyzing
and comparing track data.
Examples of Usage
Combining p-values for the Paluxy River
dataset based on analyses performed with the Directed model
simulations. In this example, we combine results from three
different methods: Dynamic Time Warping (DTW),
Fréchet distance, and intersection
counts. All of them were computed using the same simulated
dataset (sim_directed_paluxy) and are stored in the objects
simil_dtw_directed_paluxy,
simil_frechet_directed_paluxy, and
int_directed_paluxy.
combined_metrics_paluxy <- combined_prob(PaluxyRiver, metrics = list(
simil_dtw_directed_paluxy,
simil_frechet_directed_paluxy,
int_directed_paluxy
))#> $P_values
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.05940594
#> Trackway_2 0.05940594 NA
#>
#> $P_values_BH
#> Trackway_1 Trackway_2
#> Trackway_1 NA 0.05940594
#> Trackway_2 0.05940594 NA
#>
#> $P_values_global
#> [1] 0.05940594Clustering Tracks Based on Movement Parameters
Clustering tracks is a powerful approach for
detecting patterns of movement that may reveal specific
behaviors or strategies employed by trackmakers. The
cluster_track() function is designed to
process a set of tracks by calculating various movement
parameters and then classifying them into groups based on their
similarities. Instead of just comparing tracks
pairwise, this method allows for the identification of broader
behavioral patterns shared across multiple tracks.
The process begins with preparing the data, where tracks containing fewer than four steps are filtered out. Short tracks lack sufficient information about movement patterns and would introduce noise into the clustering process. Once filtered, the function calculates multiple movement parameters to characterize the trackmaker’s behavior. These parameters include metrics such as turning angles, step lengths, sinuosity, straightness, and velocity.
The cluster_track() function uses the
mclust package to perform
model-based clustering, which is particularly effective
because it identifies natural clusters by fitting
various Gaussian mixture models to the data. Unlike
methods that impose arbitrary groupings, model-based
clustering selects the most suitable model by optimizing the
Bayesian Information Criterion (BIC). This approach is
versatile, supporting single-parameter and multi-parameter
clustering, depending on the user’s analytical needs. When
only one parameter is selected, the function uses
simpler models with equal or variable variance. When
multiple parameters are specified, it examines the
entire range of Gaussian models provided by
mclust.
The parameters used for clustering are specified via the
variables argument. Users can choose from
a variety of options, including "TurnAng"
(mean turning angle), "sdTurnAng"
(standard deviation of turning angles),
"Distance" (total distance covered),
"Length" (total length of the trajectory),
"StLength" (mean step length),
"sdStLength" (standard deviation of step
length), "Sinuosity" (path tortuosity),
"Straightness" (straight-line efficiency),
"Velocity" (mean velocity),
"sdVelocity" (standard deviation of
velocity), "MaxVelocity" (maximum
velocity), and "MinVelocity" (minimum
velocity). This flexibility allows users to focus on specific aspects of
movement or combine multiple characteristics to create a comprehensive
profile of trackmaker behavior.
The data argument expects a
track R object and the
veltrack argument requires a
track velocity R object. These parameters
are used to enhance the clustering process by incorporating
speed-related information alongside spatial metrics.
The results of the clustering process have important biological implications. By grouping tracks with similar movement parameters, researchers can infer the behaviors that produced those tracks. For instance, tracks characterized by low sinuosity and high velocity might indicate animals moving directly toward a target, while high sinuosity and variable step lengths could suggest foraging or exploratory behavior.
Additionally, clustering can reveal coordinated movement. If multiple tracks fall within the same cluster and also exhibit high similarity when analyzed with methods like Dynamic Time Warping (DTW) or Fréchet distance, it could indicate group movement or coordinated hunting strategies.
Moreover, the clustering approach offers a practical way to refine datasets before applying more computationally demanding tests. By first identifying groups of tracks that share similar characteristics, users can focus on the most relevant comparisons, enhancing the robustness of their hypothesis testing. This pre-clustering step can significantly improve the efficiency and reliability of subsequent analyses, such as similarity metrics or intersection tests.
The output of the cluster_track()
function is a track clustering R object,
which provides detailed information about the clustering process and the
resulting classification of tracks based on their movement parameters.
The output is structured as a list containing two primary components:
matrix and
clust. The
matrix element is a data frame that holds
the calculated movement parameters for each track, including metrics
such as turning angles, step lengths, sinuosity, straightness, and
various velocity parameters. This matrix serves as the input data for
the clustering process, providing a comprehensive summary of the tracks’
movement characteristics. The clust
element is an Mclust R object generated by
the mclust package. This object contains
all the results of the model-based clustering analysis, including the
optimal model selected according to the Bayesian Information
Criterion (BIC). The clust object
includes essential information such as the number of clusters identified
(G), the specific model used
(modelName), the mixing proportions of
each component (pro), the means of each
cluster (mean), and the variance
parameters (variance). Additionally, it
provides the log-likelihood, BIC, and
ICL (Integrated Complete-data Likelihood) values
corresponding to the best-fitting model. The
classification of tracks is provided within the
clust object as the
classification element, which assigns each
track to a specific cluster. The z matrix
within this object gives the probability of each track belonging to each
cluster, while the uncertainty element
measures the confidence associated with each classification. The
cluster_track() function’s output allows
users to assess how tracks are grouped based on their movement patterns,
providing valuable insights into potential behavioral strategies. This
clustering result can be directly used to guide further analyses, such
as comparing clusters with similarity metrics or testing whether
clusters correspond to specific ecological or behavioral hypotheses.
The cluster_track() function provides a
flexible and powerful framework for identifying behavioral
patterns from trackway data, enabling researchers to draw
meaningful conclusions about the behavioral ecology of ancient
trackmakers.
Examples of Usage
First, compute velocities for the subsetted MountTom dataset using
the velocity_track() function. This object
will later be passed to
cluster_track():
H_mounttom_subset <- c(
1.380, 1.404, 1.320, 1.736, 1.432, 1.508, 1.768, 0.760, 1.688, 1.620, 1.784
)
velocity_sbmounttom <- velocity_track(sbMountTom, H = H_mounttom_subset)Next, perform clustering using key variables related to movement behavior: sinuosity, straightness, velocity, and turning angles.
clustering_mounttom <- cluster_track(
data = sbMountTom,
veltrack = velocity_sbmounttom,
variables = c("Sinuosity", "Straightness", "Velocity", "TurnAng"),
analysis = "mclust"
)#> $matrix
#> TurnAng sdTurnAng PathLen BeelineLen StLength sdStLength StrideLen
#> Track 1 136.5592 4.467360 7.082804 7.064759 0.8853504 0.05548326 1.7707009
#> Track 2 128.8950 5.148772 7.633951 7.606290 0.9542439 0.07899492 1.9084877
#> Track 3 132.4672 1.706197 4.603920 4.602306 1.1509800 0.10291723 2.3019601
#> Track 4 126.3425 4.993546 4.088891 4.077400 1.0222226 0.06773344 2.0444453
#> Track 5 119.7276 8.906416 4.870292 4.824094 0.8117153 0.11099481 1.6234307
#> Track 6 121.9937 3.409506 5.408165 5.400481 1.0816331 0.07421133 2.1632662
#> Track 7 338.1763 3.439774 4.950496 4.943628 1.2376241 0.13698500 2.4752481
#> Track 8 230.2982 10.200005 1.660380 1.640411 0.4150951 0.02811979 0.8301902
#> Track 9 116.2898 4.278817 4.140257 4.131406 1.0350641 0.05360650 2.0701283
#> Track 10 125.0358 6.748851 6.446288 6.408877 0.9208983 0.05844160 1.8417966
#> Track 11 110.6121 2.470679 4.325985 4.322800 1.0814963 0.08433082 2.1629926
#> PaceLen Sinuosity Straightness TrackWidth Gauge PaceAng
#> Track 1 0.9191016 0.11270082 0.9974524 0.1721504825 NA 158.5226
#> Track 2 0.9541748 0.09262995 0.9963766 0.0159891957 NA 173.6657
#> Track 3 1.1345215 0.03764747 0.9996494 0.0212477374 NA 174.5695
#> Track 4 1.0358257 0.10145144 0.9971898 0.0047833057 NA 172.6057
#> Track 5 0.8216841 0.12973220 0.9905143 0.0636573000 NA 166.8076
#> Track 6 1.1212537 0.07028586 0.9985792 0.1866850854 NA 161.4382
#> Track 7 1.2361499 0.05626070 0.9986127 0.0608677632 NA 175.7803
#> Track 8 0.4129860 0.27686948 0.9879729 0.0266683991 NA 163.5760
#> Track 9 1.0236417 0.08267192 0.9978623 0.0004700831 NA 171.2543
#> Track 10 0.9126663 0.08738057 0.9941965 0.1258592548 NA 170.4862
#> Track 11 1.0763069 0.05048719 0.9992637 0.1232654737 NA 164.4785
#> StepAng Velocity sdVelocity MaxVelocity MinVelocity
#> Track 1 10.626826 1.3968002 0.14439087 1.6282145 1.1263670
#> Track 2 5.892303 1.5535875 0.21607084 1.9705480 1.2282962
#> Track 3 3.035714 2.2836915 0.34151372 2.6930934 1.9459589
#> Track 4 5.141067 1.3574968 0.15085861 1.5542292 1.1964928
#> Track 5 8.342249 1.1649515 0.26140051 1.4629709 0.7937147
#> Track 6 9.462611 1.7594451 0.19822185 1.9368491 1.4623759
#> Track 7 3.718311 1.8347941 0.32941336 2.1424638 1.3785178
#> Track 8 11.268134 0.7922552 0.08889224 0.8898008 0.6789600
#> Track 9 4.587023 1.4313084 0.12214822 1.5446592 1.2579403
#> Track 10 7.654888 1.2365595 0.12945067 1.4062974 1.0226956
#> Track 11 7.244510 1.4456913 0.18479230 1.5911254 1.1928343
#>
#> $clust
#> 'Mclust' model object: (EII,9)
#>
#> Available components:
#> [1] "call" "data" "modelName" "n"
#> [5] "d" "G" "BIC" "loglik"
#> [9] "df" "bic" "icl" "hypvol"
#> [13] "parameters" "z" "classification" "uncertainty"We then check the classification of tracks.
clustering_mounttom$clust$classification#> Track 1 Track 2 Track 3 Track 4 Track 5 Track 6 Track 7 Track 8
#> 1 2 3 4 5 6 1 7
#> Track 9 Track 10 Track 11
#> 2 8 9And the probability of each track belonging to each cluster.
clustering_mounttom$clust$z#> [,1] [,2] [,3] [,4] [,5]
#> Track 1 1.000000e+00 5.221985e-35 4.860935e-153 1.239078e-86 5.808852e-89
#> Track 2 1.966107e-48 1.000000e+00 5.202275e-145 7.001205e-71 1.272419e-89
#> Track 3 3.160409e-117 4.146421e-138 1.000000e+00 1.323486e-85 2.457625e-179
#> Track 4 2.536411e-85 1.871845e-68 1.323486e-85 1.000000e+00 4.067886e-22
#> Track 5 9.153190e-101 3.965623e-92 2.457625e-179 4.067886e-22 1.000000e+00
#> Track 6 2.733824e-82 4.146387e-19 2.235701e-80 9.675740e-61 1.440681e-117
#> Track 7 1.000000e+00 1.512900e-61 1.284242e-82 3.245044e-85 9.014354e-114
#> Track 8 2.020008e-119 5.788091e-102 0.000000e+00 6.844101e-158 2.520234e-101
#> Track 9 4.018265e-48 1.000000e+00 2.065540e-132 3.127857e-67 7.724541e-96
#> Track 10 7.189284e-34 3.165595e-73 2.495518e-171 7.008780e-51 2.369398e-29
#> Track 11 1.622006e-29 1.240929e-27 1.372279e-119 1.844548e-105 4.291280e-150
#> [,6] [,7] [,8] [,9]
#> Track 1 2.312889e-83 1.818145e-73 1.019885e-23 5.329865e-24
#> Track 2 6.846217e-22 1.092173e-101 1.484236e-71 4.716941e-35
#> Track 3 2.235701e-80 0.000000e+00 2.495518e-171 1.372279e-119
#> Track 4 9.675740e-61 6.844101e-158 7.008780e-51 1.844548e-105
#> Track 5 1.440681e-117 2.520234e-101 2.369398e-29 4.291280e-150
#> Track 6 1.000000e+00 7.836224e-196 5.545566e-121 1.525733e-47
#> Track 7 2.019605e-82 1.402677e-166 3.167379e-45 3.085095e-36
#> Track 8 7.836224e-196 1.000000e+00 2.988385e-69 4.114114e-136
#> Track 9 1.569528e-17 1.917164e-103 4.219759e-76 2.040392e-21
#> Track 10 5.545566e-121 2.988385e-69 1.000000e+00 6.491022e-90
#> Track 11 1.525733e-47 4.114114e-136 6.491022e-90 1.000000e+00The resulting clusters can help infer behavioral strategies (e.g., direct vs. exploratory movement), and serve as a pre-selection step for deeper hypothesis testing. Tracks in the same cluster can be further analyzed with similarity metrics, intersection metrics, and the combined_prob() function to test whether observed movement patterns reflect non-random, coordinated, or functionally distinct behaviors—while also reducing computational cost by narrowing the scope of comparisons.
References
- Alexander, R. M. (1976). Estimates of speeds of dinosaurs. Nature, 261(5556), 129-130. DOI: https://doi.org/10.1038/261129a0.
-
Batschelet, E. (1981). Circular statistics in
biology. Academic Press, 388 pp.
- Benhamou, S. (2004). How to reliably estimate the tortuosity of an animal’s path: straightness, sinuosity, or fractal dimension?. Journal of Theoretical Biology, 229(2), 209-220. DOI: https://doi.org/10.1016/j.jtbi.2004.03.016.
-
Farlow, J. O., O’Brien, M., Kuban, G. J., Dattilo, B. F.,
Bates, K. T., Falkingham, P. L., & Piñuela, L. (2012).
Dinosaur Tracksites of the Paluxy River Valley (Glen Rose Formation,
Lower Cretaceous), Dinosaur Valley State Park, Somervell County, Texas.
In Proceedings of the V International Symposium about Dinosaur
Palaeontology and their Environment (pp. 41-69). Burgos: Salas de
los Infantes.
-
Lallensack, J. N., Leonardi, G., & Falkingham, P. L.
(2025). Glossary of tetrapod tracks. Palaeontologia
Electronica, 28(1), 1-105. DOI: https://doi.org/10.26879/1389.
-
Ostrom, J. H. (1972). Were some dinosaurs
gregarious? Palaeogeography, Palaeoclimatology, Palaeoecology,
11(4), 287-301. DOI: https://doi.org/10.1016/0031-0182(72)90049-1.
-
Rohlf, F. J. 2008. tpsUtil. Version
1.40. Department of Ecology and Evolution, State University of
New York.
Available at: https://sbmorphometrics.org/
-
Rohlf, F. J. 2009. tpsDig. Version
2.14. Department of Ecology and Evolution, State University of
New York.
Available at: https://sbmorphometrics.org/
-
Ruiz, J., & Torices, A. (2013). Humans running
at stadiums and beaches and the accuracy of speed estimations from
fossil trackways. Ichnos, 20(1), 31-35.
-
Thulborn, R. A., & Wade, M. (1984). Dinosaur
trackways in the Winton Formation (mid-Cretaceous) of Queensland.
Memoirs of the Queensland Museum, 21(2), 413-517.
- Zelditch, M., Swiderski, D., & Sheets, H. D. (2012). Geometric morphometrics for biologists: a primer. Academic Press, 477 pp.